数字控制对并网逆变器的影响及抑制方法
2016-11-05贝太周
王 萍,王 尉,贝太周,李 楠
(天津大学智能电网教育部重点实验室,天津 300072)
数字控制对并网逆变器的影响及抑制方法
王 萍,王 尉,贝太周,李 楠
(天津大学智能电网教育部重点实验室,天津 300072)
从并网逆变器控制性能的比较可知,常规的数字控制不如模拟控制.为此,以常用的准比例谐振电流控制器为例,采用传统模型、1阶惯性模型、离散化模型,分析了数字控制采样、零阶保持和滞后一拍对逆变器稳态和动态性能的影响.得出结论:数字控制使控制器和控制对象特性发生变化,系统阶数由3阶升高为4阶,相位滞后增大,开关频率及其整数倍频率出现谐振,并伴随有相位的跳变,控制参数的稳定域缩小;受稳定性的制约,稳态精度和动态性能也下降,采样频率越低时上述影响越突出.一种基于误差电流衰减的预测控制被提出用于抑制数字控制的影响.仿真和实验结果表明预测控制能减小稳态误差,动态调节时间由10,ms减少到小于5,ms,电感估计标幺值在0~1.53内变化,系统具有良好的鲁棒性.
数字控制;准比例谐振;并网逆变器;稳定域;预测控制
随着分布式发电和智能电网的快速发展,并网逆变器已经应用得越来越广泛.数字控制具有受温度影响小、易于实现复杂控制规律、调试简单、便于实现人机接口和通信等优点,尤其近年来微处理器技术性能的提升,使数字控制技术逐渐成为并网逆变器控制技术的主流.但从并网逆变器控制性能比较,常规的数字控制不如模拟控制,究其原因[1]主要有:①采样和量化过程产生的误差使系统性能有所下降,这个问题随着数字处理器硬件技术的提高,对系统性能的影响已逐渐减轻[2];②由反馈回路滤波延时、A/D转换、软件计算等带来的延时使逆变器出现最大占空比受限的问题,可以通过改进PWM脉宽调制策略[3]、滞后一拍控制[4]、预测控制[5]来解决;③零阶保持器使得控制对象的特性发生了变化[1].
数字控制对独立PWM逆变电源的影响已有研究,但未涉及到并网逆变器[6-7].文献[8]研究了数字化对单相PWM整流器的影响,指出传统的比例谐振控制器整定参数在采样频率低时,电流环不容易稳定,但没有就其原因做详细的分析.文献[1]研究了数字控制对并网逆变器稳态和动态性能的影响,选择逆变器的并网控制策略为单纯比例控制.准比例谐振(quasi-proportion resonant,Quasi-PR)控制跟踪交流量无静差,抗干扰能力强,被广泛应用于并网逆变器的控制[9].数字控制带来的最大占空比受限问题工程中通常用滞后一拍来解决[4].本文以Quasi-PR控制的通用单相并网逆变器为例,采用3种模型对比,分析采样、零阶保持、滞后一拍控制对并网逆变器性能的影响.针对数字控制尤其在采样频率较低时,Quasi-PR控制使系统的动态和稳态性能下降的情况,提出了一种预测控制的方法来解决数字控制的延时问题,通过在1,kW的单相并网逆变器平台上,对比两种控制方案10,kHz采样频率下的实验结果,验证了分析的正确性.
1 并网逆变器控制原理
通用单相并网逆变器的主电路如图1所示.

图1 并网逆变器主电路Fig.1 Main circuit of the grid-connected inverter
图中:Udc为直流母线电压;Uinv为逆变器输出电压;Io为并网电流;L为滤波电感;R为考虑电感电阻、死区、开关管导通压降等因素的阻尼电阻;Ug为电网电压;S1~S4为带续流二极管的IGBT.采用电流反馈的控制策略.现有文献对图1的并网逆变器控制建模主要有3种形式.
1.1传统模型
图2是依据传统模型对并网逆变器的控制建模.传统模型认为数字控制对逆变器的影响可以忽略不计,控制建模实际和模拟控制完全相同.图中Gc(s)为Quasi-PR电流控制器,KPWM为逆变器环节的线性等效,1/(sL+R)为滤波器的等效,D为占空比.

图2 传统模型的控制建模Fig.2 Control modeling with traditional model
1.21阶惯性模型
图3是依据1阶惯性模型对系统的控制建模.数字控制中采样周期为T,约定控制周期等于采样周期.一阶惯性模型认为,滞后一拍控制引起T的延时,零阶保持器引起平均0.5,T的延时,共计1.5,T的延时,采用KPWM/(1+1.5,Ts)来表示逆变环节,近似描述数字控制的影响.

图3 一阶惯性模型的控制建模Fig.3 Control modeling with first-order inertia model
1.3离散化模型
图4是依据离散化模型对系统的控制建模.离散化模型考虑了数字控制中采样、零阶保持和滞后一拍作用,采用z变换建立整个控制系统的离散化模型,较为精确地描述数字控制的影响.

图4 离散化模型的控制建模Fig.4 Control modeling with discrete model
2 数字控制对系统的影响
2.1数字控制对控制模型的影响
电流控制器以常用的Quasi-PR为例,图2和图3中控制器Gc(s)表达式为
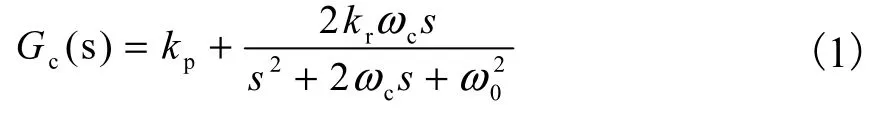
图4中Gc(z)由式(1)采用双线性变换得到.表1为不同模型建模的控制器和控制对象比较.系数ω0=100,π,rad/s,a1=4-4,ωcT+ω02T2,a2=2,ω02,T2-8,a3=4+4,ωcT+ω02,T2,b0=(44,ωcT+ω02,T2)kp-4,krωcT,b1=(2,ω02-8)kp,b2=(4+4,ωcT+ω02,T2)· kp+4,krωcT.

表1 不同模型建模的控制器和控制对象比较Tab.1 Comparison between controller and plant using different models
从表1可以看出,与传统模型比较,采用1阶惯性模型,控制器没有发生变化,控制对象从1阶变为2阶,可以证明系统的开环传递函数和闭环特征方程由3阶变为4阶.采用离散化模型,控制器由于滞后一拍的引入,从2阶变为3阶,控制对象的阶数没有发生变化,同理系统的开环传递函数和闭环特征方程由3阶变为4阶.
为了深入研究上述变化,选择参数:kp=0.1,kr= 10,ωc=5,rad/s,L=3,mH,R=0.1,Ω,T=0.000,1,s,Udc=400,V.利用Matlab做出各环节波特图.
图5是3种模型控制器的波特图.可以看出一阶惯性模型和传统模型的控制器波特图相同,从幅频特性上看,采用Quasi-PR控制,在50,Hz处控制器有20,dB的增益,带宽约为3.2,Hz,其余频率处增益接近-20,dB;从相频特性上看,频率从0增大到50,Hz相位从0°增加到78°左右,在谐振频率50,Hz处相位从78°锐减到-78°,之后随着频率的增大又逐渐回到0°.而离散化模型与上述模型幅频特性在全频段很接近,但在采样频率及其整数倍的频率上出现了谐振,且随着频率趋于无穷大,幅值不能衰减到0,dB以下;相频特性约300,Hz以下较为接近,但是由于滞后一拍存在,随着频率的增加相位滞后逐渐增大,并在采样频率及其整数倍的频率上相位出现了跳变.

图5 3种模型建模控制器波特图Fig.5 Bode diagram of controller using three models
图6是3种模型的控制对象波特图.传统模型的控制对象为一阶系统,随着频率增加,增益以-20,dB/dec递减,相位从0°逐渐减小到-90°.一阶惯性模型的控制对象,相对传统模型增加了1/(1+ 1.5,Ts)环节,在约500,Hz以下两者的幅值接近,在500,Hz以上时一阶惯性模型的幅值以-40,dB/dec递减,相位最终减小到-180°.离散化模型幅频特性在约3,800,Hz以下时与传统模型很接近,由于零阶保持器的影响,在约3,800,Hz以上时幅值不再衰减,而是在采样频率及其整数倍的频率上出现了谐振,随着频率趋于无穷大,幅值不能衰减到0,dB以下.相频特性在1,000,Hz以下时与传统模型接近,1,000,Hz以上随着频率的增加相位滞后逐渐增大,在采样频率及其整数倍的频率上相位出现了跳变.

图6 3种模型建模控制对象波特图Fig.6 Bode diagram of plant using three models
图7是3种模型建模系统开环波特图.实际上图7可由图5和图6结合而获得.传统模型幅频特性在工频处有谐振峰值,之后增益以-20,dB/dec递减.相频特性从0到50,Hz相位变化不大,在50,Hz附近相位由-10°降到-166°,之后逐渐回到-90°.1阶惯性模型在约500,Hz以下两者的幅值和相位接近,在约500,Hz以上时1阶惯性模型的幅值-40,dB/dec递减,相位最终衰减到-180°.离散化模型幅频特性在约3,800,Hz以下时与传统模型很接近,在约3,800,Hz以上时幅值不再衰减,而是在采样频率及其整数倍的频率上出现了谐振,当频率的趋于无穷大,这些谐振频率处幅值在45,dB左右.相频特性约300,Hz以下较为接近,在300,Hz随着频率的增加相位滞后逐渐增大,并在采样频率及其整数倍的频率上相位出现了跳变.

图7 3种模型建模系统开环波特图Fig.7Bode diagram of system open-loop transfer function using three models
图8是3种模型建模系统闭环波特图.3种相角裕度分别为85.9°、31.9°和-38.7°.可见传统模型也就是模拟控制时,相角裕度很大.采用一阶惯性模型近似描述数字控制影响时,相角裕度降至31.9°,说明系统的稳定性下降.采用离散化模型也就是精确模型时,相角裕度为-38.7°,可见数字控制已经使系统不稳定了,主要原因是滞后一拍、零阶保持器造成的相位滞后和采样频率及其整数倍的频率上过高的谐振.

图8 3种模型建模系统闭环波特图Fig.8 Bode diagram of system closed-loop transfer function using three models
2.2参数选择与系统稳定性的关系
下面具体分析控制参数kp、kr、ωc和采样频率f= 1/T,在3种模型建模下与系统稳定性的关系.这里考虑控制器的带宽,约定ωc=5,rad/s为定值[9].3种模型控制器分别为Gc1(s)、Gc2(s)和Gc(z),控制对象分别为Gp1(s)、Gp2(s)和Gp(z).
图9是控制器Gc2(s)随kp、kr变化的波特图.可以看出kp决定Gc2(s)全频段的增益,kr主要决定工频附近的增益.在工频附近的相位突变,kp越大,相位滞后影响的频率范围越窄,对系统的稳定越有利;反之越不利.而kr越大,相位滞后影响的频率范围越宽,对系统稳定越不利;反之越有利.
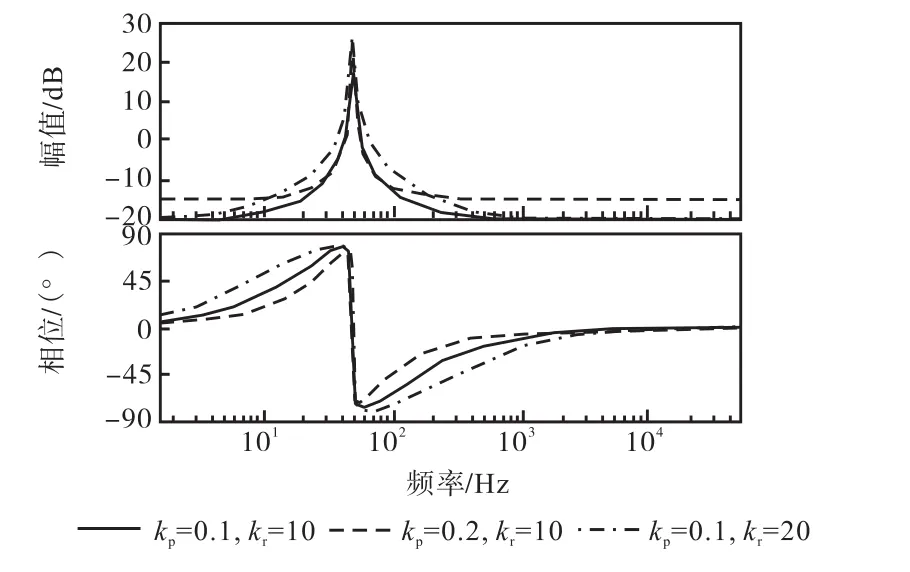
图9 kp和kr变化时Gc2(s)的波特图Fig.9 Bode diagram of Gc2(s) with kp,krchange
图10是控制器Gc(z)随kp、kr和f变化的波特图.kp和kr对Gc(z)工频附近的影响和图9的结论基本相同,但在采样频率及其整数倍的频率上的谐振由kp和kr共同决定,kp或kr越大,使这些谐振无法得到有效衰减,对系统的稳定性越不利.另外f越大,Gc(z)的相位滞后越小,谐振峰值出现越晚,对于系统越有利.
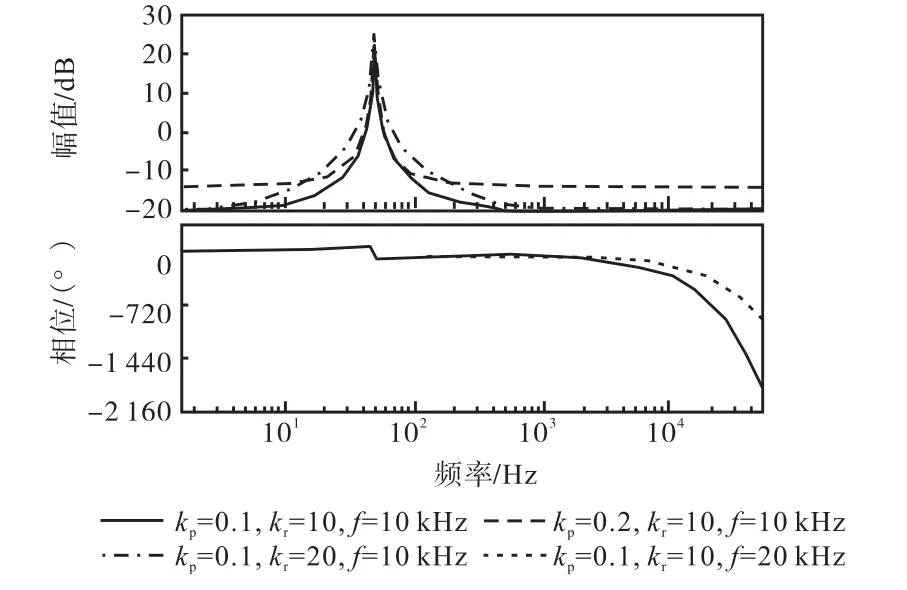
图10 kp、kr和f变化时Gc(z)的波特图Fig.10 Bode diagram of Gc(z) with kp,kr,f change
图11是控制对象Gp2(s)和Gp(z)随f变化的波特图.对于Gp2(s)来说,f越大,幅值增大,相位滞后减小对系统稳定有利.对Gp(z)来说,f越大,相位滞后越小,采样频率及其整数倍的频率上的谐振峰值出现越晚,对系统稳定越有利.

图11 f变化时Gp2(s)和Gp(z)的波特图Fig.11 Bode diagram of Gp2(s) and Gp(z) with f change
首先,对传统模型也就是模拟控制而言,由第2.1节的分析可知,控制器Gc1(s)造成的相位滞后不超过-90°,而控制对象Gp1(s)造成的相位滞后也不超过-90°,总的相位滞后不超过-180°,又因为传统模型忽略数字控制的影响,系统对任意kp、kr和f均稳定,即控制参数稳定域无限大.
对1阶惯性模型而言,结合上述关于Gc2(s)和Gp2(s)的分析,kp和f越大,kr越小,对系统稳定越有利,反之越不利.为研究kp、kr和f对稳定性的影响,先固定kr和f的值,做出闭环系统关于参数kp变化的根轨迹,进而求出kp的稳定范围.
表2是1阶惯性模型在固定kr和f的值时,使系统稳定的kp的下限值.从表2可以看出,若f为定值,当kr增大时,kp的下限值增大,原因是kr增大引起工频附近的相位滞后必须由更大的kp来弥补,才能使系统稳定;若kr为定值,f增大时,kp的下限值下降,原因在于采样频率f增大,系统的相位滞后减小,对kp补偿相位滞后的要求降低.上述结果验证了图9和图11的分析.图12是将表2中的数据利用三维做图得到的一阶惯性模型参数稳定域.稳定域为图12中平面以上的区域.
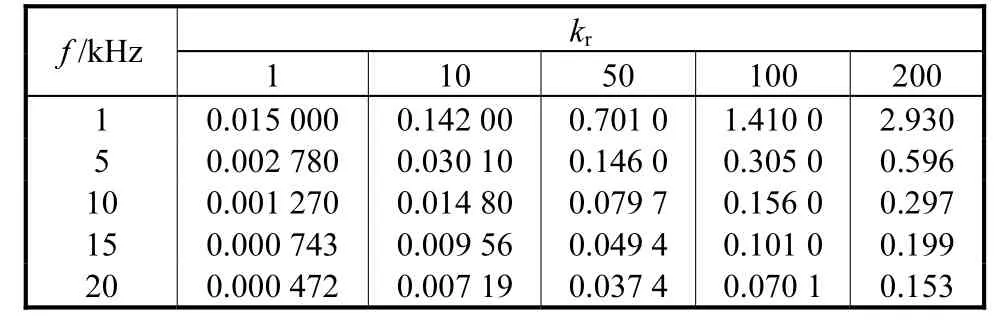
表2 一阶惯性模型参数稳定范围Tab.2 Parameter stable region using first-order inertia model

图12 1阶惯性模型参数稳定域Fig.12 Parameter stable region using one-order inertia model
对离散化模型而言,结合对Gc(z)和Gp(z)的分析,f越大,kr越小,对于系统稳定性越有利,反之越不利.kp的取值既不能过大也不能过小,否则都有可能造成系统不稳定.采取类似的方法可获得离散化模型参数的稳定范围.
表3是离散化模型在固定kr和f的值,使系统稳定的kp的取值范围.表3中“—”表示此参数下kp无论取何值系统均不稳定.当采样频率f=1,kHz时,kr在1~200范围内,由于数字控制的影响kp无论取何值系统均不能稳定.在某一参数下,kp的稳定范围既有上限值也有下限值.存在下限值是因为在工频附近,由kr引起的相位滞后必须由一定数值的kp来弥补;存在上限值是因为在采样频率及其整数倍频率上,Gc(z)和Gp(z)出现了谐振,过大的kp会使得这些谐振无法有效地衰减,造成系统高频不稳定.如表3所示,若f为定值时,kr增大,kp的稳定范围减小.下限值的增大是因为kr增大引起的工频附近的相位滞后必须由更大的kp来弥补;上限值的减小是因为kr增大引起的采样频率及其整数倍频率上Gc(z)谐振增大,必须减小kp以使得这些谐振得到有效的衰减,使系统稳定.纵向观察,kr为定值,f增大时,kp的稳定范围增大,这是因为f增大,系统的相位滞后减小,在工频附近对kp补偿相位滞后的要求降低,所以kp下限值减小;同时在采样频率及其整数倍频率上对于Gc(z)谐振幅值限制降低,所以kp上限值增大.上述结果验证了图10和图11的分析.将表3中的数据利用三维做图得到离散化模型参数稳定域,如图13所示,稳定域为图13中两平面之间的区域.
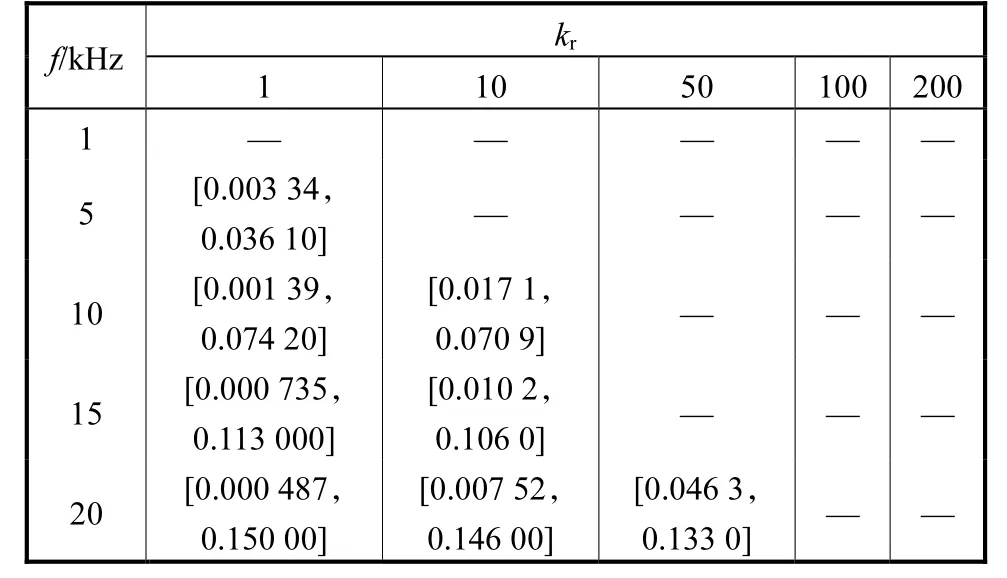
表3 离散化模型参数稳定范围Tab.3 Parameter stable region using discrete model

图13 离散化模型参数稳定域Fig.13 Parameter stable region using discrete model
2.3数字控制对逆变器稳态性能的影响
由以上分析可知,相对传统模型也就是模拟控制,数字控制中采样、零阶保持和滞后一拍,使控制器和控制对象特性发生了很大的变化,幅频特性在采样频率及其整数倍的频率上出现了谐振,相频特性的相位滞后随频率增加而增加,并且在采样频率及其整数倍的频率上出现了相位的跳变.系统的开环传递函数和闭环特征方程阶数升高,稳定裕度下降,控制参数稳定域缩小.受稳定性制约,系统开环增益减小,电流跟踪稳态误差和总谐波失真增大.采样频率越高对稳定性越有利,反之越不利.
传统模型将数字控制对系统的影响忽略不计,设计的参数可能造成系统不稳定,在采样频率越低时其可能性越大.1阶惯性模型只能近似地描述数字控制使系统在工频附近出现不稳定的情况,对系统可能出现的由于采样频率及其整数倍的频率上谐振造成的高频不稳定没有描述,所以设计的参数也可能造成系统不稳定,同样在采样频率越低时其可能性越大.
2.4数字控制对逆变器动态性能的影响
采用数字控制使控制参数的稳定域缩小,受稳定性制约,系统带宽受限制,动态性能变差.这里选择传统模型和数字控制稳定域内几组参数做出系统在f=10,kHz时的阶跃响应.图14是模拟控制和数字控制的阶跃响应.图14所示调节时间(5%误差)从上到下依次为0.55,ms、2.7,ms、1.5,ms、2.1,ms.幅值和相角稳定裕度分别为+∞和87.1°、10.6,dB和38.2°、7.0,dB和32.4°、3.0,dB和23.3°(鉴于篇幅所限,没有给出幅值和相角稳定度波特图).模拟控制的稳态和动态性能均能满足工程要求.数字控制1在保证系统基本稳定的情况下,动态性能比模拟控制差;数字控制2动态性能有所好转,但仍比模拟控制差,且稳定裕度下降了;数字控制3已经趋于不稳定,工程中不宜采用.

图14 模拟控制和数字控制的阶跃响应Fig.14 Step responses using analog and digital control
3 预测控制
由上述分析可知,数字控制对并网逆变器性能有不利影响,这种影响应在设计系统参数时具体分析.针对数字控制的影响,提出一种新的预测控制提高系统的性能.预测控制是基于离散化的控制系统模型,将当前一拍的控制量在上一拍根据预测量算出,因而能够解决数字控制带来的延时问题[5].令i= Io(t),写出系统的离散化方程为

假设i*=Io*(t)和Uinv*(t)为理想的输出电流和理想的逆变器输出电压,可得
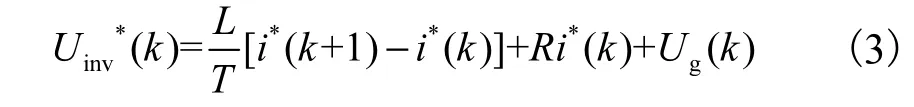
设ie=i*-i,由式(3)减式(2),忽略R项,可得

对Uinv*(k)采用一种线性预测方法进行平滑估计[10]得

笔者提出一种基于误差电流衰减的预测控制算法,电流跟踪误差每一拍以一定的比例衰减,逐渐跟踪指令电流的控制策略.设定ie(k+1)=αie(k),其中α为误差衰减因子,0≤α<1,每一拍电流误差衰减为上一拍的α.结合式(5)和式(4)得

因为ie(k)只有在第k时刻才能获得,而要计算Uinv(k)要在k-1时刻获得ie(k),因此再次采用式(5)对ie(k)进行预测,得

由此得系统控制模型如图15所示,其中T为采样周期,L*为数字控制采用的电感估计值,令kL= L*/L,为电感估计标幺值.

图15 预测控制的控制模型Fig.15 Control model using predictive control
为了确定误差衰减因子α 的最佳取值,利用阶跃响应法和根轨迹法求得的不同α 值的调节时间ts(5%误差)和系统稳定时kL的取值范围,结果如表4所示. 由表4可以看出α 越小,电流跟踪的误差衰减越快,调节时间越短,但是相应的系统稳定允许的kL的变化范围越小,即对于电感值估计误差要求越苛刻.实际中电感值随着温度和功率波动等因素变化,为了兼顾鲁棒性和快速性,最终选择α=0.5.此时系统对阶跃响应的调节时间为0.7,ms,与第2.4节模拟控制接近;与文献[11]所介绍的两种预测控制kL的稳定范围[0.81,1.25]和[0.95,1.08]相比有较大改善,与文献[10]的稳定范围[0,1.52]基本相等,对电感参数变化有较好的鲁棒性.
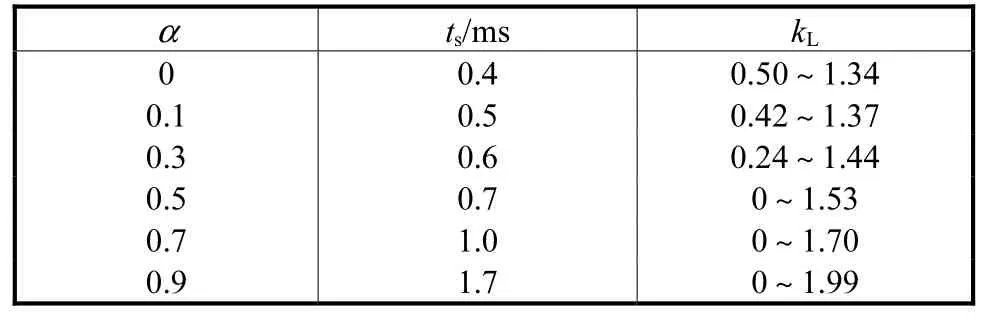
表4 不同α 值预测控制的动态响应和稳定范围Tab.4 System dynamic response and stability range under predictive control with different α
4 实验验证
为了验证本文的分析,在一个基于DSP控制的1,kW单相并网逆变器平台上,分别对基于Quasi-PR数字控制和预测控制进行了稳态和动态的实验验证.系统参数L=3,mH,R=0.1,Ω,Udc=400,V,T= 0.000,1,s.
4.1稳态实验
Quasi-PR控制参数选择kp=0.02,kr=3,ωc= 5,rad/s.预测控制α=0.5,kL=1.00.图16和图17分别为Quasi-PR控制和预测控制稳态实验波形.两种控制都能基本满足系统幅值和相位的要求.数字控制使Quasi-PR参数稳定域缩小,稳态误差和总谐波失真比预测控制的大.

图16 Quasi-PR控制稳态波形Fig.16 Steady waveforms using Quasi-PR control
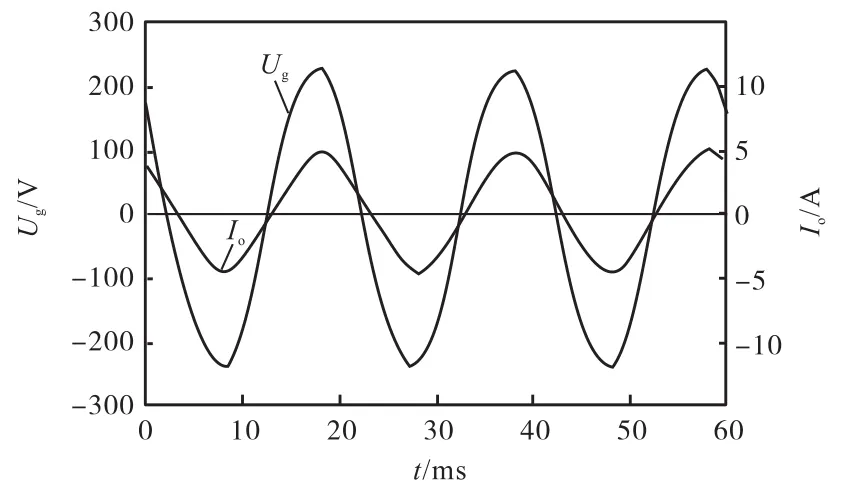
图17 预测控制稳态波形Fig.17 Steady waveforms using predictive control
4.2动态实验
图18和图19分别为Quasi-PR控制和预测控制动态实验波形.两种控制的参数与第4.1节相同.指令电流均从5,A突变为7,A.图18中数字Quasi-PR控制动态调节时间约为10,ms,因为参数的稳定域缩小,受稳定性制约,系统的带宽受到影响,跟踪电流变化性能下降.图19中α=0.5预测控制的动态调节时间小于5,ms,因为预测控制克服了数字控制的延时,当拍的控制量立刻输出,电流跟踪误差衰减较快.图18和图19动态响应时间与前文分析存在偏差,主要是因为实验中并网逆变器直流侧电压Udc不是恒定的,而分析时假定Udc恒定.

图18 Quasi-PR控制动态波形Fig.18 Dynamic waveforms using Quasi-PR control

图19 预测控制动态波形Fig.19 Dynamic waveforms using predictive control
4.3稳定实验
图20为Quasi-PR控制临界稳定波形.实验参数为kp=0.07,kr=10,ωc=5,rad/s,f=10,kHz,由表3可知这组参数接近临界稳定值.指令电流幅值为3,A.可以看出图20并网电流波形振荡剧烈,趋于不稳定.图21为预测控制临界稳定波形.控制参数为α=0.5,kL= 1.5.指令电流幅值为3,A.由表4可知这组参数也接近临界稳定值.可以看出图21并网电流波形振荡加剧,也趋于不稳定,但稳定性略好于Quasi-PR控制的情况.

图20 Quasi-PR控制临界稳定波形Fig.20 Critical stable waveforms using Quasi-PR control

图21 预测控制临界稳定波形Fig.21 Critical stable waveforms using predictive control
5 结 语
本文针对常用的Quasi-PR控制并网逆变器,以3种模型进行系统建模研究数字控制对其影响.结果表明:数字控制使系统阶数和闭环特征方程次数升高,控制器和控制对象特性发生变化,相位滞后增大,开关频率及其整数倍频率出现谐振,并伴随有相位的跳变.控制参数的稳定域缩小,系统稳定裕度下降;受系统稳定性的制约,稳态误差和总谐波失真增大,带宽受到限制,动态性能也下降.采样频率越低数字控制对系统性能的恶化越严重.依据传统模型和一阶惯性模型设计控制参数均有可能造成系统不稳定,离散化模型能较好地描述数字控制对系统影响,设计系统参数时应具体分析.本文的预测控制方法能较好地解决数字控制带来的系统性能下降的问题,理论和实验证明其具有良好的鲁棒性和动态性能.
[1] 孔雪娟. 数字控制 PWM 逆变电源关键技术研究[D].武汉:华中科技大学电气与电子工程学院,2005. Kong Xuejuan. The Key Techniques Research on the Digital Controlled PWM Inverter[D]. Wuhan:School of Electrical and Electronic Engineering,Huazhong University of Science and Technology,2005(in Chinese).
[2] 李春鹏,孙绍华. 数字控制对并网逆变系统稳定性和动态性能的影响[J]. 电力自动化设备,2012,32(3):23-27. Li Chunpeng,Sun Shaohua. Effects of digital control on stability and dynamic performance of grid connected inverter system[J].Electric Power Automation Equipment,2012,32(3):23-27(in Chinese).
[3] Deng H,Oruganti R,Srinivasan D. PWM methods to handle time delay in digital control of a UPS inverter[J]. IEEE Power Electronics Letters,2005,3(1):1-6.
[4] Basile G L,Buso S,Fasolo S,et al. A 400 Hz,100 kV·A,digitally controlled UPS for airport installations[C]//The 2000 IEEE Industry Applications Conference. Salt Lake City,USA,2000:2261-2268.
[5] 于蓉蓉,魏学业,吴小进,等. 一种改进型预测电流控制算法[J]. 电工技术学报,2010,25(7):100-107. Yu Rongrong,Wei Xueye,Wu Xiaojin,et al. An improved predictive current control algorithm[J]. Transactions of China Electro Technical Society,2010,25(7):100-107(in Chinese).
[6] 单鸿涛,彭 力,孔雪娟,等. 数字化过程对脉宽调制逆变电源性能的影响机理[J]. 中国电机工程学报,2009,29(6):29-35. Shan Hongtao,Peng Li,Kong Xuejuan,et al. Effect of digital process on the performance of pulse width modulation inverter[J]. Proceedings of the CSEE,2009,29(6):29-35(in Chinese).
[7] Mattavelli P,Polo F,Dal Lago F,et al. Analysis of control-delay reduction for the improvement of UPS voltage-loop bandwidth[J]. IEEE Transactions on Industrial Electronics,2008,55(8):2903-2911.
[8] 王 剑,郑琼林,高吉磊. 基于根轨迹法的单相PWM 整流器比例谐振电流调节器设计[J]. 电工技术学报,2012,27(9):251-256. Wang Jian,Zheng Qionglin,Gao Jilei. Design of current proportional-resonant regulator for single-phase PWM rectifier based on root-locus method[J]. Transactions of China Electro Technical Society,2012,27(9):251-256(in Chinese).
[9] 赵清林,郭小强,邬伟扬. 单相逆变器并网控制技术研究[J]. 中国电机工程学报,2007,27(16):60-64. Zhao Qinglin,Guo Xiaoqiang,Wu Weiyang. Research on control strategy for single-phase grid-connected inverter[J]. Proceedings of the CSEE,2007,27(16):60-64(in Chinese).
[10] Bode G H,Loh P C,Newman M J,et al. An improved robust predictive current regulation algorithm[J]. IEEE Transactions on Industry Applications,2005,41(6):1720-1733.
[11] Holmes D G,Martin D A. Implementation of a direct digital predictive current controller for single and three phase voltage source inverter[C]//Industry Applications Conference. San Diego,USA,1996:906-913.
(责任编辑:孙立华)
Effects of Digital Control on Grid-Connected Inverter and Its Suppression Method
Wang Ping,Wang Wei,Bei Taizhou,Li Nan
(Key Laboratory of Smart Grid of Ministry of Education,Tianjin University,Tianjin 300072,China)
When the control performance of grid-connected inverter is considered, conventional digital control is not as good as analog control. To explain this phenomenon, the commonly-used quasi proportional resonant current controller was discussed as an example. The traditional model, one order inertia model and discrete model were employed to analyze the effects of sampling, zero order holder and one-beat delay control on the steady and dynamic performance of the inverter. Conclusions are as follows: digital control changes characteristics of the controller and the plant;the order of system characteristic equation increases from 3 order to 4 order and the phase lag increases; the amplitude resonance and phase jump arise at the switching frequency and its multiple frequency; the stable region of control parameters reduces; steady-state error becomes larger and dynamic performance declines because of system stability. The above effect becomes more serious when sampling frequency gets lower. A predictive control strategy based on current-error-attenuation was proposed for suppressing effects of digital control. The simulation and experimental results show the predictive control strategy reduces the steady-state error, dynamic adjustment time decreases from 10,ms to less than 5,ms. The system is rather robust when the inductance per-unit changes from 0 to 1.53.
digital control;quasi-proportion resonant;grid-connected inverter;stable region;predictive control
TM464
A
0493-2137(2016)05-0472-08
10.11784/tdxbz201406090
2014-06-28;
2014-09-18.
高等学校博士学科点专项科研基金资助项目(20120032110070);国家国际科技合作专项项目(2013DFA11040);国家自然科学基金资助项目(61172014).
王 萍(1959—),女,博士,教授.
王 萍,pingw@tju.edu.cn.
网络出版时间:2014-11-20. 网络出版地址:http://www.cnki.net/kcms/doi/10.11784/tdxbz201406090.html.
