清晰完整话归纳

张翠萍

归纳法是从观察、实验和调查所得的个别事实中抽象概括出具有普适性的一般原理的一种思维方式或推理形式，其主要环节是归纳推理。如何才能使得归纳清晰且完整呢？笔者在教学中做了如下尝试。

一、借助直观，清晰归纳

几何直观通过图形描述和分析把复杂的数学问题变得简明、形象，在推理教学中经常会用到几何直观来明晰思路。

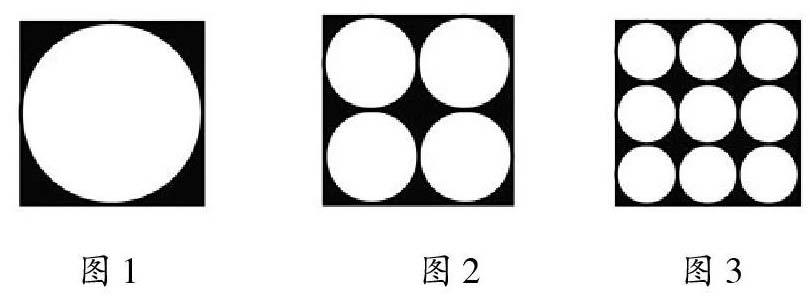
笔者在执教人教版《数学》六年级上册《圆的周长与面积计算》时，出示了这样一道思考题：有三个边长都是6厘米的正方形，第一个正方形里画1个最大的圆，第二个正方形里画4个相同的尽量大的圆，第三个正方形里画9个相同的尽量大的圆，问这几个正方形中圆的面积之和占正方形面积的百分之几？刚开始有学生猜想9个小圆的面积一定比1个大圆的面积大，也有学生反驳。笔者没有给出定论，而是引导学生先在稿纸上画出示意图，画图的过程中学生发现，要想得到面积最大的圆，圆的半径必须最长。根据题意，在第一个正方形中应画一个以正方形的中心为圆心，以正方形的边长的一半为半径的圆（如图1）。要画4个尽可能大的圆，应先将正方形分成4个等大的小正方形，再以小正方形的中心为圆心，以小正方形的边长的一半为半径画出4个等大的圆（如图2）。以此类推，要画9个等大的圆，需要先把正方形分割成9个等大的小正方形，再画出如图3所示的9个等大的圆。根据图示还无法一眼看出三幅图中圆的面积关系，不过借助图示可以知道圆的半径。通过计算，学生发现第一个正方形中大圆的面积是3.14×（6÷2）2=3.14×9，第二个正方形中四个小圆的面积之和是3.14×（6÷2÷2）2×4=3.14×9，第三个正方形中9个小圆的面积之和是3.14×（6÷3÷2）2×9=3.14×9。至此，学生发现原来这几幅图中圆的面积之和是相等的。这时有学生提出如果第四个正方形中有16个相同的尽量大的小圆，第五个正方形中有25个相同的尽量大的小圆，它们的面积之和还相等吗？笔者肯定了该学生的大胆质疑并引导全班学生共同探讨，学生们借助直观图形，再次计算验证了这一结论，并总结出依次在正方形中取n2个相同的尽量大的小圆，其面积之和相等。

以上教学中借助几何直观，学生形成了猜想，再通过计算推翻猜想，推导出了正确结论。学生通过自主探究，不断猜想、验证、反思，发现图形之间的内在联系，寻找规律，探寻本质，获得深刻理解。

二、巧妙设计，完全归纳

在小学阶段，主要学习合情推理，即归纳推理和类比推理。归纳推理又多表现为不完全归纳推理。不过，一些教学素材也可以实现完全归纳推理。教师通过巧妙的教学设计，能帮助学生建立完全归纳推理的意识。

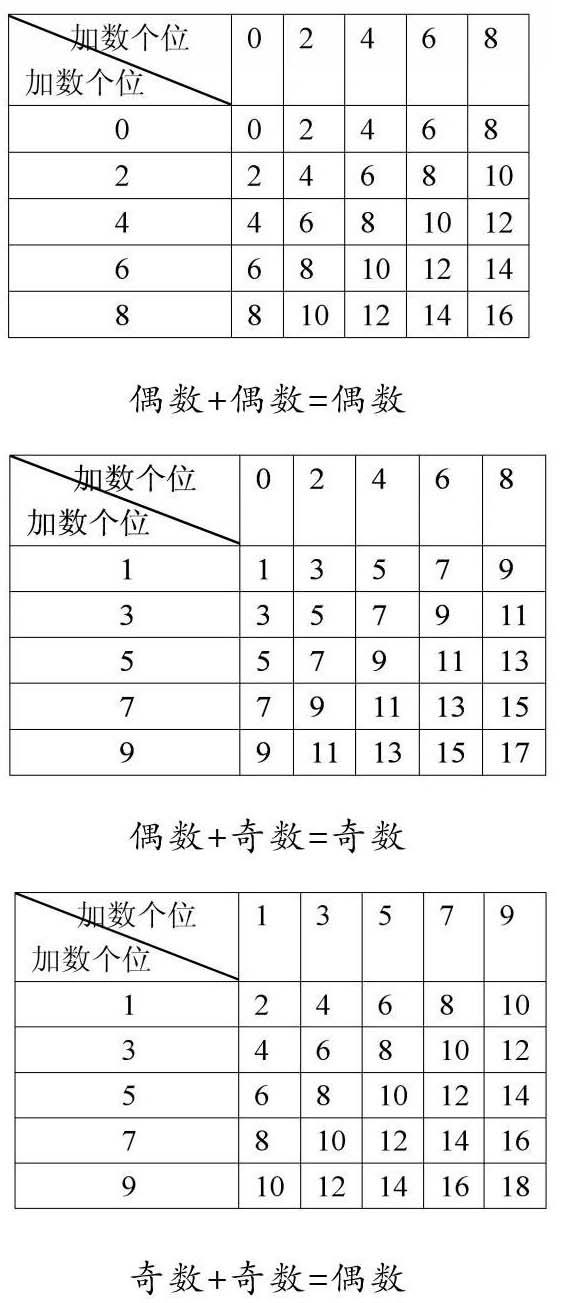
笔者借用苏教版《数学》五年级下册《和的奇偶性》的教学谈谈具体做法。课前，教师创设问题情境，与学生一起回顾一个数的奇偶性的判断定理：判断一个数是奇数还是偶数，只需要看它的个位，个位是1、3、5、7、9的数是奇数，个位是0、2、4、6、8的数是偶数。之后，又让学生判断两个数相加所得和的奇偶性，如：213214218+847645147所得的和是奇数还是偶数？学生根据它们的个位8加7等于15，推断出这两个数的和是奇数。以此为基础，笔者引导学生继续判断任意两个自然数相加所得和的奇偶性。为了便于研究，笔者先让学生将任意两个自然数相加的情况进行分类，有学生认为大致可以分为三类：偶数+偶数；奇数+奇数；偶数+奇数。这时，有学生提出，还有另外一种情况：奇数+偶数，应该是四类。正在他们僵持不下之际，有学生提出，根据加法交换律，“奇数+偶数”与“偶数+奇数”所得的和是一样的，所以还是只有三种情况。那么，它们的和又分别是奇数还是偶数呢？刚开始，学生的猜测是：偶数+偶数=偶数；奇数+奇数=奇数；偶数+奇数=奇数。如何验证呢？学生想到举例。如何举例才能穷尽所有的可能呢？由于判断一个数是奇数还是偶数只要看这个数的个位，所以只要举一位数加一位数的例子就可以了。也就是说可以用个位是0、2、4、6、8的数来代表所有的偶数，用个位是1、3、5、7、9的数来代表所有的奇数。它们相加后的所有可能可以用以下三个表格来概括。

从以上三个表格中可以清晰地看出偶数+偶数=偶数；偶数+奇数=奇数；奇数+奇数=偶数。笔者引导学生从整体入手先分类再猜想，让他们掌握了从复杂问题中找出关键要素进行有序思考的方法，从而提升了他们完全归纳推理的能力。

（作者单位：云梦县义堂中心小学）