二维旋转不变U 变换及其应用

陈伟

二维旋转不变U 变换及其应用

陈伟1

U-系统是一类L2［0，1］上的正交分段多项式函数系，为了将其推广到二维情形，传统的L2［0，1］2上张量积形式的U变换并不具有旋转不变性.本文提出了一类二维旋转不变U变换（Rotation-invariant U transform，RIUT）.RIUT将U-系统函数与调和函数相结合，使得图像的旋转转化为相位的平移而模保持不变.与经典的正交旋转不变矩（如Zernike矩）相比，RIUT具有诸多特别的性质，从而在图像特征提取中具有良好的潜力.本文将RIUT应用到二值图像检索中的实验结果表明，RIUT具有更高的检索精度.

旋转不变，U-系统，Zernike矩，二值图像检索

引用格式陈伟.二维旋转不变U变换及其应用.自动化学报，2016，42（9）：1380-1388

旋转不变性在图像目标的表达与识别中具有基本的重要性.因此，如何从图像特征中得到旋转不变量便是一个关键问题.人们已经提出了多种旋转不变特征，其中，Zernike矩［1］、伪Zernike矩［2］等旋转不变矩是一类成熟且应用十分广泛的方法.自提出以来，它们已成功应用于模式识别［3］、边缘检测［4-5］、纹理分类［6］、目标方向估计［7］等多种实际问题.

矩方法是将目标投影到一个多项式函数支撑的空间中［8］.设f（x，y）是一个分片光滑二元实值函数，其定义域为Ω⊂R×R.那么，f（x，y）的n+m阶矩定义为：

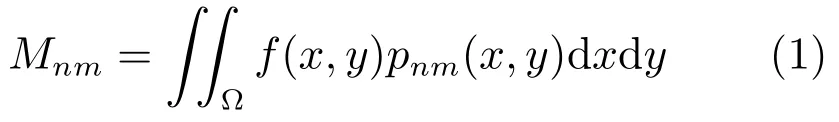
pnm（x，y）为定义域Ω上的n+m阶多项式基函数.

一般说来，式（1）中计算得到的矩值Mnm并不具有不变性.为了得到具有旋转不变性的矩函数，一种常见的方法是构造极坐标系下的复数矩.此时目标图像的旋转只会导致矩相位的变化，而矩的模值是不变的，它就是一种旋转不变量.这类矩函数的一般定义形式如下：

其中，cnm为归一化因子，（r，θ）是极坐标，Rn，m（r）为径向多项式函数，e-im为角向调和函数.

不同的径向多项式集则定义不同形式的矩.其中的Zernike多项式［1］为：

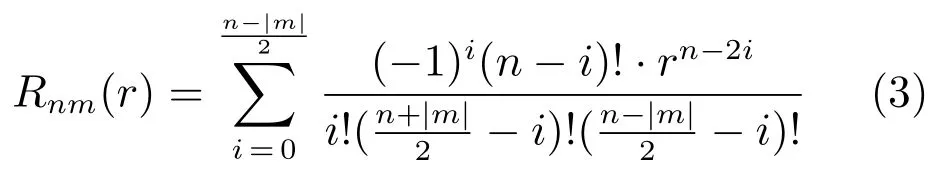
伪Zernike矩中的伪Zernike多项式［2］为：

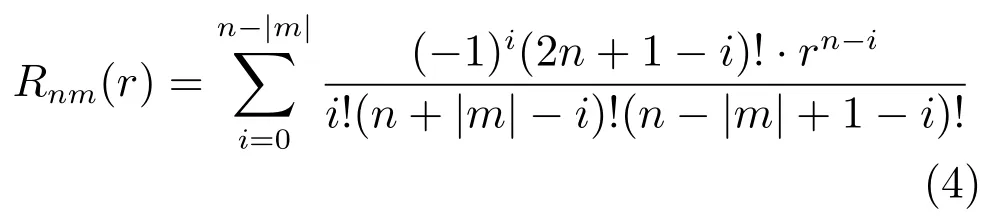
正交Fourier-Mellin矩中的径向多项式［9］为：

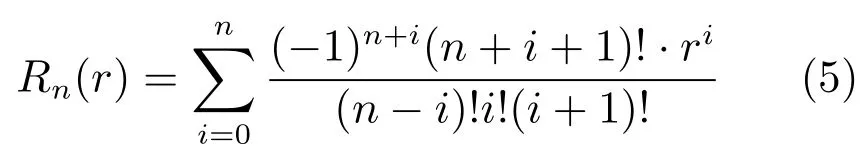
可以看出，这些多项式的表达式十分复杂，而且包含阶乘项.在实际应用中，特别是涉及高阶矩的计算时容易导致计算复杂、数值不稳定等问题［10-11］.

在本文中，我们提出一种新的二维图像变换，称为旋转不变U变换（Rotation-invariant U transform，RIUT）.RIUT具有与传统旋转不变矩相同的表达形式（式（2）），同样具有旋转不变性.但由于我们采用了一类正交分段多项式函数（U-系统）代替传统矩中的径向多项式，因此这里并没有称之为“旋转不变U矩”.

由于U-系统是一类正交分段多项式函数系，具有次数低（本文中的多项式次数仅1次）、函数结构简单的优点.U-系统有效避免了高次多项式的计算，降低了计算复杂度［12-13］.更重要的，U-系统具有诸多良好的特性，比如序率性、函数均匀支撑、连续/间断并存等，使得RIUT能够很好地捕获图像目标的特征，从而具有更好的图像特征表达能力.在本文中，我们将RIUT应用到二值图像检索中，并与经典的正交旋转不变矩，包括Zernike矩（Zernike moment，ZM）、伪Zernike矩（Pseudo-Zernike moment，PZM）及正交Fourier-Mellin矩（Orthogonal Fourier-Mellin moment，OFMM）进行比较.实验结果表明，RIUT具有更高的检索精度.

需要指出的是，虽然U-系统是一类正交函数系，但是RIUT不再是正交的，而传统的ZM、PZM及OFMM是正交的.一般说来，同时具备正交性、旋转不变性与分段低次多项式是很困难的.文献［14］尝试构造了一类同时满足这三个条件的二维变换方法，但是它的代价是径向基函数变成的形式，使得在r=0附近的计算不稳定，误差很大.本文的目的不是图像的正交重构，而是构造具有旋转不变性的二维变换，从而可以将其应用到目标识别、分类等图像不变描述中.因此，保持正交性并不是必须遵守的原则.更重要的是，U-系统具有传统正交多项式所没有的诸多特性，使得它在图像特征提取中具有一定的优势，而且二值图像检索的实验结果表明，非正交的RIUT的检索结果比传统的正交矩的结果更好.

本文的结构安排如下：第1节简要介绍U-系统的构造过程及性质；第2节介绍旋转不变U变换RIUT；第3节介绍及分析RIUT的若干性质；第4节介绍RIUT在二值图像检索中的应用，并给出实验结果；最后总结全文.

1　U-系统

1.1U-系统简介

k次（k=0，1，2，3，···）U-系统是L2［0，1］中的完备正交函数系［15-16］，它由一系列分段k次多项式组成，其中既有连续可微的多项式和k次多项式样条函数，也有函数本身及其导数各种层次间断的基函数.

1.2U-系统的构造

k次U-系统的构造过程分为3个步骤：

步骤1.取区间［0，1］上的前k+1个Legendre多项式，作为k次U-系统的前k+1个基函数，记为｛φ0（x），φ1（x），···，φk（x）｝；

1）φi（x）是以x=1/2为结点的分段k次多项式；

2）〈φi（x），φj（x）〉=δi，j，i，j∈｛0，1，2，···，k｝；

3）〈φi（x），xj〉=0，i，j∈｛0，1，2，···，k｝.

步骤3.由生成元函数迭代生成U-系统的后续函数.

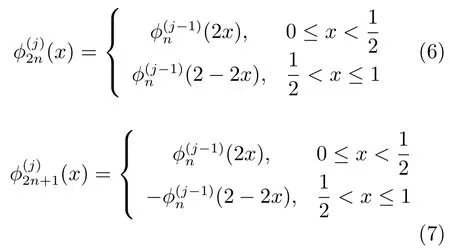
其中，n=0，1，···，（k+1）2j-1-1.在间断点处，函数值定义为两侧极限平均值.那么，函数集合

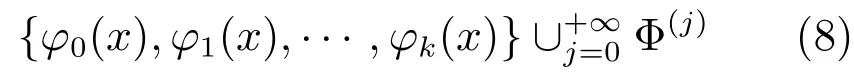
即为k次U-系统.图1显示了1次U-系统前16个基函数及其生成过程.

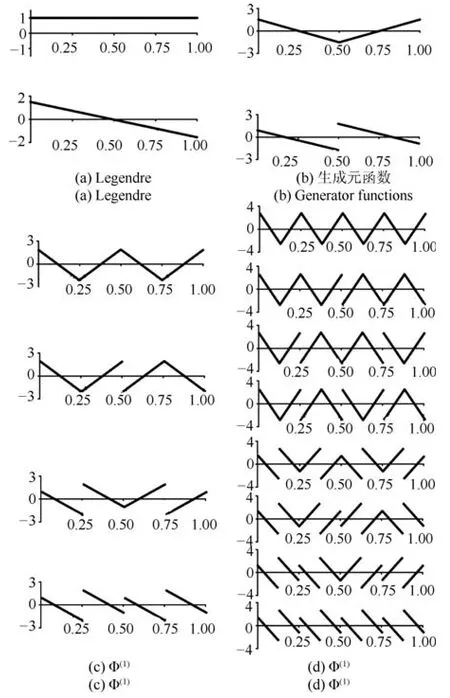
图1　1次U-系统的前16个基函数生成过程Fig.1The first sixteen basis functions in U-system of degree one

1.3U-系统的性质

在k次U-系统中，基函数按式（8）中的j值从小到大排列.记un（x）是k次U-系统的第n（n=0，1，2，···）个基函数，那么具有如下性质：

1）正交性

k次U-系统是L2［0，1］上的规范正交函数系，即〈un（x），um（x）〉=δnm.

2）收敛性

给定函数f，相应的Fourier-U级数为

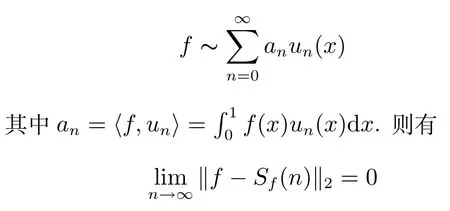
其中，Sf（n）表示Fourier-U级数的前n项部分和.

3）序率性

按式（8）给出的U-系统基函数排列次序，记为

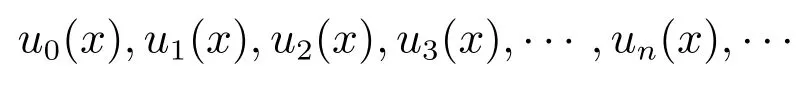
那么，当x从0到1增大，U-系统基函数的函数值符号的改变次数呈递增规律，即un（x）比un-1（x）变号恰恰多一个.

2　二维旋转不变U变换

轮廓U描述子只能提取形状的轮廓信息［17-18］，对于具有复杂结构的目标，为了提取整个区域的形状特征，则需要将U-系统推广到二维情形，得到二维区域上的U变换.

2.1L2［0，1］2上的U-系统

为了将U-系统推广到二维情形，一种直接的方法是定义L2［0，1］d（d≥2）上张量积格式的U-系统［13，18］.定义

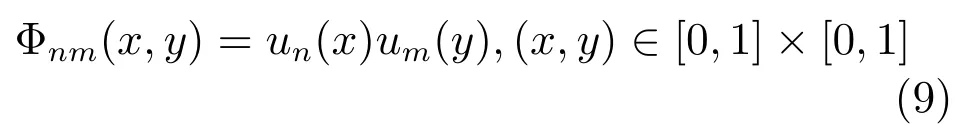
图2为当un（x），um（y）为1次U-系统基函数时Φnm（x，y）（n，m=0，1，2，···，7）的图像.由此可建立图像f（x，y）的二维U变换，如下：

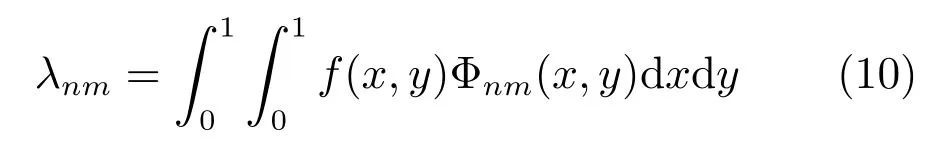
图2　L2［0，1］2上张量积形式的二维U-系统（k=1）Fig.22D tensor product U-system on L2［0，1］2（k=1）

这种二维U变换可以应用于数字图像水印［19］、图像编码［20］等领域.但是，由于它不具备旋转不变性，因而很难应用于图像形状的检索与识别.

2.2单位圆盘上的U-调和基函数

本文中，我们将U-系统函数与调和函数结合，构造了一类定义在单位圆盘上的基函数，称之为U-调和基函数.基于这种新型的二元基函数，可以方便地得到关于图像的旋转不变量.

因本文利用的是1次U-系统，记un（x）是1次U-系统的第n（n=0，1，2，···）个基函数.定义单位圆盘上的U-调和基函数为：

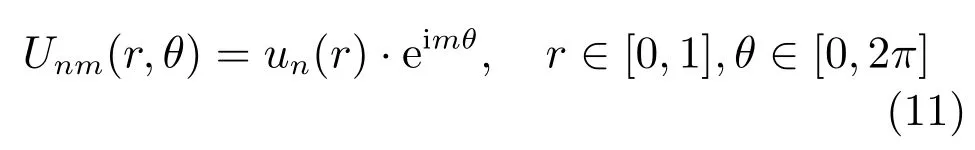
可以看出，U-调和基函数定义在整个单位圆盘上.根据式（11），这种基函数由角向函数与径向函数的乘积组成.角向为三角调和函数，径向为传统1次U-系统函数.图3显示了若干U-调和基函数的图像（均为实部）.其中，图3（a）～3（d）对应的径向基函数为u2（r），如图4（a）所示；图3（e）～3（h）对应的径向基函数为u5（r），如图4（b）所示；图3（i）～3（l）对应的径向基函数为u8（r），如图4（c）所示；图3（m）～3（p）对应的径向基函数为u10（r），如图4（d）所示.而这四组U-调和基函数的角向函数分别为eimθ，m=0，1，2，3.

图3　U-调和基函数图像Fig.3U-harmonic basis functions

2.3二维旋转不变U变换

设定义在单位圆盘上的图像f（r，θ），则它的二维旋转不变U变换为：

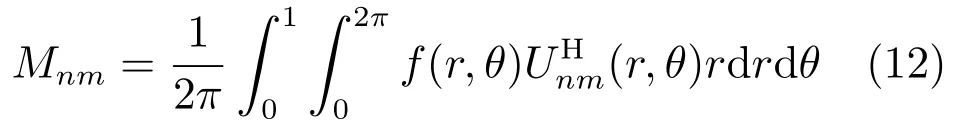
其中，［·］H表示复共轭，Mnm为图像f（r，θ）的旋转不变U变换系数，n=0，1，2，···，m= 0，±1，±2，···.

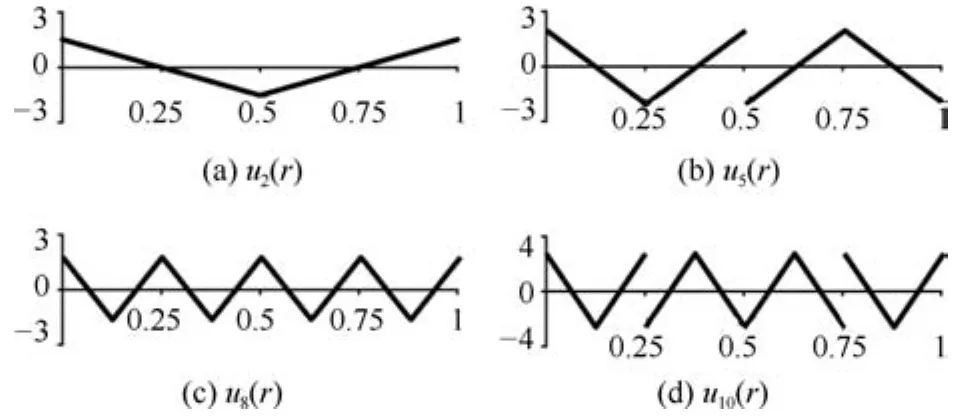
图4　U-调和基函数的径向基Fig.4The radial kernels of U-harmonic basis functions

这里需要指出的是，式（10）与式（12）分别是平面上的两种二元U-系统变换，且都是张量积形式.但两者有本质的区别，前者定义在笛卡尔坐标系下，没有旋转不变性；而后者定义在极坐标系下，很容易得到图像的旋转不变量，从而可以应用到目标识别、分类等图像不变描述的应用中.

3　旋转不变U变换的性质

本文提出的旋转不变U变换与传统的正交旋转不变矩（如Zernike矩）具有相同的表达形式，但我们采用了一类正交分段多项式函数（1次U-系统）代替传统的径向多项式，因而具有诸多特别的性质.

3.1旋转不变性

定理1（旋转不变性）.图像旋转前后，它的二维旋转不变U变换系数的模‖Mnm‖不变.

证明.设图像f（r，θ）旋转了角度φ，那么旋转后的图像f＇（r，θ）=f（r，θ+φ），则旋转后图像的U变换系数为

3.2多分辨率性

从U-系统的构造过程可知，每个U-系统基函数经“2倍压缩”与“正、反复制”，成为下一组对应U-系统基函数在［0，1/2）与（1/2，1］上的部分.因此下一组基函数的分辨率比上一组增加一倍，如此迭代下去.因此，U-调和基函数Unm（r，θ）在径向上具有多分辨率特性.另外，随着m的增大，Unm（r，θ）角向的分辨率也逐渐增加.因此，利用U-调和基函数Unm（r，θ），可以同时获得图像在径向和角向上的多分辨率特征.

3.3函数支撑

同样通过U-系统构造过程可知，每个U-系统基函数均匀地支撑在整个［0，1］区间上，幅度平稳，如图1所示.因此，当利用U-系统进行图像特征提取时，能够“均匀地”捕获图像各处的特征.

相反地，传统矩函数的径向多项式不具有这样的特性.图5（a）所示为Zernike多项式Rn，10（r）系列中的前4个多项式（n=10，12，14，16）的图像.图5（b）为局部放大图.可以看出，它们在定义域［0，1］上的分布非常不均匀，函数能量集中在区间的后半部分.需要强调的是，这不是特例，而是Zernike多项式的普遍现象.文献［21］将这种零点非均匀分布现象称为函数支撑问题.因此，在利用Zernike多项式进行图像特征提取时，容易导致非必要地刻意强调图像特定部分而抑制其他部分.

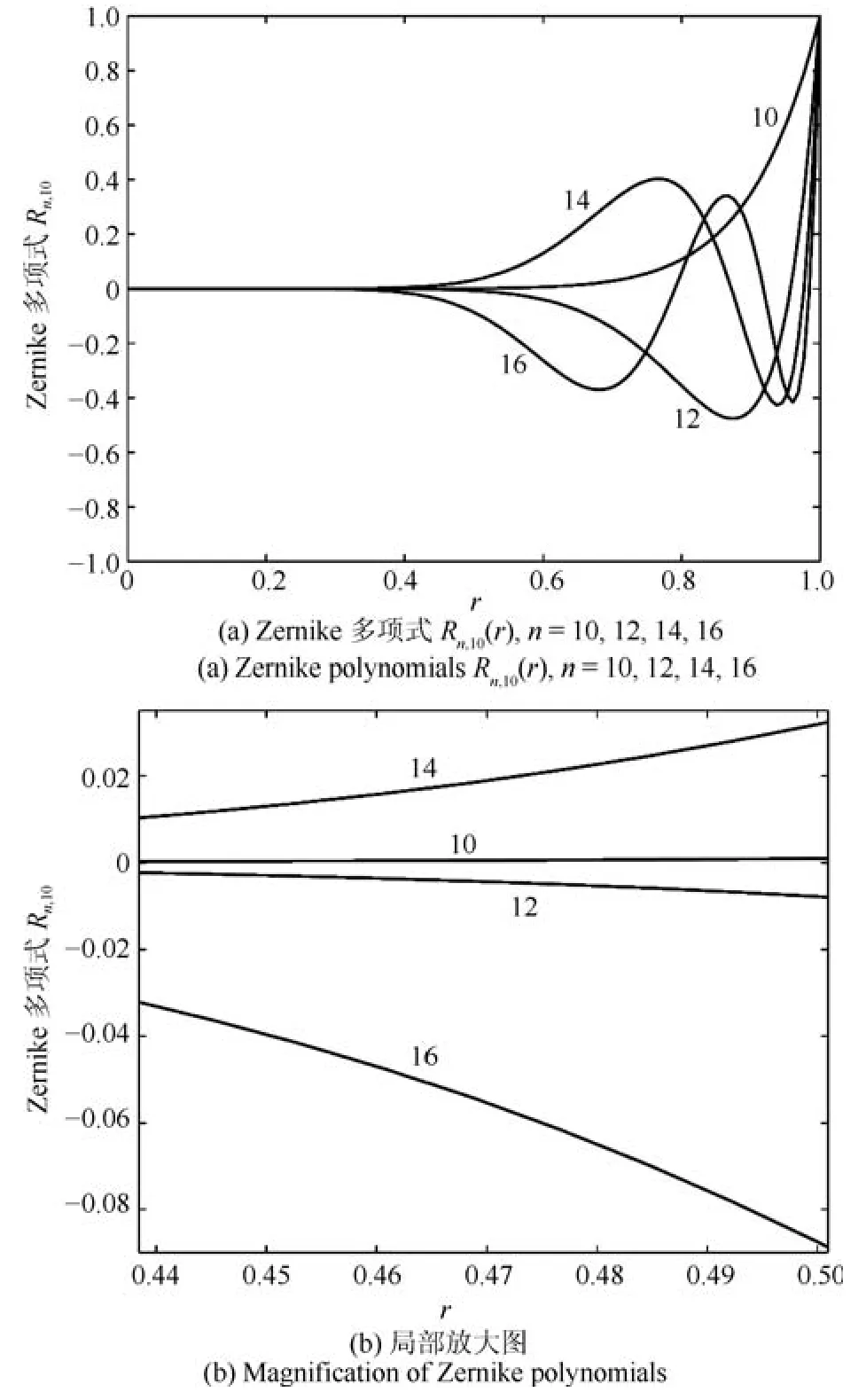
图5　Zernike多项式函数支撑Fig.5The suppression of Zernike polynomials

3.4函数零点

传统矩函数的径向多项式（比如Zernike多项式、伪Zernike多项式）的零点数目反映了函数的震荡程度.函数零点越多，震荡程度越高，越能够捕获图像的高频成份.对于n阶Zernike多项式Rnm（r），r∈［0，1］，其零点的数目为（n-|m|）/2.而对于第n个U-系统基函数un（r），r∈［0，1］，根据U-系统的序率性可知，un（r）含有n+1个零点，远多于Zernike多项式的零点.因此，当利用相同数量的变换基函数条件下，RIUT更能捕获更多的图像高频信息.

3.5间断性

如上所述，传统旋转不变矩的径向基均为多项式，具有高度光滑的特点.而本文的RIUT的径向基为U-系统，它是一类非连续的正交分段多项式函数系，其中既包含连续型的基函数，又含有大量具有各种间断性的基函数.在实际应用中，处理对象（如图像）通常是连续与间断特性并存的复杂信号，因而RIUT可以更好地表达图像的特征.

3.6离散实现

定义在单位圆盘上的旋转不变U变换针对的是连续函数.对于实际应用中的数字图像，式（12）并不能直接使用，这里给出RIUT的离散格式.

假设给定尺寸为N×N的数字图像F（i，j），1≤i，j≥N.为了计算它的U变换，需要将F（i，j）映射到函数f（xi，yj）.其中，f（xi，yj）=F（i，j），xi=（2i-N-1）/N，yi=（2j-N-1）/N，则定义在离散像素集上图像f（xi，yj）的U变换系数Mnm的计算公式为：

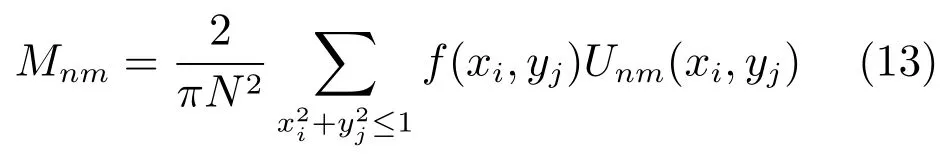
3.7RIUT描述子

在实际应用中，只有旋转不变性往往是不够的.一般来说，至少还应具有平移不变性与缩放不变性.后两种不变特征可以通过适当的图像预处理得到，从而可得到一类具有旋转（Rotation）、缩放（Scale）及平移（Translation）不变性的RIUT描述子.具体步骤如下：

假设f（x，y）为笛卡尔坐标系下的二值图像，为了得到平移不变性，将图像中形状目标的质心平移到坐标原点，作位置归一化处理即可，如下：

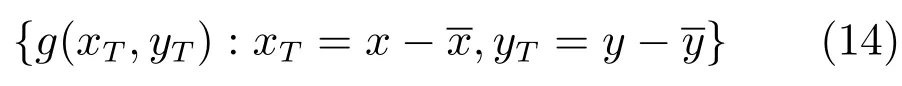
其中，g（xT，yT）为位置归一化后的图像，为原图像f（x，y）的质心，计算公式为：

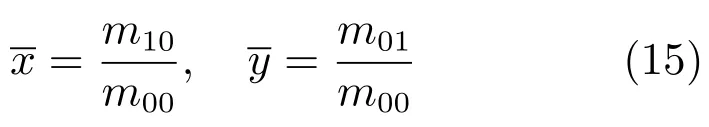
其中，m00，m10及m01为f（x，y）的几何矩.

为了得到缩放不变性，需要将图像中的形状目标尺寸进行归一化处理，如下：

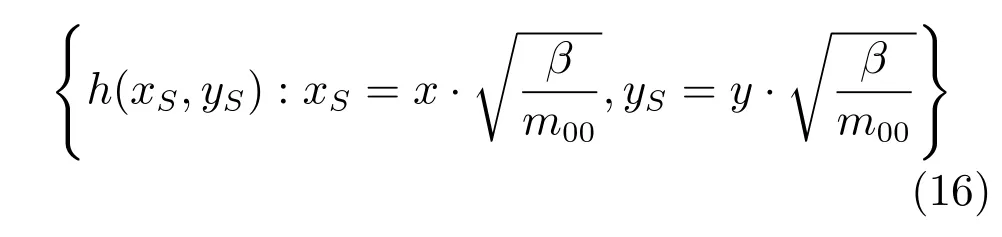
而β为预定义的形状目标的面积.

因此，图像的平移与缩放不变性可通过如下的预处理得到：

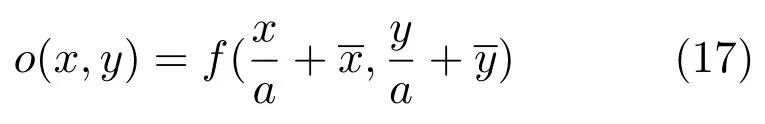
最后，对预处理后的图像o（x，y）作旋转不变U变换，得到相应的RIUT系数.将这些系数取模后得到的向量即为图像f（x，y）的RIUT描述子.图6为计算图像RIUT描述子的流程.

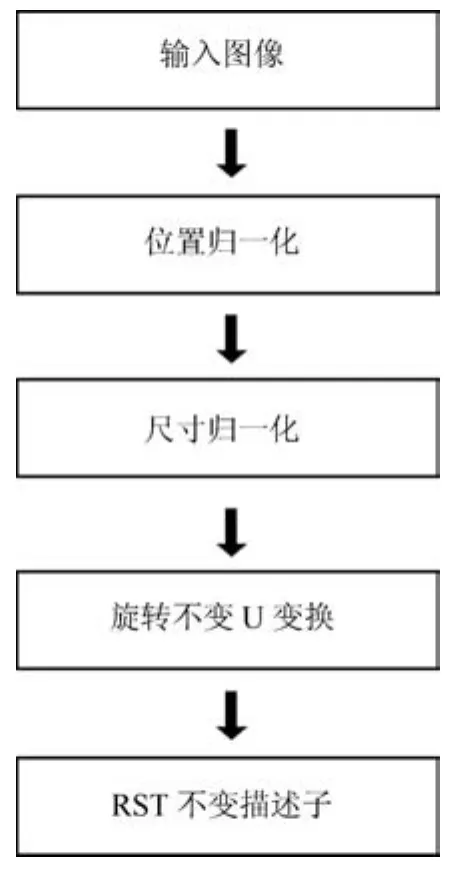
图6　图像的RIUT描述子Fig.6RIUT descriptor

4　实验

4.1旋转不变性

定理1证明了RIUT具有旋转不变性，这里将通过实验进行测试及验证.

实验1.选择一张灰度Lena图像，尺寸为128像素×128像素.因RIUT定义在单位圆盘上，因此只选择Lena图像的相应部分（即），如图7（a）所示.假设旋转了α角度（如图7（b）和7（c）），图像旋转前后的RIUT系数模分别为计算它们之间的平方误差（Mean square error，MSE），定义如下：

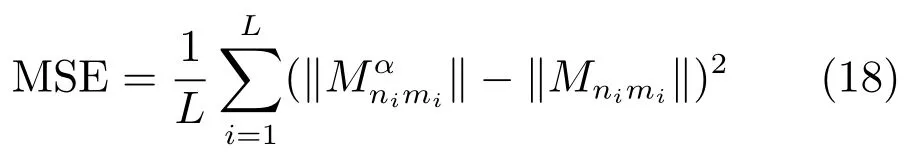
其中，L为RIUT系数的数目.本实验中，我们计算了径向函数与角向函数均为前128项的RIUT系数，共16384个.

图7　Lena图像旋转示例Fig.7Rotation examples of Lena image

我们对图7（a）从0°到90°，每间隔2.25°旋转一次，一共得到41张图像，分别计算旋转后图像与原始图像的MSE，结果如图8所示.实验结果表明，忽略因图像旋转而进行重采样引入的误差，RIUT系数模值是不变的，确实是一种旋转不变量.

图8　旋转图像的MSEFig.8The MSE of rotated images

4.2二值图像检索

构造具有旋转不变性的特征在不变模式识别中具有重要的应用价值，理论与实验结果表明，本文提出的RIUT具有良好的旋转不变性.本节我们基于RIUT描述子，将RIUT应用于二值图像检索中，并与经典的旋转不变矩方法，包括Zernike矩（ZM）、伪Zernike矩（PZM）及正交Fourier-Mellin矩（OFMM）进行比较.

在下面的实验中，我们选取标准图像检索测试集MPEG-7.该测试集包含若干图像数据库以针对不同的测试目的.RIUT与传统的旋转不变矩都是图像区域变换，因此我们选择MPEG-7测试集中的区域检索数据库CE2-A2，CE2-A4和CE2-B作为测试数据库，分别在下面的实验2至实验4中描述.

实验2.CE2-A2图像库是专门针对旋转鲁棒性检验的测试数据库.该库共包含2921张二值图像，分为21组.其中前20组是已分类图像，每组包含7张图像，由一张标准图像经不同的旋转变换得到，如图9所示.剩余未经分类的2781张图像在第21组中.

图9　CE2-A2库中图像示例Fig.9Images in CE2-A2 data set

检索精度的指标为“Bull＇s eye”算法（Bull＇s eye performance，BEP）（下同），即考虑最接近查询对象的2m个图像来计算检索正确率，这里m为每类图像中的图像数目（如本测试库中m=7）.3种矩方法采用的阶数均为8（即最高为7次多项式），RIUT则采用前8项U-系统基函数.

表1给出了本文方法RIUT及经典正交矩方法的检索精度结果.虽然这些方法在理论上都具有旋转不变性，但从实验结果可以看出，本文的RIUT方法具有更好的旋转不变鲁棒性.

表1　各方法检索精度（CE2-A2图像库）（%）Table 1Retrieval precision of different methods（CE2-A2 image data set）（%）

实验3.CE2-A4图像库包含3101张二值图像，分为31组.其中前30组是已分类图像，每组包含11张图像，由一张标准图像经不同的旋转、缩放、平移及透视变换得到，如图10所示.第31组包含2771张各不相同的未分类图像.

图10　CE2-A4库中图像示例Fig.10Images in CE2-A4 data set

表2给出了各方法的检索精度结果.从实验结果明显看出，RIUT方法优于传统的旋转不变矩方法.

表2　各方法检索精度（CE2-A4图像库）（%）Table 2Retrieval precision of different methods（CE2-A4 image data set）（%）

实验4.CE2-B图像库包含2801张不同的二值商标图像，分成11组.其中，前10组是已分类商标图像，每组中包含的相似商标数目见表3.这些商标以形状相似为分组准则，比如三角形商标、方形商标、圆形商标等，如图11所示.

表3　CE2-B库中前10组相似商标数目Table 3The similar trademarks number for the first ten groups in CE2-B data set

表4给出了每组商标的检索精度结果，其中加粗数字为每组的最高检索结果.可以看出，ZM方法与RIUT分别在4组商标中取得最高检索结果，而PZM方法在2组中取得最高结果.表5为这10组检索结果的平均值，可以看出，本文的RIUT仍取得最好结果.

表4　每组商标的检索精度（%）Table 4Retrieval precision for each group（%）

图11　CE2-B库中商标图像示例Fig.11Images in CE2-B data set

表5　平均检索精度（%）Table 5The average retrieval precision（%）

5　结论

本文基于一类正交分段多项式函数系U-系统，提出了一类新的二维旋转不变U变换RIUT.不同于以往的定义在L2［0，1］2上的二维张量积形式的U-系统，RIUT通过将U-系统函数与调和函数相结合而获得旋转不变性.RIUT有效避免了传统矩中高次多项式的计算，有效降低了计算复杂度.更重要的是，由于U-系统具有诸多良好的特性，比如序率性、函数均匀支撑、连续/间断并存等，使得RIUT在图像特征提取方面具有更多的优势.最后，在标准图像库上进行二值图像检索测试，结果表明RIUT可以得到更好的检索结果.在未来的工作中，我们将进一步分析RIUT的性质，并将其拓展到更多的实际应用中.

References

1 Teague M R.Image analysis via the general theory of moments.Journal of the Optical Society of America，1980， 70（8）：920-930

2 Teh C H，Chin R T.On image analysis by the methods of moments.IEEE Transactions on Pattern Analysis and Machine Intelligence，1988，10（4）：496-513

3 Kan C，Srinath M D.Invariant character recognition with Zernike and orthogonal Fourier-Mellin moments.Pattern Recognition，2002，35（1）：143-154

4 Ghosal S，Mehrotra R.Detection of composite edges.IEEE Transactions on Image Processing，1994，3（1）：14-25

5 Gao Shi-Yi，Zhao Ming-Yang，Zhang Lei，Zou Yuan-Yuan. Improved algorithm about subpixel edge detection of image based on Zernike orthogonal moments.Acta Automatica Sinica，2008，34（9）：1163-1168（高世一，赵明扬，张雷，邹媛媛.基于Zernike正交矩的图像亚像素边缘检测算法改进.自动化学报，2008，34（9）：1163-1168）

6 Wang L Z，Healey G.Using Zernike moments for the illumination and geometry invariant classification of multispectral texture.IEEE Transactions on Image Processing，1998，7（2）：196-203

7 Chen Z，Sun S K.A Zernike moment phase-based descriptor for local image representation and matching.IEEE Transactions on Image Processing，2010，19（1）：205-219

8 Flusser J，Suk T，Zitova B.Moments and Moment Invariants in Pattern Recognition.UK：John Wiley&Sons，2009.

9 Sheng Y L，Shen L X.Orthogonal Fourier-Mellin moments for invariant pattern recognition.Journal of the Optical Society of America A，1994，11（6）：1748-1757

10 Chong C W，Raveendran P，Mukundan R.A comparative analysis of algorithms for fast computation of Zernike moments.Pattern Recognition，2003，36（3）：731-742

11 Shu H Z，Luo L M，Coatrieux J L.Moment-based approaches in imaging part 3：computational considerations. IEEE Engineering in Medicine and Biology Magazine，2008，27（3）：89-91

12 Li Z M，Men X P，Li H.3D model retrieval based on U system rotation invariant moments.In：Proceedings of the 2nd International Conference on Pervasive Computing and Applications.Birmingham：IEEE，2007.183-188

13 Liu Yu-Jie，Li Zong-Min，Li Hua，Qi Dong-Xu.3D U system moment and 3D model retrieval.Journal of Computer-Aided Design&Computer Graphics，2006，18（8）：1111-1116（刘玉杰，李宗民，李华，齐东旭.三维U系统矩与三维模型检索.计算机辅助设计与图形学学报，2006，18（8）：1111-1116）

14 Chen Wei，Zhang Xiao-Ting.Orthogonal rotation-invariant V moments and application to image reconstruction.Acta Automatica Sinica，2015，41（2）：376-385（陈伟，张晓婷.正交旋转不变V矩及其在图像重建中的应用.自动化学报，2015，41（2）：376-385）

15 Feng Y Y，Qi D X.A sequence of piecewise orthogonal polynomials.SIAM Journal of Mathematical Analysis，1984，15：834-844

16 Qi Dong-Xu，Song Rui-Xia，Li Jian.Discontinuous Orthogonal Functions.Beijing：Scientific Press，2011.（齐东旭，宋瑞霞，李坚.非连续正交函数.北京：科学出版社，2011.）

17 Qi Dong-Xu，Tao Chen-Jun，Song Rui-Xia，Ma Hui，Sun Wei，Cai Zhan-Chuan.Representation for a group of parametric curves based on the orthogonal complete U-system. Chinese Journal of Computers，2006，29（5）：778-785（齐东旭，陶尘钧，宋瑞霞，马辉，孙伟，蔡占川.基于正交完备U-系统的参数曲线图组表达.计算机学报，2006，29（5）：778-785）

18 Cai Zhan-Chuan，Sun Wei，Qi Dong-Xu.A classification and recognition method for planar figures based on complete orthogonal U-system.Journal of Software，2006，17（Suppl.）：21-27（蔡占川，孙伟，齐东旭.基于正交完备U-系统的图形分类与识别方法.软件学报，2006，17（增刊）：21-27）

19 Ding Wei，Yan Wei-Qi，Qi Dong-Xu.Digital image watermarking based on U-system.Journal of Image and Graphics， 2001，6（6）：552-557（丁玮，闫伟齐，齐东旭.基于U系统的数字图象水印技术.中国图象图形学报，2001，6（6）：552-557）

20 Xiong Gang-Qiang，Yu Jian-De，Xiong Chang-Zhen，Qi Dong-Xu.Reversible factorization of U orthogonal transform and image lossless coding.Journal of Computer Research and Development，2012，49（4）：856-863（熊刚强，余建德，熊昌镇，齐东旭.U-正交变换的可逆实现及其图像无损编码.计算机研究与发展，2012，49（4）：856-863）

21 Abu-Mostafa Y S，Psaltis D.Recognitive aspects of moment invariants.IEEE Transactions on Pattern Analysis and Machine Intelligence，1984，6（6）：698-706

陈伟江南大学数字媒体学院讲师. 2013年获得澳门科技大学理学博士学位.主要研究方向为计算机图形学和图像处理.

E-mail：wchen_jdsm@163.com

（CHEN WeiLecturer at the School of Digital Medial，Jiangnan University.He received his Ph.D.degree from Macau University of Science and Technology in 2013.His research interest covers computer graphics and image processing.）

2D Rotation-invariant U Transform and Its Application

CHEN Wei1

U-system is a class of orthogonal piecewise-polynomial function system in L2［0，1］，and its generalized U-system in L2［0，1］2with tensor-product form is not rotation-invariant.In this paper，we present a novel 2D transform named rotation-invariant U transform（RIUT）.The construction of RIUT combines U-system functions with harmonic functions so that the object＇s rotation is transformed into its phase＇s translation and the modulus keeps unchanged. Compared with the classical rotation-invariant moments，such as Zernike moment，RIUT has many special properties，suggesting an applying potential in image feature extraction.The experiment results for binary image retrieval show that RIUT method has a higher retrieval precision.

Rotation-invariant，U-system，Zernike moment，binary image retrieval

Manuscript October 12，2015；accepted March 10，2016

10.16383/j.aas.2016.c150630

Chen Wei.2D rotation-invariant U transform and its application.Acta Automatica Sinica，2016，42（9）：1380-1388

2015-10-12录用日期2016-03-10

国家自然科学基金（61602213，61170320，61402201），浙江大学CAD&CG国家重点实验室开放课题（A1609），中央高校基本科研业务费专项资金（JUSRP11416），国家科技支撑计划（2015BAH54F00）资助

Supported by National Natural Science Foundation of China（61602213，61170320，61402201），the Open Project Program of the State Key Laboratory of CAD&CG of Zhejiang University（A1609），Fundamental Research Funds for the Central Universities of China（JUSRP11416），and National Science and Technology Support Program（2015BAH54F00）

本文责任编委黄庆明

Recommended by Associate Editor HUANG Qing-Ming

1.江南大学数字媒体学院无锡214122

1.School of Digital Media，Jiangnan University，Wuxi 214122