全变差图像恢复的自适应步长梯度投影算法

张本鑫　朱志斌

全变差图像恢复的自适应步长梯度投影算法

张本鑫1，2朱志斌3，4

针对图像去噪问题，本文基于全变差对偶公式提出一个新的梯度投影算法.算法采用改进的非单调线搜索和自适应BB（Barzilai-Borwein）步长，有效地改善了Chambolle梯度投影算法收敛慢的缺点.数值结果表明新算法优于一些已有的梯度投影算法.

梯度投影，全变差，自适应步长，改进的线搜索，图像恢复

引用格式张本鑫，朱志斌.全变差图像恢复的自适应步长梯度投影算法.自动化学报，2016，42（9）：1347-1355

自从Rudin，Osher和Fatemi（ROF）第一次提出全变差（Total variation，TV）去噪模型［1］，TV模型已经成为图像处理领域中非常成功的技术，在图像恢复、去模糊、重建、修复等［2-5］方面得到广泛应用.ROF模型可以保留图像的不连续边界同时用下面的最小化函数去除噪音：

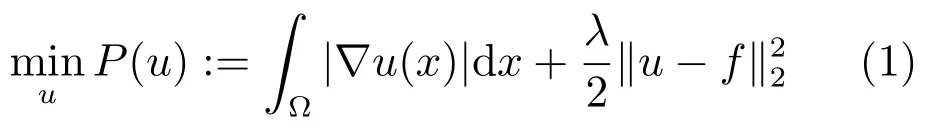
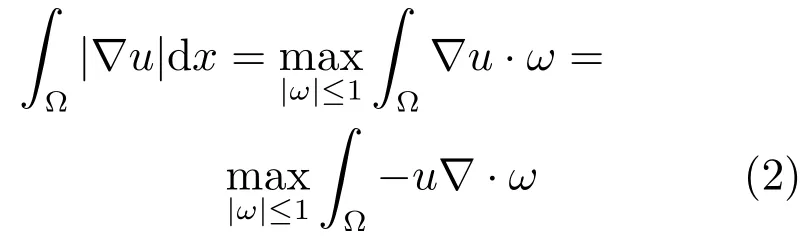
其中ω：Ω→R2是对偶变量.∇·是散度算子.最近许多学者提出一些关于对偶ROF公式的算法.由于在对偶的情况下，不需要进行光滑化处理.因此可以直接得到原问题的最优解.Chan等提出对偶的想法［6］，并用牛顿法求解对偶形式的ROF模型.因此他们的方法具有局部二次收敛速度.但算法需要计算矩阵的逆.Chambolle提出了梯度投影下降算法［7-8］，它能快速收敛于中等精度而被广泛应用.随后许多学者提出了基于Chambolle全变差最小化算法.基于二阶广义全变差正则项，文献［9］提出了模糊图像恢复的分裂Bregman算法.二阶全变差可能需要较多的计算这会导致算法的CPU时间增多.文献［10］提出了一个结合BB（Barzilai-Borwein）步长的谱共轭梯度投影算法求解图像去噪问题，该算法使用了单调线搜索，这可能会限制BB步长的数值表现.Xiao等提出了一个求解l1非光滑问题的非单调BB梯度算法［11］，数值结果表明可以和比较著名的算法相媲美.文献［12-13］将交替使用BB步长的投影梯度算法应用到压缩感知和非负矩阵的分解上，并取得了较好的效果.文献［14］在子算法中结合BB步长，有效地求解了核范数极小化问题.文献［15］提出了求解全变差图像恢复问题的非单调梯度投影算法.将Chambolle的最小化全变差方法拓展到非单调下降方法，先用BB步长代替Chambolle投影算法的常数步长，再用Dai等提出的自适应非单调线搜索［16］保证算法的全局收敛性.

在高精度要求时，数值试验表明，交替使用BB步长比单独使用某一个BB公式的效果更好.因此，本文提出了一个基于全变差图像恢复自适应步长选择的BB梯度投影算法.为了保证算法的收敛性，给出一个修正的非单调线搜索.这个线搜索可以得到一个较大的步长以及较少的计算函数值次数，因而减少算法迭代的时间.

1　自适应BB步长投影算法

Chambolle在文献［7］中得到问题（1）的解u表示如下：

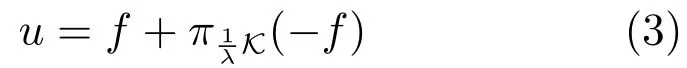
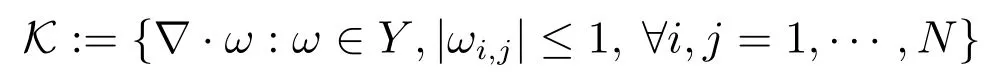
上式中散度算子∇·：X→Y定义为∇·=-∇∗，即对任意的ω∈Y和u∈X，〈-∇·ω，u〉=〈ω，∇u〉.因此求取式（1）的解取决于计算非线性映射，即等价于求解下面的约束优化问题：

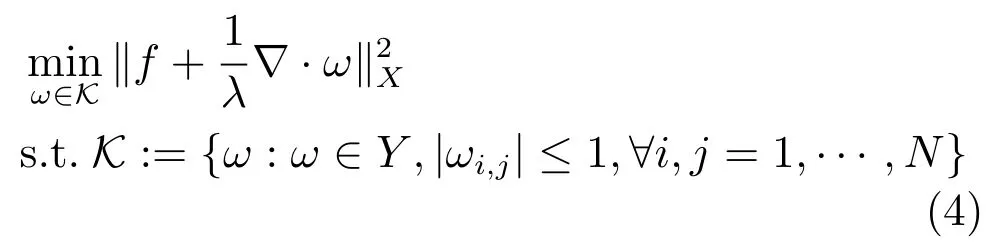
对偶问题（4）的KKT（Karush-Kuhn-Tucker）条件为：

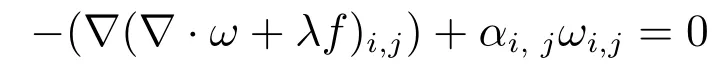
其中当|ωi，j|=1时，αi，j＞0.当|ωi，j|＜1时，αi，j=0.在后一种情况下，（∇（∇·ω+λf））i，j=0.故，综合可知拉格朗日乘子α∈X满足

由上述分析可知问题（4）的欧拉—拉格朗日公式为

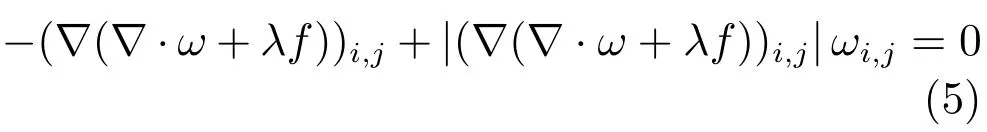
因此，Chambolle提出了一个半隐式梯度下降算法：

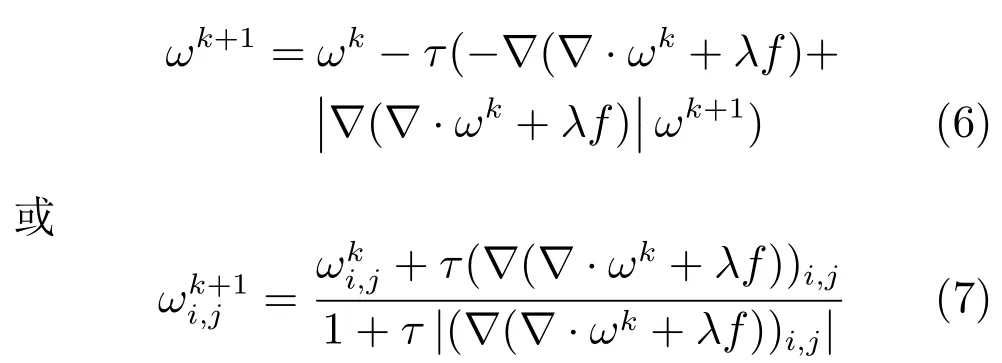
其中τ＞0是一个时间步长.显然，在Chambolle的投影算法中只要初始条件满足|ω|≤1，那么在迭代过程中ω自然满足约束条件.为了保证算法（7）的收敛性，Chambolle给出了下面的充分条件.

在文献［8］中，Chambolle建议用一个简单的投影梯度下降方法代替式（7），即

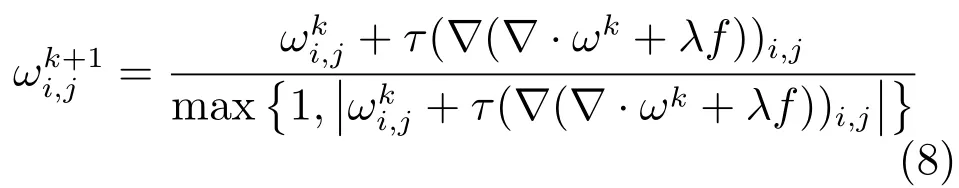
应用梯度投影算法的基本结果，文献［17］证明了当0＜τ≤1/4时，式（8）是收敛的.试验表明当τ=0.248时会有更好的数值表现.不管是半隐式梯度下降算法（7）还是梯度投影算法（8）都需要函数值在每次迭代时单调下降.但当目标函数病态时，收敛到最优值的速度常常会变慢.这可以解释为用最速下降法求解无约束优化问题，初始的几步收敛得比较快，这是为什么Chambolle梯度投影算法能快速地收敛于中等精度的原因.但当接近于最优解时，算法会出现“锯齿”现象，导致收敛速度变慢.采用BB步长可以有效地解决上述问题.特别是对于二次函数，在问题病态时，交替使用BB步长会克服问题的病态性，更快地收敛于最优解，详细分析见文献［18］.许多文献表明，在高精度要求时采用自适应BB步长会有更好的数值表现，本文数值试验部分也验证了这一点.

本节提出一个求解问题（4）的非单调自适应步长梯度投影算法，它有效地改进上述算法中式（7）和（8）收敛慢的缺点.问题（4）可以看作是在闭凸集上求解一个可微凸函数的最小化问题.首先考虑无约束优化问题minω∈RnF（ω），梯度方法的迭代过程为ωk+1=ωk-µkgk，k=0，1，···，gk=∇F（ωk），其中步长µk＞0通过合适的选择规则确定.

Barzilai等提出一个独创性的梯度方法［19］，步长由下面两式决定：

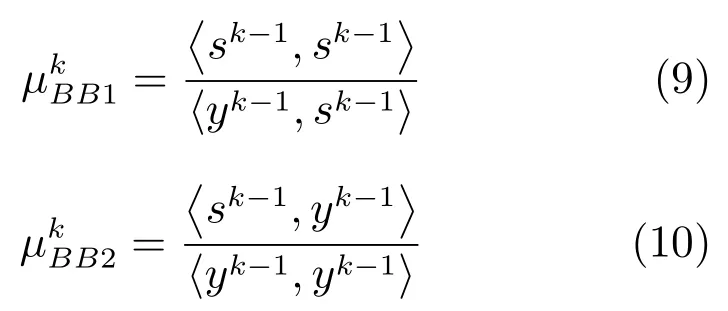
其中sk-1=ωk-ωk-1，yk-1=gk-gk-1.实际上，是以下两个近似割线方程

的最优解.它是投影拟牛顿法的一种快速逼近算法.由于其形式简单以及数值表现突出，故在工程应用中得到了极大的关注.

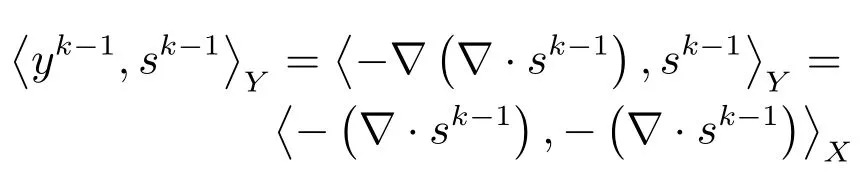
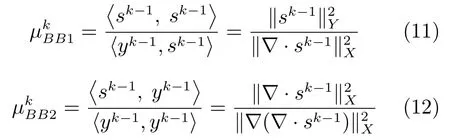
用式（11）和（12）代替Chambolle算法中的时间步长τ，得到两个相应的非单调Chambolle投影算法.即非单调Chambolle半隐式梯度投影算法：

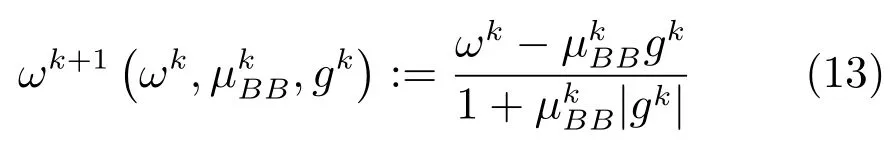
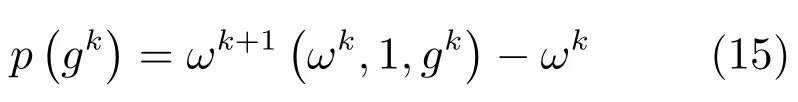
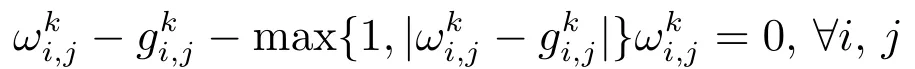
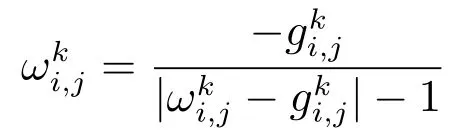
下面给出改进的非单调线搜索梯度投影算法的具体步骤，记为算法1.

算法1.改进的非单调线搜索梯度投影算法

少先队员们在志愿活动中自主策划方案、自主践行活动、自主评价成果，不断促进自身主动地成长。自主，是少先队员当家做主的权利，是雏鹰日渐丰满羽翼的催化剂，是少先队员翱翔蓝天的力量源泉！

步骤1.给定ω0∈Y，M≥1，θ∈（0，1），∈∈（0，1），k：=0，0＜ρmin＜ρmax.

步骤2.如果‖p（gk）‖=0，停止.

步骤5.改进的非单调线搜索：

步骤6.令k=k+1，转步骤2.

步骤3中的自适应BB步长选择算法：

步骤3.1.若k=0，令µ0∈［ρmin，ρmax］，τ1∈（0，1），Mµ为一正整数.

3.6，否则转步骤3.3.

步骤3.3.求

定义gs（ω）=ω（ω，µBB，g）-ω，其中s∈［ρmin，ρmax］.由文献［20］中的引理2.1可知，

如果ωk不是稳定点，那么〈gk，dk〉＜-‖dk‖2/ρmax，因此搜索方向是下降方向.如果γ=0，式（16）就是标准的非单调线搜索.再由文献［20］中的定理2.3知，只要∈［ρmin，ρmax］，算法1是收敛的.下面给出一般情形下算法1的收敛性.

定理2.算法1是适定的，且序列｛ωk｝的任意聚点ω∗是式（4）的约束稳定点.

再由γ的取值可得

所以式（16）是非单调下降，步长可以有限步得到.因此，算法1是适定的.

令ω∗是｛ωk｝的聚点.考虑下面两种情况：

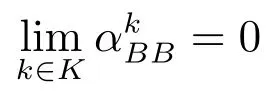
剩下的证明类似于文献［20］中定理2.3，此处不再详细给出，有兴趣的读者可以参考文献［20］.因此，ω∗是一个约束稳定点.

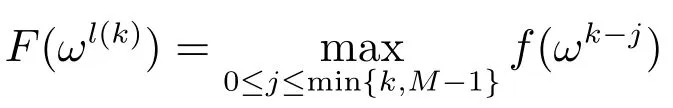
成立的整数.再由式（16）可得，对于k＞M-1（见文献［21］），

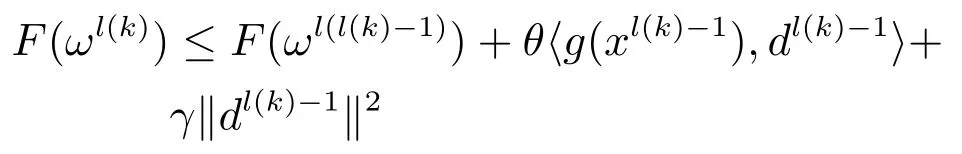
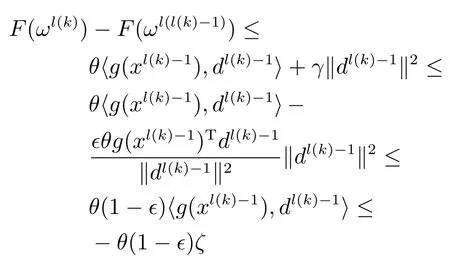
当k→∞时，F（ωl（k））→-∞，与F（ω）有界矛盾.因此，ω∗是一个约束稳定点.⁄

定理3是文献［22］中的命题1，该性质说明由对偶问题的解可以得到原问题的解.

定理3.令｛ωk｝是任意的序列，ωk∈K，k= 1，2，···，K=｛ω：|ω|≤1｝且｛ωk｝的所有聚点是式（4）的稳定点.那么当k→∞时，序列收敛于式（1）的唯一解

2　数值结果

本节给出算法1的数值表现.仿真实验在内存为2GB处理器为i3的个人电脑上进行.在两个实验中，Matlab版本为R2011a，高斯噪音由Matlab中的加噪函数imnoise产生，方差是0.01.采用均方根误差（Root mean square error，RMSE）评价算法恢复的效果，定义如下

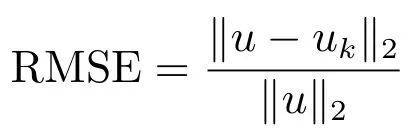
其中u是真实的图像，uk是算法得到的图像.

2.1和Chambolle梯度投影算法比较

本节将算法1和文献［7—8］中的方法进行对比.在算法1中，参数设置如下，α0=1，M=5，θ=10-5，ρmax=1010，ρmin=10-10，σ=0.5.保真项λ=0.053.

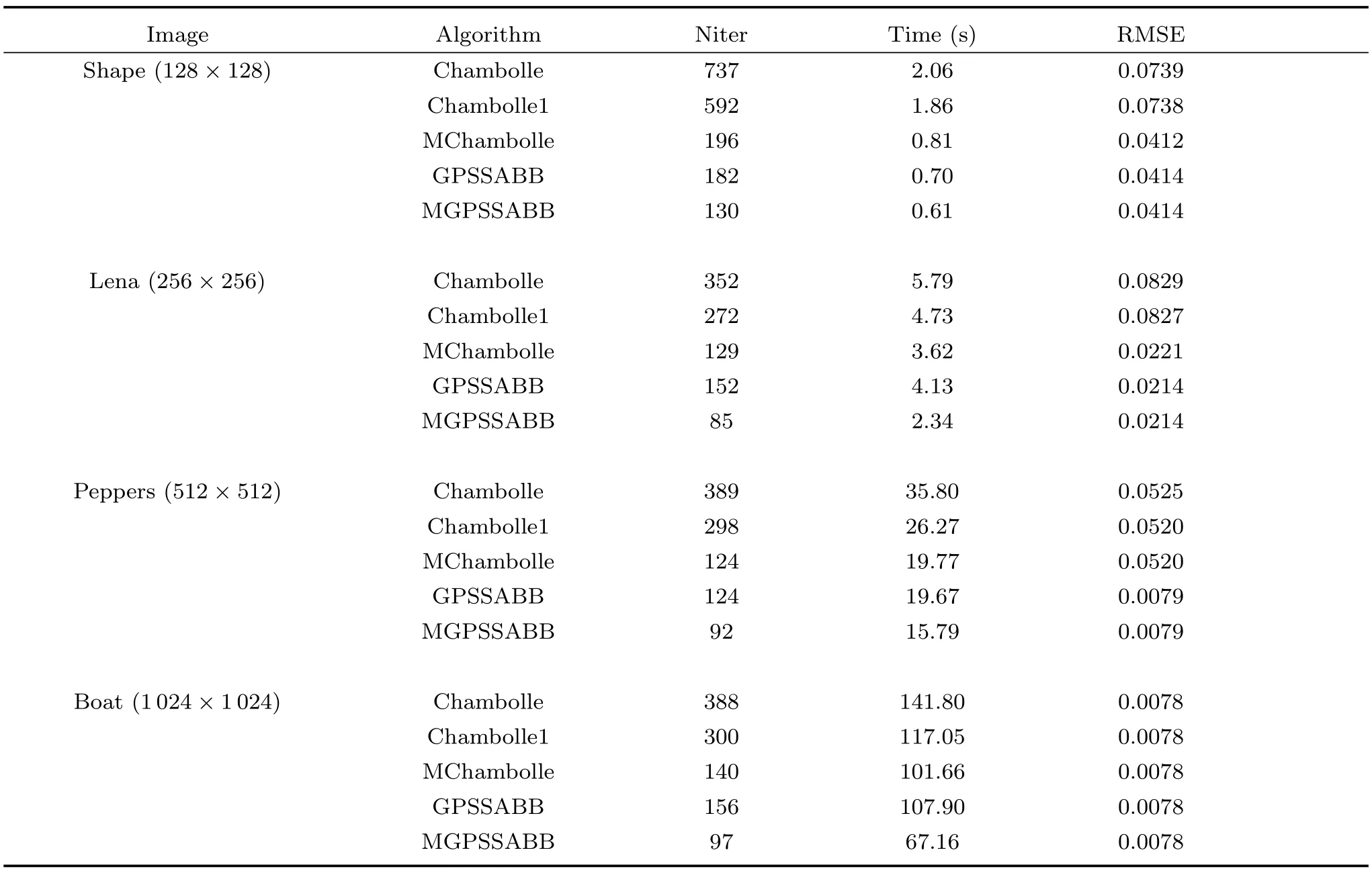
表1　数值结果Table 1Numerical results

测试如下算法：

1）文献［7］算法：半隐式梯度下降算法，τ= 0.248，记为Chambolle.

2）文献［8］算法：梯度投影下降算法，τ= 0.248，记为Chambolle1.

3）MChambolle：算法1中自适应步长选择算法，ωk+1（·）由式（13）计算，γ=0.5.

4）GPSSABB：算法1中自适应步长选择算法，ωk+1（·）由式（14）计算，γ=0.

5）MGPSSABB：算法1中自适应步长选择算法，ωk+1（·）由式（14）计算，γ=0.5.五种方法的停止准则为

为了公平测试算法的速率，每幅图像进行10次试验，表1给出迭代步数和CPU时间（秒）的10次平均数值结果.可以看出，四种方法恢复的RMSE值相差不大，但算法1有效地改善了Chambolle算法的收敛速度.图1给出了Boat（1024×1024）恢复的结果.图2说明非单调下降算法有效地改善原始算法的数值表现，特别是对高精度要求和大尺寸的图像效果更好.

图1　Boat（1024×1024）去噪结果Fig.1Denoising results of Boat（1024×1024）

2.2和梯度投影类算法比较

文献［22］给出求解式（4）的一系列BB梯度投影算法且在基于对偶间隙的基础上给出算法的一个停止准则.下面给出文献［22］中基于对偶间隙的停止准则.

由TV范数的定义，ROF模型有如下形式：

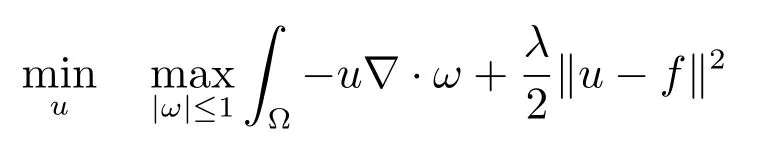
利用文献［23］中命题2.4的min-max定理，问题（1）可转化为：

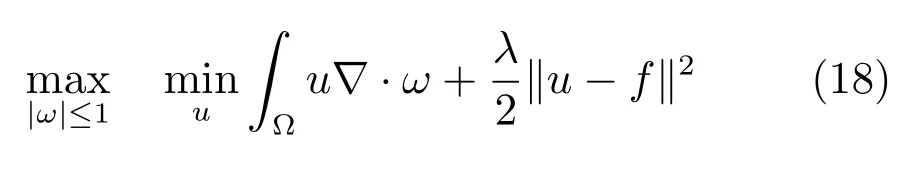
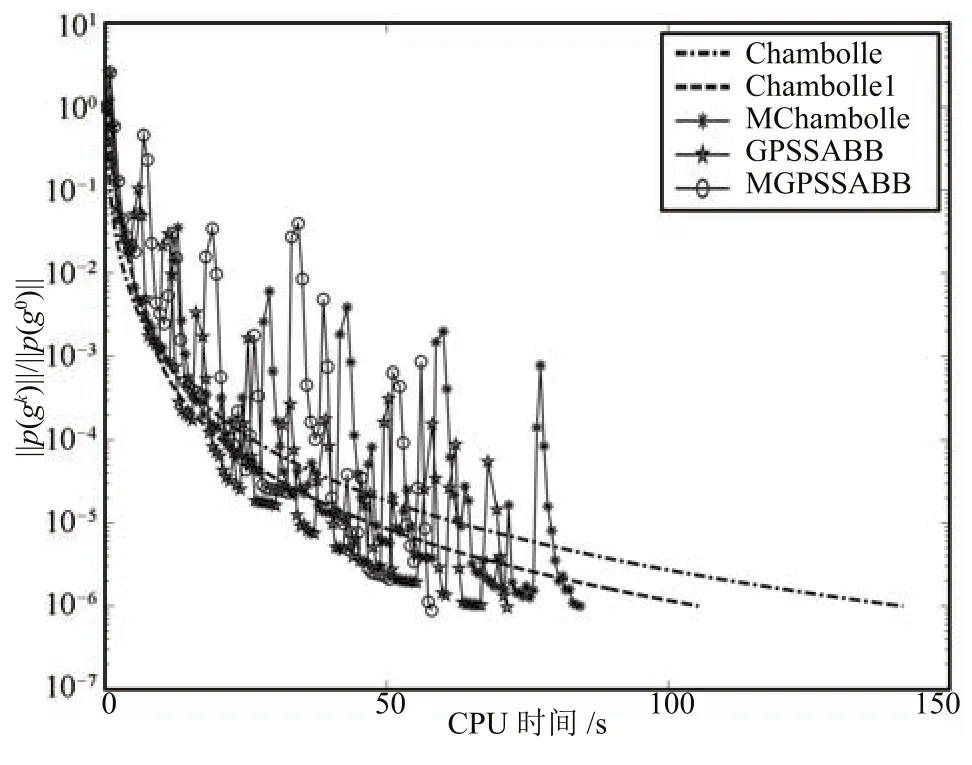
图2　Boat（1024×1024）梯度投影的相对范数vs.CPU时间（秒）Fig.2Relative norm of projected gradient vs. CPU time（s）of Boat（1024×1024）

式（18）中内层最小化问题的精确解为：

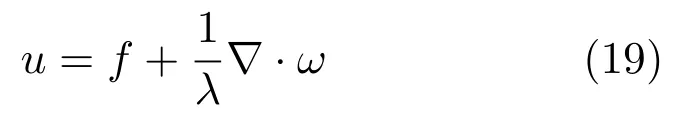
将式（19）代入式（18）中，可得对偶问题：

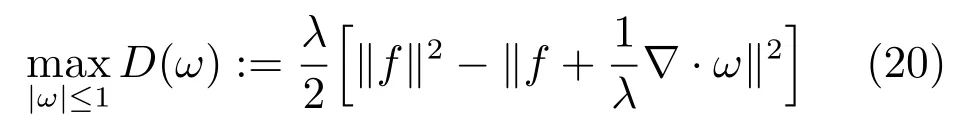
对偶间隙定义如下：

如果u和ω是可行解，那么

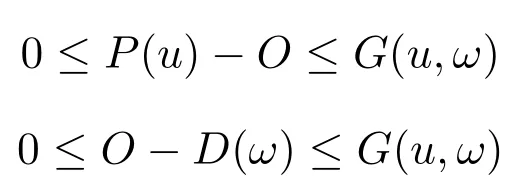
其中O为原对偶最优值.如果（u，ω）是原对偶问题的最优解，那么

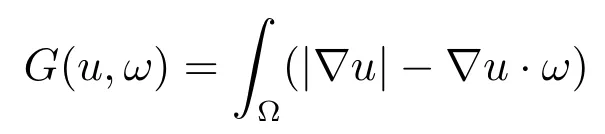
下面具体分析当ω=ωk满足如下停止准则时

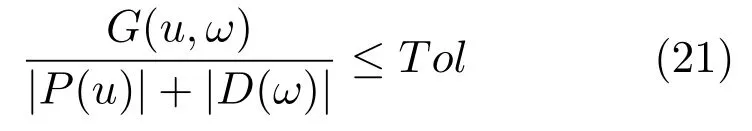
由算法1得到的u逼近最优解¯u，其中Tol是很小的正整数.从式（3），可以推出

本节给出算法在停止准则（21）下的数值表现，并与文献［22］中一些梯度投影算法比较.测试图像为Cameraman（256×256），Barbara（512×512）.在试验中，保真参数λ=0.045，ρmax=105，ρmin= 10-5，M=5，θ=10-4，α0=1，σ=0.5，Mµ=2.

测试如下算法.

1）文献［7］算法：半隐式梯度下降算法，τ= 0.248，记为Chambolle.

2）文献［22］的一些梯度投影算法：GPCL，GPLS，GPBBM，GPBBM（3），SQPBBM，GPBB-safe，GPBBNM，GPABB.

3）GPSSABB：算法1中自适应步长选择算法，ωk+1（·）由式（14）计算，γ=0.

4）MGPSSABB：算法1中自适应步长选择算法，ωk+1（·）由式（14）计算，γ=0.5.

图3分别给出Tol=10-4时Cameraman和Tol=10-6时Barbara图像恢复的结果.可以看出，算法1能够有效地去除噪音得到清晰的图像.表2和3给出Tol=10｛-2，-3，-4，-6｝的数值结果.其中GPBBNM表示在标准非单调线搜索下仅使用的梯度投影算法.GPABB是另一种形式的交替使用BB步长梯度投影算法.GPBBNM和GPABB算法是文献［22］中表现最好的算法，具体形式可以参考文献［22］.从这两个表中可以发现，Tol≤10-4时，新算法优势并不明显，甚至稍微慢于其他算法，如GPABB和GPBBNM.但Tol=10-6时，MGPSSABB的优势明显地表现出来，迭代步数和时间比GPABB和GPBBNM大大减少.图4给出了对偶间隙随时间变化的曲线.在算法满足停止准则终止时，从图4可以看出新算法CPU时间远少于GPABB和GPBBNM算法的CPU时间.这也证实了算法1在采用自适应BB步长和改进的线搜索下，能够更快地收敛于最优解，特别是精确恢复大尺寸图像和高精度要求时.

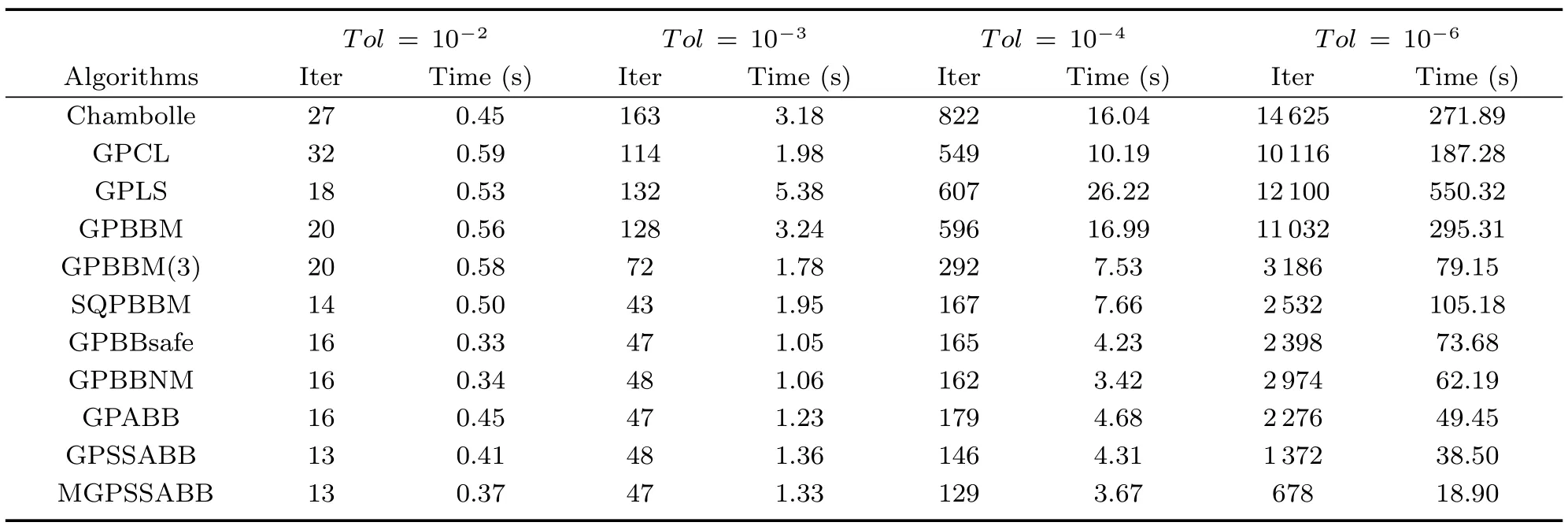
表2　Cameraman（256×256）迭代步数和CPU时间（秒）Table 2Number of iterations（Iter）and CPU time（s）of Cameraman（256×256）

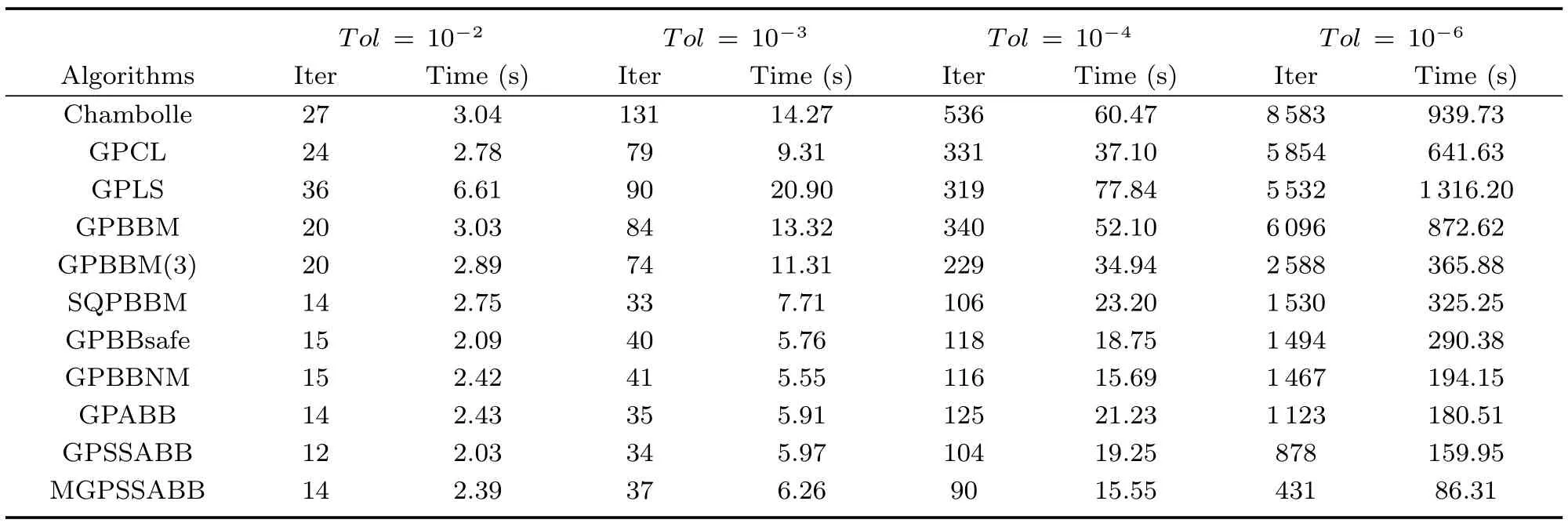
表3　Barbara（512×512）迭代步数和CPU时间（秒）Table 3Number of iterations（Iter）and CPU time（s）of Barbara（512×512）

图3　Cameraman（Tol=10-4）和Barbara（Tol=10-6）MGPSSABB的去噪结果Fig.3Denoising results of MGPSSABB of Cameraman（Tol=10-4）and Barbara（Tol=10-6）

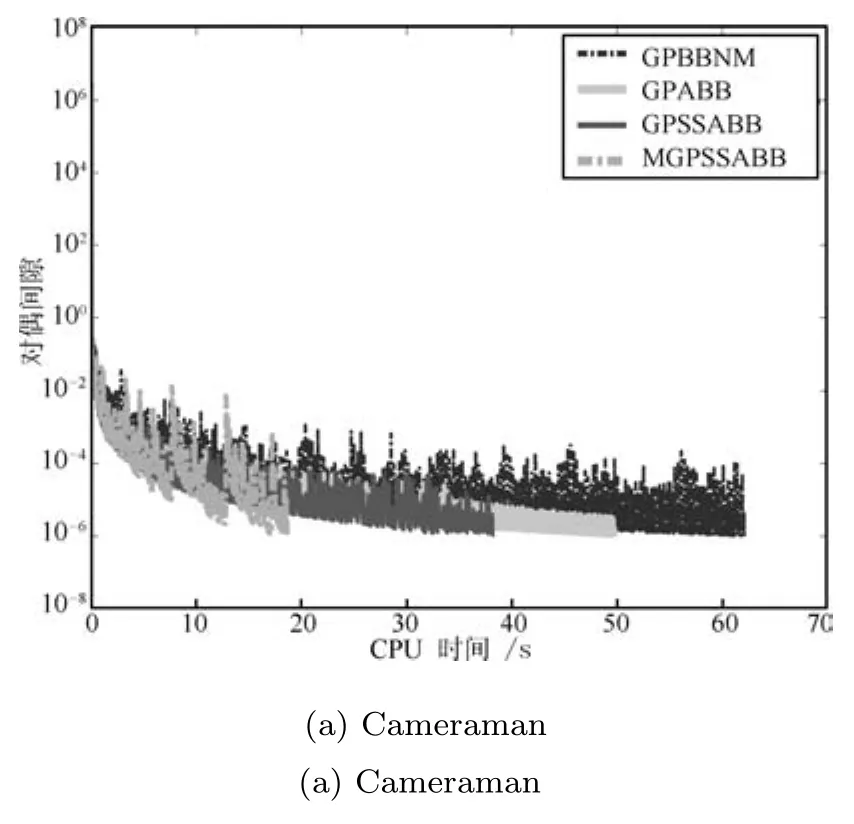
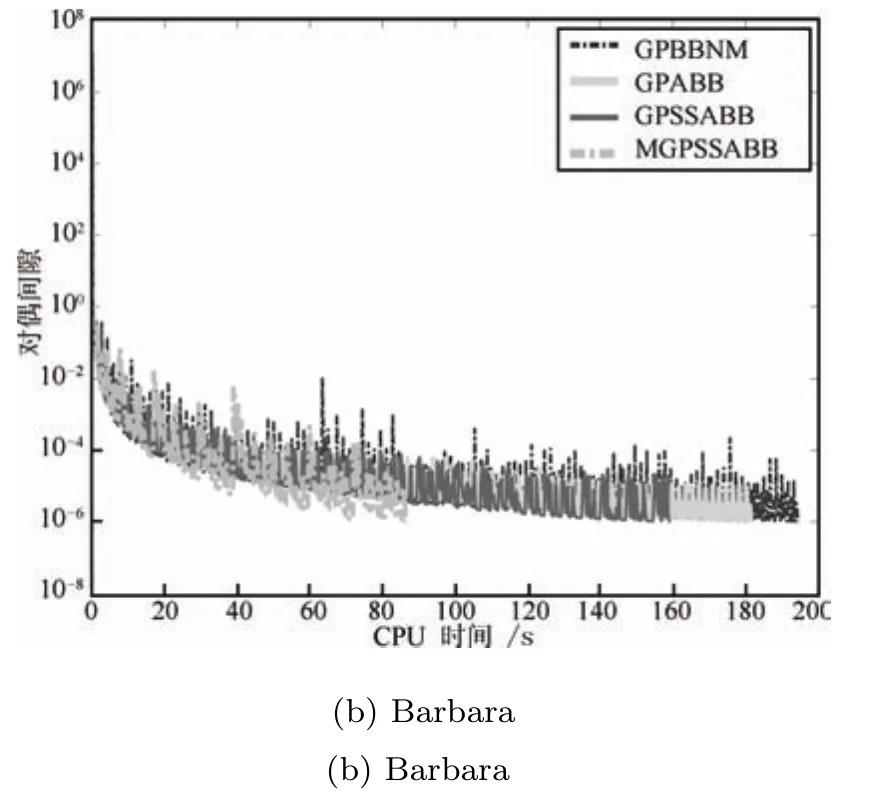
图4　四个算法的对偶间隙vs.CPU时间（秒）（Tol=10-6）Fig.4Duality gap vs.CPU time（s）for four algorithms（Tol=10-6）

通过图2和图4发现，相对范数和对偶间隙在迭代过程中不是单调下降.而这个非单调性是文献［16］指出的一个重要特征，它可能使算法更快地收敛于最优解.

最后，这两节的数值试验表明新提出的自适应步长梯度投影算法是有效的，优于其他几种梯度投影算法.

3　结论

针对全变差图像去噪问题，本文提出了一个自适应BB步长梯度投影算法，用著名的BB步长代替Chambolle梯度投影算法中的时间常数步长，并在改进的非单调线搜索下证明算法的全局收敛性.数值结果表明，新提的算法有效地改善了原始方法.从表1中数值结果可以看出，特别是对于大尺寸图像，新算法运行的CPU时间大约是Chambolle半隐式梯度投影方法的CPU时间的一半.并与其他梯度投影方法做比较，其数值表现也有明显优势.

References

1 Rudin L I，Osher S，Fatemi E.Nonlinear total variation based noise removal algorithms.Physica D：Nonlinear Phenomena，1992，60（1-4）：259-268

2 Aubert G，Kornprobst P.Mathematical Problems in Image Processing.Berlin：Springer，2002.

3 Chan T，Shen J H.Image Processing and Analysis：Variational，PDE，Wavelet，and Stochastic Methods.Philadelphia：SIAM，2005.

4 Wang Shi-Yan，Yu Hui-Min.Motion segmentation model based on total variation and split Bregman algorithm.Acta Automatica Sinica，2015，41（2）：396-404（王诗言，于慧敏.基于全变分的运动分割模型及分裂Bregman算法.自动化学报，2015，41（2）：396-404）

5 Zhang Rui，Feng Xiang-Chu，Wang Si-Qi，Chang Li-Hong. A sparse gradients field based image denoising algorithm via non-local means.Acta Automatica Sinica，2015，41（9）：1542-1552（张瑞，冯象初，王斯琪，常莉红.基于稀疏梯度场的非局部图像去噪算法.自动化学报，2015，41（9）：1542-1552）

6 Chan T F，Golub G H，Mulet P.A nonlinear primal-dual method for total variation-based image restoration.SIAM Journal on Scientific Computing，1999，20（6）：1964-1977

7 Chambolle A.An algorithm for total variation minimization and applications.Journal of Mathematical Imaging and Vision，2004，20（1）：89-97

8 Chambolle A.Total variation minimization and a class of binary MRF models.In：Proceedings of the 5th International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition.St.Augustine，FL，USA：Springer，2005.136-152

9 Ren Fu-Quan，Qiu Tian-Shuang.Blurred image restoration method based on second-order total generalized variation regularization.Acta Automatica Sinica，2015，41（6）：1166-1172（任福全，邱天爽.基于二阶广义全变差正则项的模糊图像恢复算法.自动化学报，2015，41（6）：1166-1172）

10 Zhang B X，Zhu Z B，Li S A.A modified spectral conjugate gradient projection algorithm for total variation image restoration.Applied Mathematics Letters，2014，27：26-35

11 Xiao Y H，Wu S Y，Qi L Q.Nonmonotone Barzilai-Borwein gradient algorithm for l1regularized nonsmooth minimization in compressive sensing.Journal of Scientific Computing，2014，61（1）：17-41

12 Loris I，Bertero M，De Mol C，Zanella R，Zanni L.Accelerating gradient projection methods for l1-constrained signal recovery by steplength selection rules.Applied and Computational Harmonic Analysis，2009，27（2）：247-254

13 Huang Y K，Liu H W，Zhou S.An efficient monotone projected Barzilai-Borwein method for nonnegative matrix factorization.Applied Mathematics Letters，2015，45：12-17

14 Xiao Y H，Jin Z F.An alternating direction method for linear-constrained matrix nuclear norm minimization.Numerical Linear Algebra with Applications，2012，19（3）：541-554

15 Yu G H，Qi L Q，Dai Y H.On nonmonotone Chambolle gradient projection algorithms for total variation image restoration.Journal of Mathematical Imaging and Vision，2009，35（2）：143-154

16 Dai Y H，Fletcher R.Projected Barzilai-Borwein methods for large-scale box-constrained quadratic programming.Numerische Mathematik，2005，100（1）：21-47

17 Bertsekas D P.Nonlinear Programming.Nashua：Athena Scientific，1999.

18 Frassoldati G，Zanghirati G，Zanni L.New adaptive stepsize selections in gradient methods.Journal of Industrial and Management Optimization，2008，4（2）：299-312

19 Barzilai J，Borwein J M.Two-point step size gradient methods.IMA Journal of Numerical Analysis，1988，8（1）：141-148

20 Birgin E G，Mart´ınez J M，Raydan M.Nonmonotone spectral projected gradient methods on convex sets.SIAM Journal on Optimization，2000，10（4）：1196-1211

21 Grippo L，Lampariello F，Licidi S.A nonmonotone line search technique for Newton＇s method.SIAM Journal on Numerical Analysis，1986，23（4）：707-716

22 Zhu M Q，Wright S J，Chan T F.Duality-based algorithms for total-variation image restoration.Computational Optimization and Applications，2010，47（3）：377-400

23 Ekeland I，T´emam R.Convex Analysis and Variational Problems.Philadelphia：SIAM，1999.

张本鑫桂林电子科技大学电子工程与自动化学院博士研究生.主要研究方向为最优化方法和变分法在图像处理中的应用.

E-mail：zbx913@163.com

（ZHANGBen-XinPh.D.candidate at the School of Electronic Engineering and Automation，Guilin University of Electronic Technology.His research interest covers optimization algorithm，variational method and their applications in image processing.）

朱志斌桂林电子科技大学数学与计算科学学院教授.2004年获西安交通大学理学博士学位.主要研究方向为最优化方法及其在图像处理和反问题中的应用.本文通信作者.

E-mail：optimization_zhu@163.com

（ZHUZhi-BinProfessor at the School of Mathematics and Computing Science，Guilin University of Electronic Technology.He received his Ph.D.degree in applied mathematics from Xi＇an Jiaotong University in 2004.His research interest covers optimization and their applications in image processing and its inverse problem.Corresponding author of this paper.）

Gradient Projection Algorithm for Total Variation Image Restoration by Adaptive Steplength Selection Rules

ZHANG Ben-Xin1，2ZHU Zhi-Bin3，4

We propose a new gradient projection algorithm for image denoising based on the dual of total variation. The new method exploits nonmonotone line-search and adaptive steplength selection based on strategies for alternation of the well-known Barzilai-Borwein rules.The proposed method is much faster than the Chambolle＇s gradient projection algorithm.Numerical results illustrate the efficiency of this method.

Gradient projection，total variation，adaptive steplength selection，new line search，image restoration

Manuscript March 24，2015；accepted April 28，2016

10.16383/j.aas.2016.c150146

Zhang Ben-Xin，Zhu Zhi-Bin.Gradient projection algorithm for total variation image restoration by adaptive steplength selection rules.Acta Automatica Sinica，2016，42（9）：1347-1355

2015-03-24录用日期2016-04-28

国家自然科学基金（11361018，11461015），广西省自然科学基金（2014GXNSFFA118001），广西自动检测技术与仪器重点实验室基金（YQ15112，YQ16112），广西高校科研一般项目（KY2016YB167），桂林市科技攻关项目（20140127-2），广西和桂林电子科技大学研究生教育创新计划项目（YJCXB201502）资助

SupportedbyNationalNaturalScienceFoundationof China（11361018，11461015），NaturalScienceFoundation of Guangxi Province（2014GXNSFFA118001），Guangxi Key Laboratory of Automatic Detecting Technology and Instruments（YQ15112，YQ16112），Guangxi Education Scientific Research Program（KY2016YB167），Guilin Science and Technology Project（20140127-2），Innovation Project of Guangxi and Guilin University of Electronic Technology Graduate Education（YJCXB201502）

本文责任编委黄庆明

Recommended by Associate Editor HUANG Qing-Ming

1.桂林电子科技大学电子工程与自动化学院桂林5410042.桂林电子科技大学广西自动检测技术与仪器重点实验室桂林5410043.桂林电子科技大学数学与计算科学学院桂林5410044.桂林电子科技大学广西高校数据分析与计算重点实验室桂林541004

1.School of Electronic Engineering and Automation，Guilin University of Electronic Technology，Guilin 5410042.Guangxi Key Laboratory of Automatic Detecting Technology and Instruments，Guilin University of Electronic Technology，Guilin 541004 3.School of Mathematics and Computing Science，Guilin University of Electronic Technology，Guilin 5410044.Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation，Guilin University of Electronic Technology，Guilin 541004