基于数据驱动的微小故障诊断方法综述

文成林　吕菲亚　包哲静　刘妹琴

基于数据驱动的微小故障诊断方法综述

文成林1吕菲亚2包哲静2刘妹琴2

能否及时诊断出微小故障是保障系统安全运行并抑制故障恶化的关键，本文针对微小故障幅值低、易被系统扰动和噪声掩盖等特点，从数据驱动的角度对现有研究进行综述.并将其分为三大类：基于统计分析的微小故障诊断技术、基于信号处理的微小故障诊断技术和基于人工智能的微小故障诊断技术，进而对不同方法的基本研究思想、研究进展、应用以及局限性予以介绍.最后不仅指出复杂系统微小故障诊断研究中的现存问题，而且从增加新的信息、挖掘未利用的隐含信息和采用新的数学工具三个角度进行展望，提出基于关联性分析、基于多源信息融合、基于机器学习和基于时频分析四个值得探究的微小故障诊断思想.

微小故障诊断，数据驱动，统计分析，信号处理，人工智能

引用格式文成林，吕菲亚，包哲静，刘妹琴.基于数据驱动的微小故障诊断方法综述.自动化学报，2016，42（9）：1285-1299

随着现代控制系统的设备复杂化和规模大型化，有关系统的异常检测和故障诊断一直是学术界关注的重点问题.系统一旦发生故障，若不能及时发现并处理，将造成巨大的经济损失和人员伤亡.例如美国石油化工企业每年因机械故障直接损失200亿美元；2015年2月4日，台湾复兴航空客机因两个发动机同时失效导致断油坠落，造成35人以上死亡等.如果能及时在工业运行过程的可控范围内检测出微小或早期故障并隔离报警，将有效避免异常事件的发生，减少生产力损失，因而对复杂系统进行合理的故障诊断是一个亟待解决的关键问题.

故障的初始定义是指在一个过程中，观测变量或计算参数对可接受范围的偏离［1］.考虑到故障的演变过程，可分为显著性故障和微小故障.微小故障通常具有幅值低、故障特性不明显、易被未知扰动和噪声掩盖等特点［2］.一方面包括始终偏离正常运行状态程度较小，经过时间的积累，却可危及系统安全运行的潜在故障，如电力驱动系统中由轴承转轮内环缺陷引起的故障［3-4］；另一方面包括对系统性能影响较小的早期故障，早期故障在故障演变过程中有幅值限制，一旦超过最大值就发展为显著故障，如设备中因部件磨损导致的故障［5］、变压器中的电弧放电故障［6］.微小故障具有隐蔽性和随机性，初期特征极其不明显，然而任何一个局部的微小故障都可能通过设备及子系统之间的连通路径进行传播和扩散，经演变导致设备的误报警或误切换.特别是后一类型的微小故障，有可能在短时间内突变至较大幅值进而导致系统性能退化.

事实上，微小故障与显著故障是相对而言的，在故障存在的前提下，现有的诊断方法诊断不出来的故障即可被视为微小故障.相对于传统的故障诊断方法，微小故障诊断是一类更精细的诊断形式，需要着重增大故障与噪声之间的信噪比，去除扰动和噪声对微小故障的掩盖，因而诊断难度也更大.针对复杂系统的微小故障诊断，现有的文献方法集中包括常规的分析方法［7-8］、统计方法［9-10］和智能方法［11-12］.文献［13-14］将微小故障分为缓变微小故障、突变微小故障和间歇性微小故障，并将微小故障诊断方法分为定性诊断方法、定量诊断方法和半定性半定量的诊断方法.目前较为常见的分类是：基于解析模型的故障诊断技术、基于知识的故障诊断技术和基于数据驱动的故障诊断技术.

基于模型的微小故障诊断技术是从系统的本质特性出发，以期对故障达到实时性的诊断.微小故障通常与模型参数直接相关，随着对系统故障演化机理的逐步理解，进而实现对模型的修正以提高诊断精度.然而，在实际的工程化应用中，例如化工产业、电力系统、大型船舶等复杂多变量系统，通常要求所构建的数学模型具有高精度性，而基于解析模型的微小故障诊断方法多数是利用系统残差对其局部子系统构建数学模型进行状态估计、在线近似等，难以确保高精度.同时，由于建模过程中难以避免误差和未知干扰，很难同时保证干扰鲁棒性和故障灵敏度，特别是对于复杂的动态系统，如果变量彼此耦合，建立模型的代价就更高.因此基于模型的微小故障诊断技术在实际应用中具有局限性.

基于知识的微小故障诊断技术依赖于相关领域专家的经验知识，分为定性方法和定量方法.定性方法多是基于状态、属性等非量化特征进行诊断，诊断的准确程度受知识库中专家经验的丰富程度影响，并依赖于专家知识水平的高低.但鉴于系统的动态复杂性、专家经验和知识的局限性以及对知识规则化表述的困难性，使得诊断知识库并不完备，也就是说，当遇到一个全新的故障现象时，知识库内没有相关规则与之对应，同时，系统缺乏自学习和自完善能力，现行的用于故障诊断的专家系统在运行中不能从诊断的实例中学习获得新的知识，且对系统设计的一些边缘性问题的求解显得较为脆弱和敏感.微小故障属于弱信号，很难由定性的方法直接推理，因而对于微小故障具有一定的局限性.鉴于定量方法所需的知识源于对大量数据潜在信息的分析与挖掘，本文将其归为基于数据的故障诊断方法.

随着信息技术和计算方法的发展，以及集散控制系统在工业中的大量应用，系统监控变量和状态数据大幅度增加，使得对过程的监控管理已无法依靠传统的机理分析方法建立精确的数学模型；同时集散控制系统具有多闭环、高耦合、强干扰以及多源不确定性等特点，尚无法得到全面可靠的故障因果逻辑关系，因此，对系统运行中的监控数据进行分析，以此推演故障的演变机理更为直接有效.特别是在大数据时代背景下，基于模型、知识的微小故障诊断技术由于侧重对因果关系的寻求，适用于具有较少的输入、输出、状态变量的系统；而针对大数据具有的海量性、多样性和快速性等特点，基于数据驱动的故障诊断方法更为适用，表现在其对多元信息处理的直接性和有效性，侧重对数据间相关关系的关注.

基于数据驱动的微小故障诊断技术并不依赖系统的先验知识，例如数学模型和专家经验，该技术以采集到的不同来源和不同类型的监测数据作为基底，利用各种数据挖掘技术获取其中隐含的有用信息，表征系统运行的正常模式和故障模式，进而达到检测与诊断的目的，成为目前较为实用的诊断技术.系统发生故障必然会反映在监测数据上，监测数据包括当前时刻的采样数据（即在线数据）以及大量的历史数据.在线数据反映了系统当前的时变特性，历史数据包含了监测对象的各种过程模式.理论上，只要对监测数据进行合理且足够深度的挖掘，便可获得更为细节化的故障特征，适用于微小故障的诊断.基于数据的微小故障诊断方法能够相对准确识别故障并辨识故障发生的严重性，常用方法包括机器学习法、多元统计分析法、信号处理法以及信息融合法等［13］.

本文侧重从定量的角度出发讨论基于数据驱动的微小故障诊断技术，并将其细分为基于统计分析的微小故障诊断方法、基于信号处理的微小故障诊断方法和基于人工智能的微小故障诊断方法，如图1所示.下文将分别探究这三类方法的理论知识与研究现状，分析不同算法的局限性和挑战性，并概述复杂系统微小故障诊断中现存的问题，着重分析基于数据驱动的微小故障研究趋势，展望其发展方向.本文讨论的微小故障实时诊断与预测技术均假定故障可被感知并能被分离.可被感知是指微小故障在一定程度上影响系统的状态和输出；能被分离是指依据现有信息可以指示故障发生部位和发生机理.

1　基于数据驱动的微小故障诊断技术研究现状

基于数据驱动的微小故障诊断技术是在一定的代价函数约束下，通过对历史数据进行学习和挖掘，得到相应的数学模型关系，进而逼近系统数据中所隐含的映射机制，以此进行微小故障的检测和诊断［15］.

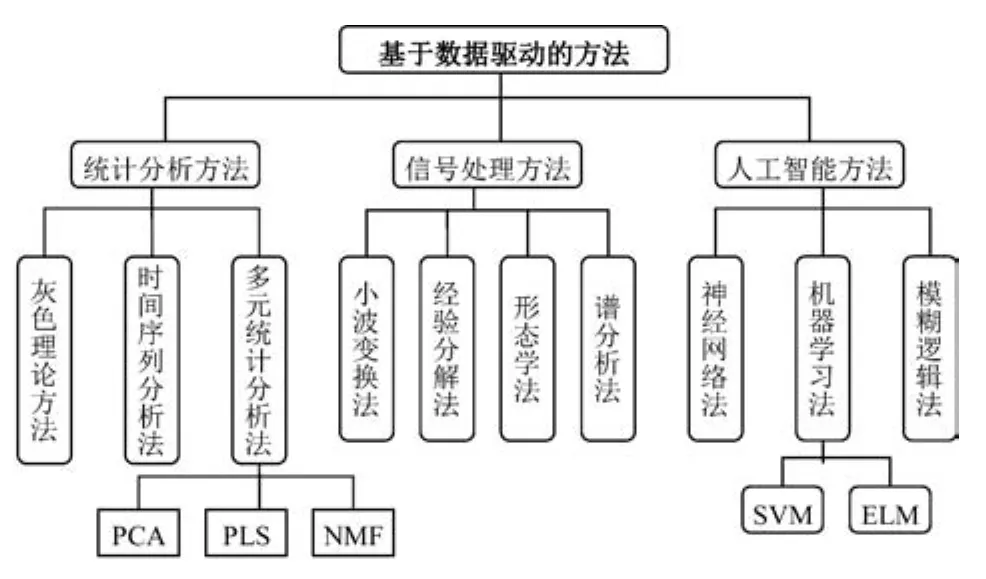
图1　基于数据驱动的微小故障诊断方法分类Fig.1The classification of data-driven based incipient fault diagnosis

1.1基于统计分析的微小故障诊断

基于统计分析的方法主要是对历史过程数据进行统计分析，为每个样本计算对应的监控统计量，并根据正常样本估算出的监控指标置信限来分析当前样本的运行状态［16］，包括基于单变量的统计监控和基于多变量的统计监控技术.基于单变量的统计监控方法虽然容易实现，但忽略了变量之间的相关性信息，只能用于数据维数较小时的监控.而基于多变量的统计分析能较好刻画并利用变量之间的相关性，适用于高维系统的故障检测与诊断.基于多变量统计分析的代表性方法包括主元分析、偏最小二乘方法、独立元分析和非负矩阵分解等.

1.1.1主元分析方法

主元分析（Principal components analysis，PCA）方法是应用最广泛的多元统计分析方法，最初由Pearson提出［17］，主要用于分析处理具有高度线性相关性的测量数据［18］.PCA方法通过映射达到降维的目的，并使得变换后的主元子空间反映的是监测变量的主要变化，残差子空间反映的是监测过程中的噪声和干扰等［18-19］.

Wise等［20］最早将PCA方法用于异常监控，其基本原理是采集处于正常工况下的过程数据Xnormal，对其进行归一化处理为X，然后进行PCA建立统计分析模型

在微小故障诊断方面，文献［21］从整个工业流程角度出发，使用PCA技术刻画蒸汽发电机的标定操作曲面，考虑了变量在物理含义上的相关性；文献［22］针对具有缓变性、不确定性的焚烧炉早期故障，基于PCA提出了专门用于检测固体废物的框架；文献［23］针对化工过程中变量的相关性，将PCA技术与单变量指数加权滑动平均相结合；传统主元分析方法忽视了量纲对系统的影响，文献［24］针对这一问题提出相对主元分析，根据系统的先验信息分析和确定各分量的重要程度，赋以系统各分量相应的权值，实现对系统中微小故障的检测；针对PCA的模式复合效应在多级微小故障诊断上的局限性，文献［25］提出了PCA投影框架下的多级微小故障诊断；鉴于微小故障与正常状态之间的偏离较小，文献［26］结合概率分布度量，采用Kullback-Leibler测度量化潜在分数与参照分数之间的残差，提出了适用于微小故障的PCA算法控制限；文献［27］在文献［26］的基础上提出一个分析模型，根据散度估计微小故障与噪声接近的量级，辨识微小故障的发生.

PCA方法需要假设数据服从高斯分布，而工业系统的数据未必完全服从高斯分布，例如当监测变量是间接测量时.同时，传统PCA方法属于混合潜变量分析方法，不能直接处理非线性和多模态问题，即便是检测出故障，也难以确定故障的发生源.特别地，PCA采用T2和SPE等统计量作为评价指标会扩大检测区域，不能很好地描述正常数据分布，例如在三维空间中，判定阈值的设置使得检测区域由原本的椭球形判定区域变为其外切的长方体，此时微小故障由于偏离正常状态较小更难以被检测出，因而基于PCA方法进行微小故障诊断在实际应用中更加困难.

1.1.2独立元分析法

独立元分析（Independent component analysis，ICA）方法是针对具有非正态分布的多变量系统提出的.鉴于PCA方法提取的主元虽然不相关，却也并不相互独立，ICA把多光谱或者高光谱数据转换成不相关且相互独立的部分，在降维的同时发现并分离出数据中隐藏的噪声信息［28］.当感兴趣信号的能量和强度相对于数据中其他信号较弱时，这种变换比PCA得到的结果更加有效.另外，ICA不仅可以提取互相独立的主元变量，而且可以提取高阶统计量信息［28］.

Kano等［29］最早将ICA方法用于异常监控，由等概率密度曲线确定联合分布的控制置信限.为了充分利用过程中普遍存在的高斯和非高斯信息，文献［30］将PCA与ICA相结合，对统计量进行重构，并提出了混合相似度因子，实现微小故障的诊断；针对多个故障信号相互耦合的情况，文献［31］利用频域的ICA技术实现变速箱中的多维振动信号的分离，然后结合Morlet小波进行滤波处理得到微小故障的特征；文献［32］基于重建的相位空间中的相位点训练ICA的基，并根据训练好的基对转化系数的相关性进行量化，基于相位谱表征新的故障特征，充分利用动态多变量系统的高阶统计信息；文献［33］针对不确定的信号和误差分布，提出了基于局部ICA的方法，利用回归技术估计故障对异常状态的贡献；文献［34］将ICA与Kurtogram算法结合以获得不同源的包络成分，弥补包络分析在处理滚动轴承和齿轮具有多故障情况下的不足.

ICA方法虽然不要求数据服从高斯分布，但要求数据在时间序列上独立，而工业数据的采集大都是依据时间采样，这就使得ICA在处理数据的过程中相对损失了时间上的信息，因而基于ICA方法的微小故障诊断会忽视故障数据在时间上的相关性.

1.1.3偏最小二乘方法

偏最小二乘（Partial least square，PLS）方法是基于PCA的多变量回归算法，其思想是同时对输入矩阵X∈Rm×n和输出矩阵Y∈Rm×p进行正交分解，目的是使得分解后的主元的协方差最大，也就是使输出信息可以最大限度由输入表征［35］. Kresta等最早将PLS方法用于异常监控［36］，又称潜空间投影.在PLS方法的改进性分析中，较为常用的是非线性迭代部分最小二乘，通过逐步迭代交换实现对输入和输出矩阵的分解，这种互交换模式加强主元间的对应关系［37］.由于PLS是由输出变量引导输入样本空间的分解，因而比PCA具有更强的输入解释能力.同时，PLS模型解唯一.为了扩展PLS在故障诊断领域的应用，文献［38］提出动态PLS方法，解决了实际生产过程中存在的时变性问题；针对可预测的输出子空间和不可预测的剩余输出子空间，文献［39］构造了能够使输入和输出空间同时投影的并发式潜在投影结构；文献［40］将局部统计方法与PLS框架相结合，用于监控复杂化学系统中底层模型的变化，而不是对记录的输入/输出数据进行直接分析，优势是参数变化可以非高斯，而且确保非平稳过程不会产生误报.

以上三种方法（PCA、ICA、PLS），都是通过基变换将数据映射到另一个空间达到降维的目的，在降维过程中通过设置阈值保存信息量，难免会丢失原有数据的微小特征；而且基于这三种方法的故障诊断又都是根据统计量设置阈值判断故障是否发生，同样会忽视数据微小特征对结果的影响；进一步，这三种方法在实际应用中的降维也大都采用维数的线性约减，并不适用于复杂的非线性系统.对此，虽然大量研究提出了各式各样的解决方案［41-42］，但也各有其局限性，特别是当微小故障淹没于非高斯、多模态、非线性数据中时，仍难以得到较好的诊断效果.

1.1.4非负矩阵分解方法

考虑到PCA、PLS等不能很好地描述数据的隐形结构，Lee等［43］提出了非负矩阵分解（Nonnegative matrix factor，NMF）法，NMF在一定程度上实现了非线性的维数约减，并能很好地反映样本的局部特征，同时非负性的约束有利于分解结构稀疏性的呈现［44］.有关NMF方法在故障诊断领域的应用，主要体现在维数的非线性约减，文献［45］将NMF方法应用于行星多变量光谱的振动检测；对于高速旋转机械，振动分析是应用最广泛的状态监控技术，针对振动信号的不稳定性和随机性，文献［46］将NMF方法与神经网络相结合，用于柴油缸的状态诊断；传统的NMF在处理二维矩阵时需要将其转换成一维向量，可能造成结构信息的丢失.对此，文献［47］提出了二维NMF方法，并与推广的S变化相结合，用于滚动轴承微小故障的诊断.

NMF方法对于微小故障的诊断具有一定的有效性，但它侧重对较为重要的局部特征的提取，并不能充分反映出样本的全局特征，易于忽视或者掩盖故障发生后对某些变量的微小影响，这些微小影响需要通过对监控量全局分析进行挖掘，因而目前在微小故障诊断领域的应用相对较少.

1.1.5时间序列分析方法

时间序列分析（Time series analysis，TSA）方法是动态数据分析处理的一种重要的方法，通过分析时间序列中的潜在信息来估算其过程的统计规律性，主要包括频域分析和时域分析两大类方法［48-49］.基于时间序列分析的微小故障诊断技术以工业过程中的长期监测的历史数据作为时间序列，建立数据随时间变化的动态模型，基于此模型进行故障诊断.

隐马尔科夫模型是一种具有较强模式分类能力的时间序列统计模型，文献［50］基于其对涡轮发动机发生在启动和加速暂态下的早期故障进行检测和诊断；由于脉冲在故障频率中呈现周期性，文献［51］在小波变换提取滚动轴承故障特征的前提下，使用隐马尔科夫模型对振动信号进行模式识别；文献［52］基于隐马尔科夫模型在观测序列和可能的状态序列之间增加映射，降低模型参数估计的代价，简化了故障诊断模型的结构；由于慢时标异常行为的早期检测可通过观测系统运行的快时标时间序列数据获得，文献［53］采用基于符号的时间序列分析异常检测方法检测发生在螺旋伞齿轮箱中齿轮或轴承上的早期微小故障；文献［54］将任意分布的初始数据基于模糊聚类方法变换为可用beta分布近似的时间序列，然后使用时间序列的变化点检测技术实现对异步感应电机定子绕组早期微小故障的检测；鉴于异步电机由内部短路和由绝缘分布引起的故障相互耦合，文献［55］使用离散逆小波变换提取相关频段，并在不同故障状态下对当前序列进行重建或滤波，然后进行趋势波动分析，最终实现微小故障的有效区分.

基于时间序列分析的故障诊断方法简单易行，便于掌握，但相对而言准确性差，一般只适用于短期的分析预测.而微小故障由于偏离正常运行状态的幅度较小，对其相关性分析需要较长时间的跟踪，以避免虚假故障造成的误判.

1.1.6灰色理论方法

传统的系统理论局限于对系统确定性问题的研究，针对具有不确定性的复杂系统，灰色理论方法应运而生.灰色理论依据认识、信息和决策的层次判定系统是否会出现信息不完全的情况［56］.基于灰色理论方法的微小故障诊断技术是通过微分拟合构建合理的数学模型，并依据某些特定的算法将杂乱无章的原始数据规律化，进而预测监控系统中是否存在微小故障.实际上，该方法主要用于上文叙述的第二类微小故障，是对系统发生较大故障的潜在可能性的一种预测［57］.

溶解气体分析技术是油浸式电力变压器微小故障检测最常用的技术，但由于高花费，年使用次数少，造成可用的输入信息不多，文献［57］将物元模型与可拓理论相结合，依据可拓关联函数隶属度的高低进行状态预测，再依赖预测值实现电力变压器中的热故障、局部放电等早期微小故障的检测；文献［58］采用灰色预测模型GM（1，2）预测可燃和非可燃气体的变化趋势，通过灰色聚类分析实现油浸式电力变压器内部早期故障的有效诊断，提高了早期微小故障的预测精度，并具有较好的稳定性；鉴于质子交换膜燃料电池反应时间的延迟，文献［59］基于灰色预测模型进行状态监控，并根据对特征的预测值实现对操作条件的预测，进而实现可拓性诊断.

基于灰色理论的微小故障诊断方法不需要依赖大量的样本数据建模，原理简单且运算方便.但是仅依靠小样本信息进行趋势分析，其泛化能力不足，当预测对象较多，或者呈现非线性增长时，预测结果就有可能会出现较大的偏差，特别地，微小故障的运动趋势极其不明显，很难被提炼，因而需要与其他方法相结合使用.

1.2基于信号处理的微小故障诊断

当工业过程发生故障时，信号的幅值、相位和频率等会发生不可预期的变化.故障诊断技术通过利用大量丰富的专家经验知识和系统运行过程中的各种状态信息进行分析和处理，得到系统运行状况和故障状况的综合性评价，从这个角度看，故障诊断实质也是典型的信号分析处理过程.目前，基于信号处理的微小故障诊断技术主要有小波变换法、经验模式分解法、形态信号处理法和谱分析法等［60］.

1.2.1小波变换法

小波变换（Wavelet transform，WT）法不仅继承和发展了短时傅里叶变换局部化的思想，而且克服了傅里叶变换中窗口大小不随频率变化等缺点［61］.基于小波变换法进行微小故障诊断的思想是：鉴于小波变换的分辨率可变特性，通过伸缩和平移等运算对故障信号逐步进行多尺度以及多分辨率地细化分析，达到对高频处时间和低频处频率的细分，从而聚焦到故障信号的微小细节特征信息，用于微小故障诊断［62］.

鉴于小波变换法的主要优势在于能够根据时间分辨率和频率分辨率分辨出信号的瞬时特征，并保留信号的主要频域成分，以滤除噪声影响，小波变换法更适合于非稳定和非周期宽带信号处理.振动信号是典型的非线性随机信号，为了表示其所有可能的瞬变类型，文献［63］利用离散小波变换提取信号特征作为神经网络的输入，实现对变速器的微小故障诊断；文献［64］提出将离散小波变换和包络分析相结合提取振动信号的特征谱，然后依据光谱互相关系数辨识不同的操作状态，进而实现对滚动轴承微小故障的诊断；针对变速器发生局部微小故障时具有的多重调幅—调频机制特性，文献［65］提出了自适应的小波脊解调算法，解调得到瞬时的振幅和频率；文献［8］综述了小波变换技术在回转式机械微小故障诊断中的发展与应用；文献［66］综述了连续小波变换在滚动轴承微小故障诊断中的发展与应用，并构建决策树以选取最优的小波提高分类精度.

受傅里叶分析理论对非线性非平稳信号的局限性，小波变换后也容易出现假频和虚假信号，而且受Heisenberg不确定原理的限制，小波变换不能精确描述频率随时间的变化.进一步讲，傅里叶变换和小波变换都是以积分的形式进行，其几何意义是对瞬时信息的一种平均，而微小故障由于幅值较小的特点很容易被平滑或者弱化掉其中的部分信息.再者，小波基函数的有限长度会引起微小故障信号的能量泄露.此外，这两种变换都只能反映出状态信号映射到频域后的特性，并不能展示故障信号从时域到频域的逐步变化过程，没有挖掘信号在转换过程中的瞬时频率等特征.因而，基于这两种变换的故障诊断技术会忽视故障信号随时间变化的频率分布特征，不利于对微小故障特征信息的深度挖掘.

1.2.2谱分析法

谱分析（Spectrum analysis，SA）法是将模态分析的结果和已知谱相联系，用于计算结构响应的分析方法［67］.在工业故障监控中，不同类型的过程故障会引发监控信号不同的频谱特征，基于谱分析法的微小故障诊断就是利用对信号的功率谱、倒频谱、高阶谱等的分析来进行监控诊断，其中以频域的谱分析最为常用［68］.

故障对振动信号的影响会使其产生给定频率的调幅，例如包络检测信号的频谱在故障频率处会呈现较大的峰值，而在其他频率上相对较平缓.文献［69］是将谱分析法用于诊断旋转机械早期故障的最早文献；文献［70］综述了在电机故障诊断中，除了局部线路电流的特定谐波分量，速度、力矩、噪声、振动等信号的频谱信息也可以被利用；文献［71］结合小波包技术的多维谱分析方法以辨识故障源，实现对非平稳振动的微小故障信号的早期检测，克服了基于傅里叶方法的时变特性在非平稳系统中的局限性；针对轴承振动信号的微小故障诊断，文献［72］分别使用基于奇异值和能量特征两种谱分解方法进行特征提取，然后结合人工神经网络进行故障诊断，说明了基于奇异值谱分解的信号特征提取方法对噪声免疫；由于高阶谱对高斯噪声具有很好的抑制能力，并具有保持非线性系统相位信息的特点，文献［73］提出了基于统计能量分析的高频识别方法，并描述了在每个解析频段负载功率谱都是定值与线性振动的假设下，由输入功率推导的负载功率谱的方法，指出在定值假设下计算的负载功率谱与实际测量值基本一致；由于滚动轴承故障具有较低的信噪比，文献［3］提出了振动光谱成像技术，将似稳时间振动信号的光谱内容的标准振幅转换成光谱图像，以此加强特征的质量，并验证了不同信噪比下振动光谱成像特征的鲁棒性.

从某种程度上讲，奇异谱分析也属于时间序列分析［74］，因而在微小故障诊断中有着相似的局限性.

1.2.3经验模式分解法

经验模式分解（Empirical mode decomposition，EMD）法由Huang等［75］提出，依据数据自身的时间尺度特征进行信号分解，其技术关键是如何自适应地将复杂的高维信号分解成有限个本征模式函数［76］，并确保分解出的各个本征模式函数分量都能包含原信号不同时间尺度上的局部特征信息.

基于EMD法的微小故障诊断思路是：首先对非平稳的监测数据进行平稳化处理，然后进行Hilbert变换得到频谱图，分辩出具有物理意义的频率，再进行模式分析.文献［77］提出将Hilbert-Huang变换用于处理定子电流，首先通过经验模式分解估计本征模式函数，然后利用Hilbert变换计算瞬时振幅和频率，并将瞬时振幅的能量作为故障指示器，用于感应电机中轴承微小故障的检测；鉴于弱信号的低幅值和低信噪比，文献［78］将小波变换与EMD相结合，基于样本熵和奇异值分解，提出了针对听觉信号的微小故障诊断技术，降低了信噪比，并改进了奇异值分解；为了抑制EMD的端点效应，文献［79］根据弱信号检测理论，将小波分析嵌入到Hilbert-Huang变换的迭代过程，以降低筛选过程中的迭代误差和噪声信号，同时基于相关分析提出了新的终止准则，用于移除不良本征模式函数，进而用于微小故障检测和心电图信号分析；文献［80］综述了EMD在旋转电机故障诊断中的应用，并展望了其未来的研究方向.

理论上，经验模式分解法可用于任何类型信号的分解，在处理非线性和非平稳信号序列时具有明显的优势和很高的信噪比.但是，EMD法并没有严格的数学模型作为支撑，而且存在难以避免的端点效应，当时间尺度较长时，端点效应会随着分解的不断进行向内传播污染；此外，由EMD分解得到的本征模式函数分量可能包含不同时间尺度的故障信号，或者故障信号存在于不同的本征模式函数中，从而引起时频分布的混叠.在微小故障诊断研究中，微小故障信号由于幅值较小易于被这些端点效应以及模态混叠覆盖而引发误判.特别地，EMD法是根据离散信号的极值点确定的特征尺度进行分解，即便是小的噪声也会对分解产生较大影响.

1.2.4形态信号处理法

形态信号处理（Morphological signal processing，MSP）法属于非线性时域空间上的信号处理方法，建立在格论和拓扑学基础之上［81］，对信号的局部几何特征较为敏感，能够高效分析处理脉冲信号.基于MSP法的微小故障诊断方法的思想是：通过构造一个合适的探针，也就是结构元素，让其在信号中不断移动，以探寻具有物理意义的信号相互之间的关联性，进而提取这些特征用于微小故障的诊断［82］.

MSP法是基于集合进行运算，因而计算简单且适合于并行计算，具有一定的灵活性.由于旋转机械的故障会引起振动信号的脉冲呈现弱周期性，文献［83］采用小波变换进行滤波以消除噪声干扰、增强脉冲特征，进而使用MSP法根据形态闭合算子和局部最大算法再次处理滤波后所得信号，提取周期性脉冲.同时，MSP法由于需要有关信号的先验知识去定义扁平结构元素的长度，为了平滑噪声和提取振动信号的脉冲，文献［84］将闭运算和开运算的均值作为形态学算子，采用平面和零值作为结构元素的形状和高度，并对结构元素优化后的长度定义了新的标准；为了挖掘故障信号更多潜在的多尺度信息，文献［85］基于MSP设计了8种多尺度形态学滤波器，以特征频率强度系数作为评价指标，探究了在齿轮故障检测中的应用；针对滚动轴承的微小故障检测，文献［86］提出了权重多尺度形态梯度滤波技术，基于大尺度降低噪声、小尺度保留脉冲形状细节信息，以此实现在线状态监控与故障诊断.

MSP法本质上是一类非线性滤波器，从几何意义上讲，它是基于集合的局部平均运算，因而基于MSP法进行微小故障诊断时，难以避免微小故障信号被形态滤波器弱化的情况.同时，MSP法对信号形状的依赖性较强，当由故障产生的脉冲完全被噪声淹没时，该方法难以施展，因而针对微小故障的诊断可以结合其他方法先去噪后再应用.

1.3基于人工智能的微小故障诊断

由于故障类型和故障征兆之间不存在简单的对应关系，针对系统的不确定性和复杂性，基于人工智能的故障诊断技术较为适用.基于人工智能的故障诊断主要是通过工业过程的正常数据以及故障数据来训练各类学习算法，进而实现微小故障诊断的目的.其技术难点在于如何从监测的历史数据中提取出重要的特征信息，包括这些特征的实时变化、阶段性变化和趋势性变化等.

1.3.1人工神经网络法

人工神经网络（Artificial neuron network，ANN）的研究源于20世纪40年代心理学家M c-Culloch和数理逻辑学家Pitts提出的M-P模型［87］，具有自学习和自适应的特性，在工业系统的异常监控领域取得了较为广泛的研究与应用.基于神经网络的微小故障诊断方法的思想是：通过网络层间的学习建立故障征兆与故障类型的映射关系，使输入层的节点对应故障征兆，输出层的节点对应故障类型，从而实现由故障征兆到故障类型的推理过程［88］.

神经网络的强大之处还在于其鲁棒性和容错性，文献［89］最早提出将ANN用于直流电机的早期微小故障检测；针对油浸式电力变压器中的微小故障，文献［90］依据三种可燃气体的比率信息构建几个不同的ANN模型，并选取最优的结构进行故障分类；鉴于神经网络模型的解释能力较差，文献［91］使用案例法作为函数逼近ANN的信息提取规则，以绝缘油内部可燃气体浓度作为输入，实现变压器微小故障的实时检测；感应电机的状态监控需要一个简单可靠且能辨识多类故障的探测器，文献［92］使用小波分析和傅里叶变换对振动信号进行预处理，提取故障特征，然后利用基于径向基函数的神经网络，从故障的本质上实现故障的分类；针对生产系统中成分的退化和机械的磨损，文献［93］通过时频分析技术在频域上利用ANN实现微小故障的检测和诊断.

虽然神经网络可以根据需求设置网络结构，以任意精度逼近非线性函数［94］，但是网络的学习需要大量的故障样本，故对无法获得大量工业过程故障数据的系统使用受到一定的限制；同时，在实际应用中受限于复杂度的影响，也只是设置2～3个隐层，降低了逼近的精度；进一步，如何确保故障样本的完整性和典型性以及该方法的收敛性、训练速度和诊断的实时性等，都是制约基于神经网络的微小故障诊断技术发展的瓶颈.

1.3.2支持向量机法

支持向量机（Support vector machine，SVM）是建立在统计学习理论和结构风险最小原理基础上的机器学习算法，最早由Cortes等［95］提出.与神经网络需要大量的训练样本不同，SVM更适合于小样本系统的故障特征的学习和诊断.基于SVM的微小故障诊断通过对特定训练样本的学习达到无错误地识别任意故障类型，适用范围较广.文献［96］综述了SVM在机器状态监控和故障诊断中的应用；针对不同类型故障的样本数目不平衡的问题，文献［97］利用自举法进行样本补偿，然后经过对数变换生成附加的分类特征，提出了最小二乘SVM混合分类器，在对分类器进行训练的过程中，采用粒子群优化算法优化SVM的参数，实现对油浸式电力变压器的溶解气体分析的微小故障检测；在基于SVM的故障诊断中，通常为了单独定义故障标签而采用离散的决策函数，以得到离散的输出值，但是微小故障随着时间的演变较为平缓，离散的决策函数不能充分反映这一演变过程和故障发生的严重性程度，文献［98］为SVM分类器设计了新的连续性决策函数，不仅能辨识故障的类型，而且能监控故障的严重性程度；由于SVM不能直接实现对故障的定位，文献［99］首先利用“一对多”的SVM检测故障是否发生，然后根据带通滤波器和Hilbert变换得到原始信号的包络谱，以此确定故障的发生源.

基于SVM的微小故障检测技术在解决小样本、非线性及高维的故障模式识别中表现出许多优势，但是不足之处是诊断精度与故障样本的完备性和代表性有很大关系.SVM虽然具有较好的学习能力，却也只是从分类的角度对故障进行诊断，并没有深层次地追求数据的结构信息.

1.3.3极限学习机法

极限学习机（Extreme learning machine，ELM）法是黄广斌在2006年提出的一种简单易用、有效的单隐层前馈神经网络学习方法［100］.ELM法只需要对网络的隐层节点个数进行预设置，在执行过程中不需要调整或者修正网络的输入权值以及隐单元的偏置项，具有学习速度快、最优解唯一且泛化性能好的优点，因而也广泛应用于故障诊断领域.鉴于ELM的学习速度优于传统的基于梯度的学习算法，文献［101］采用多层ELM级联作为聚类机制实现液压管的故障诊断；文献［11］充分利用ELM法学习速率快的优势，实现对燃气涡轮发电机系统的实时检测；局部均值分解作为自适应的时频分析方法，适用于非线性、非平稳振动信号的分解，文献［102］提出了结合奇异值分解和ELM算法的滚动轴承微小故障诊断技术.

关于ELM法的研究，目前尚在发展阶段.从几何意义上讲，特别是从函数逼近论的角度分析，ELM法采用的是点点逼近的一阶多项式逼近模式，没有有效表征逼近的光滑性程度，故难以得到相邻点间信号特征的线性组合，因而基于ELM法进行微小故障诊断时会忽视信号相邻点之间的相关性信息.

1.3.4模糊逻辑法

模糊逻辑（Fuzzy logic）法最早由Zadeh于1965年提出［103］，是建立在多值逻辑的基础上，借助于q对模型未知或不确定系统进行推理.基于模糊逻辑的微小故障诊断思想是根据集合论中的隶属函数和模糊关系矩阵建立故障与征兆之间的不确定关系，进而实现故障的检测与诊断.文献［104］详述了这一诊断原理.鉴于ANN法可解释性较差，而模糊逻辑法计算简单、应用方便、结论明确直观，文献［105］将ANN与模糊逻辑相结合实现对电机微小故障的诊断；文献［106］利用小波分析对振动信号进行特征变换，然后结合自适应的模糊推理神经网络，在载荷变动的环境下实现对滚动轴承微小故障的诊断；针对感应电机的微小故障，文献［107］采用决策树方法进行相关特征的选取，结合反向传播算法和最小二乘算法微调自适应的模糊推理神经网络的网络参数.

在模糊故障诊断中，既不需要获取模型中的复杂关系，也不需要得到精确的诊断模型，能够从定性分析的角度处理不完备的数据信息，但由于隶属函数是人为构造的，具有一定的主观因素，同时由于微小故障幅值较小等特点，对故障特征的选择如果不合理，诊断精度会明显下降，因而在诊断微小故障时，一般将该方法与其他智能算法相结合以期获得更好的应用效果.

2　复杂系统的微小故障诊断研究中现存问题

微小故障在检测时的突出难点是容易受到噪声干扰或覆盖，由上文可以看出，尽管有一些改进方法可以降低或消除噪声干扰的影响，但也各有其局限性.目前，国内外关于微小故障诊断方法的研究大都集中体现在针对特定研究对象的具体方法，例如电力电压器、滚动轴承、感应电机等，对于如何设计普适高效的非线性微小故障诊断方法仍将是本领域需长期努力的重点.

2.1系统未知干扰和噪声影响下的微小故障诊断

微小故障信号的显著特点是幅值较低，容易被未知扰动和噪声信号掩盖，特别是当噪声和微小故障特征的模式发生混叠时，很难对其进行区别.

目前，在大多数针对微小故障诊断技术的研究中，考虑到的干扰和噪声基本上为随机白噪声.事实上，许多干扰并非简单的随机性干扰，例如复杂系统中传感器的时滞干扰.当时滞类型不同时，微小故障的显性不同，尤其是时变时滞时，关于故障特性的提取更加困难.同时，由于传感器的感知信息常具有多样的不确定性，提取的特征信息也将具有不同程度的不确定性.当不能够准确判断噪声类型并有效排除干扰信息时，对于微小故障的诊断就容易被忽视或者误判，特别是对于随时间推移具有时隐时现特点的间歇型微小故障，很容易被视为干扰，或者和干扰相混淆叠加.因此如何挖掘并利用更多的隐含信息将微小故障特征与未知扰动和噪声相解耦是亟待解决的问题之一，即在未知扰动和噪声影响下，如何准确且及时地诊断出系统中的微小故障需要更多更深入的理论和工程的研究，特别是对于复杂不确定性系统中微小故障的诊断.

2.2闭环控制下的微小故障诊断

近年来，闭环反馈对动态系统故障诊断的影响得到了进一步关注.正如故障诊断领域著名专家Patton所述，无论实际系统是以开环还是闭环方式运行，现有大部分故障诊断方法本质上都假定系统是以开环状态运行.然而最近一些研究发现，许多原本适用于开环系统的故障诊断方法并不能直接应用于实际闭环系统.文献［108］在对闭环系统故障诊断技术综述的基础上，通过对三容水箱的仿真实验验证了闭环反馈使一些经典的观测器方法性能下降甚至失效.文献［109］通过数例来验证反馈控制不仅会掩盖闭环系统传感器故障源，也会因显著改变传播故障方向而导致错误的故障定位结果.进一步分析发现，当系统为线性标称时，常规故障诊断方法能实现控制输入与残差的完全解耦，此时开环和闭环系统故障诊断方法是等效的；而当系统呈现非线性时，控制输入将无法与残差完全解耦，而且故障经闭环反馈后影响控制信号，进而传播至可控的系统状态和输出变量，这些变量由于系统结构不确定也会作用于残差，从而导致对故障的误诊断.

闭环反馈具有抑制系统性能下降的能力，同时反馈控制的补偿效果也会使得系统的闭环性能对故障具有一定的容错性，因此如何建立故障信号与反馈控制之间的关系是有效实施故障诊断技术的关键性问题.针对微小故障，闭环反馈能充分掩盖其对系统的影响，导致难以及时诊断出故障，故亟待分析系统执行器、传感器和元部件等对输入控制信号的影响机理，深入探究如何融合利用潜在的故障信息以降低反馈控制对随机信号的影响，建立基于反馈控制器的微小故障可诊断性条件，发展适用于闭环系统的微小故障诊断方法.

2.3大数据环境下的微小故障诊断

在数字化的时代背景下，伴随云计算等技术发展，基于数据驱动的故障诊断受到越来越多的关注.如何有效地存储复杂系统的海量数据，并发展和优化数据预处理技术，将直接影响诊断中对故障诊断方法的选取，成为这一研究领域的首要问题.

目前，基于数据驱动的故障诊断，包括微小故障诊断，主要是依赖大量的历史数据.虽然历史数据蕴含了复杂系统大量的运行机理和规律，但在线采样数据更能反映系统当前运行状态中的最新变化，因而有待进一步研究对在线数据的分析处理技术，实现复杂系统故障的在线诊断决策.将故障视为从数据中提取的特征，微小故障诊断就可看作是微小特征识别的问题.对此，现有的机器学习方法都是从逼近论的角度拟合监测数据并表示故障特征，存在计算复杂度和逼近精度等方面的不足，因此如何利用大数据分析工具实现对海量故障数据的快速分析和深度挖掘是大数据时代的挑战性难点.另外，针对不同的大型复杂系统，有待根据其具体运行特点开发特定的基于数据驱动的微小故障诊断系统，真正使研究与实际的工业工程化应用相结合.

2.4多技术融合的微小故障诊断

大型复杂工业系统运行过程中的故障往往具有复杂性、不确定性和多故障并发性等，若只采用单一的故障诊断技术，就会存在精度不高、泛化能力弱等问题，难以获得满意的诊断效果，因而可以利用统计分析、信号处理、人工智能等不同技术之间的差异性和互补性，扬长避短，并结合特征提取和模式识别等方法，提出更为有效的多技术融合微小故障诊断技术，有效提高微小故障诊断系统的敏感性、鲁棒性和精确性，同时降低其不确定性，以便对故障源进行准确定位并估计故障发生的严重程度.

3　基于数据驱动的微小故障诊断研究展望

在故障可诊断的前提下，如何尽早地检测出微小故障始终是故障诊断领域的难点和热点.当现有方法，特别是基于数据驱动的诊断方法，对微小故障的诊断效果不明显时，有三种途径可供参考：1）增加系统中可供诊断的信息量，如对系统增加局部传感器监测得到新的有效故障数据；2）深度挖掘现有信息中的隐含有用信息，如对现有监测数据进行相关性分析、对故障特征向高维空间映射等；3）采用新的更强有力的数学工具.

3.1基于多源信息融合的微小故障诊断展望

基于信号处理的故障诊断方法能依据不确定性的信息进行推理，回避了对研究对象抽取精确数学模型的难点.此类方法往往都是根据系统运行过程中的某一种信息进行观测和分析，进而提取运行状态中故障的征兆.虽然可以判断出故障的发生，但在某些情况下其诊断结果并不可靠.例如对变速箱故障的诊断，如果只利用振动信号的加速度信息进行诊断，得出的结果即便准确，也很难令人信服.因而，需要发展多源信息融合类的故障诊断技术，通过增加新的信息来降低或抑制随机干扰的影响，以提高诊断的准确性、可靠性和有效性.

信息融合是对一个或者多个信息源获取的不同类型的数据和信息进行关联性分析、相关性评价和综合处理，以完成所需的决策和估计任务而进行的信息处理过程.按照融合信息的不同层面可以分为数据层融合、特征层融合和决策层融合.基于信号融合的微小故障诊断的思想是通过利用不同传感器信息之间的互补和冗余关系，对多个信息源加以分析和综合，推算出精确的故障源位置，并对故障发展状态和威胁性重要程度进行全面、及时地评估.

在闭环控制系统中，系统所发生的故障经由反馈回路会使控制律发生改变，甚至经由耦合回路导致其他传感器和执行机构呈现出故障或伪故障现象，也就是说控制信号因闭环反馈而受故障影响.因此，待检测的微小故障信息不仅包含在输出信号中，同时也包含在因闭环反馈而受故障影响的控制信号中.那么针对闭环系统，如何建立故障信号与系统反馈控制之间的关系，充分挖掘并有效整合这些信息以降低随机信号的干扰，是提高故障诊断精度和微小故障可诊断性的一条重要途径.基于此，我们提出融合输出残差信号与反馈控制信号的微小故障诊断思想：利用输出残差信号与反馈控制信号之间的互补性增加待诊断微小故障的显性信息量，并根据它们之间的冗余性提高对微小故障的辨识精度.实验已初步验证了这一想法对微小故障诊断的可行性［110］. 3.2基于关联性分析的微小故障诊断展望

目前，基于多元统计分析的微小故障诊断研究大多采用点点决策的思想，但是单纯依靠复杂系统的输出数据只能反映系统的瞬时特性，无法反映其动态规律，忽视了大数据环境下数据的关联性.不同时刻的随机噪声是相互独立的，或随时间的增加其关联性迅速衰减，否则其中就可能包含故障信息.虽然能量积累可在一定程度上抑制噪声，提高微小故障的检测效果，但若能在诊断中再利用传统方法没有利用到的隐含关联性信息，就有望进一步提高诊断效果.

控制系统中，无论是系统状态发生故障，还是执行器、传感器等发生了故障，都会在输出信息中得到体现.考虑到现有的故障诊断方法仅依赖于当前时刻的系统输出信号或输出残差，这是微小故障在各种干扰作用下常被漏检的主要原因之一.当前残差信息不仅包含前一时刻至当前时刻的新增信息及未建模信息，而且包含之前时刻残差信息中未被检测出的微小故障信息等.因而，考虑如何有效地利用多相邻时刻残差信息序列中微小故障特征的相关性来检测微小故障，将是一种有利于降低漏检率的新思想.故此，我们提出基于残差信号相关性分析的微小故障诊断思想：基于已发生的故障所具有的持续性，借鉴目标跟踪领域检测前对疑似目标跟踪的航迹关联思想，通过设计疑似故障检测的较小阈值，利用在一定时段内被检测疑似故障的多样性和时隐时现性，建立相邻时刻疑似故障的相似或相关性，构造由疑似故障形成的故障航迹，并据此进行非线性的动态航迹诊断.其难点在于如何设计适宜的疑似故障检测阈值及如何形成有效故障航迹，过大则将错失检测出微小故障，过小又会因疑似故障过多而难以形成用于有效诊断的航迹.理论上，基于多元统计分析的方法若能将点点决策与关联性分析相结合，有望提高微小故障的诊断效果.

3.3基于机器学习的微小故障诊断展望

传统的智能学习方法，无论是用于分类还是回归，多数为浅层结构算法，其局限性在于有限样本和计算单元情况下对复杂函数的表示能力有限，针对复杂分类问题其泛化能力受到一定制约.如何从监测数据中对故障特征进行挖掘并表示是基于数据驱动的故障诊断类方法较为关键的一步，如果能利用更多改进的算法对传统方法没有表征出的故障特征信息进行合理提取并表征，就能得到更好的故障检测和预测结果.依据函数逼迫论的思想，从理论上讲，如果能对特征提取得足够完备，即能采用精度足够高的高阶多项式对故障特征进行表示，并刻画出数据中隐含的细节性信息，就能检测出系统中的潜在微小故障.

考虑到目前用于故障诊断领域的机器学习方法，例如神经网络、支撑向量机等，尚不能够充分挖掘监测数据中的故障特征，特别是微小的故障特征，我们提出基于特征完美表示的微小故障诊断思想：故障诊断依赖于从获取信息中对特征信息提取的完备性和精度，同时也依赖于对提取特征信息的完美程度；利用近年来已在模式识别领域成为微小特征提取热点的深度学习、Spark、Hadoop等大数据分析工具以及稀疏表示的思想和方法，用于微小故障的检测与诊断，期望取得新的突破.

深度学习方法通过设置网络层中隐单元的个数来实现对数据所有变量间信息的统计，包括数据结构和分布式特征.同时，深度学习通过设置多层的神经网络实现对特征多层次的提取，深度挖掘出数据的微小特征.因此，理论上如果能基于深度学习实现对故障信息的提取，再选取合适的分类器，就能从本质上做到对故障诊断性能的提升.基于深度学习的故障诊断方法的技术难点在于网络的层数和每层的节点数的设置，这不仅决定着对特征信息提取完备性和表示完美性，同时与计算复杂度密切相关；而对故障检测和分类精度则依赖于如何设计准确而灵巧的分类器.相对于传统的多元统计算法，深度学习减少了数据隐含信息的丢失，同时对于传统的人工智能算法，深度学习更深层次地追求数据的本质特性和结构信息.对此，我们已通过实验初步验证了利用深度学习能提高微小故障的诊断能力，并且可以不依赖测试变量的历史数据，达到实时在线诊断目的，这对工业系统中故障的检测具有较强的实用意义［111］.

3.4基于时频分析的微小故障诊断展望

基于时频分析的故障诊断都是将监测到的原始状态信号，也就是原本难以处理的时域信号，转换成易于分析的频域信号，进而依据振幅、频率和相位等信息进行分析，得到故障征兆.傅里叶变换可以实现信号在时域和频域的相互转换，但不能给出频率分量的时变信息，因而只适用于平稳信号的分析.鉴于此，针对非平稳信号提出了稀疏表示的思想［112-113］.不同于传统的时频表示，稀疏表示的分解集是过完备的原子字典，可以构造具有较好时频聚集性的时频分布，有效揭示信号的内在结构.另一方面，由于从时域到频域的直接映射会导致信号的瞬时频率等特征的丢失，不能完全展示故障信号的逐步变化过程.而分数阶傅里叶变换作为传统傅里叶变换的分数幂形式，可以将相对独立的时域和频域联系起来，从整体上展示信号的频率成分，适于分析确定性信号和平稳信号，同时对于非平稳信号，它能够将其映射为二维时频平面以进行时频分析，全面反映信号随时间变化的频率分布特征［114-116］.

此外，稀疏表示和分数阶傅里叶变换都是线性变换，没有交叉项干扰，在具有加性噪声的多分量情况下更具优势.目前，基于稀疏表示和分数阶傅里叶变换等进行故障诊断已有部分研究［117］，主要侧重对非平稳信号进行局部化时频分析，但是针对微小故障诊断方面仍未充分发挥其优势，有待进一步探究.

4　结束语

故障诊断是降低事故风险率的一个行之有效的重要方法.本文从数据驱动的角度对微小故障的常用诊断方法进行回顾，将现有的诊断方法分为基于统计分析的方法、基于信号处理的方法和基于人工智能的方法，并指出了各类方法的适用性和局限性.最后指出复杂系统微小故障研究中的现存问题，并从增加新的信息、挖掘未利用的隐含信息和采用新的数学工具三个角度对这一领域进行展望，提出了基于关联性分析、基于多源信息融合、基于机器学习、基于时频分析这四个值得探究的微小故障诊断思想.当然，由于微小与显著是相对而言的，对于非线性系统或对动态系统特性不完全了解的微小故障诊断问题，还需要更多更深入的研究.

References

1 Himmelblau D M.Fault Detection and Diagnosis in Chemi

cal and Petrochemical Processes.New York：Elsevier，1978.

2 Ren L，Xu Z Y，Yan X Q.Single-sensor incipient fault detection.IEEE Sensors Journal，2011，11（9）：2102-2107

3 Amar M，Gondal I，Wilson C.Vibration spectrum imaging：a novel bearing fault classification approach.IEEE Transactions on Industrial Electronics，2015，62（1）：494-502

4 Li B，Chow M Y，Tipsuwan Y，Hung J C.Neural-networkbased motor rolling bearing fault diagnosis.IEEE Transactions on Industrial Electronics，2000，47（5）：1060-1069

5 Demetriou M A，Polycarpou M M.Incipient fault diagnosis of dynamical systems using online approximators.IEEE Transactions on Automatic Control，1998，43（11）：1612-1617

6 Naderi M S，Gharehpetian G B，Abedi M，Blackburn T R.Modeling and detection of transformer internal incipient fault during impulse test.IEEE Transactions on Dielectrics and Electrical Insulation，2008，15（1）：284-291

7 Oda T，Katoh E.Fault Diagnosis Expert System，U.S. Patent 5127005，June 1992.

8 Yan R Q，Gao R X，Chen X F.Wavelets for fault diagnosis of rotary machines：a review with applications.Signal Processing，2014，96：1-15

9 Chiang L H，Russell E L，Braatz R D.Fault diagnosis in chemical processes using Fisher discriminant analysis，discriminant partial least squares，and principal component analysis.Chemometrics and Intelligent Laboratory Systems，2000，50（2）：243-252

10 Yoon S，MacGregor J F.Fault diagnosis with multivariate statistical models，part I：using steady state fault signatures. Journal of Process Control，2001，11（4）：387-400

11 Wong P K，Yang Z X，Vong C M，Zhong J H.Real-time fault diagnosis for gas turbine generator systems using extreme learning machine.Neurocomputing，2014，128：249-257

12 Li K，Zhang Y L，Li Z X.Application research of Kalman filter and SVM applied to condition monitoring and fault diagnosis.Applied Mechanics and Materials，2012，121-126：268-272

13 Li Juan，Zhou Dong-Hua，Si Xiao-Sheng，Chen Mao-Yin，Xu Chun-Hong.Review of incipient fault diagnosis methods. Control Theory and Applications，2012，29（12）：1517-1529（李娟，周东华，司小胜，陈茂银，徐春红.微小故障诊断方法综述.控制理论与应用，2012，29（12）：1517-1529）

14 Ren W，Beard R W.Consensus algorithms for doubleintegrator dynamics.Distributed Consensus in Multi-vehicle Cooperative Control：Theory and Application.London：Springer，2008.77-104

15 Venkatasubramanian V，Rengaswamy R，Yin K，Kavuri S N.A review of process fault detection and diagnosis：Part I：quantitative model-based methods.Computers and Chemical Engineering，2003，27（3）：293-311

16 Li Han，Xiao De-Yun.Survey on data driven fault diagnosis methods.Control and Decision，2011，26（1）：1-9（李晗，萧德云.基于数据驱动的故障诊断方法综述.控制与决策，2011，26（1）：1-9）

17 Pearson K.Principal components analysis.The London，Edinburgh，and Dublin Philosophical Magazine and Journal of Science，1901，6（2）：559

18 Bartlett M S.Multivariate analysis.Supplement to the Journal of the Royal Statistical Society，1947，9（2）：176-197

19 Wiesel A，Hero A O.Decomposable principal component analysis.IEEE Transactions on Signal Processing，2009，57（11）：4369-4377

20 Wise B M，Ricker N L，Veltkamp D F，Kowalski B R.A theoretical basis for the use of principal component models for monitoring multivariate processes.Process Control and Quality，1990，1（1）：41-51

21 Kaistha N，Upadhyaya B R.Incipient fault detection and isolation in a PWR plant using principal component analysis.In：Proceedings of the 2001 American Control Conference.Arlington，VA，USA：IEEE，2001.2119-2120

22 Zhao J S，Huang J C，Sun W.On-line early fault detection and diagnosis of municipal solid waste incinerators.Waste Management，2008，28（11）：2406-2414

23 Ge Zhi-Qiang，Yang Chun-Jie，Song Zhi-Huan.Research and application of small shifts detection method based on MEWMA-PCA.Information and Control，2007，36（5）：650-656（葛志强，杨春节，宋执环.基于MEWMA-PCA的微小故障检测方法研究及其应用.信息与控制，2007，36（5）：650-656）

24 Wen Cheng-Lin，Hu Jing，Wang Tian-Zhen，Chen Zhi-Guo. Relative PCA with applications of data compression and fault diagnosis.Acta Automatica Sinica，2008，34（9）：1128-1139（文成林，胡静，王天真，陈志国.相对主元分析及其在数据压缩和故障诊断中的应用研究.自动化学报，2008，34（9）：1128-1139）

25 Zhou F N，Tang T H，Wen C L.DCA based multi-level small fault diagnosis.In：Proceedings of the 11th IEEE International Conference on Communication Technology. Hangzhou，China：IEEE，2008.486-489

26 Harmouche J，Delpha C，Diallo D.Incipient fault detection and diagnosis based on Kullback-Leibler divergence using principal component analysis：Part I.Signal Processing，2014，94：278-287

27 Harmouche J，Delpha C，Diallo D.Incipient fault detection and diagnosis based on Kullback-Leibler divergence using principal component analysis：Part II.Signal Processing，2015，109：334-344

28 Comon P.Independent component analysis.Higher-Order Statistics.Amsterdam：Elsevier，1992.29-38

29 Kano M，Tanaka S，Hasebe S，Hashimoto I，Ohno H.Monitoring independent components for fault detection.AIChE Journal，2003，49（4）：969-976

30 Ge Z Q，Song Z H.Process monitoring based on independent component analysis—principal component analysis（ICA-PCA）and similarity factors.Industrial and Engineering Chemistry Research，2007，46（7）：2054-2063

31 Tian X H，Lin J，Fyfe K R，Zuo M J.Gearbox fault diagnosis using independent component analysis in the frequency domain and wavelet filtering.In：Proceedings of the 2003 IEEE International Conference on Acoustics，Speech，and Signal Processing.Hong Kong，China：IEEE，2003.II-245-II-248 32 He Q B，Du R X，Kong F R.Phase space feature based on independent component analysis for machine health diagnosis.Journal of Vibration and Acoustics，2012，134（2）：021014

33 Ge Z Q，Xie L，Kruger U，Song Z H.Local ICA for multivariate statistical fault diagnosis in systems with unknown signal and error distributions.AIChE Journal，2012，58（8）：2357-2372

34 Guo Y，Wu X，Na J，Fung R F.Incipient faults identification in gearbox by combining Kurtogram and independent component analysis.Applied Mechanics and Materials，2015，764-765：309-313

35 Abdi H.Partial least square regression.Encyclopedia for Research Methods for the Social Sciences.Thousand Oaks：Sage，2003.792-795

36 Kresta J V，Macgregor J F，Marlin T E.Multivariate statistical monitoring of process operating performance.Canadian Journal of Chemical Engineering，1991，69（1）：35-47

37 Vigneau E，Bertrand D，Qannari E M.Application of latent root regression for calibration in near-infrared spectroscopy. Comparison with principal component regression and partial least squares.Chemometrics and Intelligent Laboratory Systems，1996，35（2）：231-238

38 Komulainen T，Sourander M，J¨ams¨a-Jounela S L.An online application of dynamic PLS to a dearomatization process. Computers and Chemical Engineering，2004，28（12）：2611-2619

39 Qin S J，Zheng Y Y.Quality-relevant and process-relevant fault monitoring with concurrent projection to latent structures.AIChE Journal，2013，59（2）：496-504

40 Kruger U，Dimitriadis G.Diagnosis of process faults in chemical systems using a local partial least squares approach.AIChE Journal，2008，54（10）：2581-2596

41 Zhang X D，Polycarpou M M，Parisini T.Fault diagnosis of a class of nonlinear uncertain systems with Lipschitz nonlinearities using adaptive estimation.Automatica，2010，46（2）：290-299

42 Harmouche J，Delpha C，Diallo D.Incipient fault amplitude estimation using KL divergence with a probabilistic approach.Signal Processing，2016，120：1-7

43 Lee D D，Seung H S.Learning the parts of objects by nonnegative matrix factorization.Nature，1999，401（6755）：788 -791

44 Hoyer P O.Non-negative sparse coding.In：Proceedings of the 12th IEEE Workshop on Neural Networks for Signal Processing.Martigny，Switzerland：IEEE，2002.557-565

45 Tangirala A K，Kanodia J，Shah S L.Non-negative matrix factorization for detection and diagnosis of plantwide oscillations.Industrial and Engineering Chemistry Research，2007，46（3）：801-817

46 Wang Q H，Zhang Y Y，Cai L，Zhu Y S.Fault diagnosis for diesel valve trains based on non-negative matrix factorization and neural network ensemble.Mechanical Systems and Signal Processing，2009，23（5）：1683-1695

47 Li B，Zhang P L，Liu D S，Mi S S，Ren G Q，Tian H.Feature extraction for rolling element bearing fault diagnosis utilizing generalized S transform and two-dimensional nonnegative matrix factorization.Journal of Sound and Vibration，2011，330（10）：2388-2399

48 Kirchg¨assner G，Wolters J.Introduction to Modern Time Series Analysis.Berlin Heidelberg：Springer，2007.2-5

49 Cong F Y，Chen J，Dong G M，Zhao F G.Short-time matrix series based singular value decomposition for rolling bearing fault diagnosis.Mechanical Systems and Signal Processing，2013，34（1-2）：218-230

50 Menon S，Uluyol¨O，Kim K，Nwadiogbu E O.Incipient fault detection and diagnosis in turbine engines using hidden Markov models.In：Proceedings of the 2003 ASME Turbo Expo，Collocated with the 2003 International Joint Power Generation Conference.Arlington，Georgia，USA：ASME，2003.493-500

51 Purushotham V，Narayanan S，Prasad S A N.Multi-fault diagnosis of rolling bearing elements using wavelet analysis and hidden Markov model based fault recognition.NDT and E International，2005，38（8）：654-664

52 Li Z F，Fang H J，Xia L S.Increasing mapping based hidden Markov model for dynamic process monitoring and diagnosis.Expert Systems with Applications，2014，41（2）：744-751

53 Bhatnagar S，Rajagopalan V，Ray A.Incipient fault detection in mechanical power transmission systems.In：Proceedings of the 2005 American Control Conference.Portland，OR：IEEE，2005.472-477

54 D＇Angelo M F S V，Palhares R M，Takahashi R H C，Loschi R H，Baccarini L M R，Caminhas W M.Incipient fault detection in induction machine stator-winding using a fuzzy-Bayesian change point detection approach.Applied Soft Computing，2011，11（1）：179-192

55 Barman D，Sarkar S，Das G，Das S，Purkait P.DFA and DWT based severity detection and discrimination of induction motor stator winding short circuit fault from incipient insulation failure.In：Proceedings of the 2015 International Conference on Electrical，Electronics，Signals，Communication，and Optimization.Visakhapatnam：IEEE，2015.1-6

56 Liu H C，Liu L，Bian Q H，Lin Q L，Dong N，Xu P C.Failure mode and effects analysis using fuzzy evidential reasoning approach and grey theory.Expert Systems with Applications，2011，38（4）：4403-4415

57 Wang M H.Grey-extension method for incipient fault forecasting of oil-immersed power transformer.Electric Power Components and Systems，2004，32（10）：959-975

58 Lin C H，Chen J L，Huang P Z.Dissolved gases forecast to enhance oil-immersed transformer fault diagnosis with grey prediction-clustering analysis.Expert Systems，2011，28（2）：123-137

59 Wang M H，Tsai H H.Fuel cell fault forecasting system using grey and extension theories.IET Renewable Power Generation，2012，6（6）：373-380

60 Qiao W，Lu D G.A survey on wind turbine condition monitoring and fault diagnosis—part II：signals and signal processing methods.IEEE Transactions on Industrial Electronics，2015，62（10）：6546-6557

61 Daubechies I.Ten Lectures on Wavelets.Philadelphia：Society for Industrial and Applied Mathematics，1992.

62 Rubini R，Meneghetti U.Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearings.Mechanical Systems and Signal Processing，2001，15（2）：287-302

63 Saravanan N，Ramachandran K I.Incipient gear box fault diagnosis using discrete wavelet transform（DWT）for feature extraction and classification using artificial neural network（ANN）.Expert Systems with Applications，2010，37（6）：4168-4181

64 Sun W，Yang G A，Chen Q，Palazoglu A，Feng K.Fault diagnosis of rolling bearing based on wavelet transform and envelope spectrum correlation.Journal of Vibration and Control，2013，19（6）：924-941

65 Luo Rong，Tian Fu-Qing，Li Ke-Yu，Ding Qing-Xi.Realization of convolution wavelet transformation and its application in mechanical incipient fault diagnosis.Journal of Vibration and Shock，2013，32（7）：64-69（罗荣，田福庆，李克玉，丁庆喜.卷积型小波变换实现及机械早期故障诊断应用.振动与冲击，2013，32（7）：64-69）

66 Sugumaran V，Rao A V，Ramachandran K I.A comprehensive study of fault diagnostics of roller bearings using continuous wavelet transform.International Journal of Manufacturing Systems and Design，2015，1（1）：27-46

67 Kay S M，Marple S L Jr.Spectrum analysis—a modern perspective.Proceedings of the IEEE，1981，69（11）：1380-1419

68 Feng Z P，Chen X W，Liang M.Joint envelope and frequency order spectrum analysis based on iterative generalized demodulation for planetary gearbox fault diagnosis under nonstationary conditions.Mechanical Systems and Signal Processing，2016，76-77：242-264

69 Drago R J.Incipient failure detection.Power Transmission Design，1979，21（2）：40-45

70 Nandi S，Toliyat H A，Li X.Condition monitoring and fault diagnosis of electrical motors—a review.IEEE Transactions on Energy Conversion，2005，20（4）：719-729

71 Oh J E，Kim W T，Sim H J，Lee J Y.Advanced multidimensional spectral analysis and its application for early fault detection.Proceedings of the Institution of Mechanical Engineers，Part D：Journal of Automobile Engineering，2006，220（4）：435-444

72 Muruganatham B，Sanjith M A，Krishnakumar B，Satya Murty S A V.Roller element bearing fault diagnosis using singular spectrum analysis.Mechanical Systems and Signal Processing，2013，35（1-2）：150-166

73 Xie S L，Zhang Y H，Xie Q，Chen C H，Zhang X N.Identification of high frequency loads using statistical energy analysis method.Mechanical Systems and Signal Processing，2013，35（1-2）：291-306

74 Elsner J B，Tsonis A A.Singular Spectrum Analysis：A New Tool in Time Series Analysis.New York：Springer Science &Business Media，1996.

75 Huang N E，Shen Z，Long S R，Wu M C，Shi H H，Zheng Q A，Yen N C，Tung C C，Liu H H.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis.Proceedings of the Royal Society of London A：Mathematical，Physical and Engineering Sciences，1998，454（1971）：903-995

76 Flandrin P，Rilling G，Goncalves P.Empirical mode decomposition as a filter bank.IEEE Signal Processing Letters，2004，11（2）：112-114

77 Elbouchikhi E，Choqueuse V，Trachi Y，Benbouzid M.Induction machine bearing faults detection based on Hilbert-Huang transform.In：Proceedings of the 24th IEEE International Symposium on Industrial Electronics.Buzios：IEEE，2015.843-848

78 Liang J，Yang Z X.A novel wavelet transform—empirical mode decomposition based sample entropy and SVD approach for acoustic signal fault diagnosis.In：Proceedings of the 6th International Conference on Advances in Swarm and Computational Intelligence.Beijing，China：Springer International Publishing，2015.232-241

79 Yan J H，Lu L.Improved Hilbert-Huang transform based weak signal detection methodology and its application on incipient fault diagnosis and ECG signal analysis.Signal Processing，2014，98：74-87

80 Lei Y G，Lin J，He Z J，Zuo M J.A review on empirical mode decomposition in fault diagnosis of rotating machinery.Mechanical Systems and Signal Processing，2013，35（1-2）：108-126

81 Giardina C R，Dougherty E R.Morphological Methods in Image and Signal Processing.Englewood Cliffs：Prentice Hall，1988.

82 Zhang L J，Xu J W，Yang J H，Yang D B，Wang D D. Multiscale morphology analysis and its application to fault diagnosis.Mechanical Systems and Signal Processing，2008，22（3）：597-610

83 He W，Jiang Z N，Qin Q.A joint adaptive wavelet filter and morphological signal processing method for weak mechanical impulse extraction.Journal of Mechanical Science and Technology，2010，24（8）：1709-1716

84 Dong Y B，Liao M F，Zhang X L，Wang F Z.Faults diagnosis of rolling element bearings based on modified morphological method.Mechanical Systems and Signal Processing，2011，25（4）：1276-1286

85 Li B，Zhang P L，Wang Z J，Mi S S，Zhang Y T.Gear fault detection using multi-scale morphological filters.Measurement，2011，44（10）：2078-2089

86 Li B，Zhang P L，Wang Z J，Mi S S，Liu D S.A weighted multi-scale morphological gradient filter for rolling element bearing fault detection.ISA Transactions，2011，50（4）：599 -608

87 McCulloch W S，Pitts W.A logical calculus of the ideas immanent in nervous activity.The Bulletin of Mathematical Biophysics，1943，5（4）：115-133

88 Watanabe K，Matsuura I，Abe M，Kubota M，Himmelblau D M.Incipient fault diagnosis of chemical processes via artificial neural networks.AIChE Journal，1989，35（11）：1803-1812

89 Chow M Y，Mangum P，Thomas R J.Incipient fault detection in DC machines using a neural network.In：Proceedings of the 22nd Asilomar Conference on Signals，Systems，and Computers.Pacific Grove，CA：IEEE，1988.706-709

90 Zakaria F，Johari D，Musirin I.Artificial neural network（ANN）application in dissolved gas analysis（DGA）methods for the detection of incipient faults in oil-filled power transformer.In：Proceedings of the 2012 IEEE International Conference on Control System，Computing，and Engineering.Penang，Malaysia：IEEE，2012.328-332

91 Bhalla D，Bansal R K，Gupta H O.Function analysis based rule extraction from artificial neural networks for transformer incipient fault diagnosis.International Journal of Electrical Power and Energy Systems，2012，43（1）：1196-1203

92 Bhowmik P S，Pradhan S，Prakash M，Roy S.Investigation of wavelets and radial basis function neural network for incipient fault diagnosis in induction motors.In：Proceedings of the 2013 International Conference on Circuits，Controls，and Communications.Bengaluru：IEEE，2013.1-5

93 Zhang Z Y，Wang Y，Wang K S.Fault diagnosis and prognosis using wavelet packet decomposition，Fourier transform and artificial neural network.Journal of Intelligent Manufacturing，2013，24（6）：1213-1227

94 Hornik K，Stinchcombe M，White H.Multilayer feed forward networks are universal approximators.Neural Networks，1989，2（5）：359-366

95 Cortes C，Vapnik V.Support-vector networks.Machine Learning，1995，20（3）：273-297

96 Widodo A，Yang B S.Support vector machine in machine condition monitoring and fault diagnosis.Mechanical Systems and Signal Processing，2007，21（6）：2560-2574

97 Wei C H，Tang W H，Wu Q H.A hybrid least-square support vector machine approach to incipient fault detection for oilimmersed power transformer.Electric Power Components and Systems，2014，42（5）：453-463

98 Namdari M，Jazayeri-Rad H.Incipient fault diagnosis using support vector machines based on monitoring continuous decision functions.Engineering Applications of Artificial Intelligence，2014，28：22-35

99 Fern´andez-Francos D，Mart´ınez-Rego D，Fontenla-Romero O，Alonso-Betanzos A.Automatic bearing fault diagnosis based on one-class ν-SVM.Computers and Industrial Engineering，2013，64（1）：357-365

100 Huang G B，Zhu Q Y，Siew C K.Extreme learning machine：theory and applications.Neurocomputing，2006，70（1-3）：489-501

101 Hu X F，Zhao Z，Wang S，Wang F L，He D K，Wu S K. Multi-stage extreme learning machine for fault diagnosis on hydraulic tube tester.Neural Computing and Applications，2008，17（4）：399-403

102 Tian Y，Ma J，Lu C，Wang Z L.Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine.Mechanism and Machine Theory，2015，90：175-186

103 Zadeh L A.Fuzzy sets.Information and Control，1965，8（3）：338-353

104 Isermann R.On fuzzy logic applications for automatic control，supervision，and fault diagnosis.IEEE Transactions on Systems，Man，and Cybernetics，Part A：Systems and Humans，1998，28（2）：221-235

105 Chow M Y.Methodologies of Using Neural Network and Fuzzy Logic Technologies for Motor Incipient Fault Detection.River Edge，NJ，USA：World Scientific，1997.

106 Lou X S，Loparo K A.Bearing fault diagnosis based on wavelet transform and fuzzy inference.Mechanical Systems and Signal Processing，2004，18（5）：1077-1095

107 Yang B S，Oh M S，Tan A C C.Fault diagnosis of induction motor based on decision trees and adaptive neuro-fuzzy inference.Expert Systems with Applications，2009，36（2）：1840-1849

108 Zhou Dong-Hua，Liu Yang，He Xiao.Review on fault diagnosis techniques for closed-loop systems.Acta Automatica Sinica，2013，39（11）：1933-1943（周东华，刘洋，何潇.闭环系统故障诊断技术综述.自动化学报，2013，39（11）：1933-1943）

109 McNabb C A，Qin S J.Fault diagnosis in the feedbackinvariant subspace of closed-loop systems.Industrial and Engineering Chemistry Research，2005，44（8）：2359-2368

110 Gao Jing-Li，Wen Cheng-Lin，Liu Mei-Qin.Low-speed small target detection based on SVD and superposition. Journal of Shanghai Jiaotong University，2015，49（6）：876-883（高敬礼，文成林，刘妹琴.基于奇异值分解和叠加法的慢速小目标检测算法.上海交通大学学报，2015，49（6）：876-883）

111 Lv F Y，Wen C L，Bao Z J，Liu M Q.Fault diagnosis based on deep learning.In：Proceedings of the 2016 American Control Conference（ACC2016），Boston，MA，USA：IEEE，2016.6851-6856

112 Li C L，Hu S Y，Gao S H，Tang J.Real-time grayscalethermal tracking via Laplacian sparse representation.In：Proceedings of the 22nd International Conference on MultiMedia Modeling.Miami，FL，USA：Springer International Publishing，2016.54-65

113 Xu Y，Zhang Z，Lu G M，Yang J.Approximately symmetrical face images for image preprocessing in face recognition and sparse representation based classification.Pattern Recognition，2016，54：68-82

114 Namias V.The fractional order Fourier transform and its application to quantum mechanics.IMA Journal of Applied Mathematics，1980，25（3）：241-265

115 Ozaktas H M，Ankan O，Kutay M A，Bozdagt G.Digital computation of the fractional Fourier transform.IEEE Transactions on Signal Processing，1996，44（9）：2141-2150

116 Gao Zhe，Liao Xiao-Zhong.A stability criterion for linear fractional order systems in frequency domain.Acta Automatica Sinica，2011，37（11）：1387-1394（高哲，廖晓钟.一种线性分数阶系统稳定性的频域判别准则.自动化学报，2011，37（11）：1387-1394）

117 Lin L F，Wang H Q，Lv W Y，Zhong S C.A novel parameter-induced stochastic resonance phenomena in fractional Fourier domain.Mechanical Systems and Signal Processing，2016，76-77：771-779

文成林杭州电子科技大学自动化学院教授.主要研究方向为信息融合，多目标跟踪，故障诊断.本文通信作者.

E-mail：wencl@hdu.edu.cn

（WEN Cheng-LinProfessor at the School of Automation，Hangzhou Dianzi University.His research interest covers information fusion，multi-target tracking，and fault diagnosis.Corresponding author of this paper.）

吕菲亚浙江大学电气工程学院博士研究生.主要研究方向为故障诊断，智能控制，大数据分析.

E-mail：lvfeiya0215@126.com

（LV Fei-YaPh.D.candidate at the College of Electrical Engineering，Zhejiang University.Her research interest covers fault diagnosis，intelligent control，and big data analysis.）

包哲静浙江大学电气工程学院副教授.主要研究方向为智能控制，故障诊断，大数据分析和微电网规划.

E-mail：zjbao@zju.edu.cn

（BAO Zhe-JingAssociate professor at the College of Electrical Engineering，Zhejiang University.Her research interest covers intelligent control，fault diagnosis，big data analysis，and planning of microgrid.）

刘妹琴浙江大学电气工程学院教授.主要研究方向为鲁棒控制，多传感器网络，信息融合.

E-mail：liumeiqin@zju.edu.cn

（LIU Mei-QinProfessor at the College of Electrical Engineering，Zhejiang University.Her research interest covers robust control，multi-sensor networks， and information fusion.）

A Review of Data Driven-based Incipient Fault Diagnosis

WEN Cheng-Lin1LV Fei-Ya2BAO Zhe-Jing2LIU Mei-Qin2

As timely incipient fault diagnosis is the key to guarantee operation safety and suppress fault deterioration，this paper gives a review of data driven-based researches for incipient faults，which have low amplitude and may be covered by system disturbance and noise easily.Data driven-based incipient fault diagnosis can be divided into three parts，i.e.，statistical analysis-based technology，signal processing-based technology，artificial intelligence-based technology.Their basic ideas，research progresses，application and limitations are discussed in detail.Furthermore，this paper not only points out the existing problems about complex systems，but also looks forward to the advance of this area by means of adding new information，mining unused implied information，using new mathematical tools.Finally，four thoughts worth exploring are proposed：diagnosis based on correlation analysis，multi-source information fusion，machine learning and time-frequency transform.

Incipient fault diagnosis，data driven，statistical analysis，signal processing，artificial intelligence

Manuscript February 29，2016；accepted June 6，2016

10.16383/j.aas.2016.c160105

Wen Cheng-Lin，Lv Fei-Ya，Bao Zhe-Jing，Liu Mei-Qin.A review of data driven-based incipient fault diagnosis. Acta Automatica Sinica，2016，42（9）：1285-1299

2016-02-29录用日期2016-06-06

国家自然科学基金（U1509203，61333005，61490701，61273170），浙江省自然科学基金（LZ15F030001）资助

Supported by National Natural Science Foundation of China（U1509203，61333005，61490701，61273170）andZhejiang Provincial Natural Science Foundation of China（LZ15F030001）

本文责任编委高会军

Recommended by Associate Editor GAO Hui-Jun

1.杭州电子科技大学自动化学院杭州3100182.浙江大学电气工程学院杭州310027

1.School of Automation，Hangzhou Dianzi University，Hangzhou 3100182.College of Electrical Engineering，Zhejiang University，Hangzhou 310027