判定正项级数审敛性的一种方法

刘春艳

(山西大同大学数学与计算机科学学院,山西大同037009）

判定正项级数审敛性的一种方法

刘春艳

(山西大同大学数学与计算机科学学院,山西大同037009）

正项级数的敛散性是常数项级数的重点,为了更好判断正项级数的敛散性,给出了正项级数一种新的审敛法。

正项级数;比值审敛法;根值审敛法

正项级数的审敛判断方法有很多种,文中在比较判别法的基础上,将比值审敛法和根值审敛法进行推广得到一种新的判别方法。

则:(1)当r＜1时,级数收敛;

(2)当r＞1时,级数发散;

(3)当r=1时,级数可能收敛也可能发散。

则:(1)当r＜1时,级数收敛;

(2)当r＞1时,级数发散;

(3)当r=1时,级数可能收敛也可能发散。

下面由这两个审敛法及比较审敛法推出以下结论:

定理3设un=wnvn,wn≥0,

vn＞0(n=1,2,3……),

则(1)当wv＜1时,级数收敛;

(2)当wv＞1时,级数发散。

证明(1)当wv＜1时,取适当小的ε＞0,使(w+ε)(v+ε)＜1，

取N=max{n1,n2}，则当n＞N时,(1)(2)同时

因为vm·(w+ε)m为一常数且(w+ε)(v+ε)＜1,所以级数收敛,由比较审敛法知收敛。

(2)当wv＞1时,取适当小的ε＞0,使(w-ε)(v-ε)＞1，

取N=max{n1,n2}，则当n＞N时,(3)(4)同时，

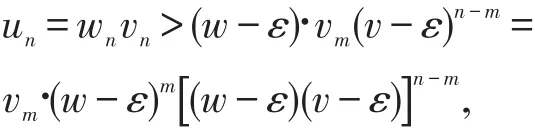
因为vm·(w-ε)m为一常数且(w-ε)(v-ε)＞1,

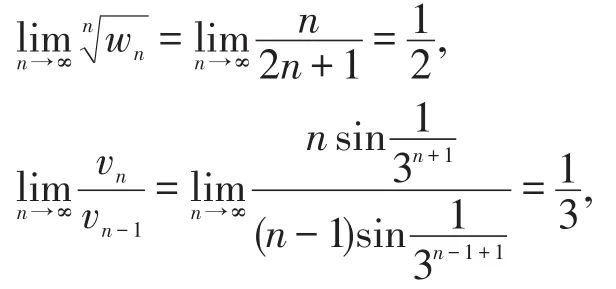
u=wv=,级数收敛。

由级数收敛的必要条件知,级数发散。

[1]杨钟玄.正项级数敛散性的一个判别法[J].四川师范大学学报（自然科学版），2005,28（6）：667-670.

[2]洪勇.一个新的正项级数敛散性判别定理及应用[J].四川师范大学学报（自然科学版），2004,27（3）：245-267.

[3]张永明.正项级数收敛性的一种新的判别法[J].数学的实践与认识,2004,34（1）:173-176.

A Method about Discriminating Convergence and Divergence of Positive Term Series

LIU Chun-yan
(School of Mathematics and Computer Sciences,Shanxi Datong University,Datong Shanxi,037009)

The convergence and divergence of positive series is the key of the constant term series.In order to better determine positive series,a new convergence test of positive series is introduced in this paper.

positive series;ratio criterion;Cauchy root criterion

O173.1

A

1674-0874(2016)05-0012-02

2016-07-16

刘春艳(1965-),女，山西大同人，副教授，研究方向：高等数学。

〔责任编辑 高海〕