工程裂缝扩展对现役混凝土结构受力性能的影响

王海军，　高帅强

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)



工程裂缝扩展对现役混凝土结构受力性能的影响

王海军，高帅强

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)

现役的混凝土构件大多是带裂缝工作，部分裂缝已经超过规范的限值，这些超限裂缝群使现役结构存在安全隐患。根据混凝土断裂力学理论，采用KINH混凝土本构模型，对混凝土裂缝进行奇异性处理，应用降温法对钢筋施加预应力，利用ANSYS有限元软件分析裂缝长度、宽度、深度方向的扩展对箱梁受力性能的影响。结果表明：随着裂缝群尺寸的扩展，混凝土的最大压应力和最大拉应力均增大；最大应力的变化对裂缝群宽度最敏感。根据分析结果,给出裂缝修补与否建议模型，提供了需要修补的合理尺寸范围。

混凝土结构； 裂缝扩展； 拉应力； 压应力

0　引　言

现役混凝土结构的破坏和倒塌大多是从裂缝的扩展开始的。随着混凝土结构(桥梁、建筑、大坝)的大量修建，出现开裂问题的混凝土结构也越来越多[1-4]。国内外学者统计汇总了混凝土结构裂缝的种类、表现形式，并对各类裂缝的成因如预应力损失、超载、混凝土收缩徐变等[5-9]进行了深入的研究，取得了相应的成果，这些研究成果可以为结构的维修和加固方法提供参考。

实际工程中，现役混凝土结构裂缝修补，不仅要考虑其造成的力学结果，还要考虑维修的经济成本。针对现役混凝土结构中存在的裂缝群，甄别裂缝状态，定义裂缝的危险程度，从而给出是否修补的建议，就显得十分重要。笔者依托某现役预应力混凝土箱梁桥，针对开裂相对严重的节段，分析裂缝扩展对节段受力性能的影响，确定危险裂缝的尺寸，进而对裂缝修补与否提出建议，以保证最小经济成本及现役混凝土构件安全工作。

1　裂缝分布的形式

某现役预应力混凝土连续刚构桥全长287.54 m，其设计荷载为公路Ⅰ级荷载，设计安全等级为一级，环境类别为Ⅱ类。对其主梁进行外观检测时发现，在T构部分4#～8#节段范围内，裂缝比较密集，尺寸比较大，具体数据见表1。文中将以4#～8#节段为对象，研究裂缝扩展对现役混凝土结构受力性能的影响。

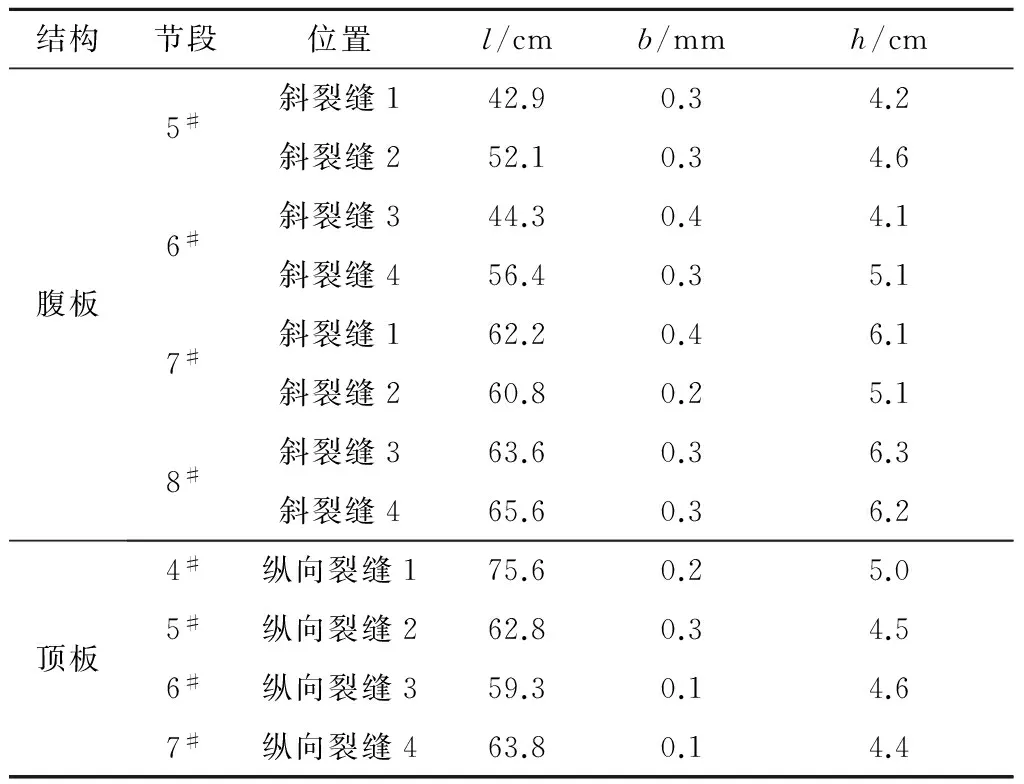
表1　主要裂缝数据

依据相关设计资料，上部主梁采用C55级混凝土，近似认为梁高按直线变化，4#～8#节段的构造(单位：cm)见图1。梁体内部设置横、纵、竖三向预应力钢筋，预应力钢筋的标准抗拉强度为1 720 MPa，其中纵向预应力钢筋采用直径为15.2 mm的低松弛高强钢绞线，张拉控制力设为2 152 kN，横向预应力钢筋也采用直径为15.2 mm钢绞线，张拉控制力设为540 kN；竖向预应力钢筋采用精轧螺纹高强钢筋，张拉控制力为324 kN，普通钢筋采用R235钢筋及HRB335钢筋。由于篇幅限制，未给出节段的钢筋布置图。

a　4#～8#节段纵断面

b　4#节段横断面

c　8#节段横截面

2　计算模型的建立

2.1混凝土参数

利用Solid65 单元来模拟混凝土，采用KINH模型定义混凝土的本构关系，用 Von Mises 强度理论定义混凝土的破坏准则。具体参数见表2，混凝土受压应力-应变曲线见图2。

表2　混凝土材料参数

图2　混凝土受压应力-应变曲线

2.2钢筋计算模型

对预应力钢材采用降温法来施加预应力，温度T为

T=F/AEαl,

(1)

式中：F——预加应力，kN；

αl——线膨胀系数,K-1；

E——钢筋弹性模量,MPa；

A——预应力筋截面面积，mm2。

利用LINK8模拟普通钢筋和预应力筋，采用弹塑性线性强化模型，定义钢筋的本构关系。普通钢筋具体参数见表3，结构钢筋模型见图3。

表3　钢材材料参数

图3　结构钢筋

2.3钢筋混凝土的组合形式

钢筋混凝土的组合可以分成三种形式[10],即整体式模型、分离式模型和组合式模型。整体式模型的缺点是它无法揭示钢筋和混凝土之间的相互作用微机理，它的优点是运算速度快，建模时相对简单方便。采用整体式模型，首先，建立混凝土单元和钢筋单元，然后，对混凝土单元和钢筋单元划分网格，再对两者进行自由度耦合。

2.4裂缝的奇异性处理

裂缝尖端处应力和应变具有r-1/2奇异性，要使有限元的单元形式能够反映这种奇异性，需要解决两个问题：一是构造缝端的奇异单元应具有r-1/2奇异性；二是奇异性单元必须满足与无奇异性区域无常规单元的协调性，以具有足够的精度。为此，计算时需要在空间裂缝周围区域布置一套单元，以满足上述要求[11]，奇异性缝端网格群见图4。

建立带裂缝的有限元模型时，首先,建立如表1中的缝端单元，然后，依次进行奇异性处理，将这些处理过的缝端单元插入到完整桥梁模型的相应位置，最后，将缝端单元同完整桥梁模型进行协调处理，即建立相应的协调方程。文中只给出4#顶板纵向裂缝1的奇异性裂缝有限元模型，见图5。

图4　奇异性缝端网络群

图5　奇异性裂缝有限元模型

2.5荷载及边界条件

该局部结构所受的荷载可分为三类:

(1)直接承受的结构自重和恒载。这部分可以直接加载。

(2)局部结构中的预应力。这部分应力通过前面介绍的降温法来施加。

(3)其他结构部分对局部结构的作用力。

从空间杆系模型的分析结果得到成桥状态时的杆端力，见表4。将其施加到局部结构端截面中心处的节点上，这个杆端力包括其他部分的结构重力作用、所有永久荷载及预应力产生的二次应力、收缩徐变产生的二次力、整体温度作用以及作用在其他部分的活载内力等荷载。钢筋混凝土计算模型见图6。

表4　端部边界条件

图6　计算模型

3　数值计算与结果分析

3.1挠度与应力随裂缝长度的变化

定义表1所有裂缝组成的集合为裂缝群。容易看出，裂缝群中的个体裂缝尺寸杂乱无章，但是现役结构的力学行为是裂缝群综合作用的结果。为讨论裂缝长度对结构受力性能的影响，假定裂缝群个体的宽度、深度为裂缝群对应量的平均值，分析裂缝群个体的长度为裂缝群均值长度的0、1/4、1/2、1、5/4、3/2时结构的受力性能。分析裂缝其他维度尺寸的影响时,同上述分析一致。表5和图7为挠度随裂缝长度的变化数据及趋势。

表5　挠度与应力随裂缝长度的变化

图7　挠度与应力随裂缝长度的变化

从图7可以看到，在模拟荷载作用下，当裂缝长度小于30 cm时，随着裂缝长度的增加，截面的最大挠度几乎没有改变，但是截面开始出现拉应力，而且截面最大拉应力和最大压应力开始缓慢增大，这对应的是正常的带裂缝弹性工作状态。当裂缝长度介于30～60 cm时，随着裂缝长度的增加，截面的最大挠度有所增加，最大压应力和最大拉应力开始急剧增加，并且最大拉应力出现峰值。当裂缝大于60 cm时，随着裂缝长度的增加，截面的挠度急剧增加，最大拉应力开始下降，最大压应力增加到某一峰值时也开始急剧减少。这是因为当裂缝长度增加到某一值时，截面达到其极限承载力，之后开始破坏。拉应力的峰值早于压应力，可以推断当结构出现拉应力破坏时，裂缝首先沿长度方向延伸，然后波及到其他方向，最后彻底破坏。

3.2挠度与应力随裂缝宽度的变化

表6和图8为挠度与应力随裂缝宽度的变化数据及趋势。

表6　挠度与应力随裂缝宽度的变化

图8　挠度与应力随裂缝宽度的变化

从表6和图8可以看到，在特定荷载作用下，当裂缝宽度小于0.05 mm时，随着裂缝宽度的增加，截面的最大挠度、最大拉应力和最大压应力都没有变化。这是因为混凝土本身是带有微观裂纹的材料，当裂缝宽度介于0～0.05 mm内，可以近似看成含微观裂纹的完整混凝土结构在正常工作，所以当裂缝宽度小于0.05 mm时，结构的受力性能不随裂缝宽度变化。当裂缝宽度介于0.05～0.20 mm时，随着裂缝宽度的增加，截面的最大挠度趋于稳定，最大拉应力和最大压应力缓慢增加，此时，结构处于带裂缝正常工作状态。当裂缝宽介于0.20～0.35 mm时，随着裂缝宽度的增加，截面最大挠度明显增加，最大拉应力和最大压应力大幅度上升，并且在某一时刻达到各自的峰值。裂缝宽度大于0.35 mm时，随着裂缝宽度的增加，截面的最大挠度大幅度增大，最大拉应力和最大压应力开始骤减；这是因为截面裂缝开始贯穿，最终导致截面的极限承载能力下降，从而截面破坏。

3.3挠度与应力随裂缝深度的变化

表7和图9为挠度与应力随裂缝深度的变化数据及趋势。由表7和图9可见，当裂缝深度介于0～4.5 cm时，随着裂纹深度的增加，截面的最大挠度趋于稳定，最大拉应力和最大压应力近似呈线性增长。当裂缝深度介于4.5～6.0 cm时，随着裂缝深度的增长，截面最大挠度几乎不变，最大拉应力继续呈线性增长，最大压应力出现峰值。之后，随着裂缝深度的增加，截面的最大挠度急剧下降，最大压应力骤然减小，最大拉应力继续增加，且增加速度明显加快。可以推断，随着裂缝深度的增长，拉应力迅速达到峰值，然后骤然下降；当结构出现压应力破坏时，首先，裂缝沿着深度方向延伸，然后,辐射到其他方向，最后,混凝土结构被压碎。

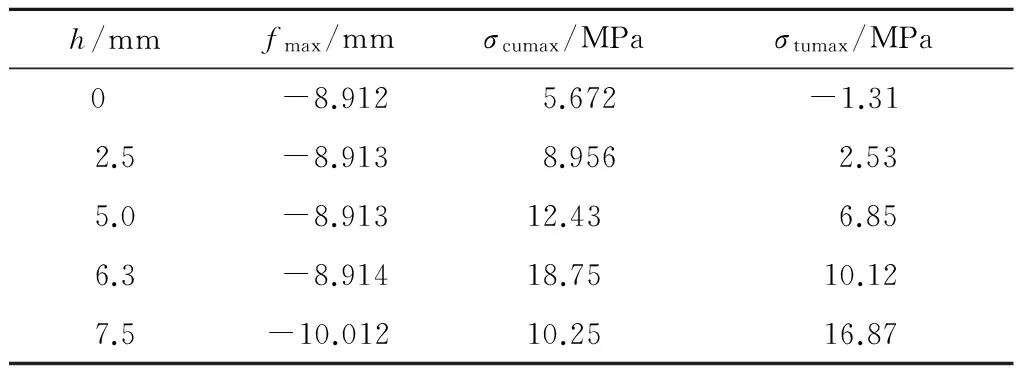
表7　挠度与应力随裂缝深度的变化

图9　挠度与应力随裂缝深度的变化

3.4裂缝修补建议

根据裂纹长度对梁的受力影响，对于宽度和深度尺寸处于裂缝群均值的裂缝而言：当裂缝的长度小于30 cm时，裂缝处于稳定状态；当裂缝的长度介于30～60 cm时，裂缝处于稳定扩展状态；当裂缝的长度大于60 cm时，裂缝处于稳定失稳扩展状态。

由此可以得到裂缝长度(cm)区间：[0，30]，[30，60]，[60，∞)。同理，可得到裂缝的宽度(mm)区间：[0，0.25]，[0.25，0.35]，[0.35，∞)。裂缝的深度(cm)区间：[0，3.5]， [3.5，6]， [6，∞)。分别以[300，250，350]、[600，350，600]作V1、V2，见图10。

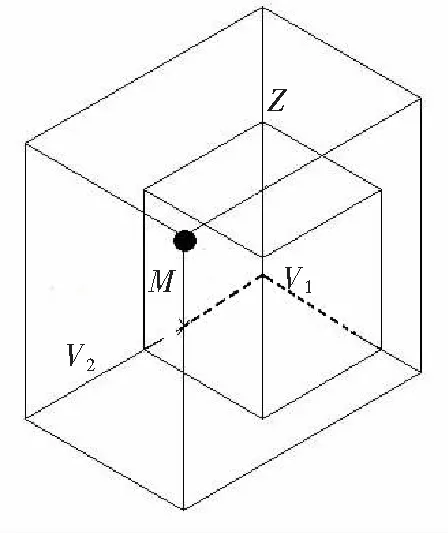
图10　体积模型

将裂缝的长度变换为10-1cm，宽度变换为10-3mm，深度变换为10-2cm，以裂缝尺寸的[长，宽，高]做点，则每个点对于一条裂缝。若点在V1上，则裂缝可以不修补。若点介于V1～V2之间，则裂缝酌情处理。若点在V2之外(包括M)点，裂缝的存在开始减低结构的极限承载力，需要立即修补。

4　结　论

(1)随着裂缝群长度的增加，构件最大拉应力先于最大压应力达到峰值然后开始下降。可以推断，当结构出现拉应力破坏时，裂缝首先沿长度方向延伸，然后波及到其他方向，最后彻底破坏。

(2)当裂缝群宽度小于0.05 mm时，结构的整体受力性能基本不随裂缝宽度的改变而变化，这是因为混凝土本身是带有微观裂纹的材料。

(3)随着裂缝群深度的增加，构件的最大拉应力、最大压应力和挠度都近似呈线性增加，最大压应力达到峰值之后骤减,而最大拉应力继续增加。可以推断，当结构出现压应力破坏时，裂缝首先沿着深度方向延伸，然后辐射到其他方向，最后混凝土结构被压碎。

(4)对于文中工程实际构件而言，V1对应的裂缝不影响结构的极限承载能力；V1之外的部分(包括M点)对应裂缝会使结构的极限承载力降低。

[1]陈红梅. 钢筋混凝土桥梁病害分析及其维修加固[D]. 大连：大连理工大学， 2011.

[2]刘菠. 高速公路桥梁典型病害及建管养对策研究[D]. 重庆： 重庆交通大学， 2012.

[3]JACQUES MATHIVAT. The Cantilever Construction of Prestressed Concrete Bridges [J]. Compute-rs and Structures， 1983， 11(2)： 187-205.

[4]PYOUNG CHEOL CHOI. Serviceability design of prestressed concrete bridges[J]. Journal of Brid-ge Engineering， 1999， 18(1): 1-6.

[5]张立雄.怀柔区公路桥梁混凝土裂缝原因及防治[D]. 北京：北京工业大学， 2012.

[6]陈肇元， 崔京浩， 朱金, 等. 钢筋混凝土裂缝机理与控制措施[J]. 工程力学， 2006(S1)： 86-107.

[7]许莉. 福州市城市桥梁裂缝普查及成因分析[J]. 福建建设科技， 2009(2)： 45-46.

[8]贺拴海， 郭琦， 宋一凡， 等. RC桥梁健康状况及承载能力的动力评估试验[J].长安大学学报： 自然科学版， 2003(6)： 36-39.

[9]李锐. 预应力混凝土连续箱梁桥加固技术探讨[J]. 山西建筑， 2013(2)： 180-181.

[10]ANSYS 11.0结构分析工程应用实例详解[M]. 北京： 机械工业出版社， 2007.

[11]徐世烺. 混凝土断裂试验与断裂韧度测定标准方法[M]. 北京： 机械工业出版社， 2009： 83-84.

(编辑李德根)

Engineering crack propagation effect on mechanical performance of existing reinforced concrete structures

WANGHaijun，GAOShuaiqiang

(School of Civil Engineering， Heilongjiang University of Science & Technology， Harbin 150022， China)

This paper is aimed at eliminating the potential dangers due to active concrete structures working with cracks，some of which have exceeded the limits. The study works towards the singularity treatment of concrete cracks based on the fracture mechanics theory of concrete and using the KINH concrete constitutive model; the application of prestressing force on concrete reinforcing bars using cooling method; and the analysis of the effect of the crack length，width and depth, width direction extension on the mechanical behavior of box beam using the finite element software ANSYS. The results show that the crack group size expansion means increase in both the maximum compressive stress of concrete and the maximum tensile stress; the maximum stress is the most sensitive to the width of the crack. The analysis results provide the proposed model. The study offers the reasonable size range of the crack to be repaired.

concrete structure; crack propagation; tensile stress； compressive stress

2016-02-05

黑龙江省自然科学基金项目(E201460)

王海军(1974-)，男，辽宁省北镇人，副教授，硕士，研究方向：桥梁结构施工与设计，E-mail：hjw741010@sohu.com。

10.3969/j.issn.2095-7262.2016.02.022

U239.9

2095-7262(2016)02-0219-05

A