急倾斜煤层顶煤可放性随机森林模型分类预测及应用

李　伟，　陈海波

(黑龙江科技大学 黑龙江省普通高校采矿工程重点实验室， 哈尔滨 150022)



急倾斜煤层顶煤可放性随机森林模型分类预测及应用

李伟，陈海波

(黑龙江科技大学 黑龙江省普通高校采矿工程重点实验室， 哈尔滨 150022)

为快速、准确地预测急倾斜煤层开采中顶煤可放性等级，借鉴随机森林理论，以 19 个放顶煤工作面为例，选取九大实测指标作为顶煤可放性识别因子，建立急倾斜煤层顶煤可放性识别的随机森林模型。通过五折交叉检验确定模型最优参数，将模型应用到五组急倾斜煤层顶煤可放性评估中。研究表明：随机森林模型预测结果符合工程实际，且当分段数量为 5 时，其精度最优，分别为 91.0%和 100.0%。该研究可以在工程中推广使用。

急倾斜煤层； 可放性预测； 随机森林； 交叉检验

0　引　言

顶煤可放性识别是急倾斜煤层巷道放顶煤开采技术的合理应用及重要依据,顶煤可放性直接决定巷道放顶煤的开采设计与效益[1-3]。为很好地评价顶煤可放性，部分学者在顶煤可放性机制和预测评价等方面进行了大量富有成效的研究工作，尤其是将先进的计算理论和方法引入到顶煤可放性评价中来[1, 4-6]。新的研究成果具有各自的优点，但同时也具有局限性。为此，学者仍在不断探索更为科学有效的评价方法。随机森林 (Random forest, RF)[7]由著名统计学家Breiman提出，是一种基于决策树的组合分类机器学习模型，其内涵是通过对大量分类树的汇总进而提高其模型的预测精度，与支持向量机、神经网络等传统智能算法相比，随机森林预测精度相对较高，且运算量大大降低。随机森林模型在经济学、医学等领域应用，已体现出卓越的性能[8]。在煤炭领域，从急倾斜煤层顶煤可放性的影响因素考虑，利用RF预测，可准确反映输入变量和输出变量的关系，适合于受非线性多元因子影响的顶煤可放性预测。

1　计算原理

1.1RF计算原理

RF 算法利用Bagging( Bootstrap aggregating) 抽样方法从原始数据集中抽取若干个数据，对其使用基尼系数gini为属性度量，建立分类回归决策树。其原理是通过划分决策树各层使初始数据集变得相对纯净，在属性度量上表现为基尼系数下降[9]。随机森林分类器如图 1所示。

图1　随机森林分类器

RF 算法采用多棵决策树并通过投票数对目标归属进行预测，结合相应的预测精度来进行评估，其算法由以下三步实现[10-11]：

(1)从初始样本中抽取ntree个训练子样本，训练子样本大小约占初始样本的2/3。抽取采用bootstrap技术完成，在有放回的抽取中约有1/3的样本未被抽取，这部分样本自然作为对照样本集。

(2)分别对训练样本集建立分类回归树，组建ntree棵决策树的“森林”，从全部M个属性中随机选择mtry(mtry≤M)个最优分段属性进行分支。

(3) 集合决策树预测结果，以投票方式确定新样本的正确归属，分类决策为

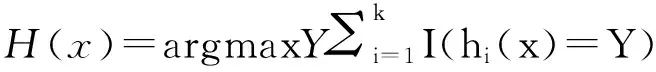
(1)

式中：H(x)——组合分类模型；

hi——单个决策树分类模型；

I(·)——示性函数；

Y——输出变量。

在RF训练过程中，每次抽取将有约1/3的袋外数据未能被抽中，由此产生了袋装误差，袋装误差为无偏估计，趋近于交叉检验误差[12]。

1.2RF模型评价指标

对模型精度评价一般采用混淆矩阵方法，其矩阵为M×M(M为分类数)，用于直观比较分类点和参照点。Kappa统计量表征被评价分类与完全随机分类产生错误减少的比值，其计算公式[13-14]为：

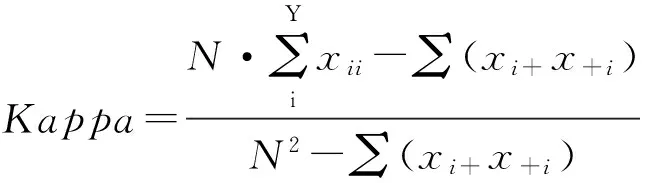
(2)

式中：xi+——第i行和；

x+i——第i列和；

xii——第i行i列主对角线值；

r——混淆矩阵行数；

N——样本总数。

2　RF模型

2.1输入/输出参量的确定

建立急倾斜煤层顶煤可放性的RF预测模型时，需考虑分析资料的易获性和代表性，参考有关文献[1-6]，经综合考虑选取煤层基本顶 (X1)、直接顶 (X2)、底板平整度 (X3)、瓦斯含量 (X4)、采深 (X5)、煤层倾角 (X6)、煤层厚度 (X7)、煤层坚固性系数 (X8)和夹矸程度 (X9) 九个特征参数指标作为随机森林模型评估指标，随后发展起来的距离判别分析模型、Fisher分析模型、SVM模型和神经网络模型等均选用X1、X2、…、X9作为影响顶煤可放性的主要指标，对顶煤可放性类别进行预测，并取得了良好的效果。其中X1和X2用所属分级和类别表示，X1代表煤层基本顶等级为 I ～ IV 级，直接顶X2的等级{1 ～ 4}为{不稳定、较稳定、稳定和坚硬}四类；X3代表平整度，即X3的等级 {1 ～ 4 }分别表示{平整、较平整、不平整、极不平整}；煤层坚固性系数X8用普氏系数 (f) 表示；夹矸程度指标X9=mj/d，其中D代表煤层总厚度，dj代表煤层中总夹矸厚度；其余指标为定量指标用实测值表示。急倾斜煤层顶煤可放性难易程度按四类考虑，即好(A)、较好(B)、一般(C)和差(D)。

2.2仿真数据采集

为验证RF的急倾斜煤层顶煤可放性评价的有效性，选取文献[1, 4-6]中19 个急倾斜煤层放顶煤工作面实测数据为研究对象，其原始数据见表 1。煤层倾角54°～89°，煤层厚度2.0～7.9 m区间，数据集可视化如图2所示。

表1　急倾斜煤层顶煤可放性实测数据及分类结果

图2　各指标数据可视化

2.3参数寻优

RF模型稳定性及泛化能力采用两种方法进行验证。第一，独立测试：利用训练样本集构建的RF模型对测试样本集预测，根据预测结果检验模型；第二， 交叉检验：采用n倍交叉检验策略，即将训练集随机分成n组样本，留出1组作为测试样本，其余n-1组作为训练样本，轮流进行n次，作为测试数据对每组样本进行预测。随机森林五折交叉检验的结果如图3所示，不难发现，当n= 5 时，该模型整体识别精度达到91.0%，Kappa=0.881，为所有分段数目中的最佳。

RF在产生分类结果的同时可计算出变量重要性值，如图4。根据随机森林袋外数据自变量值发生轻微扰动后的分类正确率与扰动前分类正确率的平均减少量计算可知，采深 (X5)和瓦斯含量 (X4)重要度最高，其后依次为煤层倾角 (X6)、煤层坚固性系数 (X8)、煤层厚度 (X7)、夹矸程度 (X9)、煤层基本顶 (X1)、直接顶 (X2) 和底板平整度 (X3)。综上得出：基于树型分类器组合算法的随机森林模型用于顶煤可放性等级预测，具有精度高、训练速度快等优点。

图3　交叉检验参数寻优

图4　RF方法对自变量重要度的排序

Fig. 4Ranking variable importance that associated with classification evaluation by RF method

3　工程实例

为进一步验证急倾斜煤层顶煤可放性RF 模型的有效性，将上述训练好的RF模型应用到资兴矿务局嘉禾煤矿(E1)、资兴矿务局新集煤矿(E2)、开滦矿务局马家沟煤矿(E3)、攀枝花矿务局大宝顶煤矿(E4)和梅田矿务局一矿(E5)等急倾斜煤层顶煤可放性分类预测中，其原始数据如表 2所示。运用上述训练好的RF预测模型对其可放性进行分类识别，各模型评价结果和各矿实际生产情况列入表2中，RF预测结果与实际情况符合。实例E2、E4和E5煤层蕴含低瓦斯，采深相对较小煤层坚固性系数较大，现场观测发现煤体基本不产生变形压力，爆破前放煤巷道变形也很小；而实例E1和E3煤层属高瓦斯煤层，且采深较大，且爆破前放煤巷道已产生较大变形，表明顶煤已经产生变形和破坏，可放性好。现场施工实况验证了顶煤可放性评估的RF模型准确可靠，提高了放顶煤开采效果。

表2　预测样本实测数据与分类结果及实际情况

4　结　论

(1) 选取九大实测指标作为顶煤可放性识别指标，建立急倾斜顶煤冒放性识别的RF模型，用五折交叉验证方法确定模型参数，评价结果与实际情况吻合，准确可靠，提高了顶煤可放性评估水平。

(2) RF在产生分类结果的同时也计算出每个属性变量的重要度，得出煤层采深 (X5)和瓦斯含量 (X4)重要度最高，直接顶 (X2) 和底板平整度 (X3)影响很小，该结论可以为类似工程指标选取提供有益参考。

(3) 评价指标和样本质量决定着评价等级的准确程度，为此，在应用中需更加了解急倾斜煤层顶煤可放性机制并搜集广泛的样本数据库，提高顶煤可放性类别预测模型的可靠性。合理选择识别参量，该模型同样适用于其他煤层可放性识别问题。

[1]王卫军， 朱川曲， 熊仁钦. 急倾斜煤层顶煤可放性识别的神经网络模型[J]. 煤炭学报， 2002， 25(1): 36-39.

[2]陈海波， 李伟， 康健. 结构复杂厚煤层工作面年200万t综放工艺研究[J]. 煤炭学报， 2009， 34(2): 159-162.

[3]王飞. 厚煤层顶煤可放性影响因素分析与评价[J]. 煤炭工程， 2010(4): 40-41.

[4]刘金海， 冯涛， 王卫军， 等. 急倾斜煤层顶煤可放性识别的距离判别方法及应用[J]. 煤炭学报， 2008， 33(6): 601-605.[5]董陇军， 李夕兵， 白云飞. 急倾斜煤层顶煤可放性分类预测的Fisher判别分析模型及应用[J]. 煤炭学报， 2009， 34(1): 58-62.

[6]刘年平， 王宏图， 袁志刚. 急倾斜煤层顶煤可放性识别的支持向量机模型[J]. 煤炭学报， 2010， 35(11): 1859-1862.

[7]BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(2): 25-32.

[8]李宝富， 刘永磊. 冲击地压危险性等级识别的随机森林模型及应用[J]. 科技导报， 2015， 33(1)： 57-61.

[9]张修远， 刘修国. 基于随机森林算法的高维模糊分类研究[J]. 国土资源遥感， 2014， 26(2): 87-91.

[10]李伟贺， 陈志军， 郑建军. 采用核主元成分分析和随机森林的电梯故障诊断[J]. 化工自动化及仪表， 2014， 41(1): 27-30. [11]吴琼， 李运田， 郑献卫. 面向非平衡训练集分类的随机森林算法优化[J]. 工业控制计算机， 2013， 26(7)： 89-90.

[12]黄衍， 查伟雄. 随机森林与支持向量机分类性能比[J].软件， 2012， 33 (6): 1-7.

[13]万建鹏， 官云兰， 叶素倩， 等. 基于综合权重水体指数的水体提取研究—以鄱阳湖为例[J]. 东华理工大学学报： 自然科学版， 2015(2)： 206-211.

[14]努尔比娅乌斯曼， 李新国， 吐尔逊古丽托合提， 等.干旱区典型绿洲土地利用动态变化分析——以且末绿州为例[J]. 新疆师范大学学报： 自然科学版， 2011， 30(3)： 45-48.

(编辑徐岩)

Cavability classification prediction and application of top coal caving for steep seam based on random forest approach

LIWei,CHENHaibo

(Key Laboratory of Heilongjiang University of Science & Technology Mining Engineering College of Heilongjiang Province, Harbin 150022,China)

This paper is motivated by the need for the rapid and accurate prediction of the cavability classification of top coal in steep seam. The study produces a novel method based on the random forest model for top coal cavability identification using 9 indexes as the discriminating factors for top coal cavability, applying the 19 groups of caving working face as a verification example, and using the theory of random forests. The study includes determining the optimal parameters of the RF model using 5-fold cross-validation and evaluating top coal cavability by applying 5 groups steep coal seam . The research reveals that Random forests model could give prediction results conforming to engineering practice and thus features the optimal accuracy of 91.0% and 100.0% respectively when the segment is 5. The results may promise a wider use in engineering.

steep seam; cavability prediction; random forest; cross-validation

2016-05-06

黑龙江省普通高等学校采矿工程重点实验室开放课题(2014KF04)

李伟(1979-)，男，满族，辽宁省锦州人，副教授，硕士，研究方向：采矿工程、矿井信息化，E-mail：lw7709@126.com。

10.3969/j.issn.2095-7262.2016.04.005

TD821

2095-7262(2016)04-0373-05

A