基于Bézier提取NURBS的二维线弹性等几何分析

程正南，黄璐璐，王闪

（安徽工业大学机械学院，马鞍山　243002）

基于Bézier提取NURBS的二维线弹性等几何分析

程正南，黄璐璐，王闪

（安徽工业大学机械学院，马鞍山243002）

等几何分析方法是用统一的语言描述几何模型和计算模型，打通了CAD与CAE模型上的不一致问题。研究基于Bézier提取NURBS的二维线弹性等几何分析方法，将Bézier提取操作符应用于NURBS，使NURBS的基函数分解成Bernstein多项式，形成基于Berntein多项式的NURBS形式。相对于传统有限元分析，此方法Bézier单元高阶连续，求解精度更高；并以薄壁圆形梁模型算例验证了该等几何分析的实用性。

等几何分析；非均匀有理B样条；Berntein多项式；有限元分析

传统工程实践中，计算机辅助设计（CAD）与计算机辅助工程（CAE）是基于两个不同的平台，两者之间的信息是单向传输，即在CAD系统中进行建模，通过CAD与CAE的接口导入到CAE分析系统内，CAE软件计算之前通过有限元软件把CAD模型进行前处理，也即网格划分，这样无法与CAD几何建立起直接的联系，这样的单向信息传输使得在计算分析过程复杂耗时。

Hughes等［1］从统一CAD与CAE的角度，提出了一种新的以样条理论为基础的数值计算方法-等几何分析［2］（Isogeometry Analysis，IGA）。其思想是将样条函数构建精确几何模型［3］，用此样条基函数作为形函数分析该几何模型，使得设计、分析模型采用统一的描述，解决了传统数值方法的求解域与几何模型非一致问题，不仅提高了求解精度也节约了大量的时间。等几何分析优势多，应用广，广泛应用于板壳分析［4］、流体力学［5］、电磁场［6］等。虽然等几何分析方法应用和优势众多，但对于特殊结构体中，存在局部不能进行细化等问题，为此，Bazilevs［7］等人及王平［8］等人将T样条以及PHT样条相继用于等几何分析方法以弥补NURBS的不足。Bézier、B样条与NURBS的意义众多［9］，利用Bézier与NURBS优势互补的性质在等几何分析应用中较少。

本文研究了基于Bézier提取NURBS等几何分析方法，通过节点嵌入的方式把Bernstein多项式引入到NURBS基函数中，形成新的基于Bernstein多项式的NURBS形式。并将该方法应用到经典的二维线弹性实例中。最后将其计算结果与经典有限元软件计算的结果进行了比较。

1　等几何分析基础

1.1B样条基本概念

节点矢量Ξ=｛ξ1，ξ2，…ξi，ξi+1，…ξn+pmax+1｝是一个非减的实数序列。其中，ξi称为节点，Ξ称为节点矢量，p为阶次，n为最高阶的基函数个数。在等几何分析中，参数空间中的单元是由节点划分的。用Ni，p（ξ）表示第i个p次B样条基函数，其定义为：

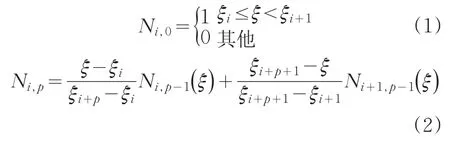
B样条曲线定义为：

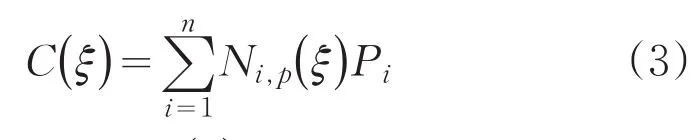
｛Pi｝是控制点，Ni，p（ξ）是定义在节点矢量上的p次B样条基函数。

B样条基函数的基本性质：非负性、单位分解性、紧支性、高阶连续性、递归求导性、线性无关性和非插值性等［9］。

1.2NURBS基本概念

NURBS理论包含了所有B样条理论的性质，同时它本身也有自己的优点。NURBS在B样条方法的基础上引入了权因子与分母，使得在设计CAD模型时更加灵活方便。当权重均为1时，此时的NURBS也即B样条。

NURBS曲线，如图1（a）所示，在ξ方向上p次的NURBS曲线定义为：

NURBS曲面，如图1（b）所示，一张在ξ方向p次、η方向q次的双变量分段有理矢值函数的NURBS曲面为：

图1　几何图形（黑色为控制点）

2　等几何分析基本原理

2.1Bézier曲线［9］

一条p次Bézier曲线定义为

式中，Bernstein多项式为

其中p为阶次，｛Pi｝为控制点，令B1，0（ξ）=1；如果i＜1或i〉p+1，则B1，0（ξ）=0。

2.2Bézier提取运算符与应用

2.2.1NURBS中节点嵌入

将待插入的节点ξ*∈［ξk，）ξk+1插入节点矢量Ξ形成新的节点矢量为Ξ=｛ξ1，ξ2，…，ξk，ξ*，ξk+1，…ξn+p+1｝，节点向量被更新后，以前与节点矢量Ξ相匹配的控制点和权重也需更新，得到控制点权重及其坐标更新公式分别为：

2.2.2Bézier提取运算符

在B样条原有的节点矢量中加入其内部已有的节点，并且其重复度等于曲线的次数时，则B样条曲线与Bézier曲线形状一样，只不过相应的控制点会增加，此时曲线连续性和单元之间连续性并未改变［10］。

Bézier分解是一个节点嵌入的操作，Bézier提取运算符C是根据当初始节点矢量嵌入新的节点矢量后，控制点做出相应的变化规则。相当于细化规

节点嵌入后的控制点变化

根据B样条曲线公式（2），嵌入节点后的Bézier

曲线和原始B样条曲线几何参数和形状未改变，得

由上式得B样条基函数与Bernstein多项式的关系为

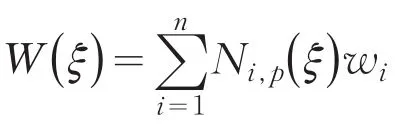
其中，wb=CTw（w为NURBS权重点）因此NURBS的基函数公式变为

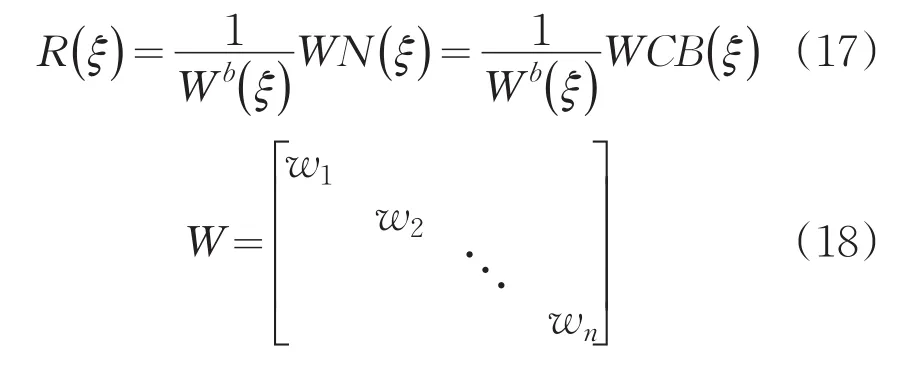
得出Bézier控制点与NURBS控制点的关系为：

则NURBS曲线用Bernstein多项式表示为

根据单变量提取运算符，同样二变量提取运算符可应用于NURBS曲面中。二变量提取运算符可以被定义为单变量提取运算符的张量积形式

2.3线弹性

根据虚功方程［11］，二维线弹性等效积分弱形式为：

应力与应变的关系为

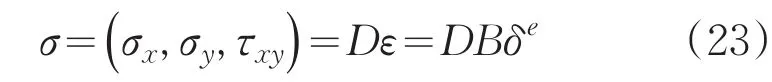
式中，Ri是NURBS基函数，aei是控制点P的位移，N为控制点总数。将式（25）、（26）带入式（24），由于虚位移是任意的，经过化简得

3　实例分析

以四分之一薄板圆形梁为例，内外半径分别为a和b。定义参数，弹性模量E=1MPa，泊松比μ= 0.25，a=5mm，b=10mm。

图2　四分之一薄壁圆形梁

3.1右侧底部1/4处受到竖直向下的集中力，大小为1N

边界条件及受力如图2（a）所示。假设曲面x方向与y方向节点矢量均为［0 0 0 1 1 1］。将圆形梁划分为4x4单元数，取2阶NURBS和Bézier单元进行粗略的网格细分如图3所示。

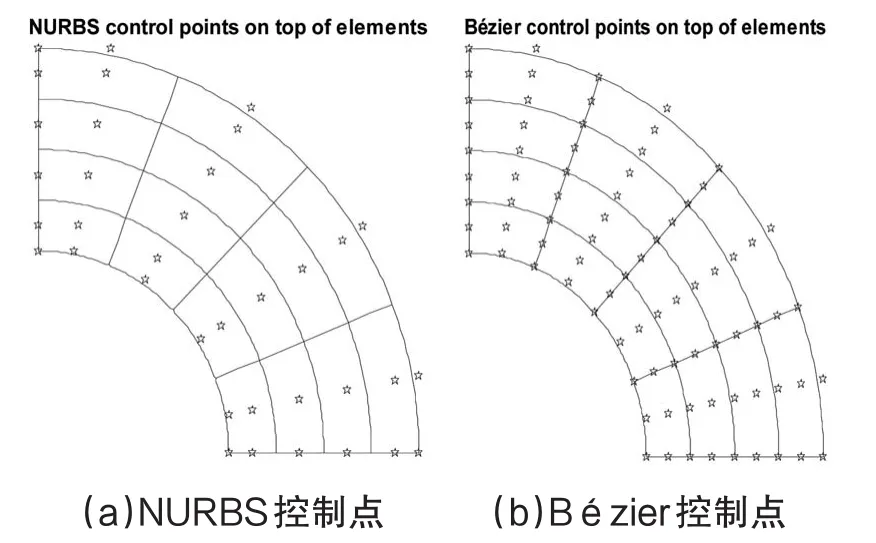
图3　模型离散4x4单元（黑色五角星为控制点）

从图3可看出Bézier控制点多于NURBS控制点。由于分析均是计算单元上控制点受力情况，因此这将对计算精度有重要影响。

图4　有限元分析和等几何分析的第一主应力（单位：MPa）

传统有限元分析与等几何分析Mises应力云图如图4所示。从图4可看出，等几何分析结果与经典有限元分析的结果很相近，Mises应力最大值均发生在最左上角处，其值为2.6MPa附近。

3.2底部受到竖直向上的均布线拉力，大小为0.2N/mm

受力及边界条件如图2（b）所示。当模型的网格不断细化，也即模型的单元数不断增加时，有限元结点和等几何分析控制点不断增多，A点的位移计算也会趋于稳定，其结果如表1所示。传统有限元与等几何计算方法的数值解随单元数增加的变化趋势如图5所示。

图5　有限元分析与等几何分析计算结果比较

表1　等几何分析与有限元分析A点纵向位移（单位：mm）

由图5可知，在单元数相等的情况下，等几何分析远比有限单元分析的精度高的多。从等几何分析看出，阶数等于3，初始划分结果接近真实值，这在复杂的几何体表现的更为明显。并且圆梁模型在等几何离散过程中始终保持着原有形状，而有限元离散中模型简化为多边形。

4　结语

通过节点嵌入方法，引入Bézier提取NURBS等几何分析方法，用此方法对经典的1/4圆形梁进行分析。从上面可知，该方法对单元细分方面更方便，由NURBS基本性质，此方法单元高阶连续。最后把等几何分析在求解的精确度方面与有限分析做了比较，结果表明等几何分析的求解精度明显优于有限元分析，且计算效率和单元的间的连续性方面也优于有限元分析。在未来工作中等几何分析方法的优势将会更突出。

［1］Hughes T J R，Cottrell J A，Bazilevs Y.Isogeometric analysis：CAD，finite elements，NURBS，exact geometry and mesh refinement［J］.Computer Methods inAppliedMechanicsandEngineering，2005，194（39-41）：4135-4195.

［2］Cottrell J A，Hughes T J R，Bazilevs Y.Isogeometric analysis toward integration of CAD and FEA［M］.New York：John Wiley&Sons，Ltd，2009.

［3］Xu G，Mourrain B，Duvigneau R.Analysis-suitable volume parameterization of multi-block computational domain in isogeometric applications［J］.Computer-AidedDesign，2013，45（2）：395-404.

［4］Benson D J，Bazilevs Y，HSU M C，et al.Isogeometricshellanalysis：theReissner-Mindlinshell［J］.Computer Methods in Applied Mechanics and Engineering，2010，199（5-8）：276-289.

［5］Ming-ChenHSU，AkkermanI，BAZILEVSY. High-performance computing of wind turbine aerodynamics using isogeometric analysis［J］.Comput& Fluids，2011，49（1）：93-100.

［6］Buffa A，Sangalli G，Vazquez R.Isogeometric analysis in electromagnetics：B-splines approximation［J］. Computer Methods in Applied Mechanics and Engineering，2010，199（17-20）：1143-1152.

［7］Bazilevs Y，Calo V M，Cottrell J A，et al.Isogeometric analysis using T-splines［J］.Computer Methods in Applied Mechanics and Engineering，2010，199（5-8）：229-263.

［8］Wang Ping，Xu Jinlan，Deng Jiansong，et al.Adaptive isogeometric analysis using rational PHT-splines［J］.Computer-Aided Design，2011，43（11）：1438-1448.

［9］Piegl L，Tiller W.The NURBS book［M］.2nd ed. New York：Springer，1997：81-116.

［10］Borden，M.J.，M.A.Scott，J.A.Evans，and T.J. R.Hughes.Isogeometric finite element data structures based on Bézier extraction of NURBS［J］.International Journal for Numerical Methods in Engineering，2011，87：15-47.

［11］徐芝纶.弹性力学［M］.第三版.北京：2002.8：105-128.

Isogeometric Analysis of Dimensional Linear Elasticity Based on Bézier Extraction of NURBS

CHENG Zhengnan，HUANG Lulu，WANG Shan
（School of Mechanical Engineering，Anhui University of Technology，Maanshan，243002）

In isogeometric analysis（IGA），identical language is shared for geometric design and numerical simulation，which solves the inconsistencies between CAD and CAE model.IGA of dimensional linear elasticity is based on Bézier extraction of NURBS in the article，the Bézier extraction operator is used in description of NURBS，then the Bézier extraction operator decomposes the NURBS basis functions to Bernstein polynomials，which forms new NURBS based on Bernstein polynomials.With respect to the traditional finite element analysis（FEA），which generates high degree-continuous of Bézier elements，at the same time the solving accuracy is higher；The thin-walled circular beam model is chosen as an illustrative example to verify the practicability of IGA.

isogeometric analysis；NURBS，Bernstein polynomials；finite element analysis

TP122

A

1672-9870（2016）04-0130-05

2016-03-17

教育部人文社科研究项目（13YJAZH106）

程正南（1989-），男，硕士研究生，E-mail：604834726@qq.com