基于插值和曲面拟合的图像亚像素配准算法

赵洋，杨丹蕾，刘博宇，杨进华

（1.长春理工大学光电工程学院，长春　130022；2.吉林大学通信工程学院，长春　130000）

基于插值和曲面拟合的图像亚像素配准算法

赵洋1，杨丹蕾2，刘博宇1，杨进华1

（1.长春理工大学光电工程学院，长春130022；2.吉林大学通信工程学院，长春130000）

图像配准在很多领域有着广泛的应用，如在计算机视觉、识别模式、军事、医学成像方面等方面，而且像素级的配准精度远远不能满足要求，需要达到亚像素级的图像配准。本文在传统三次曲面拟合的基础上，提出了一种改进的亚像素精度配准算法，该算法首先找到像素级配准位置（u1，v1），之后在附近区域进行灰度插值，在图像插值过程中采用的是具有在节点处具有二阶连续导数的三次样条插值和双立方插值法。最后经过曲面拟合求得亚像素配准结果。实验结果表明，与传统的曲面拟合算法相比，本文提出的算法在精度上得到了明显的改善，精度可以达到0.01pixel。

图像配准；亚像素；样条插值；双立方插法

图像配准作为计算机是觉得关键技术之一，是在不同时间、不同地点、不同相机拍摄的两幅图片像中找到一组人们感兴趣的同名点的过程，而对于超分辨率遥感图像生成、高精度3D重建、视觉定位、医学图像等应用中的关键问题，配准结果需要达到亚像素级级别。

按匹配过程可分为基于图像特征的图像配准和基于灰度的图像配准。［1］他们的主要区别在于是否包含分割步骤。基于特征的方法包含图像的分割过程，用于提取图像的特征信息，然后对图像的显著特征进行配准。常用的图像特征点包括点特征、直线特征、边缘以及统计矩等。［2］特征点提取算法可分为特征点提取算子（Harris算子、SUSAN算子）、线特征提取算子（LoG算子、Canny算子）。基于特征的方法往往具有操作简单，配准速度快，可对图像完成像素级的边缘定位，但同时需要人工干预，特征点获取比较困难等缺点，给配准结果带来不确定性。而且当CCD和光学镜头的分辨率受到局限，这时改变软件比改变硬件更加有效，所以，将图像配准达到亚像素级别将是行之有效的方法。

基于灰度的配准方法无需进行图像的分割与特征的提取，直接用图像的统计信息作为配准的相似性度量。利用两幅图像的灰度信息度量之间的相似性。基于灰度的配准方法，只对灰度进行处理，可避免主观因素的影响。

从20世纪70年代就有很多人在亚像素图像配准方面做了大量研究，现有的亚像素配准方法基本可以归结为3类，［3］基于插值拟合的方法，扩展相位相关法和解最优化问题发法。解最优化问题运算量一般较大，相位相关法性能一般较差，而基于插值拟合的方法运行速度慢，难以得到应用。目前，亚像素图像配准技术大多集中于曲面拟合和梯度法，而针对运用标准互相关匹配的方法则比较少，主要原因是相关匹配运算量大，相关函数进行搜索时只能以像素为单位进行移动。但随着计算机硬件处理速度的不断提高，相关匹配的速度慢，运算量大的困难逐渐的被克服，本文提出了一种基于灰度图像插值的配准算法，在以往的曲面拟合算法中，他们都是由配准模板与其同等大小的子区窗口计算相关系数的来的，因此在拟合曲面时，局限在整数像素精度上，而模板实际的配准点不一定在整数像素位置上，导致配准不准确。据此，在找到像素级配准点（u1，v1）之后，对图像进行灰度插值，然后把相关系数最高点作为拟合窗口中心，使其更接近真实值，并且，拟合节点也由原来的整数像素变为0.2个像素长度，最后，拟合曲面的峰值点就为亚像素配准点。

1　灰度图像的像素级粗配准

1.1灰度互相关算法原理

本文采用定位精度较高的基于灰度标准互相关匹配算法，首先根据图像特征的大小在其中一幅图像上选取模板，此算法是将模板在另一幅图像上遍历搜索，依次计算互相关度，互相关值最大的一点就为最佳匹配点，定位精度达到了像素级，标准归一化互相关公式如下：

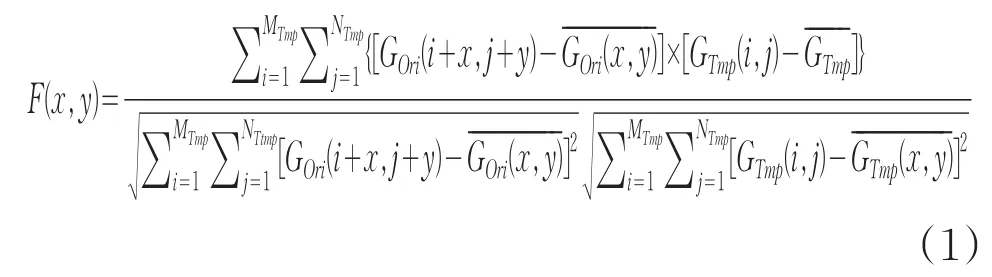
1.2快速像素级粗匹配过程［4］

在互相关算法中，实验所拍摄的图像尺寸为（1280×960）pixel，模板的小为（160×160）pixel，由于每个像素的灰度值都参与计算，所以计算量非常大，为了减少匹配过程的计算量，本文在搜索策略上做出了改进，有效的解决了运算速度慢的问题。

首先，对模板图像和待搜索图像进行4倍的双线性降采样，降采样后的模板尺寸变为（40×40）pixel，待配准图像大小为（320×320）pixel，如下图所示。这时，通过标准互相关算法可以找到降采样后的相关峰值坐标（u0，v0）。通过4倍降采样后的相关峰值坐标估算原始待配准图像的坐标，大约在（4u0，4v0）附近。

图1　模板和待配准图像进过4倍的降采样

2　灰度图像插值函数的基本原理

目前，已经有很多种插值算法，例如最邻近法、双线性插值法等，由于插值方法对后面的曲面拟合会产生影响，为了更好的达到插值效果，本文采用了精度较高的三次样条插值和双立方插值法。

2.1双立方插值［5］

在图像插值过程中，不仅要考虑直接邻近点对它的影响，还应该考虑该点周围16个邻点的灰度值对它的影响。采用sinc函数进行灰度插值，可以准确的得到采样点间任意点的值，插值函数s（x）=sin（πx）（πx）的特性图如下：

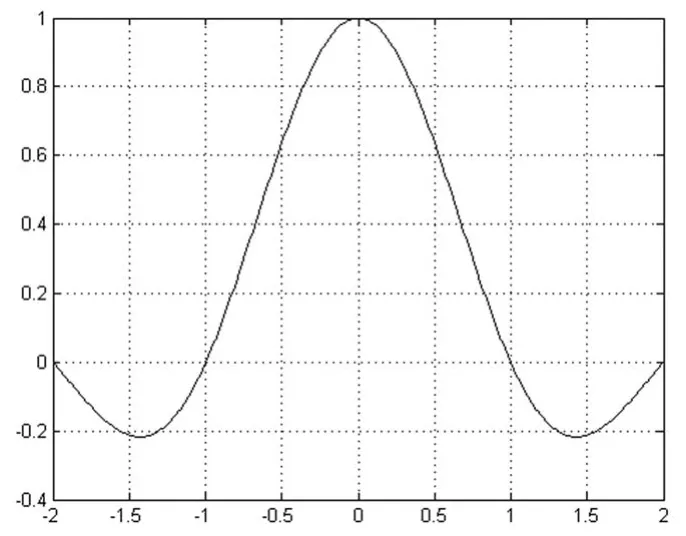
图2　sinc函数曲线图

骤插值算出f（x0，y0）：

2.2三次样条插值［6］

三次样条插值的本质是三次多项式插值，并且在节点处有连续二阶导数，所以，插值结果比较精确。在区间［a，b］进行划分：a=x0＜x1＜…＜xn=b，设函数y=f（x）在节点x上的值为yi=f（xi）（i=0，1，…，n）。

在函数S（x）于［a，b］有二阶连续导数，在每个小区间［xi，xi+1］上是三次多项式，则S（x）是节点x0，x1，…，xn，上的三次样条函数，如果在节点上还满足

则称是三次样条插值函数。

x y x0 y0 x1 y1……xn yn

求一个三次多项式满足条件

（1）S（xi）=yi；（i=0，1，…，n）

（2）有二阶连续导数，特别在节点上应满足连续性条件，即对i=0，1，…，n-1成立

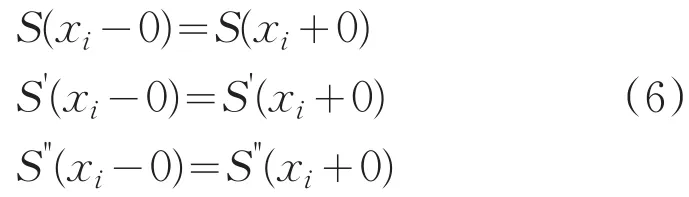
三次样条插值函数具有比其他插值函数更好的稳定性，保证曲线的光滑性，在三次样条插值中，插值节点处的函数值的波动只对这个节点两边的分段有影响，而对里该点较远的分段影响会逐渐减小，因此，样条插值法具有较好的稳定性。本文采用的是样条插值的第三类边界条件，即第一个节点和最后的一个节点的一、二阶导数相等。

3　改进的配准算法

在以往的二元三次拟合算法中，所采用的相关系数都是由整数像素子区域中的点计算得来的，但是，模板真实的最佳配准点可能不在整数像素位置处。这时，如果按照整数像素节点的互相关值来计算，得到的结果将是不准确的，对精度的影响很大。综上，本文提出了一种改进的曲面拟合算法，首先，由快速像素级粗匹配过程，找到互相关值最大的点，之后利用插值的方法对原图进行重新采样，在灰度插值过程中，对每个像素进行五细分，五细分的主要有两个原因，一是如果细分份数越高，后面的互相关式计算上付出的时间代价会更高，而是如果细分份数少的话，拟合节点距离也同样变大，会影响拟合曲面的精度。五细分使图像达到亚像素级别，在对细分之后的模板和待配准图像重新进行互相关运算，以0.2pixel为拟合节点距离。

二元三次拟合曲面表示为：

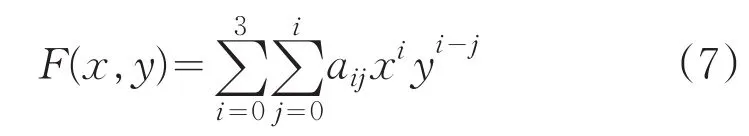
在以图像五细分的亚像素级最佳配准点（u1，v1）为中心，（21×21）pixel区域内，求取上式中的10个待定系数，利用最小二乘法可求得，最终解方程组得到F（x，y）的极大值坐标，即为亚像素配准点。

具体的改进算法步骤如下：

（1）利用降采样的方法快速的找到像素级配准位置（u1，v1）。

（2）在求得（u1，v1）之后，为了减少运算时间，在待配准图像上截取以（u1-20，v1-20）、（u1-20，v1+40+ NTmp）、（u1+40+MTmp，v1-20）、（u1+40+MTmp，v1+40+ NTmp）、为顶点的子区域，对原模板和上图分别进行灰度插值。并且计算互相关值，重采样之后的最佳配准点坐标为（u2，v2）。

（3）以点（u2，v2）为中心，选取21×21个临近测试点，再进行二元三次曲面拟合，最后曲面的峰值坐标即为亚像素配准结果。

4　测量实验与结果

为了验证基于插值的改进的配准算法的性能，准确的评价该算法的精准度，本文利用Matlab软件进行编写程序。利用Matlab软件中提供的peaks（峰值）函数在区间［-3，3］和［-3，3］内的函数分布情况模拟实际CCD中的光强分布。由于相机在成像过程中，光线经过镜头透射在CCD像上，而相机生成的图像灰度值的大小则是分布在单个像元的光强的平均值，所以，利用连续函数曲面模拟CCD的光强分布时，应该计算某一区域内的平均值，来代替相应点的灰度值，本文在模拟过程中，首先以0.05×0.05个单位长度来模拟单个CCD像元，也就相当于成像CCD是由121×121个像素构成的，得到图像Px。之后再以0.01×0.01的区域计算曲面的平均值，来模拟把121×121个像素的图像进行5细分，得到一个605×605个像素的图像Qx，并且最为后续工作中的待配准图像。最后利用三次样条插值和双立方插值的插值方法，对Px进行五倍的放大，并且在放大后的图像上截取模板Pt与Qx进行互相关运算。

图5为利用三次样条插值对图4进行五倍的细分，变成605×605个像素大小的图像，图6为利用双立方插值对图4进行5倍的细分，同样得到606×605个像素大小的图像。

在图像Px截取模板Pt过程中，始终保持模板的大小不变，为了更好地验证该插值方法的性能，每次以0.01个单位长度（0.2个像素）作为目标，移动模板窗口，依次与Qx进行互相关运算，最终进行三次曲面拟合运算。

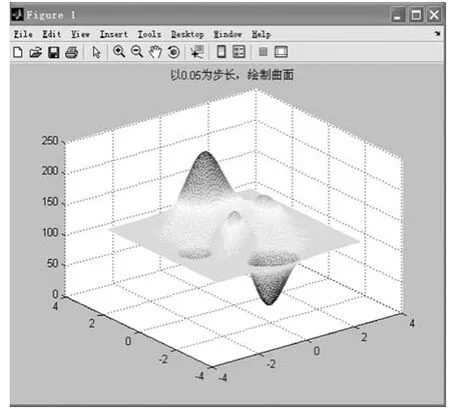
图3　Peaks函数三维曲面图

图4　121×121的图像Px

图5　

图6　

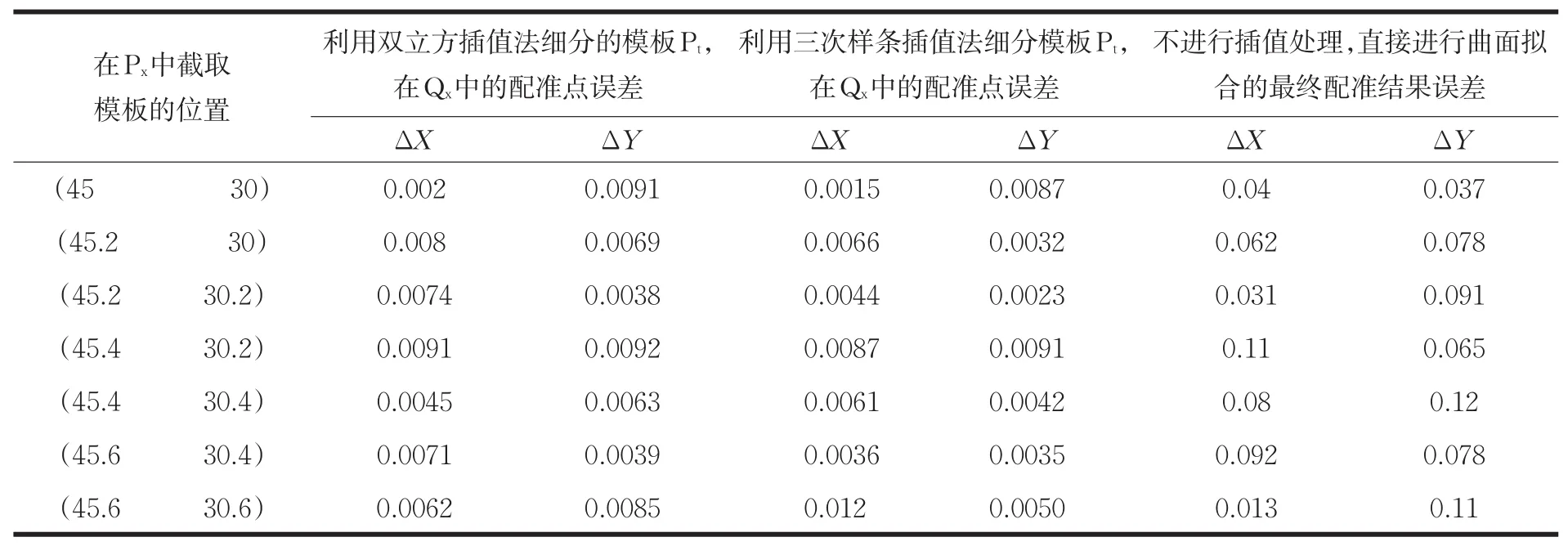
表1　不同插值方法的结果误差（单位：像素）

本文分别做了三组不同的实验：1）对模板通过三次内插法进行插值处理，2）对模板进行三次样条插值算法进行细分处理，3）不对模板进行任何处理，直接进行曲面拟合。最终的配准结果误差如表1。

在以上的实验中，利用双立方插值的误差均值为0.009299个像素，而利用三次样条插值法的误差均值为0.008个像素，不通过插值法处理，直接进行三次曲面拟合的误差均值为0.0909个像素。

经过实验的验证可以看出，采用不通过插值处理的传统配准算法进行配准时，尽管插值时间短，对计算机没有过高的要求，但是配准精度远远达不到本文提出的基于插值的改进的亚像素精度配准算法，与传统的算法相比，配准精度优越于传统三次拟合算法，不足的是计算消耗时间稍高于传统的三次拟合算法。

5　结论

本文在传统曲面拟合算法的基础上提出了改进，针对以往将整数像素为拟合节点进行二元三次拟合，采取了双立方插值和三次样条插值，拟合节点变为亚像素级，并且，得到更加精准的互相关系数，最终经过三次曲面拟合，计算亚像素配准坐标，通过实验验证了该算法精度高于0.01个像素，与传统的曲面拟合算法相比有明显的优势。

［1］王鲲鹏，徐一丹，于起峰.红外与可见光图像配准方法分类及现状［J］.红外技术，2009，31（5）：270-274.

［2］杨杨，张田文.焦点检测算法评价方法的研究［J］.哈尔滨工业大学学报，1998，30（2）7-10.

［3］黎俊，彭启敏，范植华.亚像素级图像配准算法研究［J］.中国图像图形学报，2008，13（11）：2070-2075.

［4］申琳.高精度双目测距研究［D］.长春：长春理工大学，2011.

［5］张德丰.数字图像处理［M］.1版，北京：机械工业出版社，2009.

［6］李庆扬，王能超，易大义.数值分析［M］.5版.北京：清华大学出版社，2008：22-46.

An Sub-pixel Precision Registration Algorithm Based on Image Interpolation and Fitting

ZHAO Yang1，YANG Danlei2，LIU Boyu1，YANG Jinhua1
（1.School of Optoelectronic Engineering，Changchun University of Science and Technology，Changchun 130022
2.Jilin University College of Communication Engineering，Changchun 130000）

Image registration is applied extensively in many fields，such as in computer vision，recognize patterns，military，medical imaging，and so on.registration at pixel level can’t meet our requirements.registration Should be at Sub-pixel level.An improved sub-pixel registration algorithm is proposed based on cubic surface fitting method.First，find the pixel registration coordinates（u1，v1）.Second，there is an image interpolation process.We use cubic spline interpolation and bicubic interpolation in the image interpolation process，and cubic spline interpolation has the second-order continual derivative in the node.Finally，we get the sub-pixel registration results rely on cubic surface fitting method.The experiment results show that the algorithm relatively to the general cubic surface fitting has a slight increase in calculation error.The experim ental results show that the algorithm maintains a high precision of sub-pixel extraction.

Image registration；Sub-pixel；spline interpolation；cubic

TP391

A

1672-9870（2016）04-0109-04

2016-03-20

赵洋（1991-），男，硕士研究生，E-mail：983018918@qq.com

杨进华（1969-），男，教授，E-mail：yangjh@cust.edu.cn