一种改进的摄像机线性标定优化方法

刘博宇，赵洋，杨进华

（长春理工大学光电工程学院，长春　130022）

一种改进的摄像机线性标定优化方法

刘博宇，赵洋，杨进华

（长春理工大学光电工程学院，长春130022）

现有的摄像机标定方法没有将高精度和简便性很好的衔接在一起。提出一种新的标定优化方法。首先选择主点位置在图像中心，纵横比为1作为初始条件；接着利用改进的摄像机线性标定方法，得到在同一摄像机坐标系下不同图像上所有标定点的摄像机坐标；最后利用摄像机坐标系下的这些三维点来优化内、外参数。实验结果表明：本文提出的标定方法得到的焦距误差在0.1mm以内，主点位置的最大误差在2pixel左右，测试点的最大误差控制在0.5pixel以内。本文提出的标定方法是一种简单、高精度的标定方法。

摄像机标定；摄像机模型；线性标定

在计算机视觉、工业测量、智能机器人导航以及质量控制等领域中，通过摄像机的标定，可以确定摄像机的内外参数，从而实现将二维平面信息转换成三维立体信息。摄像机标定就是物体通过摄像机的成像模型投影到像平面上，物体上的点与其成像点一一对应，并由其成像模型的参数决定，确定这些摄像机成像模型参数的过程被称作摄像机标定。摄像机的内参数主要包括主点坐标焦距f还有纵横比等，摄像机的外参数是指摄像机坐标系相对于世界坐标系的位姿关系，包括旋转矩阵R和位移向量t。摄像机的标定精度和算法的稳定性直接影响其结果的可信度，因此摄像机标定是一项十分重要的工作［1］。

目前，常用的摄像机标定方法包括直接线性法［2］、非线性优化法［3］、Tsai两步法［4］和张正友的平面标定法［5］等。其中直接线性法忽略了镜头畸变带来的影响，标定精度比较低；非线性优化法标定耗时较长，算法繁琐，对初始值依赖较大，如果初始值选择的不合适标定结果误差也随之较大；Tsai的两步法是先线性求解出部分参数，再引入非线性优化求解其余的摄像机参数，其标定过程虽然简单，但它假定主点位置在图像的帧存中心，纵横比为1，并未对几个重要的内参数进行标定，这将严重影响标定精度；张正友的平面标定法是利用摄像机拍摄平面标定板的不同角度姿态的图像，通过多幅二维图像信息的分析处理来获取摄像机参数，其方法先用线性法求解部分参数，再考虑镜头畸变利用最大似然原则对参数进行非线性优化，通过获取内参数以及单应性矩阵求解出摄像机的外参数，最终完成摄像机内外参数的标定，但在标定的过程中需要不断的调整标定板的位姿和角度，过程相对繁琐复杂，且标定板的角度和标定板上标定点的数量都会严重影响标定的精度。这几种常用的摄像机标定方法都没有兼容简便性和高精度性，针对这一点，本文提出了一种新型的线性标定优化方法。

1　摄像机模型

摄像机针孔透视模型是普遍应用的摄像机成像模型，它反映了目标物体上各点的世界坐标经过摄像机投影到图像平面上与其对应点的理想图像坐标的转换关系。但镜头中光学元件在加工和装调的过程中都会存在一定误差，这就造成了摄像机像平面上的理想成像点与实际成像点之间存在一定的偏差。摄像机镜头的主要光学畸变包括径向畸变、偏心畸变和薄透镜畸变［7］。在选择畸变模型时，并不是畸变参数选择越多对畸变改正越有利；相反畸变参数选择过多反而会降低精度。因此通常仅需考虑径向畸变所带来的误差。

图1　一阶径向畸变针孔模型

如图1所示，该模型共有4个坐标系，分别是世界坐标系OwXwYwZw、摄像机坐标系Ocxcyczc、图像平面坐标系oxy和计算机图像坐标系Ouv。空间中任意点Q在该摄像机模型下，从世界坐标系到计算机图像坐标系的变换分为4步［8］：

（1）Q点的世界坐标与其在摄像机坐标系下坐标的转换：

世界坐标系OwXwYwZw通过旋转矩阵R和平移向量t与摄像机坐标系重合。

（2）Q点在摄像机坐标系下的坐标与其理想成像点在图像平面坐标系下的坐标转换：

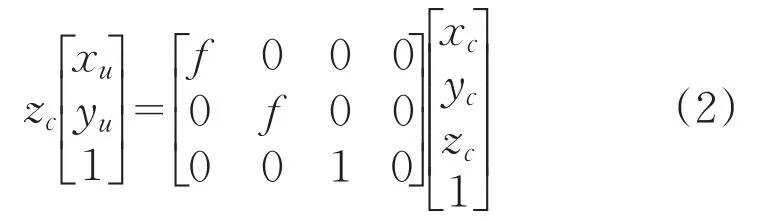
（3）实际成像点在图像坐标系下的坐标为：

（4）Q点实际成像点的图像坐标与其计算机图像坐标的转换：

2　基于重心法提取标定点的图像坐标

本文采用MVTec公司的7×7的halcon标定板进行标定，其尺寸为0.3m×0.3m，边框内圆点的中心距为0.0375m，精度为0.001mm，如图2所示。

图2　HALCON标定板

用重心法提取标定板上椭圆的重心时，当标定板与摄像机像平面不平行时，在CCD图像上提取的椭圆重心与标定板上椭圆重心并非是同一个点。

如图2所示，标定板侧面与CCD平面成α夹角，其中CD代表其中一个标定圆的直径，O是它的重心位置，O1为摄像机原点，则：

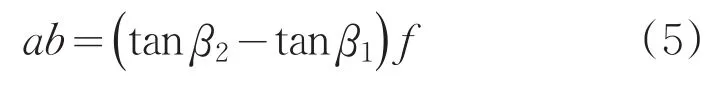
ab的中心点以O1为原点的坐标为（ff，ab 2+tanβ1˙f），此坐标为图像上提取的重心坐标。而O在CCD上的成像坐标为（f，f˙hL+f）。标定板上特征点的重心在图像上的成像点与特征点在CCD上成像求出的重心偏差为：

在该实验中r约为10mm，L约为3m，像元尺寸为3.7μm，h的取值对结果几乎无影响，这里取其最大影响值，在标定过程中α在30°到45°之间。实验结果证明：其偏差在0.05pixel以内，对标定过程几乎没有影响。

图3　标定板与CCD像面不平行

由上述实验及公式（6）的求导的结果得到最后结论：对Δ影响较大的因素是L、r和α，当α在50°到60°之间取得最大偏差值，当L远大于r时，计算结果表明其偏差几乎为0。因此，当用重心法提取特征点坐标时，一定要保证标定距离足够远。

3　改进的摄像机线性标定方法

本文改进的摄像机线性优化方法，使用线性优化方法对畸变进行矫正并未引入非线性优化方法，简化了计算。同时考虑到简便性，本文设置了主点坐标和纵横比的初始值，省去了单独标定的繁琐过程。

（1）图像的主点坐标和纵横比的标定

理想情况下，图像主点的位置在帧存图像的中心上，且光轴垂直于像面方向。实际镜头装调的过程中，因装调误差的原因，不可能实现这一点，但其主点位置会在图像帧存重心附近。针对这一点，本文将主点位置的初始值选在帧存图像的中心且取纵横比的初始值为1。

（2）求解旋转矩阵R和平移分量tx、ty

由于标定板是平面板，因此全部特征点的Zw= 0。由于仅存在径向畸变，即实际成像点与理想成像点在一条直线上，根据径向平行约束［9］：

整理得到如下矩阵形式的线性方程：

根据Tsai的两步法［1］，利用标定点的世界坐标和图像坐标利用最小二乘法原理求解超定方程的5个未知参量：

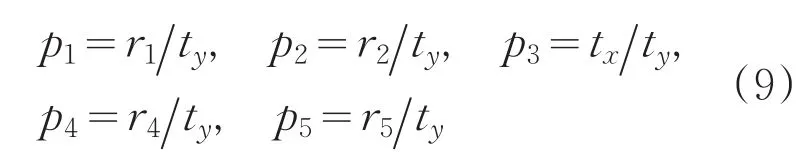
由于R是个单位正交矩阵，当p1，p2，p4，p5不两两同时为0时有：

否则t2y为其余两个参数的平方和的倒数。进而求得：（根据正交性，如果（r1r4+r2r5）为正，则在r6前加负号）。

然后根据R的单位正交性，求得r7，r8，r9：

（3）求解焦距f、一阶径向畸变系数k1和平移分量tz：

整理为含有f、k1和tz的线性方程组：

（4）求解公式的改进：

线性标定法的原理是应用最小二乘法求得近似值，公式（13）求得的结果中一阶径向畸变系数往往很小，所以f和tz的近似值相互制约，为了得到较为准确的tz以确保后续优化方案的准确性，这里镜头的焦距f取给定值25mm，此时公式（13）变为：

此时求解出k1和tz。

4　标定方法的优化

利用上述改进的线性标定方法将摄像机的大部分参数标定出来，但其内参数并未得到优化，这会严重影响标定精度，因此本文提出一种优化方法。摄像机对不同位姿的标定板进行拍照时位置保持不变，并且上述线性标定法对不同图像标定时都是以图像帧存中心为主点位置，因此虽然不同图像的世界坐标系不同，但是它们具有相同的摄像机坐标系，如图4所示。文献［10］针对这一原理将不同图像上标定点的摄像机坐标还原成在同一世界坐标系下的世界坐标这一思想可以实现，其精度主要取决于上述tz的求取准确度，因此上述线性标定法采用了固定f的方法以实现对tz的准确求取。

图4　标定板上P点的不同摄像机坐标

其标定过程如下：

公式（15）经通分整理得：

利用最小二乘法原理求解超定方程（16）。其中一共11个未知参数，因此2n必须大于11，其中n为标定点个数。

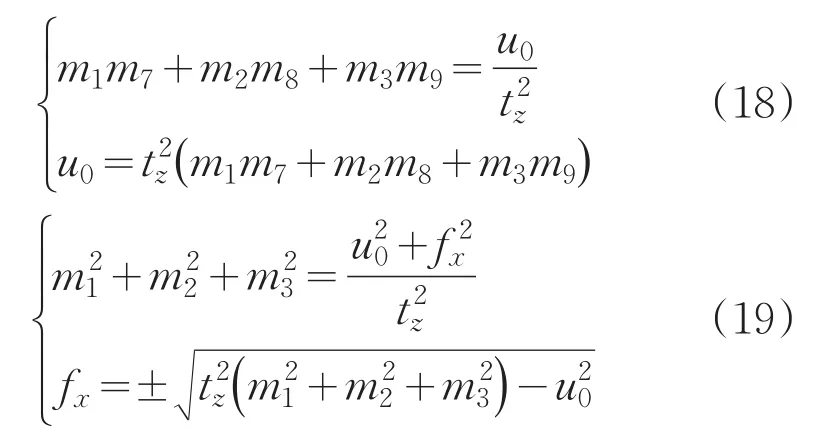
通过公式（18）和（19）可将u0和fx求解出来，其中fx取正。将求得的tz代入m7、m8和m9中，得到：

将求得的tz、u0、fx、r7、r8和r9代入m1、m2和m3中，得到：

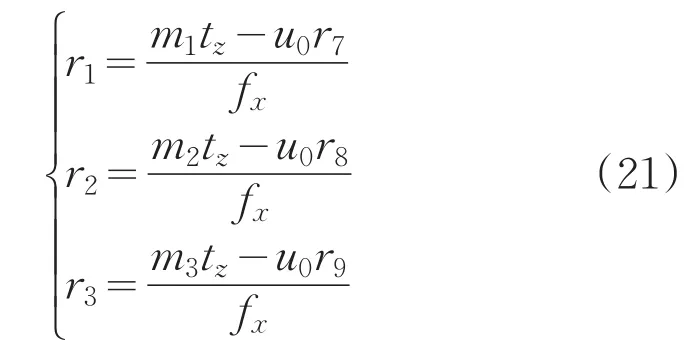
因为R是单位正交矩阵，则：

然后将求得的参数代入公式（23），得到：

最后求出tx和ty：

最后根据一阶径向畸变公式求出k，至此标定工作全部完成。

5　标定实验结果比较与分析

实验采用分辨率为1280×960像素，像元大小为3.7μm，焦距为25mm的定焦镜头。先后用Tsai两步法、张正友平面标定法、改进的线性两步标定法和本文方法对该摄像机拍摄的5幅标定板图像进行标定。如图5，为标定板上特征点的提取图像，为了评估标定其标定精度，选择每幅标定板图像上前30个特征点作为标定点，后19个点作为测试点，采用测试点的真实图像坐标与再投影后相对应的图像坐标之差的模的平均值作为标定精度的评估函数，单位为像素，公式如下：

其中（ui，vi）为测试点的真实图像坐标；（）为再投影后的图像坐标；n为测试点个数。

图5　标定板特征点提取

表1　张正友平面标定法的标定精度结果

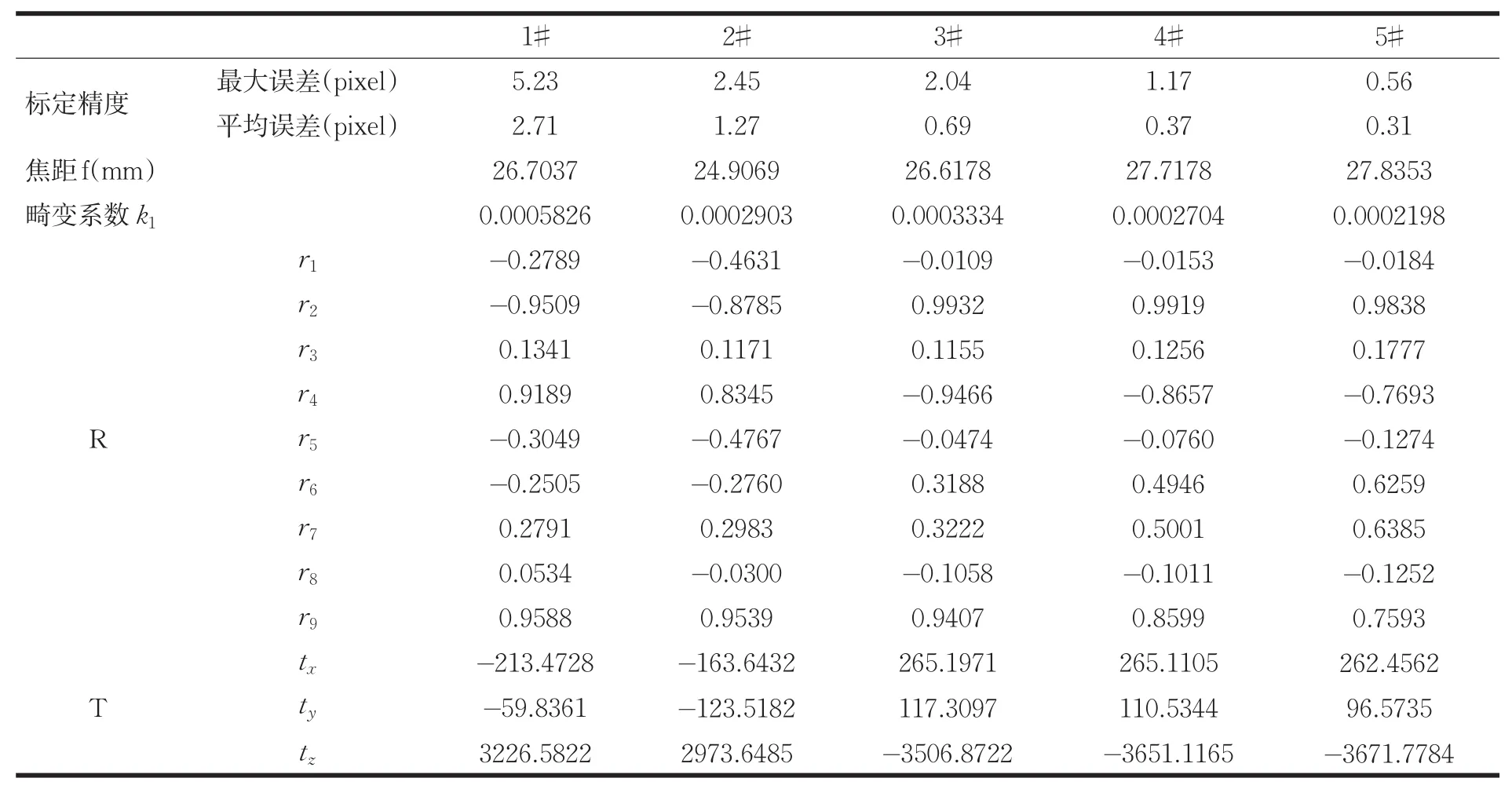
表2　Tsai两步标定法的标定精度结果

表3　线性标定结果

表4　本文的标定方法标定结果

由表（1）、表（2）、表（3）和表（4）分析可知，张正友的平面标定法和Tsai的两步法的标定精度均低于改进的线性方法和本文的标定方法；张正友的平面标定法由于标定点少，其畸变参数没有准确标定出来，其标定得到的焦距在26mm左右；Tsai的两步法其标定误差过大；线性方法其为了简便性而未对主点位置和纵横比进行标定，且焦距和畸变系数的变化幅度过大，其焦距的标准差为0.8mm，因此精度不高；而本文的标定方法，从表（4）可以看出其标定得到的内参数fx、fy、u0和v0在5次标定检测中均只有很小的变化，其焦距标定精度在0.1mm，且5次标定得到的主点位置变化在2pixel之内。足以见得，本文提出的标定方法兼容了高精度和简便性这两个特性。

6　结论

张的平面标定法对标定过程以及标定平板的要求高，导致实验复杂繁琐。Tsai的两步法是在假设主点位置和纵横比的前提下实现的，这两个关键的内参数没有标定，虽然标定过程简单但是精度受到严重影响。线性标定方法要独立的对主点位置和纵横比进行标定，这将导致一个复杂的过程，并且增加成本。本文提到的标定法同样通过对平面标定板的标定完成了对其内外参数的优化，且其方法简单，标定精度高。其不足之处在于：它对特征点的标定误差受到改进的线性标定方法的约束，没有得到较之明显的提高，这是后续需要继续改进的地方。

［1］马颂德，张正友.计算机视觉［M］.北京：科学出版社，1998.

［2］Y I Abdel-Aziz，H M Karara.Direct linear transformationfromcomparatorcoordinatesintoobject spacecoordinatesinclose-rangephotogrammetry［C］.In：Proceedings of the ASP Symposium on Close-Range Photogrammetry，Urbana，Illinois，1971：1-18.

［3］吴福朝，阮宗才.非线性模型下的摄像机自标定［J］.计算机学报，2002，25（3）：16-19.

［4］Roger Y，TSAI.A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV camera and lenses［J］. IEEE Journal of Robotics and Automation，1987，3（4）：323-334.

［5］Zheng-you ZHANG.A flexible new technique for camera calibration［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（11）：1330-1334.

［6］申琳.改进的摄像机线性标定方法研究［D］.吉林：长春理工大学，2011.

［7］冯翔.复杂三维模型相似性研究［D］.北京：北京师范大学计算机应用技术，2009.

［8］徐杰.机器视觉中摄像机标定Tsai两步法的分析与改进［J］.计算机工程与科学，2010，32（4）：46-47.

［9］邹凤娇，苏显渝，李美菊.基于共面点的摄像机线性标定法［J］.光电工程，2006，32（4）：37-41.

［10］杨博文，张艳丽，叶南，等.面向大视场视觉测量的摄像机标定技术［J］.光学学报，2012，9（32）：0915001—1-0915001—7.

Improved Camera Linear Calibration Optimization Method

LIU Boyu，ZHAO Yang，YANG Jinhua
（School of Optoelectronic Engineering，Changchun University of Science and Technology，Changchun，130022）

At present，the commonly used camera calibration methods do not have a good convergence of high accuracy and simplicity.In view of this，this paper proposes a new method of calibration optimization.Considering the simplicity，the calibration method of this paper selects the position of principal point which is on the center of the image and aspect ratio which is 1 as the initial condition.Then we use improved camera linear calibration method to obtain all points’coordinates of different images in the same camera coordinate system；finally，using the 3D points in the camera coordinate system to optimize the internal and external parameters.The experimental results show that the focal length’s error was less than 0.1mm，the maximum error of the principal point’s position is about 2 pixel，the maximum error of the test points is less than 0.5pixel and the calibration method which is proposed in this paper is a simple and accurate calibration method.

camera calibration；camera model；linear calibration

TP391

A

1672-9870（2016）04-0090-07

2016-03-12

刘博宇（1992-），男，硕士研究生，E-mail：751892260@qq.com

杨进华（1969-），男，教授，E-mail：yangjh@cust.edu.cn