基于最小二乘支持向量机的油页岩含油率近红外光谱分析

张福东, 刘　杰, 王智宏

(吉林大学仪器科学与电气工程学院, 长春 130021)



基于最小二乘支持向量机的油页岩含油率近红外光谱分析

张福东, 刘杰, 王智宏

(吉林大学仪器科学与电气工程学院, 长春 130021)

为了提高油页岩含油率近红外光谱分析建模的预测精度和稳定性, 开展了基于最小二乘支持向量机(LS-SVM)建模方法的对比研究. 采用主成分-马氏距离(PCA-MD)和基于蒙特卡洛采样(MCS)2种方法进行了奇异样本的检测, 采用径向基核函数的LS-SVM、 偏最小二乘(PLS)和反向传播神经网络(BPANN)3种方法进行建模方法对比. 结果表明, 对于64个油页岩岩芯样本, 与PCA-MD方法相比, 采用MCS方法剔除奇异样本后所建PLS模型的预测精度提高了28%. 对于MCS方法剔除奇异样本后的58个样品, 采用Kennard-Stone法划分了44个样品的校正集和14个样品的预测集, 采用2阶导数和标准化预处理方法, 建立了100个LS-SVM的校正模型, 模型的预测决定系数R2平均值达到0.90以上, 高于PLS和BPANN模型的对应值; 且R2的变化量(0.02)小于BPANN模型的对应值(0.32). 因此, MCS奇异样本检测结合LS-SVM方法可提高油页岩含油率样本建模的精度和稳定性.

最小二乘支持向量机; 油页岩; 含油率; 近红外光谱分析; 奇异样本

油页岩资源作为非常规石油资源, 因其储量丰富、 具有开发应用潜力, 且开采技术不断成熟而受到极大关注[1～3]. 油页岩(又称油母页岩)是一种高灰分的固体可燃有机沉积岩, 热解可产生油母, 油母(也称为页岩油)主要由碳、 氢、 氧及少量的硫和氮元素组成. 含油率是油页岩中页岩油所占的质量分数, 是油页岩最重要的评价指标. 含油率的标准测量方法是低温干馏法(SH/T 0508-92), 此法需要在实验室进行高温热解, 过程繁琐且效率低, 严重制约了油页岩资源勘查和开采的效率[4]. 目前, 油页岩开发利用亟需在线或现场分析技术对大量样品进行测试.

近红外光谱分析技术具有快速、 高效和无损等特点[5], 将其与化学计量学方法结合可实现物质的定性和定量分析, 已在农业、 食品、 化工和医药等领域被广泛应用[6]. 2002年, Romeo等[7]等首次使用近红外光谱技术获取了澳大利亚中昆士兰地区的油页岩样本的光谱数据, 采用多元散射校正(MSC)和二阶导数预处理方法, 并结合偏最小二乘(PLS)回归算法建立了油页岩校正模型, 证明了近红外光谱技术可用于预测油页岩含油率. 我们[8]研究了不同的光谱数据形式、 4种不同的建模区间以及11种数据预处理方法对PLS模型精度的影响. 但以上研究均未考虑奇异样本的存在, 在近红外光谱分析油页岩含油率过程中, 因为样品组分异常以及仪器的随机误差等会产生奇异样本, 奇异样本的存在会使基于偏最小二乘建立的模型不稳健, 很难准确地评价所建模型. 赵振英等[9]研究了漫反射近红外光谱分析油页岩含油率过程中奇异样本的识别和剔除方法, 发现主成分-马氏距离(PCA-MD)分析方法可有效地识别奇异样本并提高分析模型的预测能力. PLS方法是基于线性回归方式的多元校正方法, 而近红外光谱数据与浓度之间通常是非线性关系, 从而导致无法获得理想的校正模型. 我们[10,11]将神经网络方法应用于油页岩含油率的预测, 发现采用反向传播神经网络(BPANN)方法的建模精度略优于PLS方法, 但模型的预测决定系数最大为0.85, 而且所建模型的稳定性较差, 30次BPANN所建模型的决定系数平均值为0.59, 无法满足实际分析的精度要求. 以上方法推动了油页岩含油率快速检测技术的应用, 但仍存在模型精度低和稳定性差等问题, 而模型的预测决定系数需至少达到0.90, 预测结果才可以被接受[12], 因此需选择合适的多元校正方法使模型预测决定系数达到0.90以上.

支持向量机(SVM)是基于统计学习理论的机器学习方法[13,14], 它以核函数和结构风险最小化原则为基础, 采用优化算法训练得到一个具有最大边界的模型, 以提高模型的泛化能力. SVM回归方法的核心思想是通过选定的核函数将非线性问题映射到高维特征空间的线性问题. 与基于经验风险最小化原则的人工神经网络(ANN)方法相比, SVM不仅结构简单, 而且能够较好地解决小样本、 非线性以及高维数等问题. 目前, SVM回归算法已广泛应用于水文地质[15]、 化学[16]和农业[17,18]等领域. 本文针对使用自主研制的光谱仪获取的吉林扶余油页岩科研基地2号钻井(FK2)岩芯样品数据所建模型精度偏低的问题, 基于预测残差和蒙特卡洛采样方法的奇异样本检测方法[19,20]识别奇异样本, 以确保所建模型的稳健性, 并采用二阶导数+标准化的组合预处理方法, 开展最小二乘支持向量机(LS-SVM)、 PLS和ANN建模分析对比研究, 以确定LS-SVM方法是否适合油页岩含油率的快速分析.

1　实验部分

1.1仪器

自主研发的油页岩现场近红外光谱(PISA-OS)仪[21], 采用光栅扫描分光原理, 探测器为制冷PbS, 波长范围1300～2500 nm, 光谱信噪比为2000@1600 nm, 采样间隔1～8 nm可选, 取样方式: 积分球/光纤取样, 光谱数据形式: 反射率、 吸光度和K-M函数可多选.

1.2样品

油页岩样品来自吉林扶余扶科油页岩基地, 取2号钻井359.7～390.8 m深处的岩芯, 间隔0.1～0.5 m为一段, 每段内均匀取样装袋, 共65袋样品, 恒温干燥24 h. 将样品粉碎后每袋取200 g, 用低温干馏法测焦油产率Tar.ad(%), 范围0.45%～10.87%, 平均值3.33%, 标准偏差1.92%.

1.3光谱数据采集

Fig.1　Original NIR spectra of 58 oil shale samples

每袋样品取3块, 选择一处较平整面置于PISA-OS仪的测样窗口, 测量其相对参比(参比为镀金白板)的吸光度, 采样间隔为2 nm, 每袋样品得到3个光谱数据, 取平均值得到样品的吸光度数据, 如图1所示.

1.4建模方法对比

1.4.1模型试建PLS建模: 为了选取PLS建模的最佳潜变量数, 首先对光谱数据和含油率数据分别进行标准化预处理, 然后设置重复双重交叉校验(RDCV)方法的初始参数, 最大潜变量数A为10, 校验方法为5折交叉校验, 蒙特卡洛采样次数N为200, 利用设置好的重复双重交叉校验方法对油页岩样品进行PLS建模, 统计各子模型所选取的最优模型主成分数以及模型预测标准偏差RMSEP, 选取出现频次最高的潜变量数为PLS建模的最佳潜变量数Aopt.

BPANN建模[22,23]: 为了选取BPANN建模的最佳隐含层节点数, 采用上述PLS建模中的预处理方法, 以及选取的最佳潜变量数作为主成分分析(PCA)的最佳主成分数, 构建3层BPANN, 输入层节点数为采用PCA的得分作为输入变量, 输出层节点数为1, 选取预测误差均方根较小的传递函数组合为“tansig”和“purelin”, 训练函数为“traniscg”, 训练迭代次数为300. 设置隐含层节点数P范围为5～30, 利用网格寻优的方法进行5次BPANN建模, 计算5次平均的RMSEPi, 选取RMSEPi最小对应的节点数为BPANN建模的最佳节点Popt.

1.4.2奇异样本剔除方法对比主成分-马氏距离(PCA-MD)方法: 采用1.4.1节PLS建模中的方法预处理后, 利用PCA-MD检测奇异样本, 计算Aopt的马氏距离, 剔除马氏距离>3Aopt/n(其中n为样本数)的奇异样本.

基于预测残差和蒙特卡洛采样(MCS)方法: 采用1.4.1节PLS建模中的方法预处理后, 设置 MCS方法的参数, 最佳潜变量为Aopt, 采样次数为2000, 随机选取75%的校正集. 运行此算法, 得到预测残差均值-方差分布图. 采用硬阈值方法, 参考文献[19,20]并根据经验设置阈值参数分别为残差均值和方差均值的0.75倍, 依据阈值参数剔除奇异样本.

分别利用2种分析方法剔除奇异样品后的数据库, 采用1.4.1节PLS建模中的预处理方法, 建立PLS回归模型, 通过模型统计参数(RMSEP和R2)的对比分析, 评价2种奇异样本剔除方法的优劣.

1.4.3数据预处理及校正集选取光谱预处理: 为了消除光谱噪声和基线漂移等问题, 分析了不同预处理方法的效果, 经过反复验证, 采用一阶导数对光谱数据进行预处理, 然后分别对光谱数据和含油率数据进行标准化处理.

校正集选取: 采用Kennard-Stone(KS)法划分75%样本作为校正集, 剩余25%样本作为预测集. KS算法[24,25]基于变量之间的欧式距离, 在特征空间里均匀地选取样本, 使划分到的校正集代表性较强, 而且其不受样本数量的限制, 因此能有效地改善模型的预测能力.

1.4.4建模方法及模型对比建模方法: PLS方法是应用最广泛的线性校正方法, 选取最佳潜变量数的变量建立回归方程, 通过交叉验证方法来防止过拟合现象, 具有建模速度快、 优化参数少的优势. BPANN方法基于误差反向传播的多层前向神经网络, 需要依据所解决的问题的复杂度、 样本集大小等选取合适的层数、 学习算法以及误差函数等, 通过网络训练优化相应参数, BPANN方法较PLS方法训练过程复杂, 优化的参数较多. LS-SVM方法具有结构简单, 可以避免神经网络结构选择和局部极小点问题, 适合处理高维数小样本数据, 需要依据不同问题选取合适的核函数, 优化相应的核函数参数使模型具有更高的精度和泛化能力.

建模过程: 为了对比3种多元校正方法对油页岩样品所建模型的预测精度和稳定性, 分别对PLS建立1个模型, 对BPANN和LS-SVM 2种方法分别随机建立100个模型. 利用1.4.1节中PLS试建时选取的Aopt, 对校正集建立PLS回归模型, 得到PLS模型统计参数; 利用1.4.1节中选取的Popt以及BPANN初始参数对校正集进行100次BPANN建模, 得到BPANN模型统计参数; 采用了径向基(RBF)核函数, 使用模拟退火算法优化LS-SVM参数(正则参数gama和平方带宽sig2), 然后用最优参数建立LS-SVM的回归模型, 重复此过程100次, 得到LS-SVM模型的统计参数.

2　结果与讨论

2.1PLS和BPANN回归模型试建

Fig.2　Frequency distribution of the optimum latent variable number of components based on RDCV method

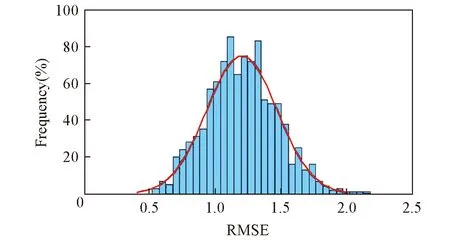
Fig.3　　　　Frequency distribution of the RMSEP of oil yield for oil shale

采用RDCV方法进行PLS模型试建, 得到的最优模型最佳潜变量数的最高频度值分布和RMSEP的分布如图2和图3所示. 由图2可知, 出现频次最高的潜变量数为5, 表明PLS所建模型的Aopt为5. 由图3可知, 所有样本参与建模的RMSEP分布在0.5～2之间, 其平均值为1.20, 表明模型预测精度很低, 可能存在奇异样本, 因此需进行奇异样本检测.

为了降低过拟合的风险, 设置BPANN试建模的训练目标的均方误差为0.01, 然后采用BPANN校正方法建立模型选取Popt, 得到模型平均的RMSEPi最小对应的节点数为7, 表明Popt选择7最佳.

2.2奇异样本剔除

采用了PCA-MD诊断方法, 计算得出Aopt下所有样品的马氏距离, 以及界定奇异样本的阈值, 进行归一化处理后如图4所示. 图4中直线为阈值界限, 阈值为0.5548. 超出阈值范围的样品有37, 61和20号样品. 采用了蒙特卡洛奇异样本检测分析方法, 计算得到所有样品的预测残差的均值和标准偏差, 经归一化处理后如图5所示. 由图5可见, 部分样本位于高均值或者高标准差的区域, 属于奇异样品, 计算得出预测残差均值阈值和均方根阈值分别为0.7500和0.7500. 超出阈值的样本被认定为奇异样本, 经统计为37, 61, 12, 33, 35, 14和27号样品. 由PCA-MD和MCS 2种方法均诊断出37和61号样品(图1中加号虚点线), PCA-MD方法诊断出的其余样品为20号(图1中圆点虚线), 而MCS方法诊断出的其它样品为12, 33, 35, 14和27(图1中方形虚线). 由图1可知, 37号样品光谱明显偏离, 与检测方法一致, 而其它被诊断出的奇异样本无法直接判断. 因此, 利用2种方法剔除异常样品后的数据库进行PLS建模. 由图6和图7可知, 利用1.4.1节中相同的过程建立PLS模型后, 经PCA-MD剔除异常样本后所有样本建模的RMSEP在0.8～1.5之间, 其预测误差平均值为1.17; 而经MCS剔除异常样本后所有样本建模的RMSEP在0.6～1之间, 其平均值为0.84. 以上结果表明, 与PCA-MD方法相比, 采用MCS方法剔除奇异样本后所建PLS模型的预测精度提高了28%. 因此, 将MCS方法所选取的奇异样本均从数据库中剔除, 可得到共58个新的建模样本.

Fig.4　　　　MD values between each sample spectrum and the center of spectra of all samples

Fig.5　　　　Result of variance of residuals versus mean of residuals on oil shale data

Fig.6　　　　Frequency distribution of the RMSEP for oil shale data using PCA-MD

Fig.7　　　　Frequency distribution of the RMSEP for oil shale data using MCS

2.3数据集划分

采用KS算法按照3∶1比例划分样品, 得到44个校正集样本和14个预测集样本, 表1列出了数据集的统计结果. 可见, 校正集的含油率含量的最大值大于预测集中的最大值, 而校正集的含油率含量的最小值小于预测集中的最小值, 并且校正集的标准偏差和变异系数均比预测集的大. 此结果表明, 校正集含量分布比较分散, 所选样本具有一定的代表性.

Table 1　Statistical results of the oil yield in the oil shale samples

2.4三种校正方法的模型对比

2.4.1PLS和BPANN模型结果PLS建模: 经试建模得到PLS的最佳潜变量数为5. 由表2可见, 采用一阶导数+标准化的预处理后建立的PLS模型的RMSEP为0.36,R2为0.85, 表明PLS所建模型的预测精度较低.

Table 2　Prediction results for the oil yield in the oil shale samples

Fig.8　　　　RMSEP distribution of 100 runs results for BPANN

Fig.9　　　　RMSEP distribution of 100 runs results for LS-SVM

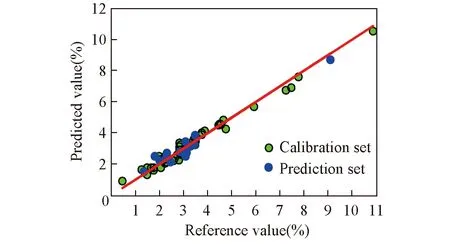
Fig.10　　　　Predicted value vs. reference value of oil yield for optimal LS-SVM model

2.5模型结果讨论

对于单次最优建模条件, BPANN方法最优, 其基于经验风险最小化原则, 利用正则化方法和提前停止法在一定程度上提高了神经网络的预测精度; LS-SVM方法基于结构风险最小化原理, 利用模拟退火算法提高了模型的泛化能力和稳定性; PLS建模基于光谱数据和目标分析物性质之间的方差最大化原则, 由于油页岩样品性质的复杂化以及模型的非线性问题使PLS方法建模精度略低, 而且易受奇异样本的影响, 但其建模速度快. 对于多次建模条件, LS-SVM方法最优, BPANN方法在一定程度上提高了模型的预测精度, 但由于利用经验最小化原则, 过分强调得到较小的训练误差, 导致模型的稳健性和泛化能力有所降低. LS-SVM基于统计学习理论, 利用高斯径向基核函数使其模型结构简单, 而且通过模拟退火算法优化LS-SVM模型参数获取最优模型不仅提高了模型的泛化能力, 并且增强了模型的稳健性. 因此, 对于小样本复杂的油页岩样品体系, 正好与LS-SVM方法在小样本、 非线性及高维数等实际问题中应用效果较好相吻合.

3　结　　论

针对油页岩近红外光谱分析建模中的预测精度低和稳定性差的问题, 对比研究了PCA-MD和MCS奇异样本检测方法, 发现MCS方法可有效剔除油页岩样本中的7个奇异样本, 所建PLS模型精度提高了28%. 采用 2阶导数对光谱数据进行预处理, 以标准化对光谱数据和含油率数据进行处理, 利用径向基核函数的LS-SVM算法建立了校正模型. 与PLS校正方法相比, LS-SVM方法所建模型的精度比PLS高, 达到了0.90以上; 与BPANN校正方法相比, LS-SVM方法的最优模型的精度比BPANN低, 但100个LS-SVM模型的精度平均值比BPANN高, 精度平均值达到90%以上, 而且100个LS-SVM模型的ΔR2(0.02)明显低于BPANN(0.32). 因此, 对于油页岩含油率近红外光谱分析而言, MCS奇异样本检测结合LS-SVM建模方法具有很高的建模的精度和稳定性.

[ 1 ]Hou J. L., Ma Y., Li S. Y., Teng J. S.,Chem.Ind.Eng.Prog., 2015, 34(5), 1183—1190(侯吉礼, 马跃, 李术元, 藤锦生. 化工进展, 2015, 34(5), 1183—1190)

[ 2 ]Zhao Z. Y., Lin J., Yu Y.,Chem.Res.ChineseUniversities, 2015, 31(3), 352—356

[ 3 ]Kristin N. A., Dinesh R. K., Kalpana S. K.,SpectrochimicaActaPartAMolecular&BiomolecularSpectroscopy, 2012, 89(89), 105—113

[ 4 ]Mike J. A., Firas A., Suresh B., Stephen G.,Fuel, 2005, 84(Suppl.14/15), 1986—1991

[ 5 ]Luypaert J., Massart D. L., Heyden Y. V.,Talanta, 2007, 72(3), 865—83

[ 6 ]Chu X. L.,J.NearInfraredSpec., 2015, 23(5), v—vii

[ 7 ]Melissa J. R., Michael J. A., Andrew R. H.,J.NearInfraredSpec., 2002, 10(3), 223—231

[ 8 ]Wang Z. H., Liu J., Wang J. R., Sun Y. Y., Yu Y., Lin J.,J.JilinU.Techno.Ed., 2013, 43(4), 1017—1022(王智宏, 刘杰, 王婧茹, 孙玉洋, 于永, 林君. 吉林大学学报: 工学版, 2013, 43(4), 1017—1022)

[ 9 ]Zhao Z. Y., Lin J., Zhang H. Z.,Spectrosc.Spect.Anal., 2014, 34(6), 1707—1710(赵振英, 林君, 张怀柱. 光谱学与光谱分析, 2014, 34(6), 1707—1710)

[10]Li S. Y., Ji Y. J., Liu W. Y., Wang Z. H.,Spectrosc.Spect.Anal., 2013, 33(4), 968—971(李素义, 嵇艳鞠, 刘伟宇, 王智宏. 光谱学与光谱分析, 2013, 33(4), 968—971)

[11]Liu J., Zhang F. D., Teng F., Li J., Wang Z. H.,Spectrosc.Spect.Anal., 2014, 34(10), 2779—2784(刘杰, 张福东, 滕飞, 李军, 王智宏. 光谱学与光谱分析, 2014, 34(10), 2779—2784)

[12]Kim K., Lee J. M., Lee I. B.,Chemometrics&IntelligentLaboratorySystems, 2005, 79(1/2), 22—30

[13]Olivier D., Cyril R., Alexandra D., Ludovic D.,Chemometrics&IntelligentLaboratorySystems, 2009, 96(1), 27—33

[14]Suykens J. A. K., Gestel T. V., Brabanter J. D.,LeastSquaresSupportVectorMachines, World Scientific, Singapore, 2002, 1—24

[15]Sujay R. N., Paresh C. D.,AppliedSoftComputing, 2014, 19(6), 372—386

[16]Li H. D., Liang Y. Z., Xu Q. S.,Chemometrics&IntelligentLaboratorySystems, 2009, 95(2), 188—198

[17]Xie Q. Y., Huang W. J., Liang D., Peng D. L., Huang L. S., Song X. Y., Zhang D. Y., Yang G. J.,Spectrosc.Spect.Anal., 2014, 34(2), 489—493(谢巧云, 黄文江, 梁栋, 彭代亮, 黄林生, 宋晓宇, 张东彦, 杨贵军. 光谱学与光谱分析, 2014, 34(2), 489—493)

[18]Zhang H. Y., Peng Y. K., Wang W., Zhao S. W., Liu Q. Q.,Spectrosc.Spect.Anal., 2012, 32(10), 2794—2798(张海云, 彭彦昆, 王伟, 赵松玮, 刘巧巧. 光谱学与光谱分析, 2012, 32(10), 2794—2798)

[19]Cao D. S., Liang Y. Z., Xu Q. S., Li H. D.,JournalofComputationalChemistry, 2010, 31(3), 592—602

[20]Liu Z. C., Cai W. S., Shao X. G.,ScienceinChinaSeriesB:Chemistry, 2008, 51(8), 751—759

[21]Wang Z. H., Lin J., Wu Z. Y., Zhu H., Zhan X. X.,ChineseJournalofScientificInstrument, 2005, 26(11), 1135—1138, 1154(王智宏, 林君, 武子玉, 朱虹, 占细雄. 仪器仪表学报, 2005, 26(11), 1135—1138, 1154)

[22]Shan H. Y., Fei Y. Q., Huan Y. F.,Chem.Res.ChineseUniversities, 2014, 30(4), 582—586

[23]Zhang H., He Y. H., Tang D., Li Y. W.,Chem.J.ChineseUniversities, 2014, 35(6), 1199—1203(张汇, 何玉韩, 唐铎, 李彦威. 高等学校化学学报, 2014, 35(6), 1199—1203)

[24]Kennard R. W., Stone L. A.,Technometrics, 1969, 11, 137—148

[25]Pravdova V., Walczak B., Massart D. L.,AnalyticaChimicaActa, 2002, 456(1), 77—92

(Ed.: N, K)

† Supported by the National Potential Oil and Gas Resources(Oil Shale Resources Exploration and Exploitation) Research Cooperation Innovation Project of China(No.OSR-02-04) and the Jilin Provincial Science and Technology Development Major Science and Technology Project, China(No.20116014).

Analysis of Oil Yield from Oil Shale Minerals Based on Near-infrared Spectroscopy with Least Squares Support Vector Machines†

ZHANG Fudong, LIU Jie, WANG Zhihong*

(CollegeofInstrumentationScience&ElectricalEngineering,JilinUniversity,Changchun130021,China)

In order to improve the prediction accuracy and precision of near-infrared(NIR) spectroscopy model for analyzing the oil yield from oil shale, sixty-four oil shale samples from the No.2 well drilling of Fuyu oil shale base were analyzed based on least squares support vector machines(LS-SVM) calibration models. The Principal component-mahalanobis distance(PCA-MD) method and the Monte-Carlo sampling-based detection of outliers(MCS) method were investigated as means of removing the outliers. The modeling methods of radial basis function-based LS-SVM, partial least squares(PLS) and back propagation neural network (BPANN) were compared. The results showed that, compared with PCA-MD, the prediction accuracy of PLS models based on MCS was improved by 28%. The samples after eliminating the outliers were divided into the calibration set with 44 samples and the prediction set with 14 samples using the Kennard Stone method. One hundred LS-SVM calibration models were established based on preprocessing method of second-derivative and autoscaling. The mean determination coefficient(R2) were more than 90% and higher than PLS and BPANN models, and the fluctuation ofR2were less than BPANN models. Thus, LS-SVM regression with MCS method can improve the accuracy and precision of oil yield of oil shale modeling.

Least squares support vector machine; Oil shale; Oil yield; Near-infrared spectroscopy; Outlier

10.7503/cjcu20160344

2016-05-16. 网络出版日期: 2016-09-20.

国家潜在油气资源(油页岩勘探开发利用)产学研用合作创新子课题(批准号: OSR-02-04)和吉林省科技发展计划项目重大科技专项(批准号: 20116014)资助.

O657.33

A

联系人简介: 王智宏, 女, 博士, 教授, 博士生导师, 主要从事近红外光谱仪器研制及应用技术研究.E-mail: zhwang@jlu.edu.cn.