一种基于正交匹配追踪的压缩感知信号检测算法*
2016-11-02秦国领李梓博
秦国领,郑 森,王 康,李梓博
一种基于正交匹配追踪的压缩感知信号检测算法*
秦国领**1,郑 森1,王 康2,李梓博3
(1.酒泉卫星发射中心,甘肃酒泉 732750;2.西昌卫星发射中心,四川西昌 615000;3.解放军63778部队,黑龙江佳木斯 154002)
针对当前压缩感知信号检测算法没有充分利用稀疏系数幅值信息的不足,提出了一种新的检测算法。从正交匹配追踪算法切入,通过深入分析归一化残差的变化信息,提出归一化余差概念,建立了一种基于归一化残差和归一化余差二维判决的信号检测算法。仿真结果表明,算法的有效检测阈值区间随着信噪比的降低而不断减小,且在信噪比为-8 dB、压缩比为0.25时,该算法的检测概率仍能满足要求,具备较好的适应性。
压缩感知;信号检测;正交匹配追踪;特征量
1 引 言
Nyquist采样定理规定只有采样频率大于或等于2倍信号带宽时才能避免信号频谱的混叠,这无疑对信息采样、传输和处理挑战很大。压缩感知[1],又称“压缩传感”,是一种有别于Nyquist采样定理的采样方法。该理论指出[2]:如果信号在某变换域是稀疏的或可压缩的,则可利用线性非自适应运算将信号转化为低维观测向量,并通过求解稀疏最优化问题将原始信号高概率的精确重建,这将有力缓解海量数据实时处理的压力。
当前,信号和图像的重构及其相关问题是压缩感知研究的重点内容[3-4]。但对于只需从采样数据中提取某些特征信息的压缩感知信号,精确重构信号既不经济也不必要。如信号检测,其重点在于检测目标信息而不是实现信号重构。文献[5]论证了基于压缩感知的信号检测无需信号重构便可实现信号检测。文献[6]提出一种基于匹配追踪(Matching Pursuit,MP)的信号检测算法,通过从压缩感知信号的采样数据中提取特征值,实现了信号检测。文献[7]针对MP算法特征量波动量大的不足提出一种正交匹配追踪(Orthogonal Matching Pursuit,OMP)检测算法,有效改善了特征量的波动。文献[8]利用归一化残差作为特征信息,提出了一种基于归一化残差的OMP算法,在维持OMP算法检测性能的同时有效降低了OMP算法的运算量。然而,文献[7-8]算法在低信噪比下的检测性能不能满足指标要求。针对这个问题,本文提出一种归一化残差和归一化余差相结合的信号检测算法。仿真结果表明,该算法在相同信噪比下,检测概率高;相同检测概率下,所需的采样点数少。
2 基于归一化残差的压缩感知信号检测算法
2.1压缩感知理论
压缩感知理论主要涉及稀疏分解、压缩测量和信号重构3个方面的内容。设信号x∈ RRN×1为N×1维的离散序列,ΨT=[φ1,φ2,…,φm,…,φN]为 RRN空间N×N维的基矩阵,信号x可表示为[9]

式中:Ψ为稀疏基矩阵;θ为系数向量,且ΨΨT=I,θk=〈x,Ψk〉。若θ是K稀疏的,则可构建一个与稀疏基Ψ不相关的测量矩阵Φ,实现信号x的降维观测[10]:

式中:y为压缩测量值;Φ为测量矩阵;M/N为压缩比,且M< 为了确保y值能够精确重构信号x,ΘM×N需要满足约束等距性,即 最终利用1-范数可获得信号x的最优解为 2.2信号检测原理 信号检测主要是为了区分两种情况: 式中:s为目标信号;n为噪声。 由于目标信号具备稀疏性,而高斯白噪声不具备稀疏性,因此检测问题又可以描述为下面两种情况: 式中:Ψs为s对应的稀疏基。 由式(6)可知,检测信号是否存在可通过判断θs是否存在来区别,即 然而,直接利用特征值θs是否为0进行信号检测可能会受到噪声因素的影响,因此常将θs通过与设定的门限阈值进行比较,实现信号有无的判断。 2.3基于归一化残差的信号检测算法 文献[8]通过一次迭代提取归一化残差信息,并与门限阈值进行比较,实现信号检测。该算法的具体描述如下: (1)初始化 初始残差r_n=y,变量矩阵Aug_t=[]赋空; (2)确定内积最大值 残差r_n与Θ的所有列向量Θi分别求内积,确定内积最大值,即nt= argmaxj=1,2,…,N| (3)更新变量矩阵 对应更新变量矩阵Aug_t=[Aug_t,Θnt],并对nt的对应列Θnt赋空; (4)计算稀疏系数 利用最小二乘方法计算稀疏系数λ=(Aug_tT*Aug_t)-1*Aug_tT*y; (5)确定估计值 通过稀疏系数以及变量矩阵确定本次估计值:r=Aug_t*λ; (6)更新残差 计算新的残差r_n=y-r; (7)归一化残差 计算归一化残差值η=‖r_n‖2/‖y‖2; (8)信号检测判别 如果归一化残差小于阈值,即η<σ,则选择H1,否则选择H0。 3.1改进算法分析 归一化残差定义为信号重构时每次迭代后剩余能量与总能量的比值: 设信号x是离散序列,Ω=[Ω1,Ω2,…,Ωi,…,ΩN]T是空间N×N维的稀疏基,Γ=[Γ1,Γ2,…,Γi,…,ΓN]是与Ω不相关的测量矩阵,且‖Γi‖2=1,y为相应的压缩测量值,存在 式中:a为系数向量,ai=〈x,Ωi〉。 确定向量a中绝对值最大的元素及其相应位置: 式中:max(x)为取向量x中最大的元素;abs(x)为对向量x的每个元素求绝对值;location(v)为取元素v在相应向量中的位置。 首次迭代后的归一化残差为 由式(12)可知,归一化残差是通过对稀疏系数幅值平方运算后的线性计算得到,考虑到因素k的存在,归一化残差的斜率变化较小,因此归一化残差能够克服稀疏系数幅值波动大的不足。但是,归一化残差是基于迭代的最大稀疏投影系数得到,本质上是OMP算法的改进,缺乏信号能量信息的充分挖掘。 本文通过引入归一化余差概念来提高检测效果。归一化余差定义为连续二次残差能量的变化与总能量的比值: 设u和L2是向量a中绝对值第二大的元素及其对应的位置,则首次和二次迭代确定的归一化余差为 由于目标信号和噪声在稀疏基上的稀疏性不同,因此信号和噪声迭代计算时稀疏系数的大小不同。如果稀疏基是基于目标信号构造的,当目标信号存在时,由于稀疏基中存在目标信号,首次迭代和二次迭代产生的稀疏投影系数差别很大,归一化余差和归一化残差之和远小于1;当只有噪声存在时,考虑到噪声对于稀疏基的非稀疏性,首次迭代和二次迭代产生的稀疏投影系数差别较小。因此,归一化余差和归一化残差之和接近1。 通过分析可知,归一化残差和归一化余差显示了迭代残留能量的变化规律,且目标信号存在与否时归一化残差与归一化余差之和与1的关系变化很大。因此,可利用归一化残差与归一化余差的数值关系来实现信号的检测。 3.2改进算法流程 通过前文分析,可确定改进算法的检测流程如图1所示。改进算法与归一化残差算法的主要区别:一是首次归一化余差是基于第一次和第二次迭代运算获得的,因此算法一共需要进行两次迭代;二是算法的判决门限增加,由基于归一化残差的一维判决转化为基于归一化残差和归一化余差相结合二维判决。 图1 改进算法的信号检测流程图Fig.1 The signal detection flowchart of improved algorithm 实验选择雷达领域常用的单分量线性调频(Linear Frequence Modulation,LFM)信号为目标信号,假定混频后载波频率为25 MHz,调频斜率为75 MHz/μs,采样频率fs=250 MHz,脉宽T=2 μs,采用构建的波形匹配稀疏基,初始频率搜索范围为1~50 MHz,搜索步长为1 MHz,调频斜率搜索范围设定为51~100 MHz/μs,搜索步长为1 MHz/μs,在构建原子字典中原子数目共2 500个,基于Nyquist采样定理的采样点数为N=512;在实验中,先验概率P(H0)=P(H1)=0.5,为提高统计的准确度,将检测概率定义为1 000次检测对应的统计结果;同文献[7]规定,只有当检测概率大于0.95时,检测才有意义。 4.1归一化残差和归一化余差与迭代次数的数值关系 参数方面,观测点数为M=N/4,在SNR=10 dB、SNR=5 dB、SNR=0 dB和SNR=-5 dB 4种典型情况下,目标信号存在和不存在时,归一化残差和归一化余差与迭代次数的变化曲线如图2和图3所示。 图2 归一化残差与迭代次数的变化关系Fig.2 The relation between normailized residual and iterative number 图3 归一化余差与迭代次数的变化关系Fig.3 The relation between normailized remainder and iterative number 通过分析图2和图3可知: (1)当目标信号不存在时,首次迭代的归一化残差远大于目标信号存在时的归一化残差,且SNR越大,归一化残差越小,即使低信噪比下(SNR= -5 dB)首次迭代的归一化残差仍小于0.75; (2)目标信号存在时首次迭代的归一化余差远大于目标信号不存在时的归一化余差,且SNR越大,归一化余差越小,低信噪比下(SNR=-5 dB)归一化余差仍小于0.028; (3)目标信号存在时的首次归一化残差与首次归一化余差之和小于0.76,且信噪比越大,归一化残差与归一化余差之和越小; (4)当只有噪声存在时的首次归一化残差与首次归一化余差之和大于0.95。因此,对于信号检测可综合利用归一化残差与归一化余差的数值关系来实现信号检测。 4.2判决阈值对改进算法检测性能的影响分析 参数方面,观测点数为M=N/4,采用SNR= 10 dB、SNR=5 dB、SNR=0 dB和SNR=-5 dB 4种典型信噪比。采用文献[8]提供的归一化残差最优阈值η=0.9,进一步分析图2和图3中目标信号存在时首次归一化余差的变量区间与首次归一化残差和归一化余差之和的变量区间可知,归一化余差的阈值区间可选为[0:0.001:0.04],归一化残差和归一化余差之和的阈值区间可选为[0.6:0.01:1],统计得到检测概率与判决阈值的变化曲线如图4所示。通过分析图4可知: (1)在SNR=10 dB时,首次归一化余差的有效阈值区间为[0,0.028],首次归一化残差和归一化余差之和的有效阈值区间为[0.6,1]; (2)在SNR=5 dB时,归一化余差的有效阈值区间为[0,0.026],归一化残差和归一化余差之和的有效阈值区间为[0.6,1]; (3)在SNR=0 dB时,归一化余差的有效阈值区间为[0,0.026],归一化残差和归一化余差之和的有效阈值区间为[0.84,0.96]; (4)在SNR=-5 dB时,归一化余差的有效阈值区间为[0,0.02],归一化残差和归一化余差之和的有效阈值区间为[0.91,0.94]。 可见,改进算法的有效阈值区间随着信噪比的降低而减小。 图4 典型SNR下改进算法检测性能与阈值变化的关系Fig.4 The relation between detection performance of improved algorithm and threshold in typical SNR 4.3观测点数对3种算法的性能影响分析 参数方面,信噪比SNR=0 dB,观测点数M遍历范围为[0:2:40]。仿真分析改进算法与文献[7-8]所选算法的性能,最优判决阈值基于Monte Carlo方法选取,统计得到3种算法在不同观测点数下的检测性能情况如图5所示。 图5 不同观测点数下3种算法性能Fig.5 The performance of three algorithms in different observation points 由图5可知,在最优阈值下,与另外两种检测算法相比,改进的归一化残差算法用较少的采样点数便可实现较高的检测概率,有效减少了系统的采样成本。此外,3种检测算法在有效阈值下获得满足检测概率指标要求所需的最少采样点数,分别为30、30和24,进一步验证了改进算法相比于另外两种算法性能上的优越性。 4.4信噪比变化对3种算法的性能影响分析 参数方面,观测点数为M=N/4,信噪比遍历范围为[-15:1:15]dB。仿真分析改进算法与文献[7 -8]所选算法的性能,最优判决阈值基于Monte Carlo方法选取,统计得到3种算法在不同信噪比下的检测性能情况如图6所示。 图6 不同信噪比下3种算法性能Fig.6 The performance of three algorithms in different SNR 由图6可知:改进的归一化残差算法的检测性能明显优于另外两种算法;当信噪比较高时,3种算法的检测性能相似;在低信噪比下,如当信噪比为-8 dB时,3种算法的检测概率依次为0.807、0.934、0.984,只有改进算法能够满足指标要求,验证了该算法在低信噪比下的检测性能更好。 从运算量上来分析,OMP算法的运算复杂度主要体现在步骤2的最大投影系数搜索,运算复杂度的数学表示为O(MN),其中M和N分别代表压缩观测点数与冗余字典原子数目;文献[8]算法是基于OMP算法确定归一化残差,进而实现信号检测,运算复杂度的数学表示为O(MN);本文提出的改进算法是文献[8]算法的拓展,是基于两次迭代运算来进行检测判定,运算复杂度与其相当,因此改进算法的性能提高并没有引起复杂度的量级增加。 本文通过分析基于压缩感知的信号检测算法,针对OMP归一化残差算法没有充分利用残差能量信息的不足,提出了一种基于归一化残差和归一化余差相结合的信号检测算法。算法充分挖掘归一化残差特点,检测效果得到一定提高。仿真结果表明,算法可以在低信噪比(SNR≈-8 dB)和少采样点(M/N≈0.25)下高概率地检测目标信号。对于其他压缩感知信号,只要针对性的选择合适的稀疏基,本文算法仍具有适用性,这也是笔者下一步的研究方向。 [1] 蔡晶晶,宗汝,蔡辉.基于空域平滑稀疏重构的DOA估计算法[J].电子与信息学报,2016,38(1):168-173. CAI Jingjing,ZONG Ru,CAI Hui.DOA estimation via sparse representation of the smoothed array covariance matrix[J].Journal of Electronics&Information Technology,2016,38(1):168-173.(in Chinese) [2] 王良君,石光明,李甫,等.多稀疏空间下的压缩感知图像重构[J].西安电子科技大学学报,2013,40(3):73-80. WANG Liangjun,SHI Guangming,LI Fu,et al.Compressed sensing image reconstruction in multiple sparse spaces[J].Journal of Xidian University,2013,40(3):73 -80.(in Chinese) [3] PRIBIC R,KYRIAKIDES I.Bayesian compressive sensing in radar systems[C]//Proceedings of 2nd International Workshop on Compressed Sensing Applied to Radar. Bonn,Germany:IEEE,2013:1-5. [4] LANKA J,KIROLOS S,DUARTE M,et al.Theory and implementation of an analogy to information converter using random demodulation[C]//Proceedings of the IEEE International Symposium on Circuits and Systems. Piscataway,NJ,USA:IEEE,2007:1959-1962. [5] DAVENPORT M A,WAKN M B,BARANIUK R G.Detection and estimation with compressive measuranents[R].Houston,TX,USA:Rice ECE Department,2006. [6] DUARTE M F,DAVENPORT M A,WAKN M B,et al. Sparse signal detection from incoherent projection[C]// Proceedings of 2006 IEEE International Conference on A-coustics,Speech,and Signal Processing(ICASSP).Toulouse,France:IEEE,2006:305-308. [7] 刘冰,付平,孟升卫.基于正交匹配追踪的压缩感知信号检测算法[J].仪器仪表学报,2010,31(9):1959-1964. LIU Bing,FU Ping,MENG Shengwei.Compressive sensing signal detection algorithm based on orthogonal matching pursuit[J].Chinese Journal of Scientific Instrument,2010,31(9):1959-1964.(in Chinese) [8] 王康.基于压缩感知的LFM雷达信号侦查处理算法研究[D].北京:装备学院,2014. WANG Kang.Research on signal reconnaissance algorithms of LFM radar based on compressed sensing[D]. Beijing:The Academy of Equipment,2014.(in Chinese) [9] 张永顺,贾鑫,尹灿斌.基于压缩感知的直扩通信多音干扰抑制[J].电讯技术,2015,55(8):848-853. ZHANG Yongshun,JIA Xin,YIN Canbin.Direct sequence spread spectrum communications multi-tone jamming suppression based on compressive sensing[J].Telecommunication Engineering,2015,55(8):848-853.(in Chinese) [10] 黄凌.采用压缩感知的标准测控信号处理[J].电讯技术,2014,54(5):578-583. HUANG Ling.A TT&C signal processing method based on compressed sensing[J].Telecommunication Engineering,2014,54(5):578-583.(in Chinese) 秦国领(1990—),男,河南周口人,2014年于装备学院获硕士学位,现为工程师,主要研究方向为航天测控、信号处理和效能评估; QIN Guoling was born in Zhoukou,Henan Province,in 1990.He received the M.S.degree from The Academy of Equipment in 2014.He is now an engineer.His research concerns aerospace TT&C,signal processing,and effectiveness evaluation. Email:qinguoling@outlook.com 郑 森(1987—),男,山东德州人,助理工程师,主要研究方向为航天测控和现代信号处理; ZHENG Sen was born in Dezhou,Shandong Province,in 1987.He is now an assistant engineer.His research concerns aerospace TT&C and modern signal processing. 王 康(1989—),男,陕西渭南人,助理工程师,主要研究方向为信号处理和压缩感知; WANG Kang was born in Weinan,Shaanxi Province,in 1989.He is now an assistant engineer.His research concerns signal processing and compressed sensing. 李梓博(1991—),男,湖南郴州人,助理工程师,主要研究方向为信号处理和压缩感知; LI Zibo was born in Chenzhou,Hunan Province,in 1991. He is now an assistant engineer.His research concerns signal processing and compressed sensing. A Compressed Sensing Signal Detection Algorithm Based on Orthogonal Matching Pursuit QIN Guoling1,ZHENG Sen1,WANG Kang2,LI Zibo3 Considering that current signal detection based on compressed sensing does not effectively use amplitude information of sparse coefficient,this paper proposes a new method.Based on the orthogonal matching pursuit(OMP)algorithm,the concept of normalized residual is presented through analyzing transformation information of normalized residual.A two-dimensional(2D)signal detection algorithm is proposed in view of normalized residual and normalized remainder.Experiment results show that the effective threshold decreases continuously with the loss of signal-to-noise ratio(SNR),and the detection probability meets requirement under the condition of-8 dB SNR and 0.25 compression ratio.The algorithm possesses a good adaptability. compressed sensing;signal detection;orthogonal matching pursuit;characteristic quantity **通信作者:qinguoling@outlook.com :qinguoling@outlook.com TN914.4 A 1001-893X(2016)08-0856-06 10.3969/j.issn.1001-893x.2016.08.005 2016-01-22; 2016-05-11 date:2016-01-22;Revised date:2016-05-11 引用格式:秦国领,郑森,王康,等.一种基于正交匹配追踪的压缩感知信号检测算法[J].电讯技术,2016,56(8):856-861.[QIN Guoling,ZHENG Sen,WANG Kang,et al.A compressed sensing signal detection algorithm based on orthogonal matching pursuit[J].Telecommunication Engineering,2016,56(8):856-861.]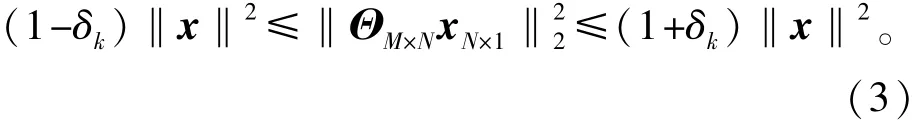


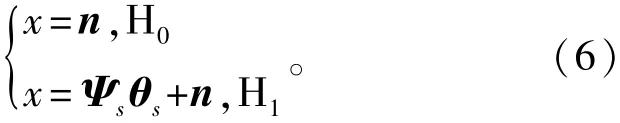

3 基于改进归一化残差的信号检测算法







4 实验结果及分析





5 结束语

(1.Jiuquan Satellite Launch Center,Jiuquan 732750,China;2.Xichang Satellite Launch Center,Xichang 615000,China;3.Unit 63778 of PLA,Jiamusi 154002,China)
