应用三维弹簧系统模型的锚节点部署优化*

毛玉明

应用三维弹簧系统模型的锚节点部署优化*

毛玉明**

（山东交通学院信息科学与电气工程学院，济南 264200）

为使随机部署的三维无线传感器网络中锚节点的分布更加合理，提高未知节点定位精度，针对锚节点部署进行优化。通过构建弹簧系统模型，将锚节点抽象为通过弹簧相连接的点，使部分锚节点在合力作用下进行伸缩运动，达到提高网络性能的目的。当锚节点部署优化完成后，应用近似三角形内点测试（APIT）和DV-HOP（Distance Vector-hop）算法测试优化前后的节点定位精度。仿真结果表明，三维空间下的锚节点经过弹簧系统模型的部署优化后，锚节点网络覆盖率和定位覆盖率均得到了提高，网络平均连通度有所提升，且定位精度显著提高。

无线传感器网络；弹簧系统模型；锚节点；部署优化

现有的无线传感器网络锚节点部署方式中大部分为自由部署，通过在监测区域随机抛撒来实现，随机抛撒的不确定性难以满足设计要求，为达到较高的定位精度和区域覆盖率，需要的锚节点数目较多且容易出现覆盖空洞、锚节点冗余和信道干涉等现象［3］；其次为确定性部署，通过制定部署方案，采用人工安置锚节点，这种方式虽然使整个网络成本最低，但在大规模节点部署中并不适用，适用范围有限［4］；最后为移动锚节点随机部署并优化，锚节点随机部署完成后，通过移动锚节点来小幅度地调整网络结构，降低了网络成本，提高了网络覆盖率和定位精度，但是由于移动锚节点的能量限制，锚节点的移动范围受限，因此需要通过部署优化算法来限定锚节点的移动路线［5-6］。

本文针对应用广泛的三维无线传感器网络，研究移动锚节点的部署优化机制，设计了一种三维弹簧系统模型针对随机部署的锚节点进行优化，使锚节点分布更加均匀，增加了网络覆盖率、锚节点定位覆盖率和网络的连通性。已有部分学者将弹簧系统模型应用于静态节点的定位中：朱慧勇［7］利用弹簧模型计算DV-HOP（Distance Vector-hop）算法中的平均跳距，相应提高了静态节点定位精度；陈万明［8］将节点虚拟为具有质量的粒子，粒子间互相使用弹簧相连，定位算法模拟外力将未知节点随机拉伸至某一位置，粒子在弹簧力作用下回到的位置即是定位位置。以上两种算法仅是通过模拟弹簧的伸缩运动来对未知节点定位，节点实际并未移动且所有节点均需参与运算，造成整体能耗过高。本文算法将弹簧系统模型应用于可移动锚节点的部署中，锚节点在弹簧力的作用下是真实运动的，且本文算法针对的是大规模随机部署的三维网络，仅移动部分锚节点，并应用现有定位算法即可取得较好的效果。

2　弹簧系统模型

首先做如下假设：

假设1 三维无线传感器网络中只有锚节点可以移动，未知节点并不移动，且锚节点的能量是有限的，随着能量耗尽，锚节点死亡。

假设2 锚节点与未知节点具有相同的通信半径r。

假设3 锚节点可在弹簧模型系统中抽象为一个点；而对于未知节点，为避免锚节点运动过程中与未知节点发生碰撞，将未知节点抽象为实心球形障碍物。

假设4 在通信半径r内的所有节点均可以直接相互通信，节点可以通过它们的ID来区分它们。

下面给出适用于三维无线传感器网络锚节点部署优化的弹簧系统模型。图1给出了弹簧系统模型N=（P，S）的原理示意图，其中P为锚节点集合，S为弹簧集合。图1中节点Pi∈P表示三维无线传感器网络中的一个可移动锚节点，弹簧Sij∈S连接网络中锚节点Pi和Pj，每一根弹簧都具有3个属性：弹性系数c、弹簧的初始长度l0和当前长度lij，锚节点Pi只与其三跳范围内的其余锚节点之间存在弹簧力。

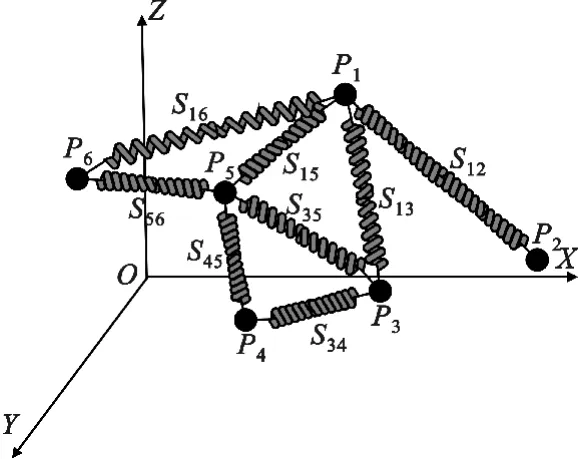
图1　弹簧模型原理示意图Fig.1　The theory of spring model

弹簧Sij的当前长度为锚节点Pi和Pj的欧氏距离。弹簧的弹力公式如下：

式中：Fi，j为弹簧Sij变形所产生的弹力；cij为弹性系数；lij为弹簧Sij的当前长度；l0为弹簧Sij的初始长度。

假设锚节点Pi、Pj的坐标分别是（xi，yi，zi）和（xj，yj，zj），则弹簧Sij的当前长度lij为

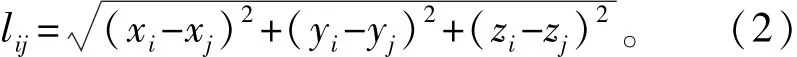
假设模型中存在3种初始长度的弹簧，即l1、l2和l3，其弹性系数c相同，但初始长度不同，其中：

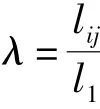
对于锚节点Pi，其所受的合力为

根据以上公式，可将三维传感器网络中的锚节点关系抽象如下：

（1）任一个锚节点Pi与其三跳范围内的其他锚节点间存在虚拟的弹簧力，该力既可能是引力，也可能是斥力，也有可能恰好为0，如图2所示；

（2）锚节点间通过互相通信，可获得相互间的欧氏距离，即弹簧Sij的当前长度lij，并根据选择系数λ设定弹簧Sij的初始长度；

（3）锚节点Pi所受合力为相邻三跳范围内的锚节点对其施加的引力和斥力的矢量和，如图2所示；

（4）锚节点Pi在受到合力的作用下做直线运动，经过移动后，若所受合力为0或小于阈值∂时，则停止移动；

（5）锚节点在运动过程中，根据其安装的旋转定向天线来判别运动路线中的未知节点，能自动绕过未知节点避免发生碰撞。

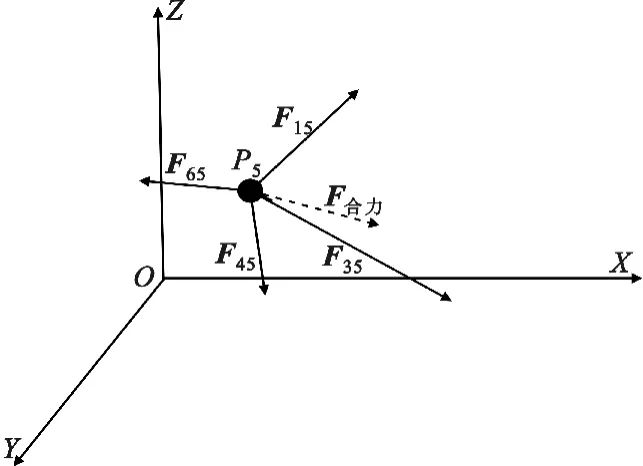
图2　锚节点受力示意图Fig.2　Force diagram of anchor nodes

3　基于弹簧系统模型的锚节点部署优化算法

在锚节点部署优化时，应尽量将在未知节点密度大的区域多布置锚节点，在未知节点密度小的区域少布置锚节点，这样可以减小定位误差，提高定位精度。因此锚节点首先通过与周围未知节点的通信来感知自身三跳范围内未知节点的数量，数量越多则证明锚节点周围未知节点密度越高，应使其余锚节点更靠近该区域。

根据锚节点三跳范围内未知节点的数量，选取前10%的锚节点做固定部署，这样既可使锚节点趋向于节点密度高的区域，又加快了锚节点部署优化的速度，是一种分布式的部署策略；其次锚节点在做若干次优化部署后，有可能能量即将耗尽，因此可设置能耗阈值，当节点能量小于时，也将此锚节点作固定部署，在弹簧系统模型中可假设做固定部署的锚节点被图钉固定到空间中，其余锚节点在弹簧力的作用下进行收缩扩展运动，如图3所示。

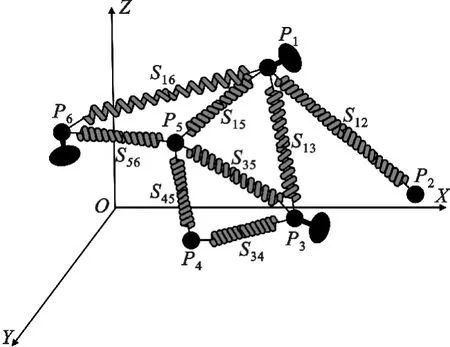
图3　锚节点部署优化示意图Fig.3　Optimal deployment of anchor nodes

基于弹簧系统模型的锚节点三维部署优化算法如下：

（1）锚节点与未知节点间相互通信，计算锚节点三跳范围内的未知节点数量；

（2）锚节点洪泛自身的信息，信息包括锚节点ID、三维坐标、剩余能量和周围未知节点数量；

（3）锚节点经过相互通信选取固定锚节点，并计算自身所受合力，获得将要到达的新坐标；

（4）锚节点按照直线进行移动，通过旋转天线规避路线上的未知节点；

（5）所有锚节点所受合力为0或小于某一极小值时，部署结束，否则重复步骤1～步骤4，直至所有锚节点都部署优化完毕；

（6）当锚节点死亡或有新锚节点加入时，重复步骤1～5直至重新部署优化结束。

锚节点部署优化算法流程如图4所示。

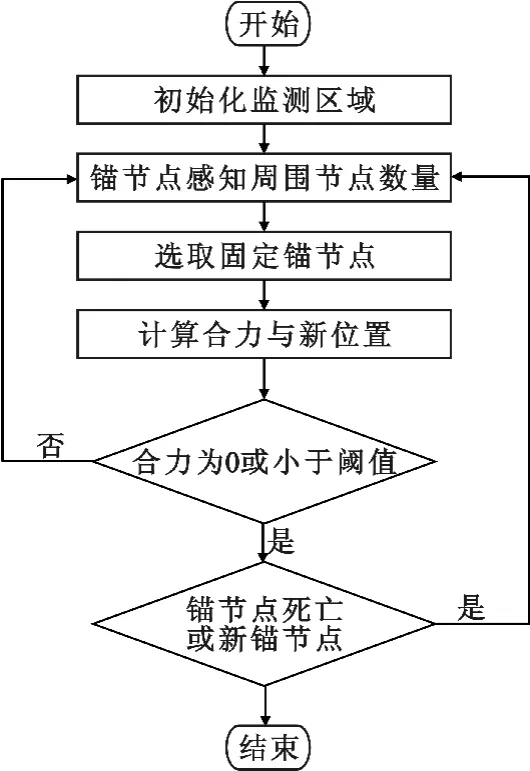
图4　锚节点部署优化算法流程图Fig.4　Flowchart of anchor nodes'optimal deployment

4　仿真分析

在现有的距离无关的定位算法中，APIT（Approximate Point-in-Triangulation Test）［9］和DVHOP［10］算法因定位精度较高、定位速度快和无需测距等特点，在实际工程中得到了广泛应用。本文针对锚节点部署优化前后的网络覆盖率、网络连通性进行了仿真比较，并使用APIT算法和DV-HOP算法从定位覆盖率和定位误差上进一步考察了锚节点部署优化后的网络性能；为便于仿真结果的描述，将锚节点部署优化后使用APIT和DV-HOP算法进行定位的过程称为APITANOD算法（APIT base on anchor nodes'optimal deployment）和DV-HOPANOD算法（DV-HOP base on anchor nodes'optimal deployment）。仿真环境设计为实验室理想环境下，节点随机分布于仿真空间中。为提高仿真精度、减少测试误差，考虑到上位机运算性能，所有仿真结果经过100次独立仿真求均值获得，实际应用中信号间的相互干扰有可能造成仿真结果的偏差，需进一步在实际环境中测试。仿真区域为300 m×300 m×300 m；未知节点数800；锚节点比例为5%，10%，15%，…，50%；通信半径r为30 m；弹性系数c为0.5；长度系数η为1。

4.1锚节点网络覆盖率

锚节点网络覆盖率即监测区域被锚节点覆盖的百分率，三维空间中将每个锚节点的传感范围视为一个以锚节点为球心的球体，然后使用若干个覆盖区域可重叠的球体覆盖三维监测区域的比例，即锚节点覆盖率。三维无线传感器网络中锚节点网络覆盖率可用以下公式计算：

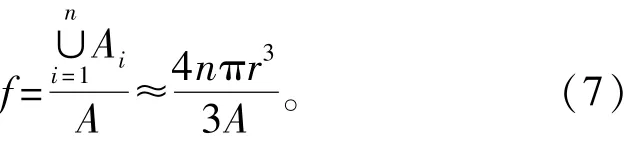
式中：Ai为锚节点i的球形覆盖区域；A为整个监测区域范围；r为锚节点的感知半径，假设锚节点感知半径与通信半径相同。锚节点部署的初始状态和经过部署优化后的网络覆盖率随锚节点比例变化曲线如图5所示。

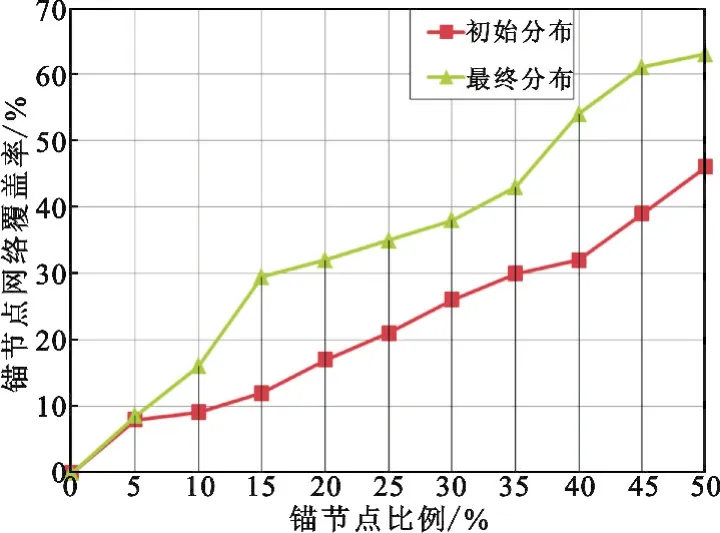
图5　锚节点网络覆盖率比较Fig.5　Comparison of anchor nodes'coverage

从图5中可以看出，随着锚节点比例的增加，部署优化前后的网络覆盖率都随之增加，但由于锚节点的随机部署造成了分布不均匀，增加了覆盖区域重叠的现象，因此部署优化后的网络覆盖率较优化前相比始终较高，体现了算法的优越性。

4.2网络连通性

无线传感器网络连通性保证了多跳自组织通信的开展，对通信、监测和定位等功能有着决定性作用。网络连通性是指网络中节点平均拥有的邻居节点数目，即网络平均连通度。假设网络中共有N个节点，节点i有Mi个邻居节点，则网络平均连通度公式如下：

在不同锚节点比例下，对锚节点部署优化前后的网络平均连通度进行了仿真实验，结果如图6所示。仿真结果显示随着锚节点比例的增加，锚节点部署优化前后的网络平均连通度均随之增加，但经过锚节点部署优化后，网络平均连通度在相同锚节点比例下有所提升。

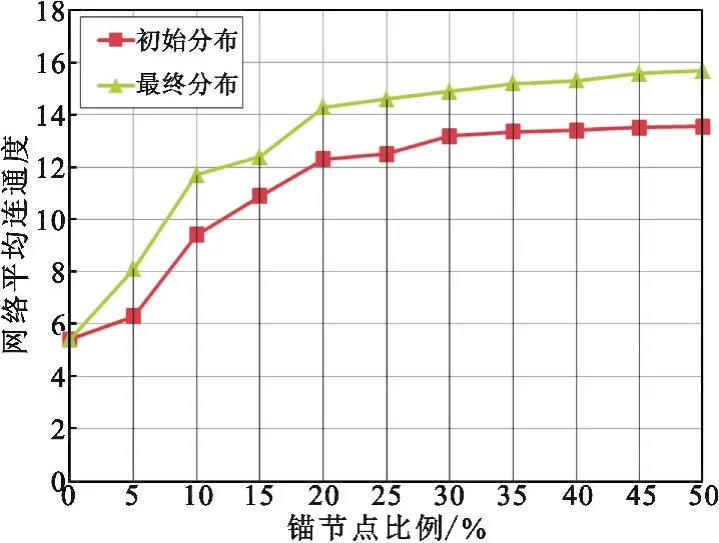
图6　网络平均连通度比较Fig.6　Comparison of connectivity

4.3定位覆盖率

定位覆盖率为已定位节点与未知节点总数的比值，其反映了定位算法对未知节点的定位成功率。在不同锚节点比例下，对DV-HOPANOD算法、APITANOD算法与锚节点优化前的DV-HOP算法、APIT算法分别进行了仿真比较，结果如图7所示。

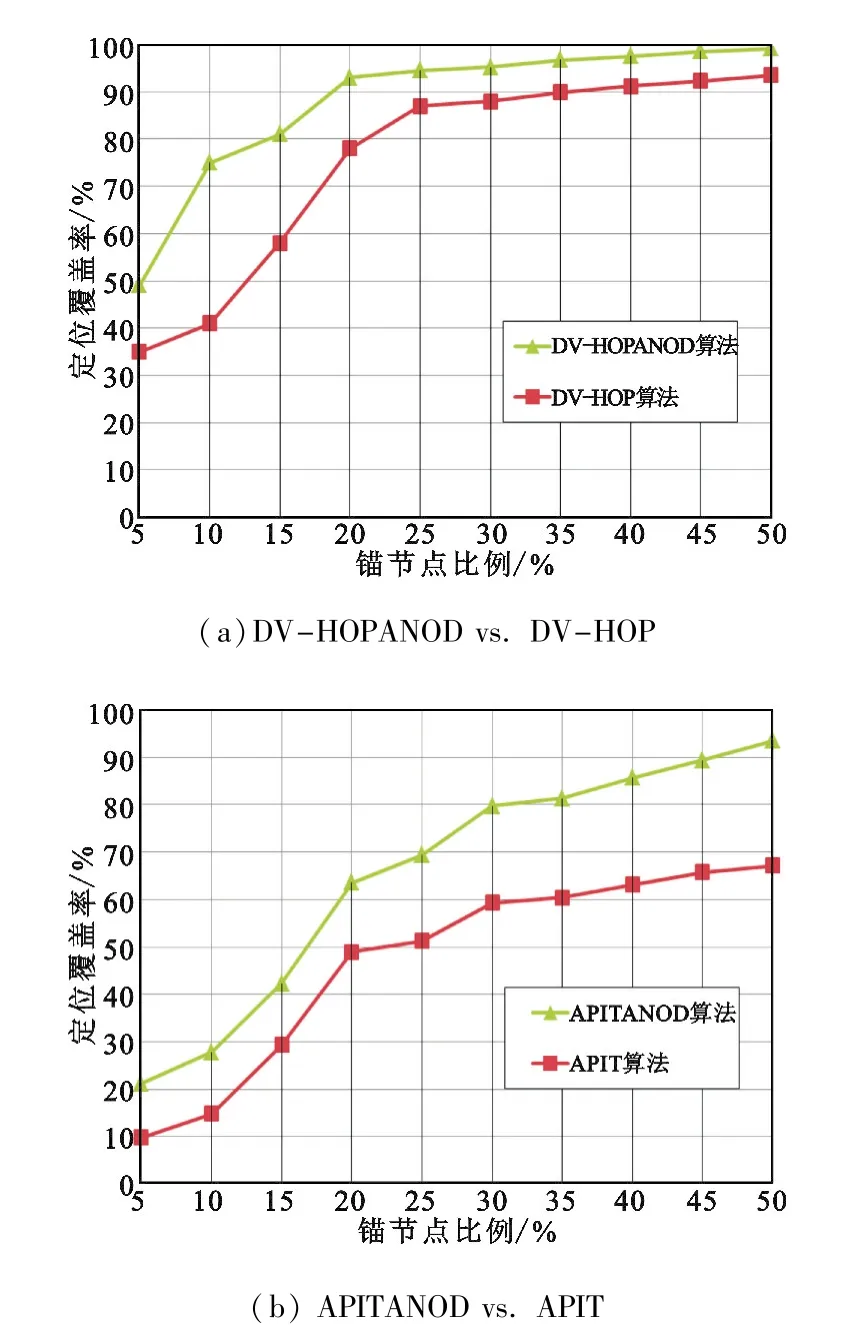
图7　定位覆盖率比较Fig.7　Comparison of localization coverage rates

从仿真结果可以看出，经过锚节点部署优化后，DV-HOPANOD算法和APITANOD算法都取得了较高的定位覆盖率，两种算法在锚节点比例大于30%时，定位覆盖率上升趋势变缓，说明锚节点超过一定比例后，锚节点数量的增加对定位覆盖率影响减小。

4.4定位误差

三维无线传感器网络中，节点的定位误差一般是指节点实际位置与估计位置之间的欧氏距离，为了从整体上考察定位算法的优劣，仿真方案采用未知节点的实际位置与估计位置之间的平均误差值与节点通信半径的比值来衡量定位的精度，即未知节点的平均定位误差。假设未知节点Ni的实际坐标为（xi，yi，zi），定位算法计算出的坐标为（x′i，y′i，z′i），设n为未知节点的数量，r为节点的通信半径，平均定位误差计算公式如下：

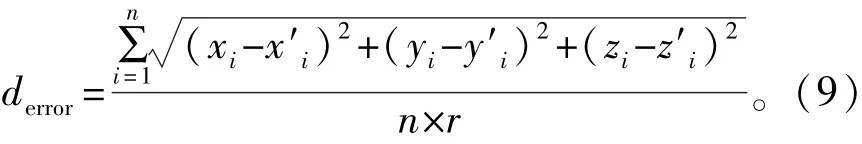
在不同锚节点比例下，对DV-HOPANOD算法、APITANOD算法、DV-HOP算法和APIT算法的平均定位误差做了仿真比较，结果如图8所示。

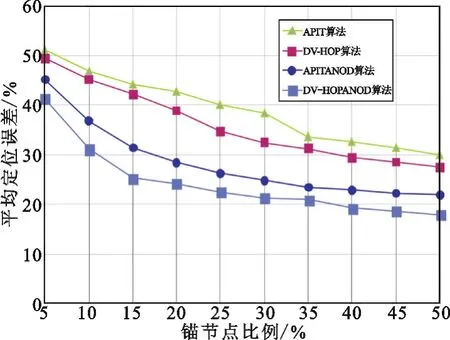
图8　定位误差比较Fig.8　Comparison of location errors

通过仿真结果可以发现，三维无线传感器网络随机部署后，由于锚节点分布的不均匀，特别是DV-HOP算法在根据锚节点间的相距跳数与距离来估算平均每跳距离时，造成了较大的误差，而APIT算法因锚节点的不均匀分布，造成了算法所需的四面体重叠区域少，对该算法的定位精度影响较大。经过锚节点的部署优化后，锚节点分布更加均匀，特别是兼顾了未知节点密度较大的局部区域，这些区域吸引了较多的锚节点，因此在相同锚节点比例下，DV-HOPANOD算法和APITANOD算法的定位误差明显小于其对应的未优化算法。实验数据也反应了锚节点比例的增加对平均定位误差影响较大，4种算法都随锚节点数量的增多，定位误差明显下降，特别是锚节点比例在5%～30%时，定位误差下降明显，超过30%后，定位误差下降趋势变缓。在实际应用时，可根据网络建设的成本来选择合理的锚节点比例，来达到定位精度与网络花销的平衡。

5　结束语

在三维无线传感器网络大规模应用中，在监测区域随机抛撒大量传感器节点后，极易造成锚节点的分布不均，严重影响了网络的性能。为解决这一问题，本文提出了基于三维弹簧系统模型的锚节点部署优化算法。以往研究仅通过模拟弹簧的伸缩运动来对未知节点定位，而本文算法通过对整个网络中的部分锚节点物理位置调整，大幅提高现有定位算法的定位精度，无需另外开发新的定位算法。仿真结果表明，该部署优化算法提高了锚节点的网络覆盖率、网络连通性和定位覆盖率，提高了三维环境下未知节点的定位精度，为无线传感器网络的大规模应用提供了一种实用的、经济性高的定位技术。因实际应用中电磁环境复杂，信号传输时极易造成干扰，为提高该算法的鲁棒性，应进一步通过实地测试来完善和改进算法。

［1］ 赵晓震，田庆战，孙牧.基于虚拟力驱动的传感器网络节点定位［J］.指挥控制与仿真，2012，34（6）：110-114.

ZHAO Xiaozhen，TIAN Qingzhan，SUN Mu.Location method for sensor networks nodes based on virtual force driving［J］.Command Control&Simulation，2012，34（6）：110-114.（in Chinese）

［2］ 刘海波，胡啸，贾浩.无线传感器网络节点自身定位算法综述［J］.电讯技术，2009，49（2）：80-86.

LIU Haibo，HU Xiao，JIA Hao.Review of node self-localization algorithms in wireless sensor networks［J］.Telecommunication Enginerring，2009，49（2）：80-86.（in Chinese）

［3］ 胡淼，陶正苏.一种基于可移动锚节点的DV-HOP改进定位算法［J］.电子设计工程，2011，19（24）：98-101.

HU Miao，TAO Zhengsu.A modified DV-HOP location algorithm based on mobile anchor node［J］.Electronic Design Engineering，2011，19（24）：98-101.（in Chinese）

［4］ STONE K，CAMP T.CAIRN：creating anchors for localization in realistic networks［C］//Proceedings of 2012 IEEE 31st International Conference on Performance Computing and Communications Coference.Austin，TX：IEEE，2012：225-235.

［5］ BROXTON M，LIFTON J，PARADISO J A.Localization on the pushpin computing sensor network using spectral graph drawing and mesh relaxation［J］.SIGMOBILE Mobile Computer&Communication Review，2006，10（1）：1-12.

［6］ 王文韬.应急救援场景下定位锚节点三维模型优化部署方法［J］.内蒙古师范大学学报，2014，43（2）：180-185.

WANG Wentao.Location nodes three-dimensional deployment in emergency salvage［J］.Journal of Inner Mongolia Normal University，2014，43（2）：180-185.（in Chinese）

［7］ 朱慧勇.基于弹簧模型的无线传感器网络定位研究［D］.广州：华南师范大学，2014.

ZHU Huiyong.The study of localization in wireless sensor networks based on a spring model［D］.Guangzhou：South China Normal University，2014.（in Chinese）

［8］ 陈万明.无线传感器网络基于弹簧模型的定位算法研究［D］.合肥：中国科技大学，2009.

CHEN Wanming.Localization in wireless sensor networks based on a spring model［D］.Hefei：University of Science and Technology of China，2009.（in Chinese）

［9］ 唐明虎，张长宏，昝风彪.无线传感器网络APIT定位算法［J］.微型机与应用，2010，29（21）：1-4.

TANG Minghu，ZHANG Changhong，ZAN Fengbiao.APIT localization algorithm in wireless sensor networks［J］.Microcomputer and its Applications，2010，29（21）：1-4.（in Chinese）

［10］ 张震，闫连山，刘江涛.基于DV-hop的无线传感器网络定位算法研究［J］.传感技术学报，2011，24（10）：1469-1472.

ZHANG Zhen，YAN Lianshan，LIU Jiangtao.Research of positioning technology in Wireless Sensor Network Based on DV-hop［J］.Chinese Journal of Sensors and Actuators，2011，24（10）：1469-1472.（in Chinese）

毛玉明（1980—），男，山东济南人，2014年获博士学位，现为讲师，主要研究方向为无线传感器网络技术。

MAO Yuming was born in Jinan，Shandong Province，in 1980.He received the Ph.D.degree in 2014.He is now a lecturer.His research concerns wireless sensor networks.

Email：18660106266@163.com

Optimal Deployment of Anchor Nodes Based on 3D Spring Model System

MAO Yuming
（School of Information Science and Electrical Engineering，Shandong Jiaotong University，Jinan 264200，China）

This paper proposes an optimal deployment algorithm of anchor nodes based on spring model system.The optimal deployment algorithm can improve location accuracy for randomly distributed three dimensional（3D）wireless sensor networks，and the anchor nodes'distribution is more reasonable.The algorithm abstracts the relationship of anchor nodes into dots and springs，and anchor nodes do concertina motion by the resultant force.Approximate point-in-triangulation test（APIT）algorithm and approximate point-intriangulation test（DV-HOP）algorithm are used to verify the optimized wireless sensor network.The simulation results show that the anchor nodes'network coverage and localization coverage are wider，and the connectivity of networks is better，and the positioning accuracy is higher.

wireless sensor network；spring model system；anchor node；optimal deployment

1　引 言

锚节点的部署优化是无线传感器网络研究热点之一，通过锚节点的部署优化，能有效利用有限网络资源，降低网络构建成本，提高网络覆盖范围及质量，延长网络的生存周期等［1］。目前，无线传感器网络锚节点的部署优化主要分为两个研究方向：一是为了使无线传感器网络更好地覆盖感知区域；二是为了使锚节点的分布更加合理，提高未知节点的定位精度［2］。目前大部分研究成果集中于提高网络覆盖率上，而很少利用锚节点的部署优化来提高定位精度。对于无线传感器网络定位研究来说，锚节点的部署和网络的拓扑结构是首先需要研究的问题，是定位算法的研究基础。

The Natural Science Foundation of Shandong Province（BS2015DX007）；The Open Research Fund from Shandong Provincial Key Laboratory of Computer Network（2015001）

**通信作者:18660106266@163.com 18660106266@163.com

TN929.5；TP212.9

A

1001-893X（2016）08-0850-06

10.3969/j.issn.1001-893x.2016.08.004

2016-03-30；

2016-06-27

date:2016-03-30；Revised date:2016-06-27

山东省自然科学基金资助项目（BS2015DX007）；山东省计算机网络重点实验室开放课题（2015001）

引用格式:毛玉明.应用三维弹簧系统模型的锚节点部署优化［J］.电讯技术，2016，56（8）：850-855.［MAO Yuming.Optimal deployment of anchor nodes based on 3D spring model system［J］.Telecommunication Engineering，2016，56（8）：850-855.］