基于内积运算和正交矩阵的并行扩频传输新方案*
2016-11-02龙德浩陈志清
龙德浩,陈志清
基于内积运算和正交矩阵的并行扩频传输新方案*
龙德浩**1,陈志清2
(1.四川大学,成都 610064;2.成都大学,成都 610106)
为了提高并行解扩的频谱效率和功率效率,提出了以内积运算为数学理论基础,以线性算子扩频、结合律并行扩频传输、分配律并行解扩为特征的IOR并行扩频传输方案,较经典并行扩频相关解扩和经典并行扩频匹配滤波解扩的频谱效率和功率效率分别提高了2 096 128倍和1 048 576倍。在8×randn(1,length(b))干扰下,并行扩频传输64比特,其100 000次大样本检验结果表明统计平均误码率和标准差分别为0.000 0和0.000 7。
移动通信;并行扩频传输;分组扩频传输;内积运算;正交矩阵;频谱效率;功率效率
2 IOR方案并行扩频与解扩方法
2.1理论根据
2.1.1Welch表达式
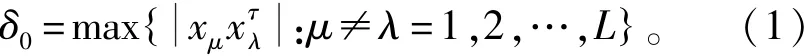
式中:xμ、xλ分别是矩阵c=(xij)M×L(i=1,2,…,M;j=1,2,…,L)的行μ与行λ的乘积。实质上,也是矢量代数定义下的“内积”。因此,如果c是任何“±1”正交矩阵(下同)⇆δ0=0,自同行pa=1,且定理1成立。
定理1 (1)任何正交矩阵的不同两行的内积皆等于零,(自)相同两行的内积均等于1;
(2)(异地而存的)任何两个相同正交矩阵的不同两行的内积皆等于零,相同两行的内积均等于1。
这两个结论本质上是用内积(数学)语言描述正交矩阵的物理结构特征,以便相关学科引用,并参与有关的数学运算,为内积运算与“±1”正交矩阵的工程应用奠定了数学基础。至于定理1的第2条,显然特别适合异地(例如收/发两端)而用的并行扩频传输±1比特的有关课题。
2.1.2与本文有关的内积运算的基本定律
交换律: 结合律与分配律: 式中:a、b和c都是元素为±1的同长度的矢量;r是实数,标量。 2.1.3关于内积与正交矩阵的重要推论 定理2 假设a(1:m,:)是元素为“±1”的正交矩阵,且m为大于等于32的正整数; 式中:a(i)为a(i,:),i=1,2,3,…,m;b是由正交矩阵a按其行、线性迭加而成的总矢量。则 (1)证明1(直观法) 再根据定理1,相同两行的共计m次内积运算皆等于1,故定理2即式(3)成立。 尽管上述证明定理2的方法直观明了,取舍有据,但书写复杂。为此,给出如下较为简约且较为严谨的数学证明方法。 (2)证明2(简约法) 由定理1和内积运算的结合律与分配律得知 式中:i,j=1,2,3,…,m。 因此,定理2或式(3)成立。即任何“±1”正交矩阵的任何行a(i,:)与其行线性迭加而成的总矢量b的内积 2.2新并行扩频传输与解扩方法 依照定理2,本文所提出的IOR并行扩频传输方案如图1所示,是由收发两端扩频/解扩的数据流矢量e/s、收发两端相同的正交扩频码/正交解扩码阵列p/p0、收发两端扩频/解扩和收发两端发送/接收矢量b/b1(Matlab表示)等8个模块组成的。其工作过程是:在发送端,首先,将待并行扩频传输的数据流矢量e和正交扩频码阵列p的各个分量e(i)和p(i)(i=1,2,3,…,m)按其行同时分别作用于扩频模块的两个输入端,其输出为已扩频数据矢量矩阵a的各个行分量a(i)(i=1,2,3,…,m);然后,将各个行分量a(i)(i=1,2,3,…,m)同时送入线性迭加模块以产生并行发送矢量b;至于高频部分不属基带讨论的内容,故不赘述。因此,在接收端,将接收到的、被噪声n干扰了的、线性迭加矢量b1=b+n与正交解扩码阵列p0的各个分量p0(i)(i=1,2,3,…,m)按其行同时分别作用于解扩模块的两个输入端,其输出为r(1),r(2),…,r(m),再同时极性判决,即形成已解扩的数据流矢量s。当干扰较弱时,已解扩数据流矢量s与扩频数据流矢量e是相同的;否则,不尽相同。下面将进一步阐述各个模块的形成与功能,并进行计算机仿真。 图1 IOR基带并行扩频与并行解扩原理图Fig.1 Schematics of IOR baseband parallel spreading and parallel despreading 2.2.1并行扩频传输的±1数据流矢量 在本示例中,并行扩频传输的±1比特数据流矢量 (m为大于等于32的正整数)是由1 024×1 024阶的小m矩阵s1024的第1 000行的1~m列的数据组成的,当m=1 024时,即可仿真并行扩频传输1 024比特的±1。其位置详见图1的扩频端的待发数据矢量模块e=(e(1),e(2),e(3),…,e(m))。 2.2.2扩频/解扩的正交阵列 在本仿真示例中,用于扩频的正交码阵列 是由正交矩阵c1的前m行组成的,而c1是由“±1”正交矩阵,例如行/列数都大于m的Walsh正交阵列产生的;用于解扩的正交码阵列是 由此可见,在本系统中,用于扩频的正交码阵列p与解扩的正交码阵列p0是完全相同的,其位置详见图1的并行扩频端-并行解扩端的“扩频/解扩正交码阵列模块p/p0”。 2.2.3扩频与b矢量 (1)扩频的方法(即线性算子) 其特点是,被传数据流矢量e的第i分量e(i)与扩频码矩阵p的第i行矢量p(i,:)同时作用于扩频模块的两输入端以实现“数乘”,其积就是已扩频数据阵列a(1:m,:),记为a;而a(i,:)(i=1,2,…,m)是已扩频数据阵列a的第i行已扩频数据矢量,其位置详见图1的扩频端的扩频码模块及其a(i,:)(i=1,2,…,m)都是严格有序的、待传输的、已扩频数据阵列a的各个分量。 (2)发送矢量b 为了克服现行分组和并行扩频传输的计算量较大、同步较麻烦等老问题,现依照内积运算的结合律定义 为已扩频阵列a按其行a(i,:)(i=1,2,…,m)线性迭加而成的IOR方案并行扩频传输矢量b,详见图1并行扩频输出端的矢量b模块。显然,尽管式(8)与式(2)形式相似,但涵义不同。 2.2.4内积解扩及其信号处理方法 接收端,收到的基带矢量是 式中:n=sn1*randn(1,length(b))是与b同长度的干扰矢量:sn1和length(b))的作用是分别控制正态分布噪声randn(1,length(b))干扰的强度和长度。考虑到定理1第2条、定理2及其矢量代数定义下的内积算法的结合律、分配律及其线性算子,将已收到的b1=b+n与解扩端的正交阵列p0的各个子矢量p0(1),p0(2),…,p0(m)按其序号同时作用于各个并行解扩模块的两个输入端,如图1所示,内积并行解扩的演算过程及其结果是 式中:i、j=1,2,3,…,m;〈p0(i,:),p(i,:)〉*e(i)和〈p0(i,:),p(j,:)〉*e(j)(i≠j)都是线性算子,e(i)或e(j)都是实数,又因为 故由定理1第2条得知 式中:i=1,2,3,…,m。 由此可见,我们所期待的IOR扩频传输方案的解扩结果包含两个分量:一是有用分量e(i),i=1,2,…,m;二是干扰分量〈p0(i,:),n〉,i=1,2,…,m或〈p0(i,:),sn1*randn(1,length(b))〉,i=1,2,…,m。因此,各并行解扩模块按其序号同时输出数据r(1),r(2),…,r(m)的幅度都是随干扰分量的强度而随机起伏的,不满足后续信号处理的要求。鉴于此,每一个解扩模块的输出信号都必须经过“极性判决”处理,其输出数据s(1),s(2),s(3),…,s(m)形成并行解扩输出±1矢量(模块)s,如图1的输出端所示,既便于如下的大样本统计处理,在直观上又便于与并行扩频传输矢量e的各个分量逐一比较。 3.1说明 为了验证上述IOR方案的合理性,需按照上述内积并行扩频传输与内积并行解扩方法,借助于Matlab语言,编写了一个仿真文件,简介如下: 函数名:bxsfcs12(c,c1,bxm,sn1,L)。 参数说明: (1)c为并行扩频传输的±1数据流矢量,例如数字图像源,在本仿真测试中实际使用的是或s1024,或g1024,或vivs1024等±1阵列产生的数据流矢量; (2)c1为用于扩频和解扩的“±1”正交阵列,例如walsh1024m、walsh2048m、walsh4096等Walsh正交阵列; (3)bxm为并行扩频传输的数据矢量的长度,例如8、16、32、64、128、256、512、1 024等,单位为比特,当并行扩频传输例如1 024比特时,更能发挥内积并行解扩快速的特点; (4)sn1为控制正态分布噪声randn干扰的强度sn1×randn; (5)L:检验L≈100 000个样本,旨在确保本仿真文件给出的误码率在大数据统计检验的结果是可信的。 下面是调用上述函数 在100 000次检验下导出了64比特的小m序列s1024的仿真结果:一是关键图形如图2所示;二是100 000大样本矩阵IOR100000sn_pe中元素xi,j∈RR ,i∈[1,2];j∈100 000是行/列数。 3.2仿真结果的关键图形 图2给出了新传输方案的仿真结果。 图2 内积运算与正交矩阵融合而成的并行扩频传输新方案的仿真图形Fig.2 Simulation results of high speed spread spectrum transmission scheme based on inner product operation and orthogonal matrix 3.3100 000样本的统计分析 (1)大样本数据的容量是size(IOR100000sn_ pe)=2×100 000阶矩阵; (2)大样本[g31]=Lsjyfb_tyff31(IOR100000sn_ pe(1,1:100 000),0.340 0)的统计平均信噪比及其标准差与样本平均信噪比及其标准差是相同的且分别等于-0.030 2 dB和0.096 5 dB; (3)大样本[g31]=Lsjyfb_tyff31(IOR100000sn_ pe(2,1:100 000),0.340 0)的统计平均误码率及其标准差与样本平均误码率及其样本标准差是相同的,且分别等于0.000 0和0.000 7; (4)显然,统计平均信噪比的标准差0.096 5越小,统计平均信噪比-0.030 2 dB越平稳;统计平均误码率的标准差0.000 7越小,统计平均误码率0.000 0越平稳;反之亦然。 4.1关于同步问题 因为IOR扩频传输系统收/发两端的解扩码阵列与扩频码阵列是相同的,即p0(1:m,:)=p(1:m,:),故由式(10)得知,依照内积运算进行并行解扩时,其中的参数是必然同时出现的。事实上,由图1可知,只要工作于IOR并行扩频传输状态,解扩码阵列p0(1:m,:)是自始至终存在着的。因此,只要串行接收解调成功,则内积〈p0(i,:),b1〉运算中的参数p0(i,:)和b1(i)=b(i)+n(i)(i=1,2,…,m)就必然同时出现于各解扩模块的输入端,且同时输出并行解扩的结果r(i)=e(i)+〈p0(i),n〉(i=1,2,…,m)。由此可见,对于IOR方案而言,收/发两端预置相同的扩频模块和解扩模块,本质上也是一种适用于内积分配律并行解扩的同步方式。 4.2关于扩频传输系统的频谱利用率与功率利用率 事实上,扩频传输系统的频谱/功率效率都与解扩的方法有关,而新型扩频传输系统的解扩方法与经典扩频传输系统的解扩方法是迥然不同的。因此,迄今为止,尚未出现适用于各种解扩方法的扩频传输系统的频谱/功率效率的计算方法或公式。鉴于此,本文依照相关检测三要素[1-2],以内积解扩为相关解扩的基本计量单位,从而把现存的3种不同解扩方法的计量单位在“内积解扩”意义下统一起来了。由此,导出了现存的3种扩频传输系统的频谱/功率效率的计算方法或公式及其示例如表1所示。 表1 并行扩频传输系统发展的历程Tab.1 Development progress of parallel spread spectrum transmission 由表1可知:近年来,由于引入了内积运算,码分多址通信理论变化显著,即由经典相关并行扩频传输→d相关并行扩频传输→IOR并行扩频传输,且立论依据和传输方案都不尽相同[1,3-5];至于解扩方法与计算量则完全不同。 当L=1 024时,IOR并行解扩较经典相关并行同步解扩、经典匹配滤波并行同步解扩,较d相关并行同步解扩、d匹配滤波并行同步解扩的频谱效率、功率效率都分别提高了L×(2L-1)=2 096 128倍、L ×L=1 048 576倍和L=1 024倍、L=1 024倍。由此可见,就并行解扩而言,显然,本文提出的IOR并行扩频传输方案是一种简约而有效的信号处理方法,较4G经典相关并行解扩的频谱效率和功率效率都远大于10倍。 本文根据定理1和定理2导出了IOR型扩频传输方案,并进行了详细推导和分析。 在民用无线多址信道上,如何使接收到的有用矢量b1与发送矢量b的误差(b1-b)较小呢?显然,这是IOR方案高频处理的关键技术之一,它涉及到天线、调制与解调及其快速锁相环等关键部件。如果在实地测试条件下其误码率亦能达到本文仿真的要求,那么,由4.2节及表1得知,IOR方案较第一节点方案、第二节点方案的并行解扩的频谱效率和功率效率都分别提高了百万倍和上千倍,且只需一个载波,因而结构简洁,可供5G参考。当然,本方案亦满足某些实用场合(例如远程精密外科手术)对实时图像传输的要求。 [1] 龙德浩,陈志清.δ/θ型基带相关检测/解扩方案[J].电讯技术,2012,52(9):1438-1442. LONG Dehao,CHEN Zhiqing.δ/θ base band correlation detection/dispreading scheme[J].Telecommunication Engineering,2012,52(9):1438-1442.(in Chinese) [2] WELCH L R.Lower bounds on the maximum cross correlation of signals[J].IEEE Transactions on Information Theory,1974,20(3):397-399. [3] 龙德浩,陈志清.基于δ匹配滤波器的扩频码同步门限检测方案[J].电讯技术,2014,54(3):265-275. LONG Dehao,CHEN Zhiqing.Spreading code synchronization threshold detection scheme based on δ-matched filter[J].Telecommunication Engineering,2014,54(3):265-272.(in Chinese) [4] 龙德浩,陈志清.适用于δ-相关解扩的扩频码检验方法[J].电讯技术,2012,52(10):1630-1634. LONG Dehao,CHEN Zhiqing.Spreading code test for δ/θ correlation despreading[J].Telecommucation Engineering,2012,52(10):1630-1634.(in Chinese) [5] 龙德浩,陈志清.δ/θ型相关解扩抑制多址干扰的能力分析[J].电讯技术,2013,53(5):551-559. LONG Dehao,CHEN Zhiqing.Analysis of δ/θ correlation despreadings ability to suppress multiple-access interference[J].Telecommunication Engineering,2013,53(5):553-559.(in Chinese) 龙德浩(1938—),男,四川乐至人,1961年于四川大学无线电系获学士学位,现为四川大学退休教授,主要研究方向为信息基础理论; LONG Dehao was born in Lezhi,Sichuan Province,in 1938.He received the B.S.degree from Sichuan University in 1961.He is now a retired professor.His research concerns information basic theory. Email:dehao1233@qq.com 陈志清(1943—),女,四川犍为人,1965年于四川大学数学系获学士学位,现为成都大学退休教授,主要研究方向为应用数学。 CHEN Zhiqing was born in Qianwei,Sichuan Province,in 1943.She received the B.S.degree from Sichuan University in 1965.She is now a retired professor.Her research direction is applied mathematics. A Novel Parallel Spread Spectrum Transmission Scheme Based on Inner Product Operation and Orthogonal Matrix LONG Dehao1,CHEN Zhiqing2 To improve the parallel despreading spectral efficiency and power efficiency,a parallel spread spectrum transmission scheme is proposed which is based on inner product operation and characterized by linear operator spreading,associative parallel spread spectrum transmission and the distributive parallel despreading.Compared with classical parallel spreading and relevant despreading scheme and classical parallel spreading matched filtering despreading scheme,the proposed scheme improves the spectral efficiency and power efficiency by 2 096 128 times and 1 048 576 times,respectively.In the condition of 8×randn(1,length(b))interference and 64 bit parallel spread spectrum transmission,100 000 large sample test results show the statistical average error rate and the standard deviation are 0.000 0 and 0.000 7,respectively. mobile communications;parallel spread spectrum transmission;packet spread spectrum transmission;inner product operation;orthogonal matrix;spectral efficiency;power efficiency 在图像等高速信息传输模式下,尽管M元扩频+δ相关解扩[1]和M元扩频+经典相关解扩(M=2k,k为大于等于8的整数)都能实现一次传输k比特信息码,但是,当k≈64/128时,其内积计算量较比特扩频的分别增大为M=264和M=2128。如此庞大的内积运算量,必然导致内积运算的总功耗增大,扩频传输的总速率降低,从而严重地制约了经典M元扩频传输系统的应用,而经典M元并行扩频传输系统也存在类似问题。鉴于此,本文基于“±1”正交阵列和矢量代数定义下的内积运算的交换律、结合律、分配律及其线性算子而提出了一个内积运算和正交矩阵融合而成的并行扩频传输新方案,简记为IOR方案。 **通信作者:dehao1233@qq.com dehao1233@qq.com TN911 A 1001-893X(2016)08-0862-05 10.3969/j.issn.1001-893x.2016.08.006 2015-11-11; 2016-04-05 date:2015-11-11;Revised date:2016-04-05 引用格式:龙德浩,陈志清.基于内积运算和正交矩阵的并行扩频传输新方案[J].电讯技术,2016,56(8):862-866.[LONG Dehao,CHEN Zhiqing.A novel parallel spread spectrum transmission scheme based on inner product operation and orthogonal matrix[J].Telecommunication Engineering,2016,56(8):862-866.]
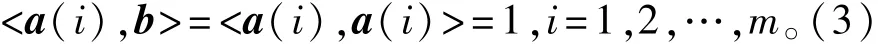



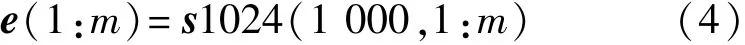
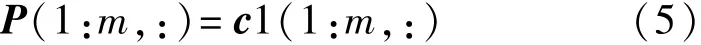
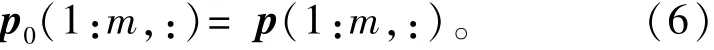

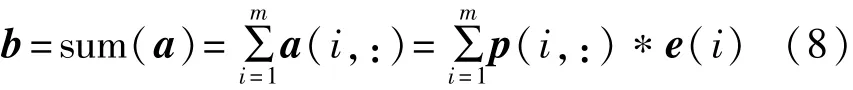
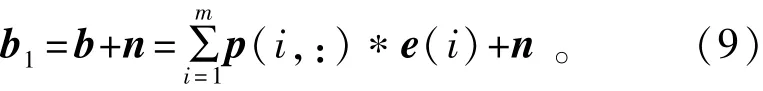


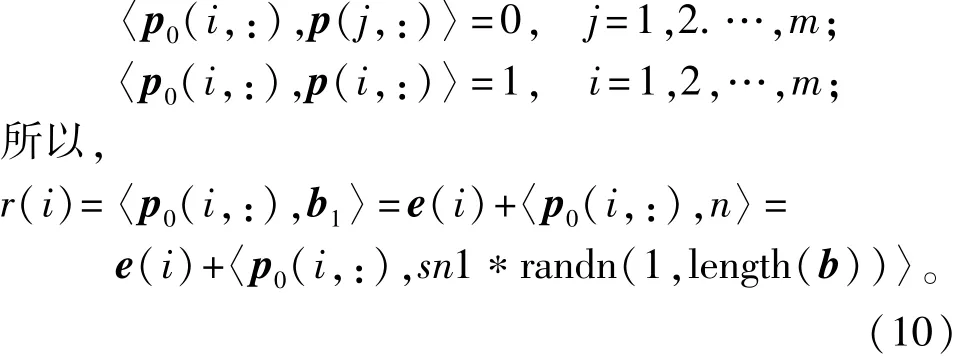
3 大样本仿真
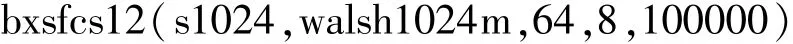

4 IOR扩频传输的同步、频谱效率与功率效率

5 结束语

(1.Sichuan University,Chengdu 610064,China;2.Chengdu University,Chengdu 610106,China)1 引 言
