面向兵棋推演的HPF行为动力学模型仿真实现与模型改进

张宇 柳少军 刘洋

1.国防大学信息作战与指挥训练教研部北京100091

基于对人类行为实证数据的分析,运用数学、系统科学、统计学和非线性科学等理论,研究纷繁复杂的人类行为的特征、规律与动力机制,是行为动力学中一个重要的研究内容,对于研究经济、政治、军事等众多社会学类学科具有重要意义.近年来,随着计算机仿真技术的不断发展,目前我军大型兵棋系统已基本实现了对战争全要素、全过程的模拟仿真,兵棋推演已经逐渐成为我军模拟训练和研究作战问题的重要手段,利用兵棋推演锻炼指挥员战役级作战行动的指挥能力也成为目前我国兵棋系统应用的一大亮点.推演过程中系统实时记录了大量真实的指挥行为实证数据,为面向兵棋推演的行为动力学研究提供了坚实的数据支撑.指挥行为动力学研究不仅有助于对指挥员的推演过程进行科学合理的分析,而且可以针对指挥员推演行为的模拟仿真和未来兵棋系统智能功能的开发打下基础.

进入21世纪后,针对行为动力学问题的研究已经引起了有关学者的重视,并在理论层面获得了较大的突破.奥地利经济学家路德维希·冯·米塞斯在尝试探索经济学根基的过程中,最早提出了以逻辑架构为研究内容的人类行为研究方法.按照传统近似的方法,一般将人的行为规律描述为近似泊松分布的稳态随机过程.其主要特征体现在相继行为之间的时间间隔方差较小,且行为的偶发状态较少且可近似忽略.

但是,2005年,Bar˙abasi[1−2]通过统计用户发送和回复邮件行为的时间间隔,发现时间间隔同时具有长时静默与短时高爆发的特征,相邻事件中的时间间隔分布呈现出近似反比幂函数的重尾特性,这种时间标度的特征是在对人类商业活动、网络使用、管理活动、计算机指令使用等方面的时间间隔研究中得到进一步证实.大量实证统计说明人类行为可能存在满足其他特性的动力学机制.为解释此类特征的动力机制,Bar˙abasi[2]基于优先权决策理论构建了基于任务选择的最高优先权优先(Highest Priority First,HPF)排队模型.

1 HPF动力学模型描述

Bar˙abasi认为,人类行为时间上的阵发与重尾特征,是基于排队过程的决策结果造成的.据此,Bar˙abasi[2]构建了HPF动力学模型.模型的主要思想是,人通常将需要完成的任务组合成一个动态的任务列表,然后基于个体对不同行为轻重缓急的认知差异,为它们赋予不同的优先权系数.然后,个体按照行为优先权和一定的决策协议实施行为.基于优先权优先的人类动力学模型可以描述为:

1)对行动建立一个包含L项任务的列表,每项任务具体的优先权参数xi(xi=1,2···,L)由分布函数p(x)得到;

2)随着时间推进,每个离散时间会选择一个任务进行处理,个体以概率p执行优先权最高的任务,并以概率1−p执行一个完全随机的任务;

3)当一个任务完成后,会有下一个新任务对已执行任务进行替换,新任务的优先权仍由p(x)产生.

由该模型的定义[4]可知,当概率p→1时,优先权最高的任务会被执行,当概率p→0时,模型将对所有任务进行随机选择.在这种服务HPF规则下,被判定为优先权最高的任务,即使它最晚加入任务列表,仍然会被首选执行.这就能很好地模拟人类行为的一种规律,即人类在众多事务需要处理时,会优先地选择重要或者急切需要完成的事务;因此,该模型使得优先权较低的行为被新加入的优先权较高的行为插队,低优先权的任务却需要等待所有比其优先权高的任务都完成后才能被执行,因而低优先权的任务将被迫长时间停留在队列中,从而产生任务执行中等待时间出现“重尾”现象.

2 模型仿真实现

根据Bar˙abasi提出的模型概念,选取事件调度法,运用MATLAB对Bar˙abasi的HPF动力学模型进行仿真模拟.事件调度法能直接对事件进行调度,通过按照特定的时序对事件进行调度,从而实现对系统动态变化的模拟.这就要求模型在执行事件调度时,要对事件进行扫描、识别、执行等程序.同时,事件列表随着事件的选择执行不断进行“加入”、“删除”等更新.

HPF动力学模型在描述上近似于带权值的经典M/M/1模型,因此,在经典模型中加入优先权变量和模拟变量,使用MATLAB程序对模型进行程序设计,具体设计流程如图2.模型的仿真旨在通过计算机随机生成的模拟行为得到间隔时间的分布情况.

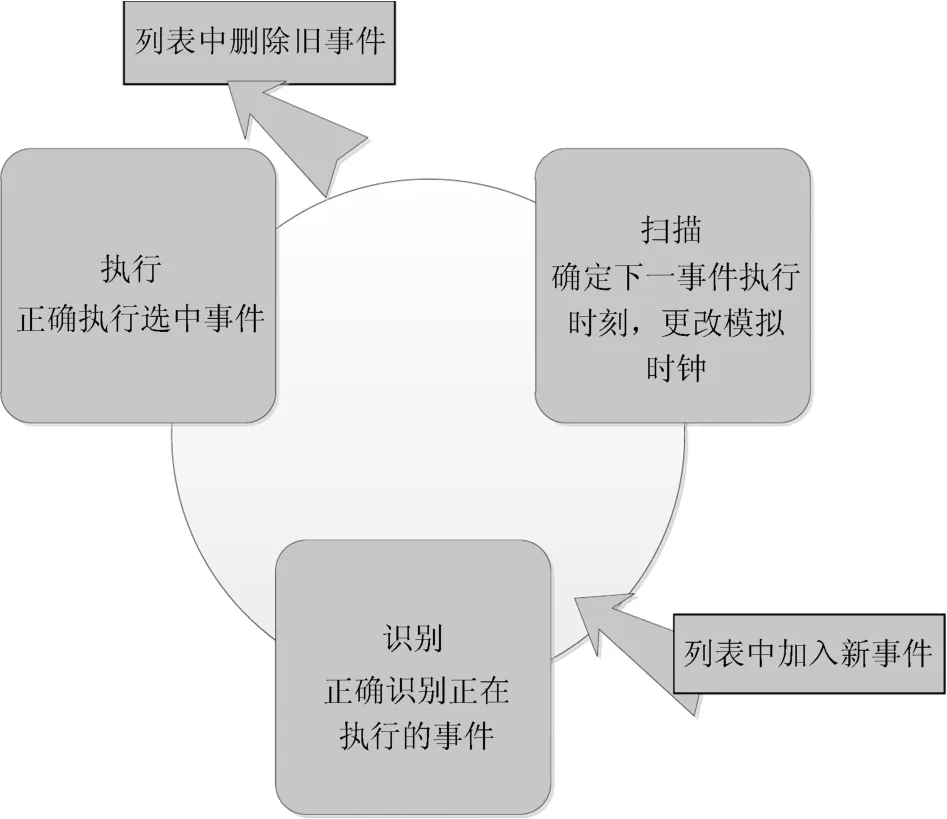
图1 时间调度法流程示意图

图2 HPF模型仿真流程图

为模拟行为选择执行情况,模型中将所执行的任务看作相互离散的时间模拟仿真.设计模拟变量:任务到达时刻ta;任务离开时刻tb;任务列表总长L;任务优先权参数θ;模拟时间tc;结束时间td;事件类型e;时间执行时刻te,等待时间tw等.

在设置服务台n=1、新任务到达率λ=0.8、系统服务率µ=0.5、1000次循环的情况下,仿真结果显示模型时间间隔t与间隔时间概率P(t)在双对数坐标系下的分布情况如图3.由仿真结果可知,该模型能较好地反映人类行为的幂律分布及“重尾”特征.经过多次模拟,该条件下幂指数约为1.58.

3 兵棋推演中指挥行为数据时间间隔实证分析

通过对兵棋指挥行为数据进行时间维的实证分析,从中也发现了类似的特征.时间间隔分析:兵棋推演指挥行为数据集中对时间维的记录单位为“分钟”,由于指令下达的时间一般以秒为单位,单位分钟的粒度较大,很难满足指令下达的时间间隔要求,所以对时间数据进行处理.按以下规则进行时间处理:

将处理好的单位为“秒”的数据进行对于相邻的同一指令的时间间隔分析,表1给出连续两个相同指令时间间隔部分统计结果.

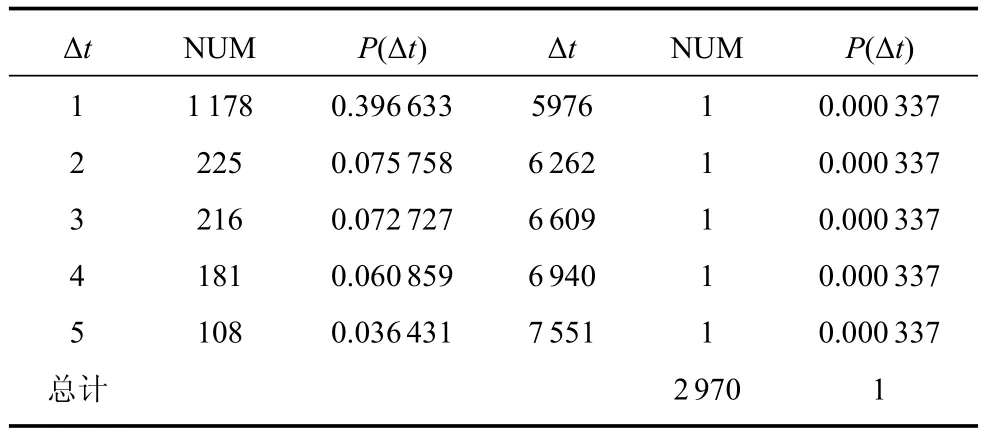
表1 一次推演过程中红方作战集团连续两个相同指令下达时间间隔Δt—P(Δt)部分分布表

图4是一次推演过程中红方作战集团指令下达时间间隔在双对数坐标系下的分布图,利用线性回归方法对该次演习的主体数据进行拟合得到图中直线,分析得到幂指数为1.65685,相关系数R=0.81232.而且,同一指令相邻两次的时间间隔最大值超过7000s,在时间间隔幂律分布图中明显呈现出“重尾”的特征.结果显示,红方作战集团在推演过程中综合各指令下达的时间间隔服从幂律分布.

可见,指挥员在兵棋推演过程中会在短时间内对某些指令进行快速频繁的下达,同时在一定时间内出现某些行为的“静默”,导致阵发和“重尾”现象同时发生.这说明指挥员在推演过程中对待各类指令的使用频率和处理方式都是不同的,各类指令类型存在优先权差异.

图3 用MATLAB仿真模型的时间间隔在对数坐标系下的概率分布

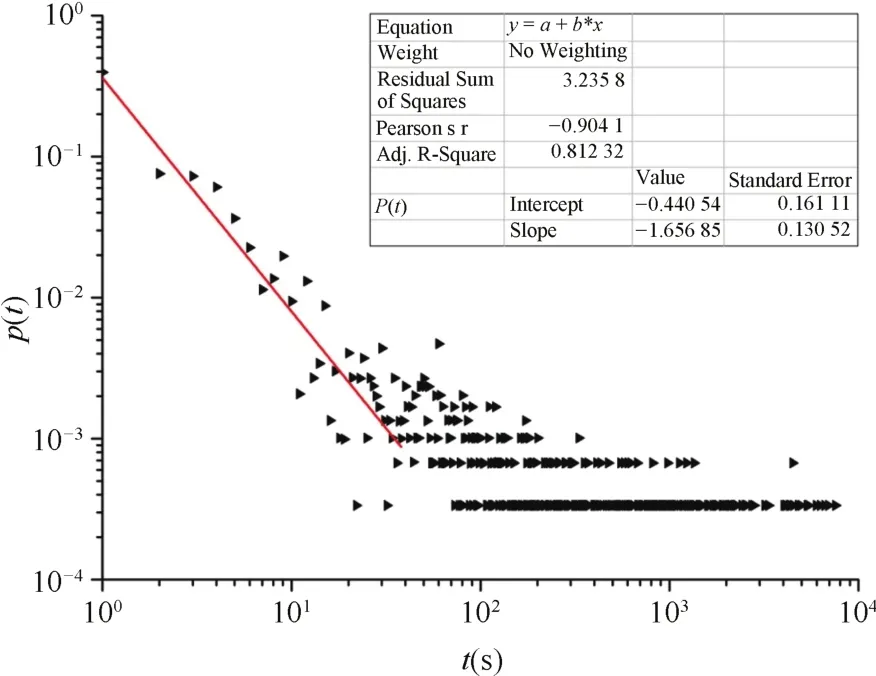
图4 一次推演过程中红方作战集团连续两个相同指令时间间隔在双对数坐标系下分布图

4 实证比对与模型改进

4.1 实证对比

对比图3和图4可以看出,模型的仿真结果与兵棋推演中实证数据的统计结果具有较大的相似度:

1)在双对数坐标系下,模型模拟结果与实证统计结果均呈现明显的幂率分布特征,幂指数分别为1.58、1.66;

2)两种结果在图中均反映出概率分布较小的大时间间隔出现,即明显的“重尾”特征.

基于HPF动力学模型描述兵棋推演中指挥行为的时序规律在这两方面具有较强的可用性.即可以用HPF模型对兵棋推演中指挥员下达指令的行为进行模拟和解释.在实际推演中,指挥员根据作战任务、作战目标、作战阶段的不同,也可以看作将准备实施的任务按照自我认知进行不同优先级的划分.这与Bar˙abasi提出的基于任务选择的HPF动力学模型相契合.

4.2 动力学分析模型的改进

Bar˙abasi基于任务的行为动力模型对于兵棋推演过程具有一定的科学性,通过相邻两条作战指令间隔时间的分析,得出兵棋推演中的指令下达行为近似满足幂指数为1.65685的幂律分布.相邻指令下达等待时间的差异间接反映了推演过程中指令的优先权的差异.基于事件优先权优先的动力模型解释兵棋推演指挥行为的阵发、幂律分布以及“重尾特征”是可行的.但是,Bar˙abasi的动力学模型与推演行为具有一定的局限性.主要表现在两个方面:

1)模型未考虑截止时间.由于Bar˙abasi模型优先权参数的设置是静态的,因而无法解释具有截止时间的行为.兵棋推演过程并不是无休止的,需要在某一规定时间内完成;

2)模型未考虑阶段特征.兵棋推演数据在时间上反映出明显的阶段特征;这就需要在基于任务的模型中加入其他影响因子,本文拟将对任务的兴趣引入行为动力模型的构建,即在模型中设计兴趣递减因子.当演习每一阶段开始时,设置兴趣因子随时间的变化函数,从而反映推演过程的阶段特征.

因此,提出一个具有服务截止时间并加入兴趣递减因子的行为动力学模型改进方案:假设事件列表的长度为L,服务时间序列服从参数θ(θ＞0)的负指数分布,且时间之间相对独立.在时间步长在执行一个行为Fi时,首先在区间(0,1)上抽取优先权参数x1,此类事件则以概率Π(xi)=xi接受服务[4].引入时间变量t,当t=0时,事件列表为静态L;当t＞0时,个体以概率p执行优先权最高的任务,并以概率1−p执行一个完全随机的任务[3].假设t=0事件数为L,则列表中事件的执行概率为

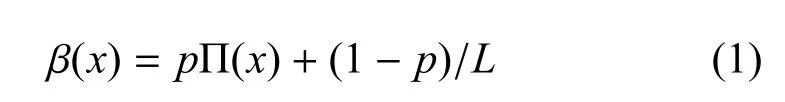
当由一个新的任务加入队列时,模型共执行了n−1个任务的概率为

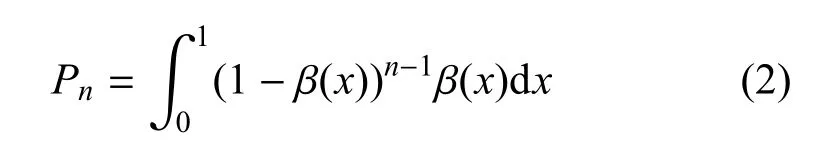
引入“兴趣——时间”函数来描述兴趣因子:兵棋推演的实际情况是在每个作战阶段的初始时间段参演人员对兵棋推演比较有兴趣,随着推演进程的逐步深入,参演人员对推演的兴趣会有一个变高至顶点再逐渐降低的过程.当截止时间t接近T-Δt时,兴趣因子会随着时间的迫近出现一定的上升.基于这种特征,可以设置兴趣因子与推演时间的函数δ(t)

3)当t时间步长,有新的任务加入时,执行该指令的概率为:

4)λ表示兴趣因子的影响系数.引入截止时间和兴趣因子后,模型将更加符合兵棋推演作战指挥行为的时序特征.

5 结论

本文基于人类行为动力学相关理论,使用MATLAB对HPF模型进行了仿真实现,面向兵棋推演,时间间隔幂律分布与“重尾”特征多角度对实证数据进行了时序分析.时序分析结果显示:一次兵棋推演过程中作战指挥行为近似满足幂律为1.65685的幂律分布.而后,根据兵棋推演的现实特点,引入“截止时间”和“兴趣因子”对Bar˙abasi基于任务驱动的行为动力模型进行了改进.本文将根据实证分析研究结果进一步改进模型,并在未来的工作中对模型进行仿真验证,增加模型的仿真度和可信度.