环上SS-元素的性质及其应用

李小光

(西安航空学院 党政办公室，陕西 西安 710077)



环上SS-元素的性质及其应用

李小光

(西安航空学院 党政办公室，陕西 西安 710077)

介绍环上的SS-元素，并研究环上SS-元素的特征。运用SS-元素研究群的代数类，得到环上SS-元素的一系列性质，并给出了一些相应地例题。

SS-元素；SS-环；群代数

0　引言

在文献[1]中，W.B.V.K.[1]首先提出了SS-元素的定义：若环中的元素满足a2=a+a，则这些元素被称为环的SS-元素。在具有单位元的环中，我们总可以找到2个SS-元素，一个是环的加法单位元0，另一个是环的平凡SS-元素2,(2=1+1)；环上除了加法单位元0和平凡SS-元素2之外的SS-元素称为非平凡SS-元素；至少包含一个非平凡SS-元素的环称为SS-环。SS-环中包含零因子和非零因子。文献[2]中证明了，若环中元素是非平凡SS-元素，则该元素一定满足a2≠a，因此，环的幂等元素不可能是非平凡SS-元素，布尔代数被称为环或布尔环，但一定不是SS-环。

1　一些实例

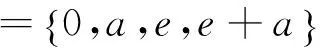
在该运算法则下是一个群代数。

表1　运算法则1

表2　运算法则2

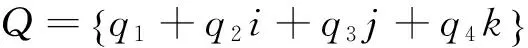
=q1q11+q1q21i+q1q31j+q1q41k+q2q11i+

q2q21i2+q1q31ij+q2q41ik+q3q11j+q3q21

ji+q3q31j2+q3q41jk+q4q11k+q4q21ki+

q4q31kj+q4q41k2

环Q中非平凡的SS-元素是1+i，1+j，1+k，i+j，i+k，j+k，1+i+j+k，因此Q也是SS-环。

2　SS-元素与非平凡SS-元素

定理1设R是环，a是R中的非零元，则a是SS-元素的充分且必要条件是

(1)a2≠a；

证明：充分性：假设a是环R的非平凡SS-元素，a2=a，a+a=a，

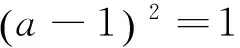
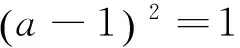
定理2设R是环，则下列的结论成立：

证明：显然，环R中“*”和“。”运算的单位元分别是1和0。

从而，我们可知，环R的非平凡SS-元素，当且仅当该元素存在其拟逆元。

=a2-a2ra-ara2+ara2ra

=a+a-ara-ara-ara-ara+ara+ara

=a+a-ara-ara

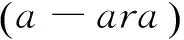
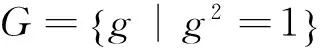
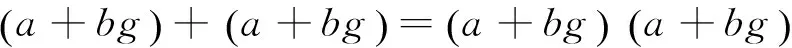
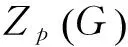
a+a=a2+b2，b+b=ab+ab，a=1

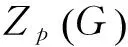
3　SS-元素的性质

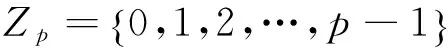
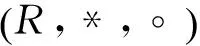
4　结论

综上，我们可以构造一个环上的SS-元素来计算零元素的非零因子的个数，并得到了其相关性质，今后将在本文的基础上继续研究SS-元素的商结构。

[1] Swamy W B V K.On SS-rings[J].Math.India,1998,60(1):13-23.

[2] Rao A K S C S.A Note on SS-rings[J].Math.India,2000,9(2):48-53.

[3] Lambek J.Lectures on Rings and Modules[M].India:Blasdellpublish,1966.

[4] Bakhshi M,Borzooei R A.Lattice Structures on Fuzzy Congruence Relations of A Hypergrouoid[J].Information Science,2007,177(16):3305-3313.

[5] Borzooei R A,Zahedi M M.Fuzzy Positive Implicative Hyper K-ideals[J].Pure and Appl.Math,2003,14(5):9-22.

[6] 吴忘名.Fuzzy蕴含代数[J].模糊系统与数学，1990,4(1)：56-63.

[7] 王国俊.非经典数理逻辑与近似推理[M].北京:科学出版社,2000.

[8] 谢云鹏.基于包含度的模糊不定性度量[D].西北大学,2008.

[9] 姚炳学.群和环上的模糊理论[M].北京:科学出版社,2007:84-88.

[责任编辑、校对：周千]

The Properties and Applications of SS-Elements in the Ring

LIXiao-guang

(Party and Government Office,Xi'an Aeronautical University,Xi'an 710077,China)

The definition of SS-elements of a ring is introduced,and its properties are studied.A class of group algebras is studied on the basis of SS-elements to produce a series of properties of SS-elements,and some corresponding examples are presented.

SS-elements;SS-ring;group algebra

2016-06-24

李小光(1973-)，女，辽宁铁岭人，副教授，从事代数学及信息论方面的研究。

O153.1

A

1008-9233(2016)05-0072-03