数字下变频系统实现研究

宋　飞

(西安航空学院 电子工程学院，陕西 西安 710077)



数字下变频系统实现研究

宋飞

(西安航空学院 电子工程学院，陕西 西安 710077)

在软件无线电架构背景下，研究了数字下变频中的数据抽取理论，提出了数字下变频处理系统方案，即4倍抽取采用多相结构来实现，抗混叠滤波采用FIR滤波器来实现。同时利用系统时间余量实现了多载波处理与多相处理的结合，既能够节约硬件资源又能够充分利用系统时间余量提高资源利用率。在FPGA中进行实现，能够达到满意的抽取和滤波效果。

数字下变频；整数倍抽取；多相结构 FIR滤波器；多载波叠加

0　引言

软件无线电是一种新型的无线体系结构，整个系统采用动态的软件编程对设备特性进行重配置，即硬件通过软件定义来完成不同的功能，从而建立一种多模式、多频段、多功能无线设备的有效且经济的解决方案。软件无线电的主要特点：可多频带、多模式、多功能(M3)工作；具有可重配置、可重编程的能力[1]。

软件无线电接收机主要由三大部分组成：模拟射频前端、高速模数/数模转换器、数字信号处理单元。其中宽带中频带通采样是近期软件无线电一种较可行的技术体制，通过增加一点射频前端的复杂性，使A/D设计大大简化，从而解决了在其他技术体制下A/D器件无法满足要求的情况[2]。

本文重点关注的是该技术体制下的数字下变频部分，其由NCO、数字混频器、低通滤波器、抽取器构成。NCO主要用于产生本振信号，与数字混频器一起使接收的数字中频信号下变频到零中频。低通滤波器用于数字抽取所必须的抗混叠滤波。抽取器则用于降低数据采样率，利于后续处理。这些模块实现较灵活，可采用多种目前主流应用的芯片来实现。

数字下变频子系统是软件无线电体系的核心所在，也是软件无线电接收机中的重点研究领域。

1　数据抽取理论

根据带通采样定理，软件无线电接收机的带通采样率应尽可能选的高些，这样可使瞬时采样带宽尽可能的宽些，从而对不同带宽的信号有更好的适应性，同时也有利于简化系统设计。但采样率提高会导致采样后的数据流速率很高，导致后续信号处理速度无法满足需要。因此，有必要对采样后的信号进行降速处理，这就是多速率信号处理技术中的数字下变频(DDC)理论。

整数倍抽取是指把原始采样序列x(n)每D个数据抽取一个，形成一个新的序列xD(m)，即xD(m)=x(mD)。若原始采样序列的采样率为fs，则其无模糊带宽为fs/2；D倍抽取后的新序列，其采样率变为fs/D，其无模糊带宽为fs/2D；则当x(n)含有大于fs/2D的频率分量时，xD(m)就必然产生频谱混叠，导致无法恢复出x(n)中小于fs/2D的频率分量[3]。

对于x(n)信号，定义一个D倍抽取后的新序列：

(1)

则可得抽取后的序列xD(m)的离散傅里叶变换为：

(2)

由此式可见抽取序列的频谱为抽取前序列频谱经频移和D倍展宽后的D个频谱的叠加和。

为了能够正确恢复出原始序列中所感兴趣的频谱分量，可以首先用一个数字滤波器(带宽为π/D)对X(ejw)先进行滤波，使其只含有小于π/D的频率分量，这样再进行D倍抽取就不会产生频谱混叠现象，从而可完全恢复出原始序列的信息。该低通滤波器被称之为抽取抗混叠滤波器。抽取抗混叠滤波器与采样率降低器合称抽取器。其结构如图1所示：

图1抽取器的结构

由图1可见，抽取器的抗混叠滤波器位于抽取算子D之前，即在降速之前实现，大大提高了对运算速度的要求，使用多相滤波结构可较好解决这个问题。

对其重新组织可写为：

(3)

(4)

此即为数字滤波器H(z)的多相表达式；又可利用抽取器的等效变换，得到抽取器多相结构的高效形式，如图2所示。

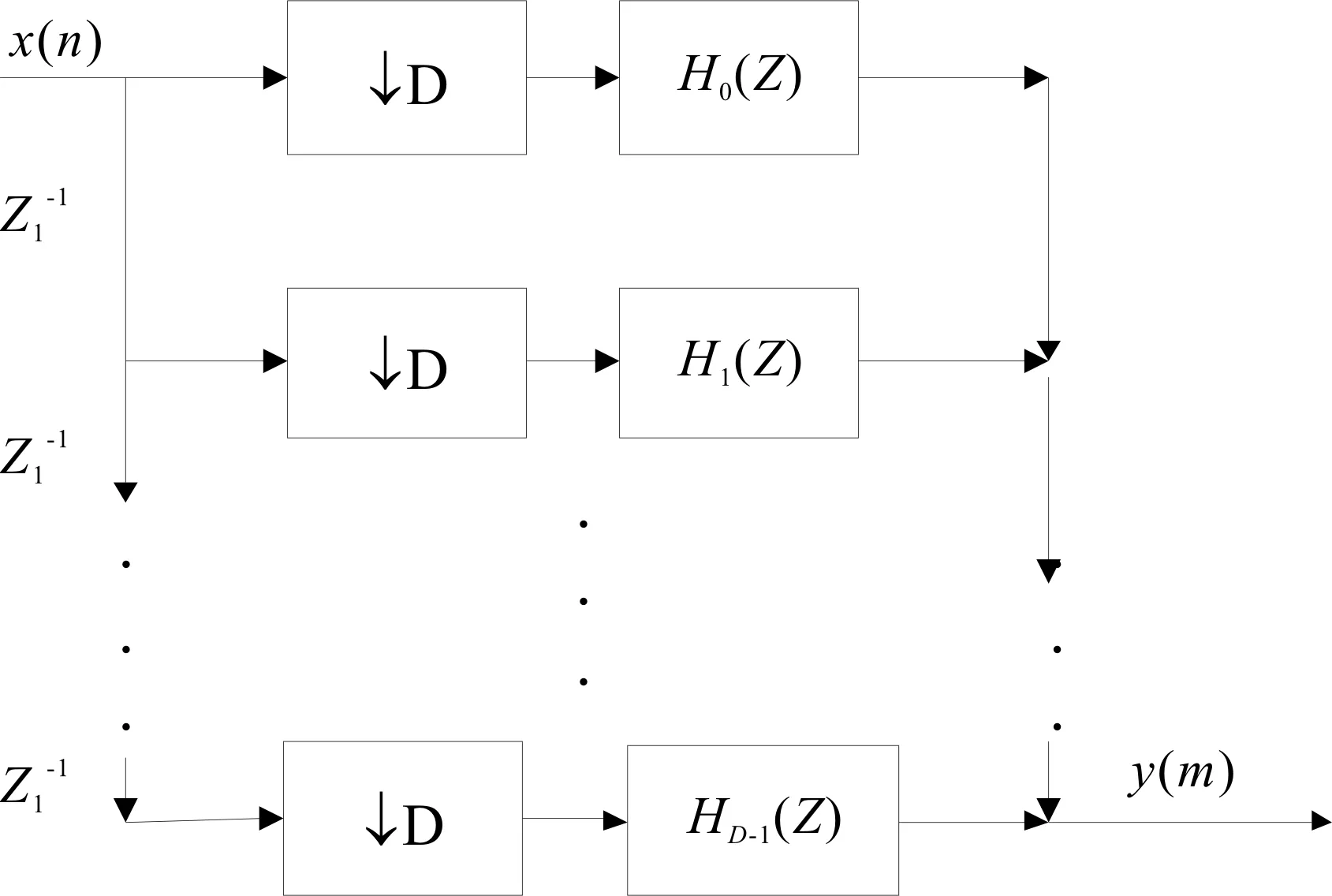
图2　取器多相结构的转换形式

此结构中，数字滤波在抽取之后进行，大大降低了对处理速度的要求。另一个好处是每一分支滤波器的系数由原有的N个，减少为M=N/D个，从而减少滤波运算累积误差，提高了计算精度，并可方便滤波器的实现。实现时，可采用如图3所示的换相形式：

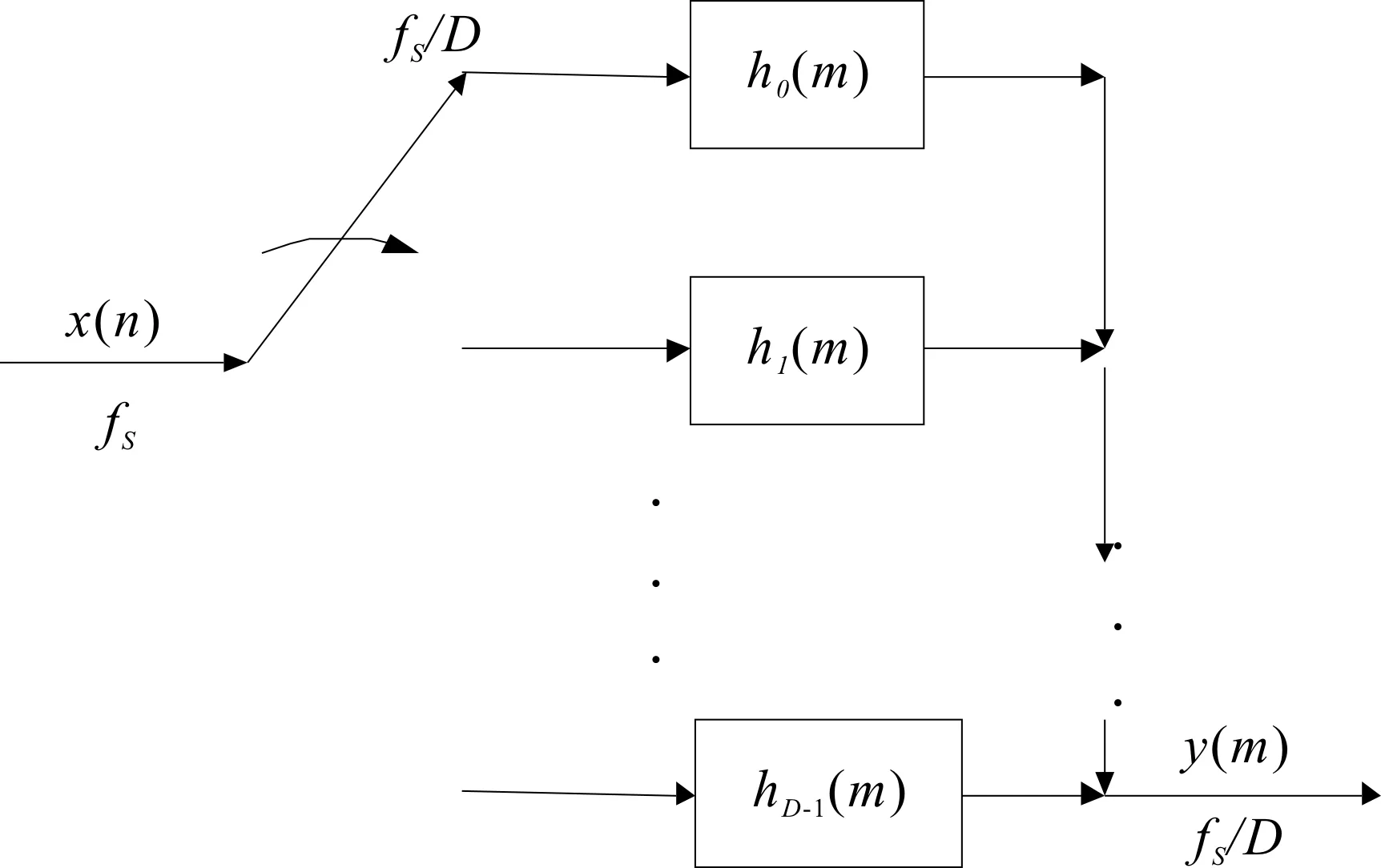
图3　抽取器多相结构的开关形式

设抽取器原始结构下，要求在采样间隔T秒内完成N次乘加运算，其计算速度要求为：

S1=Nfs(次乘加/秒)

(5)

采用多相结构后各分支滤波器hk(m)的阶数为N/D，输入数据率为fs/D，其计算速度要求为：

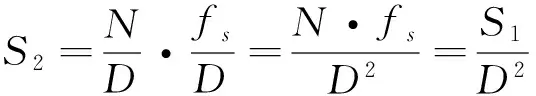
(6)

即只为原始结构滤波器速度要求的1/D2，当D较大时，对运算速度的要求将大大降低[4]。

2　实际抽取滤波器的实现

在实际数字下变频系统中，对于抽取滤波器的设计，可采用上述多相滤波结构高效的实现。

实际系统结构如图4所示，多个载波信号经过ADC处理后得到离散多载波序列；再经过两路数字NCO将其变至基带，输出相互正交的I、Q两路信号；最后通过多相结构的抽取滤波器，降低数据采样率，输出所需要的数字基带信号。

本文重点关注的是抽取滤波结构的设计，其需要将2载波的中频采样信号进行下变频，对输入信号需要进行4倍抽取(抽取倍数D=4)，使数据采样率由3.84M，降为0.96M。该抽取滤波器的处理时钟为245.76M。

由于抽取倍数较小，抗混叠滤波器可采用一个经典的FIR滤波器即可满足要求。FIR滤波器的设计方法很多，实际中使用matlab软件工具，根据系统的实际参数，可方便的得出满足需求的滤波器系数。根据实际数字下变频系统通带和阻带的要求，使用窗函数法，可设计出该FIR滤波器为32阶[5-6]，或者在Matlab中也可选用remez函数进行此种滤波器的设计[7]。

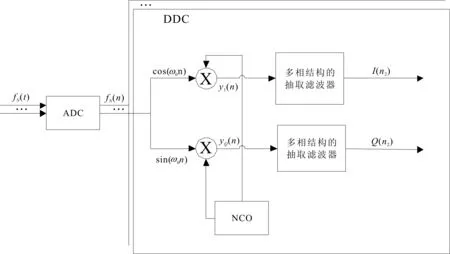
图4　采用多相处理结构的中频数字化接收机结构

考虑到由于处理时钟比输入数据速率快很多，可以将多相结构与多载波相结合，这样既可以充分利用处理速度的优势，又可节约硬件资源。

首先由时钟余量与处理时钟的关系：

Ds=fclk/Vdata

(7)

其中，Ds表示系统时针余量；fclk表示处理时钟频率；Vdata表示输入数据速率。可得该系统的时钟余量为64倍。

另外由时钟余量与载波数量的关系：

Ds=C×D×Dp

(8)

其中，C表示载波数，D为抽取倍数；Dp为一相需要处理的数据数。

将(7)式代入可得

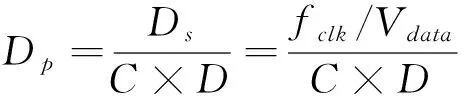
(9)

可得2载波4倍抽取时滤波器的一相需要处理的数据数为8。

其次根据多相滤波器设计原理，相数等于抽取倍数，而抽取滤波器系数：

N=P×Np

(10)

其中，N为滤波器系数；P为相数；Np为一相的除数。

若要充分利用时钟余量，可使一相的阶数等于一相需要处理的数据数，若两者无法做到相等，则会有时钟余量的剩余。

由此，该抽取滤波器为32阶，可分为4相，每相为8阶。对输入2载波信号，每载波每相需进行8次乘累加处理，充分复用后刚好可以把时钟余量用完。

具体实现结构如图5所示：

图5　多相结构的抗混叠滤波器实现形式

其中一载波一相的处理结构如图6所示：

图6抗混叠滤波器其中一相的实现结构

数据存储单元可用来缓存外部输入的数据，由时序控制模块控制在特定时刻输出I、Q数据。系数存储单元用于存放预先设计好的抗混叠滤波器的系数，其由控制模块控制按照特定时序输出与I、Q数据相对应的滤波器系数。乘累加单元分别接收I、Q数据和滤波器系数，并进行乘累加运算。寄存单元用于暂存滤波结果。

其特定的时序关系可按照图7来安排。

图7抗混叠滤波器多相结构的时序说明图

开关调拨到第二相，处理方式与第一相类似，依次取两个载波的8个I、Q数据分别与8个滤波器系数做乘累加运算，16个时钟周期后处理完毕。对第三相、第四相也是同样的处理过程。32个滤波器系数在4相处理中分别提取使用。

最终完成4相的处理后将各相滤波结果进行相加，并按照输入数据和滤波器系数的有效位进行适当的截位处理。再对2个载波的滤波结果对齐输出，并产生相应的使能信号。

3　结语

通过上述的分析，多载波的数字下变频处理使用多相抽取滤波器结构与多载波复用相结合来高效实现，既能够节约硬件资源又充分利用了系统处理时间余量。该方案在FPGA中硬件实现后能够达到满意的滤波和抽取效果。

[1] 向新.软件无线电原理与技术[M].西安：西安电子科技大学出版社，2008：1-2.

[2] [3][4]楼才义，徐建良，杨小牛.软件无线电原理与应用[M].2版.北京：电子工业出版社，2014：84-88，36-38，49-51.

[5] Uwe M B.数字信号处理的FPGA实现[M].刘凌，译.2版.北京：清华大学出版社，2006:99-101.

[6] 杜勇.数字滤波器的MATLAB与FPGA实现[M].2版.北京：电子工业出版社，2014:195-199.

[7] 陈怀琛.数字信号处理教程——MATLAB释义与实现[M].北京：电子工业出版社，2004:243-249.

[责任编辑、校对：郝杰]

Research on the Realization of Digital Down Converter System

SONGFei

(School of Electronic Engineering,Xi'an Aeronautical University,Xi'an 710077,China)

Under the SDR structure background,the paper studies the theory of digital decimation,and presents the scheme of digital down converter system,namely realizing four-times decimation through multi-partition structure and anti-frequency disturbing filter through FIR filter.In the meanwhile,it also realizes the combination of multi-carrier process and multi-partition structure through the system time margin,which can not only save hardware resources,but also make full use of system time margin to enhance resource utilization.Realizing the system in FPGA can generate the satisfactory decimation and filtering effects.

DDC;integral decimation;multi-partition structure FIR filter;multi-carrier combination

2016-07-19

宋飞(1981-)，男，陕西西安人，助教，主要从事数字中频与软件无线电研究。

TN924

A

1008-9233(2016)05-0056-04