数学思维活动的有效引领

陶玉霞

上好一堂课，上好一堂有效的数学思维探究课，是新一轮数学课课程改革的永恒追求。怎样通过科学、有序的教学活动，让知识背景、智力水平、个性品质各不相同的学生在数学学习中，实现“不同的人在数学上得到不同的发展”这一目标呢？

一、亲身实践，即兴生成

最有效的学习，是学生对学习过程的体验，学生只有通过亲身实践，将体验进行升华和内化，才能达到自主构建知识的目的。建构主义认为：学习是与一定的情境相联系，在实际有意义的情境下学习，可以使学生利用自己已有的认知结构中的有关经验，去同化和顺应当前学习的新知识，以达到学生建构知识的目的。

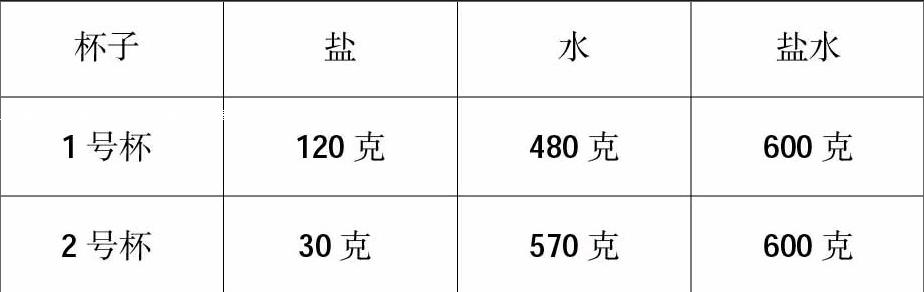
【案例1】教学“百分率”时，先用课件出示：人在海面上看书的情境，在西亚的南端，有一个死海，这里不长草，也没有动物生存，即使鱼儿在这里也会死掉，但是大人、小孩在海面可以躺着看书，也可以打上伞游玩，都不会沉下去。这到底是为什么？为了激发学生兴趣，我调制两杯盐水，各放入一个鸡蛋。学生观察发现，一个杯子的鸡蛋浮上来，另一个则沉下去，这是为什么呢？

请同学们根据表中提供的数据算出含盐率。

第一个杯子的含盐率高，所以浮上来，第二个杯子的含盐率低，所以沉下去。

一般海水的含盐率在3.5%左右，而“死海”的含盐率是22%，海水的比重大于人的比重，那么，人在海上看书就是轻而易举的事了。

新知识在故事化的情境中生成，对学生而言，这样的学习极富学习价值。科学与科普知识的融合，既增添了学生学习的乐趣，又让学生体会到可以用数学知识解释生活中有趣的自然现象。

二、猜想验证，构建模型

问题是探究性学习的核心要素。没有问题，就不存在探究。探究的问题要有价值性。教师要有意识地为学生创设问题情况，并通过点拨、启发、引导，促进学生积极思考，让他们自主发现并提出有价值的数学问题，使其产生强烈的求知欲望，同时培养他们的问题意识。

【案例2】教学“圆面积的计算”

首先让学生猜想和尝试推理。

师：圆面积的大小由什么来决定？（半径）

生：圆的面积由半径来决定（半径确定圆的大小）

师：计算圆面积肯定与半径有关。

以半径为边长的小正方形面积是r2，那么，大正方形面积是4r2，猜想一下，圆的面积同4r2比较，圆面积有多大？（通过观察、学生会说出，圆面积比3r2大，比4r2小，也就是比3个r2多一点）这样通过学生的观察和猜想，知道圆面积大约是3个r2多一点，为圆面积公式推导铺平了道路。同时建立起了r2是以半径为边长的正方形面积这样的模型，为学习圆面积计算奠定了基础。

接着再让学生动手学习圆面积公式，把准备好的圆平分成若干等份。要求学生把这些相同的图形换成已学过的图形。（长方形、三角形）

再引学生进行公式推导：

【评析】通过学生积极的参与，用猜想、验证、转化的思想自主动手探索思考，推出圆面积公式，验证自己的猜想，培养了学生思维的独创性。

三、自主探究，解惑释难

自主学习的关键在于学生的自主，因此，调动学生学习的积极性，给学生更多的自主权、选择权、支配权。其方法是：（1）先学后教。这种方法可以发挥学生的能动性和创造性，有利于学生自主学习的展开。教师点拨时必须做到知识的整体性和全局性。（2）把更多的时间和课堂留给学生。教师在课堂上应更多地采用师生对话和鼓励生生对话，为了保证学习效率，讨论与合作是两种好的学习方式，家庭作业可以布置得少一些。苏霍姆林斯基认为：只有当孩子每天按自己愿望随意安排时间，才能把学生培养成为聪明的全面的人。（3）设置疑难情境，引导学生去思考。（4）帮助学生排除一切干扰因素。当学生缺乏一定的能力时，教师要及时指点，防止学生浪费时间和精力，同时要对困难学生进行鼓励。

【案例3】教学“环形面积”

如，在教学“把环形剪拉成梯形，推导环形的面积公式”这节活动课时，部分学生受“把圆形剪拼成长方形可推导圆面积公式”的影响认为：可以把环形也剪成长方形进行研究，这时启发学生思考：如果把环形拉成长方形，那么圆形外圆周长和内圆周长分别相当于长方形的两条长，长方形的两条长应该相等。所以，这种方案不合理，需要修正。在教师的启发下，学生反思：把环形拉成梯形进行研究。学生在剪、拼、算、议的过程中得出这样的结论：环形的外圆周长和内圆周长分别相当于梯形的上、下底，环宽相当于梯形的高。根据梯形面积公式推出：

环形面积=（2πR+2πr）（R-r）÷2

=π（R+r）（R-r）

=π（R2-r2）

【评析】通过自主探究，让学生经历转化策略形成过程，使学生经历困惑，经历复杂的体验，产生猜想、尝试、验证的需要。突出学生的思维训练，开发儿童巨大的智力潜能，提高他们的数学素养，使他们感受创造数学的乐趣，更好地理解转化是学习数学最重要的策略。

四、合作交流，融会贯通

组织小组学习，让每个学生都发表自己的见解，对小组学习中出现的各种结果，运用分析、比较、讨论等方式进行集体交流，促进学生自我思考、积极交流、融会贯通。在各自得出的结论之间建立联系，以求得最佳的答案，并达成共识，得出结论。同时，建立生生、师生之间多维互动的合作交流方式，并充分发挥生生，师生之间的互补作用，使学生真正参与自主解决问题的全过程。

【案例4】如用24个棱长为1厘米的小正方体摆成长方体，能摆几种？表面积和体积各是多少？

你看出了什么？学生四人一组，动手拼摆、思考、计算，发现用24个小正方体摆成的长方体，表面积不相等，但体积相等。

【评析】通过合作学习，他们学会了操作、计算、找规律的数学学习方法，同时促进他们相互交流，取长补短，学会合作，培养良好品质。在合作交流中，教师要尊重学生的异见、宽容学生的误见、鼓励学生的创见，要重视学生在相互交往中表现出的尊重、沟通、包容、成果分享、互补、竞争的氛围，培养学生的合作意识和交往能力。

参考文献：

刘国文.习题教学：数学思维的有效引领[J].小学教学参考，2012（6）.