基于灰色理论与BP神经网络的油料消耗量组合预测

陆思锡，王 帅，熊 彪

（后勤工程学院，重庆 401311）

基于灰色理论与BP神经网络的油料消耗量组合预测

陆思锡，王 帅，熊 彪

（后勤工程学院，重庆 401311）

为了降低油料消耗量的预测误差，提高预测精度，将灰色预测模型所需初始数据少和BP神经网络预测模型非线性拟合能力强的优点结合起来，建立了基于灰色理论和BP神经网络的油料消耗量组合预测模型。通过引入单一预测模型的加权系数，更好地挖掘了两种预测方法所隐含的数据规律，使单一预测模型中存在的不确定性得到分散。算例结果表明，相较于灰色预测和BP神经网络预测的单一模型，组合预测模型的预测结果更贴近于真实数据，预测精确度更高、误差更小，将该模型用于油料消耗量预测是可行的。

油料；消耗量；预测；灰色理论；BP神经网络

1 引言

随着各种高新技术的不断运用，未来信息化条件下作战环境的不确定性更大，作战空间的转换也更加频繁，各种用油装备的油料消耗量也随之剧增，准确预测油料消耗量就成为油料储存、运输、补给等油料保障工作顺利展开的重要基础，同时也是制定油料保障计划、进行油料保障决策的重要依据。因此，对油料消耗量预测问题进行研究，为油料保障工作的实施提供科学依据就显得尤为重要。

常用的预测方法如多元回归预测、时间序列预测、灰色预测、BP神经网络预测等在预测精度以及预测范围上存在一定的局限性，例如灰色预测具有一定的预测区间［1-2］，神经网络预测存在易陷入局部极小值的缺陷［3］，且在历史数据较少时网络训练的外延性较差。为了提高预测的精确度，本文将灰色预测与神经网络预测的方法

结合起来建立基于灰色理论和BP神经网络的油料消耗量组合预测模型并进行算例分析。

2 油料消耗量组合预测模型的建立

2.1 油料消耗量组合预测的概念

组合预测是将多种预测方法进行融合形成一种新的预测方法，由Bates和Granger首次提出，通过适当的加权形式将单个预测模型有效地组合起来进行预测［4-9］。因此，油料消耗量组合预测就是以各种单一的油料消耗量预测模型获得的信息为基础，通过一定的方法将信息进行集成，使可能存在于单一预测模型中的不确定性进行分散［10］，降低油料消耗量预测的总体不确定性，提高预测准确度。

假设采用灰色或神经网络等单一预测方法得到的油料消耗量预测值为qi，组合预测值为Cq，则组合预测模型可表示为：

式中，n为单一的预测方法的种数；λi为每种单一预测方法的加权系数。

从上述分析可以看出，单个预测方法的加权系数对组合预测结果有重要影响，如果能够较好地确定加权系数，则可以充分挖掘不同方法所隐含的数据规律，利用各单项预测方法的优点，得到最好的预测效果。

2.2 灰色预测模型的建立

（1）对 X（0）进行累加，得到一个新的序列序列X（1）中任意值可表示为：

（2）检验X（0）的准光滑性以及X（1）的准指数规律。设若都成立，则认为具 有 准 光 滑 性 ；设若都成立，则认为具有准指数规律；当同时满足上述两个条件时，就可对X（1）建立灰色预测模型［10-12］。

（3）得到X（1）的紧邻均值生成序列。对X（1）数据序列中每组相邻的两个值进行平均得到一组新的值，由此构成一个新的序列则序列中的任意一个值可由下式来确定：

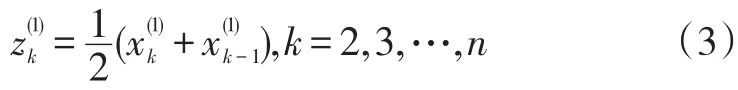
（4）建立X（1）的一阶微分方程。X（1）的一阶微分方程即状态方程，可表示为：

式中，a和u均为参数，该微分方程的时间响应式为：

将上式离散化，则有：

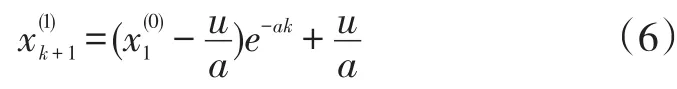
式中a和u的值可通过最小二乘法求得，令：

（5）得到油料消耗量预测值。将a和u的值代入式（7）中，得到序列对其累减进行数据还原，即得到预测值：

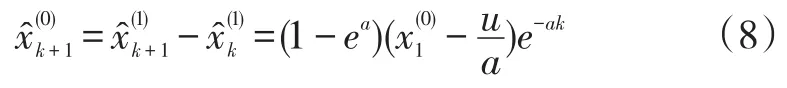
2.3 BP神经网络预测模型的建立

BP神经网络属于多层状型网络，使用梯度下降法将输入/输出问题转化为非线性优化问题，可获得从输入到输出的任意非线性映射［13-14］。利用BP神经网络对油料消耗量样本数据进行训练可通过以下步骤来实现：

（1）初始化权值wji、vj和阈值θ0，使其为均匀分布的较小数值；

（2）输入样本xi，计算各层输出。其中隐含层各神经元输出输出层神经元输出为

（3）计算输出层误差δ=（d-o）o（1-o），其中d为实际值，o为输出值；

（6）对剩余的训练样本数据重复上述步骤直至输入所有样本数据。根据误差计算公式（n为样本数）得到误差值，若E大于指定的误差值EZ，则返回到（2），直到E＜EZ。

2.4 组合预测模型的建立

灰色BP神经网络组合预测模型是对经过初始化处理的历史数据分别用灰色预测模型和BP神经网络进行预测，然后将预测结果进行线性组合并求出组合的权重，再利用组合模型对油料消耗量进行预测。设置BP神经网络为典型的三层结构，则组合预测模型由一个灰色预测模型和一个包含三层的BP神经网络预测模型构成。

上述模型是以λi为决策变量的优化模型，解此线性规划问题，可以得到两种预测方法在组合预测模型中的权值λ1和λ2，然后将权值代入式（1），利用组合预测模型对油料消耗量进行预测。

2.5 油料消耗量组合预测模型的预测步骤

（1）对样本数据进行处理。对于BP神经网络的样本数据，为加快网络学习速度，改善网络性能，以利于网络学习，需要构造输入数据和输出数据，并对其进行归一化处理，即：

对于灰色预测模型，直接采用原始数据序列进行预测。

（2）利用灰色预测模型和BP神经网络预测模型分别对样本数据进行预测，得到各自的预测结果和预测误差。

（3）将预测误差代入式（9）求出灰色预测和BP神经网络预测在组合预测中的权重λ1和λ2。

（4）利用步骤（2）中得到的两种预测模型以及步骤（3）中计算出的模型权重值对油料消耗量进行组合预测，得到预测结果。

3 算例分析

在某次岛礁进攻作战演习中，演习第1天至第10天的油料消耗量见表1，为了更好地制定油料保障计划，现利用建立的油料消耗量组合预测模型对演习第11天的油料消耗量进行预测。

表1 演习前10天油料消耗量

首先对样本数据进行处理，选取每连续5天的样本数据作为一组训练样本，连续5天之后的那一天的油料消耗量作为输出数据。按照式（10）对其进行规范化处理，使之变换到［0,1］之间，经过计算，得到处理后的5组训练样本输入数据和输出数据分别为：

然后按照灰色预测模型及BP神经网络模型的预测步骤对样本数据进行预测。其中，BP神经网络的训练参数设置为：隐含层函数为Sigmoid函数，输出层函数为线性函数，网络训练使用Levenberg-Marquardt算法，神经网络为5×3×1的BP网络，学习次数为1 000次，学习速率为0.001，学习目标误差设为0.000 001，通过5次训练收敛到设定的误差范围内，如图1所示。通过编程计算［15］，得到两种方法的油料消耗量预测值及误差见表2。

图1 BP神经网络训练误差收敛图

表2 灰色预测模型和BP神经网络预测误差

求解上式得到灰色预测模型和BP神经网络预测模型在组合预测中的权重分别为λ1=0.322，λ2=0.678，将其代入式（1），得到组合预测模型Cq=0.322q1+0.678q2，通过编程计算，得到预测结果见表3，预测结果对比如图2所示。其中，演习第11天的油料实际消耗量为4.235×105kg。

表3 不同预测模型预测结果（单位：105kg）

图2 不同预测模型预测结果对比

从表3数据和图2预测效果的对比可以看出，组合预测在油料消耗量预测中比单一方法预测的效果更好，能够更加真实地反映油料消耗的实际情况。

4 结论

单独采用灰色预测模型和BP神经网络预测模型对油料消耗量进行预测时，在预测区间、局部极小值等方面都存在一定的缺陷，增加了预测结果的不确定性。通过建立基于灰色理论和BP神经网络的油料消耗量组合预测模型，可以分散单一预测模型中存在的不确定性，从而提升油料消耗量预测的准确性。加权系数的引入，可以更好地挖掘灰色预测和BP神经网络预测所隐含的数据规律。通过对岛礁进攻作战演习油料消耗量的预测实例分析表明，组合预测模型提高了预测精度，预测结果比较理想，优于单一预测模型，因此，将基于灰色理论与BP神经网络的组合预测模型用于油料消耗量预测是可行和有效的。

［1］邓聚龙.灰预测与灰决策（修订版）［M］.武汉：华中科技大学程大学出版社,2002.

［2］刘思峰,党耀国,方志耕.灰色系统理论及其应用［M］.北京：科学出版社,2007.

［3］王洪元,史国栋.人工神经网络技术及其应用［M］.北京：中国石化出版社,2002.

［4］B H M Sadegh.A BP-neural Network Predictor Model for Plastic Injection Molding Process［J］.Journal of Materials Processing Technology,2000,103（3）：411-416.

［5］傅毓维,张凌.预测决策理论与方法［M］.哈尔滨：哈尔滨工程大学出版社,2003.

［6］韩晋,杨岳,陈峰,李雄兵.基于非等时距加权灰色模型与神经网络的组合预测算法［J］.应用数学和力学,2013,34（4）：408-414.

［7］马吉明,徐忠仁,王秉政.基于粒子群优化的灰色神经网络组合预测模型研究［J］.计算机工程与科学,2012,34（2）：146-149.

［8］张树奎,肖英杰,鲁子爱.基于灰色神经网络的港口集装箱吞吐量预测模型研究［J］.重庆交通大学学报,2015,34（5）：135-138.

［9］李晓利,王泽江.基于改进的灰色神经网络煤炭物流需求预测模型［J］.统计与决策,2015,34（5）：82-84.

［10］杨华龙,刘金霞,郑斌.灰色预测GM（1,1）模型的改进及应用［J］.数学的实践与认知,2011,41（23）：39-42.

［11］王龙,徐刚,刘敏.基于信息熵和GM（1,1）的上海市城市生态系统演化分析与灰色预测［J］.环境科学报,2016,36（6）：2 266-2 267.

［12］赵爱文,李东.中国碳排放灰色预测［J］.数学的实践与认知, 2012,42（4）：61-67.

［13］李松,刘力军,翟曼.改进粒子群算法优化BP神经网络的短时交通流预测［J］.系统工程理论与实践,2012,32（9）：2 045-2 049.

［14］刘宗磊,庄媛,张鹏程.基于径向基神经网络的Web Service Qos属性值组合预测方法［J］.计算机与现代化,2015,（12）：52-55.

［15］桌金武,李必文,魏永生.MATLAB在数学建模中的应用（第2版）［M］.北京：北京航空航天大学出版社,2014.

Combination Forecasting of POL Consumption Based on Grey Theory and BP Neural Network

Lu Sixi,Wang Shuai,Xiong Biao
（Logistical Engineering University, Chongqing 401311, China）

In this paper, in order to improve the accuracy in POL consumption forecasting, we combined the grey forecasting model withthe BP neural network forecasting model. Then by introducing the weighted coefficient for each individual forecasting model, we betteruncovered the hidden data pattern of the two and thus dispersed the uncertainty of the individual forecasting models. At the end, through anumerical example, we found that the combination forecasting model was more accurate and less erroneous than its two constitutingforecasting models and was feasible in forecasting POL consumption.

POL； consumption； forecasting； grey theory； BP neural network

TP183；E234

A

1005-152X（2016）09-0160-04

10.3969/j.issn.1005-152X.2016.09.033

2016-08-10

后勤工程学院青年科研基金（YQ15-410702）

陆思锡（1984-），男，四川武胜人，博士，讲师，研究方向：军队油料勤务。