基于表面波的塑性变形电磁超声定量无损检测

赵思琦,裴翠祥,肖　盼,陈振茂

(西安交通大学 机械结构强度与振动国家重点实验室，陕西省无损检测和结构完整性评价工程技术研究中心，西安 710049)



基于表面波的塑性变形电磁超声定量无损检测

赵思琦,裴翠祥,肖盼,陈振茂

(西安交通大学 机械结构强度与振动国家重点实验室，陕西省无损检测和结构完整性评价工程技术研究中心，西安 710049)

电磁超声具有非接触、易于激发和接收表面波等优点，探讨了基于表面波的金属材料塑性变形电磁超声无损检测及定量方法。首先，建立了电磁超声有限元数值计算模型，开展了电磁超声表面波探头的优化设计，并在此基础上搭建了基于电磁超声表面波检测的塑性变形检测试验系统；其次，采用具有不同塑性变形的单轴和双轴拉伸不锈钢试件，分析了塑性变形的大小和方向与表面波传播速度之间的关系。最后，通过电磁超声系统测量表面波在两个正交方向的传播速度，实现了对不锈钢试件双轴塑性变形的定量无损检测。

无损检测；电磁超声；塑性变形；表面波

塑性变形的存在对材料的力学性能有重大影响，在焊接构件的制造和热处理过程中尤为明显。在工作温度、工作介质及塑性变形的共同作用下，构件的抗疲劳强度、抗断裂能力、抗应力腐蚀开裂及高温蠕变开裂的能力都将大大下降，从而造成使用过程中的质量问题，甚至引发许多质量事故[1]。因此对塑性变形的定量无损检测具有重要意义。

塑性变形的传统检测技术,如X射线衍射法、金相分析法等在检测过程中会对结构造成一定的破坏，并且由于操作复杂、精度低等原因，其在实际工程中的应用受到了限制。与其他无损检测方法相比，电磁超声无损检测由于具有非接触性、灵活性、检测速度快、检测能力强大等突出优点，目前已经广泛应用于材料的无损评价和无损检测领域中。

笔者研究了基于表面波的金属材料电磁超声塑性变形测量方法，建立了相应的电磁超声有限元计算模型，进行了表面波探头的优化工作，搭建了塑性变形测量试验系统，分析了具有不同塑性变形的单轴、双轴拉伸不锈钢试件中塑性变形的大小和方向与表面波传播速度之间的关系，实现了对不锈钢试件双轴塑性变形的定量无损检测。

1　测量方法及试验系统

1.1塑性变形测量原理

根据声弹性效应，可将在试件表面传播的表面波波速和平面应力/应变场,由式(1)联系起来[2-3]:

(1)

式中：v1和v2分别为在ε1和ε2的作用下表面波在x1和x2两个方向上的传播速度;v0为无应变情况下的表面波波速;K1和K2为由材料决定的应变-声系数;ε1和ε2为均匀分布在材料表面的主应变(变形)场。

基于这一公式，就可通过测量两个主应变方向上的表面波波速的变化量来实现对两个主应变的估算。

图1　塑性变形测量试验系统

1.2试验系统

图1所示为基于电磁超声表面波检测的塑性变形测量试验系统，其主要由RITEC RAM-5000 SNAP电磁超声系统及相应的软件、示波器、滤波器、检测探头及试件等构成。在试验过程中由RAM-5000系统提供脉冲激励电流，通入了脉冲电流的激励探头会在试件表面激发出表面波信号，这一信号由同样布置在试件表面的检出探头接收，再经由滤波器滤波后通入到示波器中，从而实现表面波信号的检测。

为了实现表面波的激励与检测，试验过程中需要将如图1(b)所示的两个相同的表面波电磁超声探头相隔一定的距离放置在试件表面上。表面波电磁超声探头由方形铷铁硼磁铁以及如图1(c)所示的回折型线圈构成。图1(c)中的回折型线圈由线径为0.2 mm的漆包线绕制，共9匝，线圈总长为42 mm，宽度为23 mm。

2　表面波电磁超声探头的数值模拟

2.1数值计算模型为简化计算过程，在数值模拟过程中将实际的三维模型简化为二维有限元计算模型。简化模型的长度为120 mm，高度为25 mm。材料为铝，密度ρ为2.7×103kg·m-3，弹性模量E为6.97×1010N·m-2，泊松比ν为0.33，电导率σ为3.45×107S·m-1。表面波电磁超声探头中的永磁铁简化为z方向的大小为0.5 T的均匀静态磁场，激励与检出探头中的回折型线圈如图2所示，线圈长度L为40 mm，导线线径为0.4 mm，导线间的间距D为0.4 mm，线圈的提离均为1.75 mm，两个线圈间的距离为30 mm，通入线圈中的脉冲激励电流幅值为1 A。

图2　回折型线圈模型

2.2数值模拟结果

为了使模拟的表面波信号的幅值达到最大，通入激励探头中的脉冲电流的频率需要经过计算来选取[4]。最佳激励频率f是如式(2)所示的表面波波速v和线圈中导线间距D的函数:

(2)

当导线间距D为0.4 mm时，通过计算得到最佳激励频率约为3.61 MHz。为了验证最佳激励频率，分别选取低于和高于3.61 MHz的两个激励频率。在通入这三种频率的脉冲电流的情况下，距离激励线圈30 mm处的表面质点在z方向的速度信号如图3所示(旁边小图为局部放大图)。比较模拟信号中的表面波部分，可发现在激励频率为3.61 MHz时，表面波有最大的幅值，从而验证了最佳激励频率的正确性。

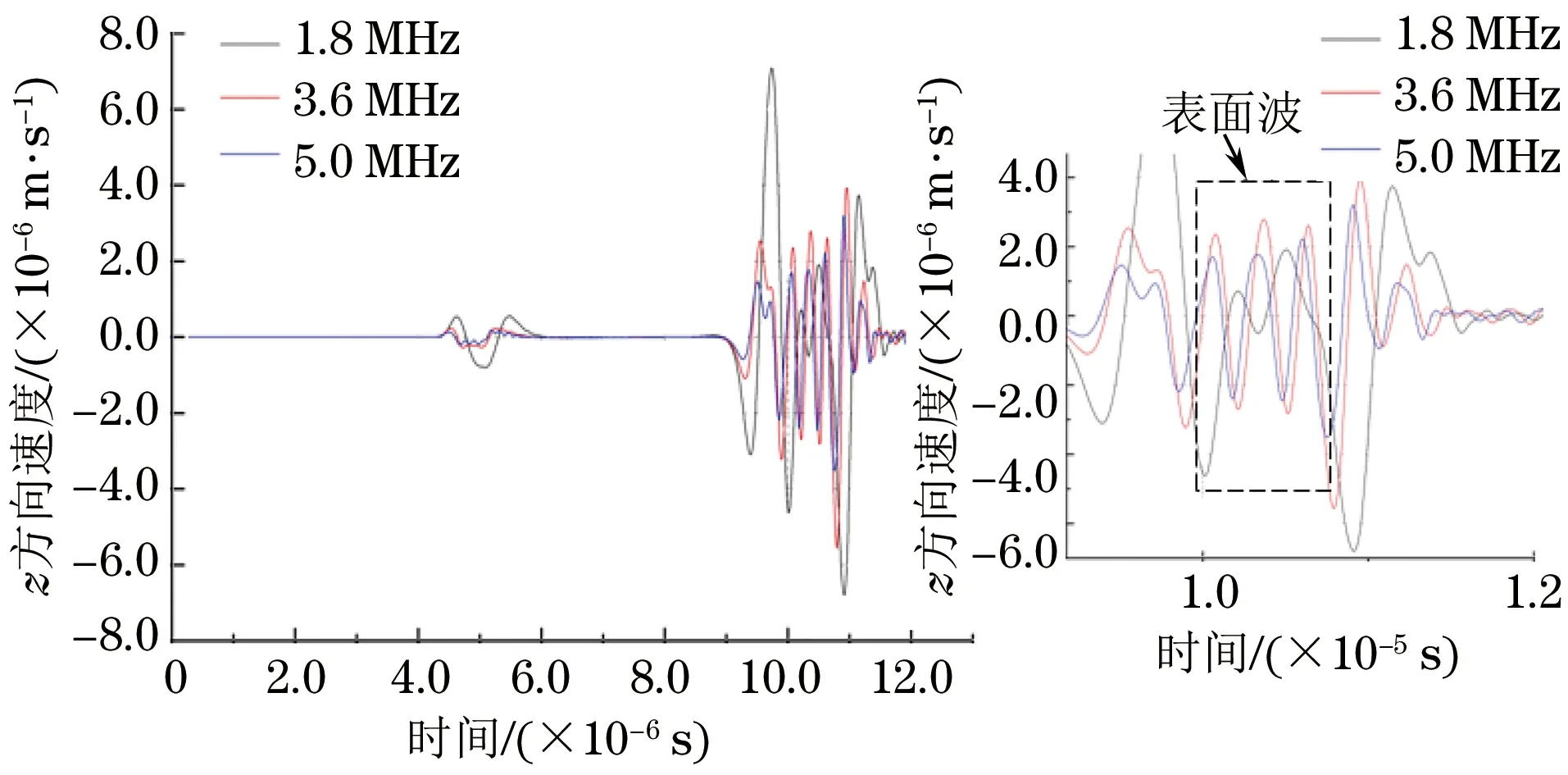
图3　不同激励频率下的模拟表面波信号

3　试验结果

3.1单轴拉伸试件的试验结果如图4所示，试验中需要进行测量的单轴拉伸试件呈狗骨型。试件由304不锈钢制成，密度ρ为8.03×103kg·m-3，弹性模量E为1.97×1011N·m-2，泊松比ν为0.33，电导率σ为1.1×106S·m-1。单轴试件的加载方向平行于试件的轧制方向，包括基准试件在内的8个试件具有从0%～15%的塑性变形(ε1)。

图4　单轴拉伸试件实物图

表面波在不锈钢中的传播速度为2 830.51 m·s-1，试验过程中使用的回折型线圈的导线间距D为3 mm，利用公式(2)可得出最佳激励频率约为0.5 MHz。其中激励与检出探头之间的距离保持为58 mm不变。表面波信号到达检出位置的时间随塑性变形的变化如图5所示(旁边小图为局部放大图)。从图中可以看出，在两个表面波探头的相对距离保持不变的情况下，表面波信号到达检出位置的时间将随着塑性变形的增加而减小。即，在不锈钢单轴拉伸试件中，表面波的传播速度将随着塑性变形的增加而增加。

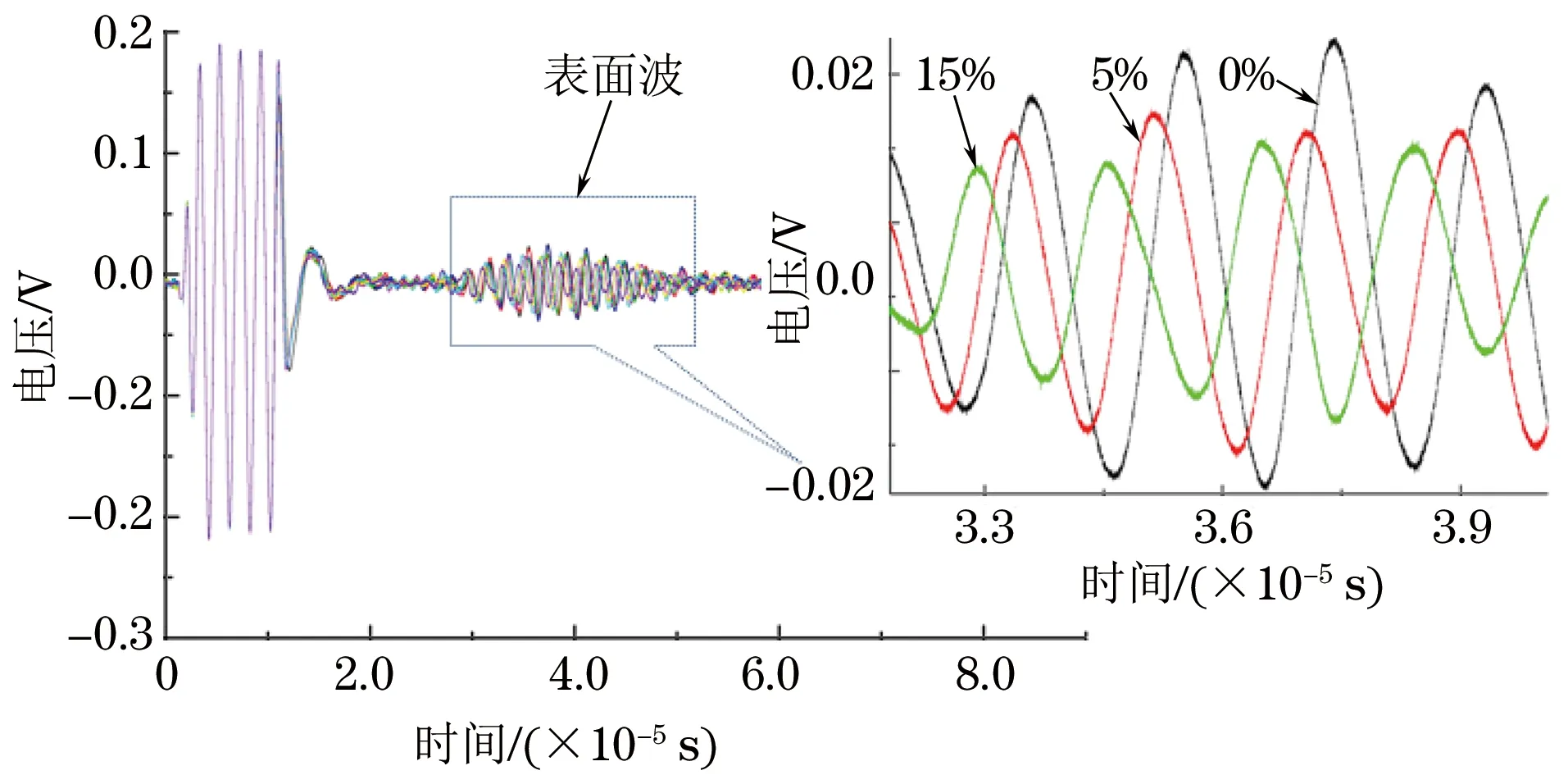
图5　单轴拉伸试件在不同塑性变形下的表面波信号

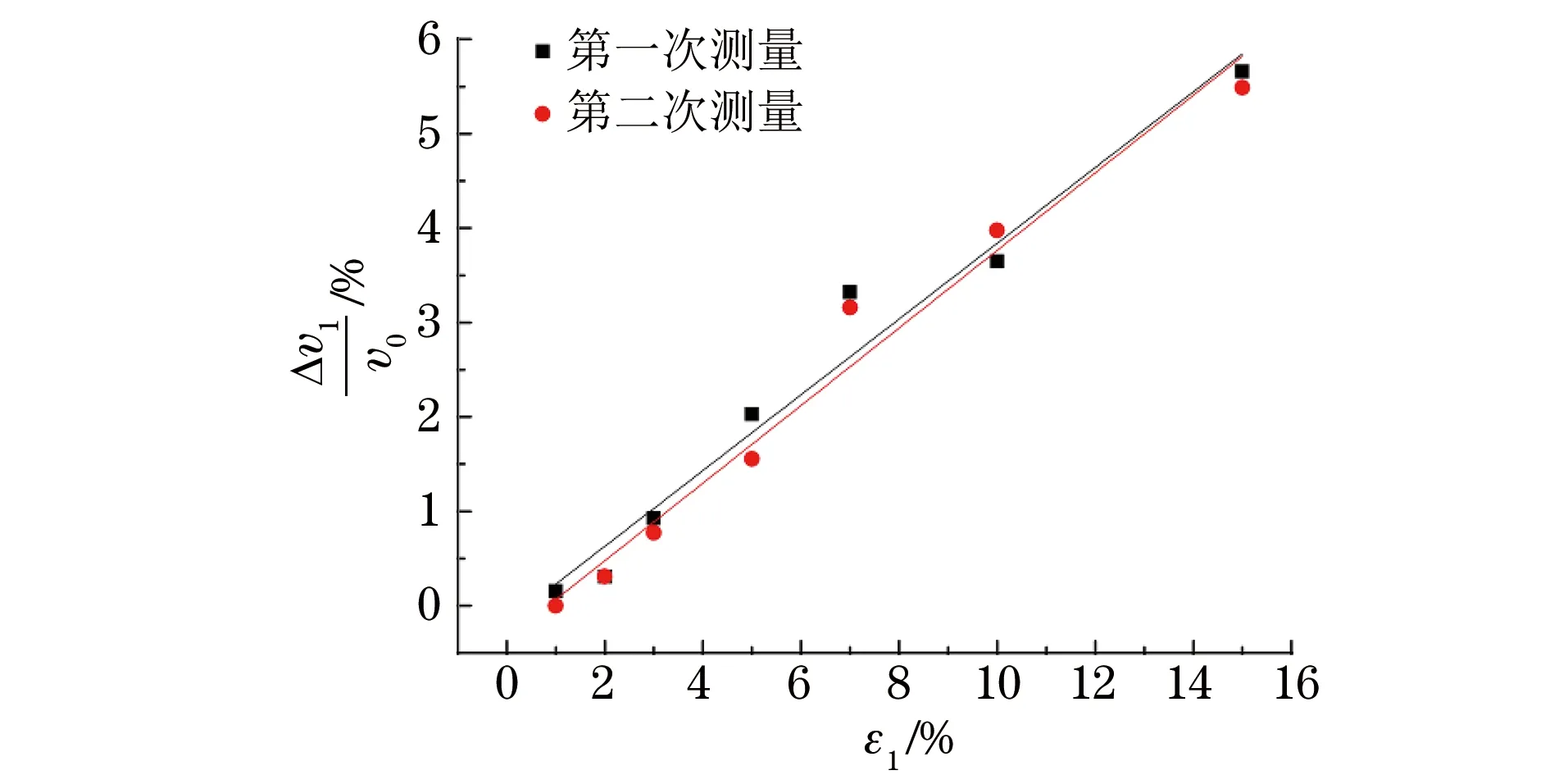
图6　单轴拉伸塑性变形与表面波波速相对变化量之间的关系

将通过试验获得的数据进行线性拟合[5]，得到了如图6所示的单轴拉伸塑性变形的幅值与表面波波速的相对变化量之间的线性关系。为了验证试验结果的一致性，进行了重复性试验，从图6中可以看出，两次试验结果的差值可忽略不计。根据式(1)，可以计算得到应变-声系数K1为0.401。

图7　双轴拉伸试件实物图

3.2双轴拉伸试件的试验结果

如图7所示的双轴拉伸试件呈十字形，试件材料与单轴拉伸试件相同，均为304不锈钢。经过双轴拉伸的4个试件中引入了1%～3.8%的塑性变形。双轴拉伸试件的试验采用与上节中单轴拉伸试件试验相同的试验装置及试验方法。然而由于加工工艺的限制，同一双轴试件在两个正交拉伸方向上的塑性变形不完全相同。因此，对于每一个试件都需要在两个正交方向上分别进行表面波信号的测量。同时为了便于总结双轴拉伸试件中塑性变形与表面波波速变化量之间的关系，在数据处理时还需要对两个方向上的塑性变形及相应的表面波波速的变化量分别求取平均值。

利用与上节相同的数据处理方法，得到了双轴拉伸试件中表面波波速的相对变化量与塑性变形之间的关系。如图8所示，两条拟合直线分别表示了单轴、双轴拉伸试件中表面波波速的相对变化量与塑性变形的线性关系。由于双轴拉伸试件中存在ε2的影响，可以发现图8中的双轴拉伸试件的线性关系线的斜率要比单轴拉伸试件的斜率大。结合上节中K1的计算结果，利用式(1)可以得到应变-声系数K2=0.313。

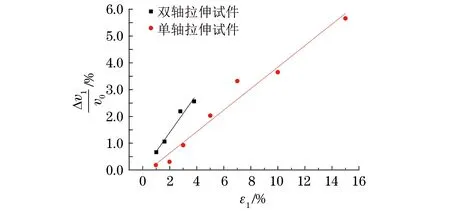
图8　表面波波速相对变化量随单轴、双轴塑性变形的变化规律

将在双轴试件的两个正交的拉伸方向上测量得到的表面波波速相对变化量,代入已经求得系数K1和K2的式(1)中，即可得到双轴试件在两个拉伸方向上塑性变形的计算值，表1分别给出了4个双轴拉伸试件中塑性变形的实际值及计算值(右上角不带撇的符号表示实际值，带撇的符号表示计算值)。比较表1中数据可以发现，除1号试件以外，其他试件中计算得到的塑性变形和相对应的实际塑性变形之间的误差处于可以接受的范围内。而对于1号试件，由于试件的塑性变形较小，因此计算结果很容易被测量误差影响，从而导致计算结果和实际的塑性变形之间存在较大误差。

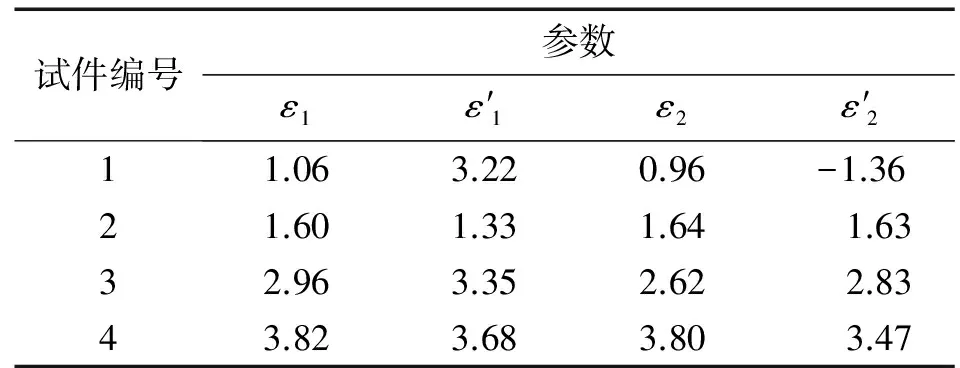
表1　双轴拉伸试件的实际以及计算塑性变形

4　结语

提出了一种基于表面波的金属材料塑性变形的电磁超声无损检测及定量方法，建立了电磁超声有限元数值计算模型，开展了电磁超声表面波探头的优化设计，搭建了基于电磁超声表面波检测的塑性变形检测试验系统。对具有不同塑性变形的单轴和双轴拉伸不锈钢试件进行了试验测量，测量结果给出了塑性变形与表面波波速相对变化量之间清晰的线性关系。基于试验结果给出了塑性变形与表面波波速相对变化量之间的关系式，实现了对不锈钢试件双轴塑性变形的定量无损检测。在下一步的工作中，将进一步优化电磁超声表面波探头，获取频率更高的表面波，从而提高文中所用方法的精确度及分辨率。

[1]林立华，陈立功.残余应力测量技术现状及其发展动向[J].机械，1998,25(5):53-57.

[2]JOHSON G C. Acoustoelastic theory for elastic plastic materials[J]. Journal of the Acoustical Society of America, 1981,70:591-595.

[3]RAVI-CHANDAR K. Progration of ultrasonic plane waves in a plastically deformed medium[J]. Review of Progress in Quantitative Nondestructive Evaluation,1993, 12:2083-2089.

[4]申建中，张仲宁，张淑仪. 表面波电磁声换能器的设计[J].应用力学,2007,26(4):197-201.

[5]PEI Cui-xiang, DEMACHI K.Numerical simulation of residual stress measurement with acoustic wave[J]. E-Journal of Advanced Maintenance,2011,2:160-167.

Plastic Strain Measurement with Electromagnetic Acoustic Testing Method Based on Surface Wave

ZHAO Si-qi, PEI Cui-xiang, XIAO Pan, CHEN Zhen-mao

(Shanxi Engineering Research Center of NDT and Structural Integrity Evaluation, State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi′an Jiaotong University, Xi′an 710049, China)

Due to the non-contact feature and the ability of easily generating and detecting surfacewaves, in this work, electromagnetic acoustic transducers (EMATs) are studied for the nondestructive testing and evaluation of plastic strain in metal materials with using surface waves. Firstly, a numerical model based on finite element method (FEM) is established for EMAT simulation and optimization. And a surface-wave EMAT experimental system is constructed for plastic strain measurement. Secondly, the relationship between the magnitude and direction of the plastic strain and the velocity of the surface wave is studied by EMAT with using uniaxial and biaxial tensile stressing of stainless steel samples with various plastic strains. Finally, a quantitative NDT of biaxial plastic strain in stainless steels was realized with measuring the velocities of surface waves in two orthogonal directions by EMATs.

Nondestructive testing; EMAT; Plastic strain; Surface wave

2016-06-22

赵思琦(1993-)，女，硕士研究生，主要从事电磁无损检测理论和试验研究工作，E-mail: zhaosiqi@stu.xjtu.edu.cn。

陈振茂(1964-)，男，教授，E-mail: chenzm@mail.xjtu.edu.cn。

10.11973/wsjc201610007

TG115.28

A

1000-6656(2016)10-0025-04