中国收入分布演化实证及机制研究

许 研，王有贵



中国收入分布演化实证及机制研究

许 研，王有贵

(1. 北方工业大学经济管理学院 北京石景山区 100144；2. 北京师范大学系统科学学院 北京海淀区 100875)

已有工作发现1998～2002年期间的中国收入分布呈现幂律分布特征。利用1988、1995年China Household Income Projects两次调查数据进一步检验了幂律出现前收入分布的演化过程；并确定了幂律尾出现的时间为20世纪90年末期。经济分析表明这一时期主要的收入影响因素是资本收入的出现。因此在Gibrat模型的框架下，增加了部分群体遵循资本收入变动特点的假设。仿真结果的短期收入分布呈现两段式lognormal分布，长期收入分布尾端呈现幂律分布。这表明资本收入是收入分布形式发生演化的重要条件。

分布演化实证; Gibrat模型; 个人收入; 幂律分布

个人收入分布是社会科学领域最早发现的幂律分布现象之一。早在1897年，意大利经济学家Vilfredo Pareto发现意大利地区各个收入规模上的人口分布服从Pareto分布，即幂律分布(power law)[1]。在其后的一百多年中，来自欧洲、美国、日本、巴西、印度，包括中国的收入分布实证工作都无一例外地发现了幂律分布特征[2-7]。但是对于个人收入的幂律分布是如何演化而来，并且这样的演化过程对幂律形成机制有怎样的启示等问题，目前还缺乏实证和理论研究。

中国居民经历的经济体制改革带动了收入来源和收入变动方式的多样化发展，为收入分布的演化过程研究提供了珍贵的样本。本文以20世纪80年代末至21世纪初中国居民收入数据为对象，分析中国收入分布幂律尾的演化过程，并结合这一时期我国经济制度和个人收入的变动特点探讨幂律分布可能的形成机制。

1 相关研究

由于经济体制的独特性，中国的收入分布形式备受瞩目。文献[8]发现1987年的江苏省个人收入分布整体服从Gamma分布；文献[9]发现1983～1986年辽宁省个人收入分布整体服从拟合优度逐渐增大的Lognormal分布；文献[10]分析发现1985～2001年的中国收入分布一直具有Lognormal分布的形式。文献[7]发现1998～2002年中国收入分布的中低收入部分服从Lognormal分布，并在高收入部分首次发现了幂律分布。该发现在文献[11]的工作中得到了验证，该文利用2005年中国收入数据研究Double Powerlaw- Lognormal分布特征时发现，高收入尾端呈现了明显的幂律分布特征[11]。已有工作表明，中国个人收入的幂律分布特征并非一直存在，只出现在20世纪90年代末以后的收入数据中。目前还缺乏对于幂律分布出现前收入分布的演化过程及幂律尾出现时间的实证研究。

对于Lognormal分布如何形成幂律分布的理论解释主要来自Gibrat模型及其衍生模型。1931年提出的Gibrat模型将经济系统中个体收入表示成初期收入与一系列收入增长率的乘积，并假设各期收入增长率独立且同分布，根据中心极限定理，收入服从Lognormal分布[12]。在Gibrat模型的基础上进行扩展并生成幂律分布的理论工作很丰富。文献[13]在个体收入的演化过程中设置阈值防止收入较低的个体继续降低收入。这种规则被证明可以形成幂律分布；文献[14]证明了当个体存在生灭过程时收入分布近似幂律分布，如果某收入区间内新旧个体的变动概率小于收入增长率，幂律分布形式不变，反之，幂指数变化。文献[15]用数学解析方法证明了当收入增长率的方差非常大时Lognormal分布近似幂律分布；文献[16-17]论证了当公司规模增长率的方差随着公司规模以幂律形式递减时，公司规模服从幂律分布；文献[18]研究发现由于特大城市行业的多样化降低了经济波动的风险，因此城市规模的增长率服从同分布的假设不能在所有城市中成立，对于特大城市，当增长率的方差与城市规模成反比时，城市规模排名分布服从zipf-law；文献[19]发现在Gibrat模型的框架下，将条件放松至收入增长的时间间隔服从指数分布，那么收入分布将出现幂律尾。以上工作虽然给出了Lognormal分布向幂律分布演化的微观个体变动机制，但是它们是否符合中国经济体制改革中居民的收入变动特征？如何基于中国的经济制度和收入变动特点设计更合理的收入幂律分布理论解释？将是本文力图解决的问题。

2 中国收入分布演化的实证分析

已有的工作已经证实了我国的个人收入在1998～2002年期间，服从Lognormal分布加幂律尾的两段式分布[7]。本文将利用更丰富的数据，检验1988～2002年之间收入分布形式的演化过程。

2.1 数据及数据处理方法

收入数据来自China Household Income Projects (CHIPS)1989年、1995年及2002年的3次调查。1989年的样本包含67 186个农村家庭和34 945个城市家庭，1995年包含了65 000个农村家庭和35 000个城市家庭。2002年的调查数据包含37 969个农村居民样本、20 632个城市居民样本和5 327个农村迁入城市居民样本。每次调查都涵盖了20个以上省份，保证了数据在地理区域上的全面性。其中，1989年调查得到1988年的收入数据，1995年调查得到1991、1993、1995年收入数据，2002年调查得到1998～2002年收入数据，其中1988年、1995年和2002年的数据是基于家庭的记账记录，1991年、1993年、1998～2001年的数据基于家庭成员的回忆记录。

本次调查中收入的构成依据国家统计局(national bureau of statistics, NBS)的定义标准，即各种主要收入、类收入、政府补贴和政府转移收入、减税收入。主要收入类型包括工资、自由职业的净收入、津贴、退休金、利息收入和投资的净收入等。类收入指自住房节省的租金等变相收入。所有的收入都以当年的消费价格指数CPI进行了调整，以消除通货膨胀的影响。值得说明的是，由于某些年份的调查对象为家庭，为了得到个人收入数据，将家户数据平均除以家庭的成人劳动力数量，再把平均值付给每个成人劳动力，从而近似作为家庭中的个人收入数据。具体的计算公式为，其中代表家庭的总收入，代表家庭人口数，其0.66次幂代表近似家庭的成人劳动力数量[20]。由于每次调查的样本基数有较大差异，本文只计算收入的人口概率密度分布。

2.2 实证结果

为了更准确地得到收入分布函数形式，本文对收入的累积概率密度分布(CDF)进行拟合。一方面由于CDF是概率密度累加的结果，可以剔除很多统计波动，统计特征更明显；另一方面，本文非常关心高收入人口分布，但该区域概率密度极小，在收入概率密度分布(PDF)中很难展示其分布特点。

文献[8-9]的实证工作结果均显示20世纪80年代的中国收入分布整体服从Lognormal分布。为了保证工作的延续性，首先假设1988年的整体收入分布服从Lognormal函数。如表1所示，虽然OLS方法(注重峰值拟合)和MLE方法(更侧重两翼拟合)[21]的拟合结果均显示拟合结果通过了卡方检验，但是将拟合曲线与真实数据放在图1中比较分析可见实证数据形成的CDF分布尾部保持着一定的曲度。高端收入与中低收入部分无法整体服从同一Lognormal分布，假设不成立。这一结论与文献[2]一致，在该工作发现Lognormal不适合作为整体分布的拟合函数，在其展示的1992年收入分布曲线中有明显的转折趋势。

表1 1988年收入分布的对数正态Lognormal分布拟合结果

结合1998～2002年中国收入分布服从Lognormal+幂律的两部分分布的实证结果[7]，本文对1988年的收入分布进行两部分分布拟合。利用文献[22]确定幂律分布转折点的思路，进行了如下设计：首先，选定[0,]中低收入分布的概率密度数据进行拟合，逐渐提高扩大拟合范围。对每个范围内的收入分布都进行Lognormal的拟合。根据MLE拟合原理，如果与真实的分布转折点重合时，MLE拟合可以给出最接近真实的分布参数，如果偏离真实点，拟合参数的偏差会迅速变大。因此，真实点的位置就是拟合函数与真实分布的“距离”(“距离”通过ks检验测量)最小的一次拟合对应的。确定后的两部分分布的转折点，如表2所示。对于高端收入分布拟合，虽然近期有工作利用4参数Modified Gaussian、Double Powelaw-Lognormal等函数较好地拟合了中国的收入分布[11,23-24]。但多参数函数易出现拟合算法无法达到整体最优等问题[1]，同时一些参数的经济意义不明确，不利于构建理论模型。因此，本文选取了3种同样具有大量实证工作支持的2参数函数：Lognormal、e指数和幂律函数[3-5]。拟合结果显示，虽然都通过了卡方检验，但幂函数的拟合效果稍差，Lognormal函数的拟合效果最好。利用相似的方法验证了1991、1993、1995年的收入分布形式，拟合结果表明它们均服从两段式Lognormal分布，如表2与图2所示。可以得出结论，1988～1995年的中国收入没有出现幂律尾分布，但中低端与高端呈现了不同的Lognormal分布形式。两段Lognormal分布的均值都具有逐年增大的趋势，中低端Lognormal分布的方差随时间明显增大，高端Lognormal分布的方差则没有变化。收入分布具有整体增长，且分布形式更加分散的趋势。

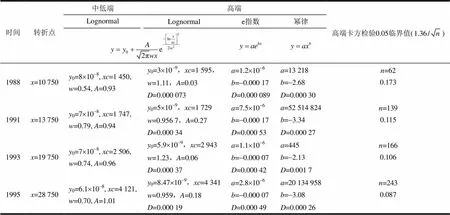
表2 收入分布的两段式拟合结果

结合1999～2002年的收入分布拟合结果[7]，我们得到了1988～2002年的中国收入分布特征及演化趋势，如图2所示。我国的收入分布在20世纪80年代初中期整体服从Lognormal分布，但到了20世纪80年代末开始呈现了一个高收入和中低收入部分服从不同参数的两段式Lognormal分布；而进入20世纪90年代末期，收入分布的高端演变为幂律分布，幂指数的范围-3.6～-4.2[7]。幂律分布的形成时间约为20世纪90年代中后期(1995～1998年间)。

3 幂律分布出现的经济解释

收入分布幂律尾出现的20世纪90年代中后期，中国居民尤其是高收入群体的收入来源和收入增长方式都发生了巨大的变化。

首先，非工资收入正成为一些家庭的主要收入来源，尤其是高收入家庭[25]。根据文献[25]的定义，非工资-私营收入包括商业经营收入、资本投资收入。其中商业经营收入主要包括个体经营收入和私营企业主收入；资本投资收入主要包括利息、股份、房租等收入[26]。改革开放前很长一段时间，工作单位为劳动者提供较广泛的福利，以现金形式发放的收入很少，所以居民几乎没有多余的财产。据统计，20世纪70年代末，家户储蓄总额不到国民生产总值的7%。并且，银行储蓄是家户资本收入的唯一来源。改革开放初期，私营收入仍可以忽略不计。直到1990年和1991年上海和深圳股票交易所分别成立，金融市场的出现为资本投资提供了多种多样的投资机会。20世纪90年代末，住房制度改革进步完成，催生了房地产投资市场和租赁市场。在我国房租是最大比例的资本收入，占53%[26]。与此同时，国企改革导致私营、个体经营比例提高；国有企业削减福利，私人保险行业出现，提供了另一种重要的资本收入来源。投资渠道的出现，导致这一时期资本收入和商业经营收入开始增长，并成为了有些家户的主要收入来源，尤其是那些高收入家庭[25]。

其次，收入变动出现新特点。众多实证研究表明，工资收入和资本收入的增长方式不同。文献[27]认为工资收入的增长与资本或企业经营收入的增长相比非常缓慢。文献[28]认为经济的增长带动了收入的增长，收入增长过程使精英人群受益，即人口中最富有的0.001%。因为精英人群主要从资本投资和商业经营中获得收入。实证数据也显示我国的低收入居民不仅在收入数量上与高收入居民有着悬殊的差距，其收入增长慢于高收入居民[29]。此外，一些有关收入差距的实证研究也能发现资本收入快速增长的特征。文献[30]发现资本收入对收入不平等的边际影响力远大于劳动收入。2013年文献[26]的工作中发现在中国西部的欠发达地区，资本和商务收入比例很低；较发达的沿海地区资本收入和商务收入的比重高。资本和商务收入比重大的地区不平等程度大[26]。在经济物理研究领域，Equiluz-Zimmermann 模型及其改进模型[31-32]也论证了由于羊群效应及信息传播速度的影响，资本市场的收益呈现差异较大的幂律分布特征。总的来说，资本收入的出现，以资本收入为主的群体逐渐增多，资本收入快速的增长方式是幂律出现前后我国居民收入变化的主要特点。

4 个人收入的演化模型

Gibrat模型是目前解释人类经济行为偏峰分布的一种重要的理论模型。它将收入表示成初始收入和一系列增长率的乘积，有：

对式(1)两端取对数可得：

并假设收入的增长率是与初始收入水平无关，独立同分布的随机变量，根据中心极限定理，多期演化后的收入分布服从对数正态分布。

Gibrat模型成功地解释了中低收入人群(占总人口95%～99%，劳动收入群体)的对数正态分布，包括中国在内的世界很多地区的收入分布都呈现了这一分布形式。它的缺陷在于无法解释存在于收入分布尾部的幂律分布。根据经济分析，资本收入和资本收入的快速增长特点与幂律分布的出现存在关系，本节将基于这两个收入特征对Gibrat模型进行改进。

4.1 模型假设

在Gibrat模型的框架下，本文假设部分收入高并进行资本累积的个体开始以资本收入作为主要收入来源。以下是关于资本收入、资本投资回报率和资本收入群体进入方式的三方面假设。

1) 资本收入。经济系统中资本收入与累积资本量和投资回报率有关。

将式(4)代入式(3)，并假设投资回报率是一个随时间收敛的函数，求导可得每期的资本收入变动的表达式为：

与劳动收入变动相比，资本收入的变动率不仅与资本投资回报率还与前一期收入有关。

2) 资本投资回报率。由于不断有个体进入资本收入群体，该群体可以看作一个投资者和资本量都不断增加的开放系统。根据凯恩斯的资本边际效率观点：①投资增加会引起资本品供给价格的上升，资本成本增加，投资的预期利润率下降；②投资增加会增加产品数量，导致产品市场价格下降，投资的预期利润率下降。此外，内生经济增长理论认为物力资本投资不断增加，导致其与劳动资本不匹配，也会严重地影响产出。因此长期来看，整个社会的平均投资回报率随着时间增长缓慢下降。

根据文献[33]各国统计年鉴计算的中美日三国投资回报率的演化趋势，将投资回报率的随时间的变动表示为：

3) 进入资本收入群体的方式。设计两种方式：①从短期来看，获得较高收入水平并可以将其进行资本投资的人数是等可能的。假设进入资本收入群体的人数服从时间[1,]的均匀分布。②长期来看，这种逐渐进入方式可以忽略不计。在较长的时间窗口中观察资本收入群体，个体的进入方式近似一次性同时进入。

4.2 数值模拟

对Gibrat模型、资本收入a模型和b模型进行仿真分析。首先设定仿真系统内个体总数为=50 000，每个个体的初始收入同为=3 000。根据文献[34]的有关收入增长率分布的实证工作结果，假设个体收入增长率服从均值为0、方差为0.042的Laplace分布。如图3所示，经过20轮的收入增长，收入分布就呈现了典型的对数正态分布，角图中是图3的概率密度分布形式。

资本收入模型假设初期的个体收入已出现了差异，收入分布服从=3 000，=0.5，=300的Lognormal分布。大部分个体收入演变规则与Gibrat模型相同，小部分资本收入群体的收入规则有所不同。每一期进入资本收入群体的个体数=5。资本投资回报率随着时间逐渐减小。根据资本收入变动特点，初始投资回报率应明显高于劳动收入增长率的均值；并且为了保证高收入部分与中低收入部分不出现断层，设置参数=0.2，=3。如图4a所示，经过多轮收入增长，收入分布呈现与1989～1995年中国收入分布相似的两段式Lognormal分布的形式。

考虑到从长期来看，时间观察窗口拉长时，个体进入资本收入群体的方式近似一次性同时进入。因此，资本收入b模型假设系统运行初期一次性进入资本收入群体的个体数=5 000；为保证高收入与中低收入部分不断层，设置参数=0.1，=3；其他条件与a模型相同。如图5a所示，经过更多轮的收入增长，收入分布的高端在横纵坐标为双对数的坐标系中呈现一条明显的直线，即服从幂律分布。但与a模型不同，高收入幂律尾分布受参数的影响较小。这是由于模型a中个体逐渐进入资本收入群体，随时间递减的投资回报率使个体的起始回报率差异较大。因此，越大，个体收入的分化程度越高，Lognormal分布的方差越大。相比之下，模型b中一次性进入资本收入群体的个体的初始回报率相同，参数的影响力有限。

图5b给出了不同系统运行时间下的收入分布变动关系图。与模型a相似，由于投资回报率的变动幅度随系统运行时间以负2次幂的速度递减，因此随着系统运行时间的延长，收入分布更加分散，收入不平等程度增加，幂律分布的幂指数绝对值随着时间增加而减小。这一规律也解释了为什么从世界范围来看，中国等发展中国家的幂律分布的幂指数较高(3.6～4.2)[7]，而日本、美国等资本收入出现早的发达国家的幂指数较低(1.5～2.2)[2-6]。

5 结束语

收入分布不仅是收入不平等程度的一种更具象的表现形式，而且是分析收入不平等成因的重要途径[1-2]。收入的幂律分布特征则意味着更加悬殊的个人收入差距以及极富人群的出现，因此对其形成机制的研究就愈发显得重要和迫切。本文结合已有工作，共利用1988年、1995年以及2002年CHIPS的三次入户收入调查数据，对中国收入幂律分布出现前收入分布的演化过程进行了实证分析。发现我国的收入分布经历了整体服从Lognormal分布，两段式Lognormal分布，再到高端出现幂律分布的过程。

20世纪80年代～90年代中后期，收入分布没有出现幂律，也没有遵循一致的Lognormal分布。这说明在经历了改革开放早期私有制经济的初步发展之后，个体收入已不再一致地符合增长率独立同分布的劳动收入特点。引入资本收入假设的Gibrat模型仿真结果表明，两段式Lognormal分布正是个体逐步进入资本收入群体，逐渐调整收入来源的过渡期的表现。

20世纪90年代后期至今，我国收入分布出现的幂律分布正是私营、个体经营比例提高，股市、保险、房地产租赁等资本收入快速发展的体现。仿真结果表明，资本收入的出现及其高回报率、平均回报率递减、非独立变动等特点是幂律分布出现的主要原因。而幂律分布形式与投资回报率随时间递减规律有关，递减速度越快，幂指数越小，收入不平等程度增大。因而，与收入投资回报率递减直接相关的外部投资量持续增加，技术进步速度缓慢等现象都是加速我国收入不平等程度扩大的主要原因。

本文的研究工作得到北方工业大学科研启动基金(2012-25)的资助，在此表示感谢。

参 考 文 献

[1] PINTO C, MENDES LOPES A, MACHADO J A. A review of power laws in real life phenomena[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(9): 3558-3578.

[2] GUO Q, GAO L. Distribution of individual incomes in China between 1992 and 2009[J]. Physica A: Statistical Mechanics and its Applications, 2012, 391(21): 5139-5145.

[3] MANDELBROT B. The Pareto-Levy law and the distribution of income[J]. Int Econ Rev, 1960, 1: 79-106.

[4] AYOAMA H, FUJIWARA Y, SOUMA W. Kinematics and dynamics of Pareto–Zipf’s law and Gibrat’s law[J]. Physica A, 2004, 344: 117-21.

[5] CHATTERJEE A, CHAKRABARTI B K, MANNA S S. Pareto law in a kinetic model of market with random saving propensity[J]. Physica A, 2004, 335: 155-63.

[6] FIGUEIRA F C, MOURA N J, RIBEIRO M B. The Gompertz-Pareto income distribution[J]. Physica A, 2011, 390: 689-98.

[7] XU Y, GUO L, DING N, WANG Y. Evidence of scaling in Chinese income distribution[J]. Chinese Physics Letters, 2010, 27(7): 078901.

[8] KMIETOWICZ Z W, DING H. Statistical analysis of income distribution in the Jiangsu province of China[J]. The Statistician, 1993, 42(2): 107-121.

[9] COWELL F A, VICTORIA-FESER M P. Robustness properties of inequality measures[J]. Econometrica: Journal of the Econometric Society, 1996, 64(1): 77-101.

[10] WU X, PERLOFF J M. China's income distribution over time: Reasons for rising inequality[J]. Cudare Working Paper, 2004(11611): 763-775.

[11] HAJARGASHT G, GRIFFITHS W E. Pareto–lognormal distributions: Inequality, poverty, and estimation from grouped income data[J]. Economic Modelling, 2013, 33: 593-604.

[12] GIBRAT R. Les Inégalités économiques[M]. Paris, France: [s.n.], 1931.

[13] CHAMPERNOWNE D. A model of Income distribution[J]. Economic Journal, 1953, 63: 318-351.

[14] RUTHERFORD R. Income distribution: a new model[J]. Econometrica, 1955, 23: 277-294.

[15] MONTROLL E W, SHLESINGER M F. On 1/noise and other distributions with long tails[J]. Proceedings of the National Academy of Sciences, 1982: 79(10): 3380-3383.

[16] STANLEY M H R, AMARAL L, BULDYREV S V, et al. Scaling behaviour in the growth of companies[J]. Nature, 1996, 379: 804-806.

[17] LEE Y. Universal features in the growth dynamics of complex organizations[J]. Phys Rev Lett, 1998, 81: 3275-3278.

[18] GABAIX X. Zipf's law for cities: an explanation[J]. The Quarterly Journal of Economics, 1999, 114(3): 739-767.

[19] REED W J, JORGENSEN M. The double Pareto- lognormal distribution-a new parametric model for size distributions[J]. Communications in Statistics Theory and Methods, 2004, 33: 1733-1753.

[20] KERM P V. What lies behind income mobility? Reranking and distributional change in Belgium, Western Germany and the USA[J]. Economica, 2004, 71: 223-239.

[21] COWELL F A, VICTORIA-FESER M. Robustness properties of inequality measures[J]. Econometrica, 1996, 64(1): 77-101.

[22] CLAUSET A, SHALIZI C R, NEWMAN M E J. Power-law distributions in empirical data[J]．SIAM Review, 2009(4): 661-703．

[23] SARABIA J M, FAUSTINO P, CARMEN T, et al, About the modified Gaussian family of income distributions with applications to individual incomes[J]. Physica A, 2013, 392: 1398-1408.

[24] JIN H. Income distribution in urban China: an overlooked data inconsistency issue[J]. China Economic Review, 2014, 30: 383-396.

[25] WEI C. Capital income and income inequality: Evidence from urban China[J]. Journal of Comparative Economics, 2012, 40: 228-239.

[26] LEE J. A provincial perspective on income inequality in urban china and the role of property and business income[J]. China Economic Review, 2013, 26: 140-150.

[27] SONG Z., STORESLETTEN K, ZILIBOTTI F. Growing like China[J]. American Economic Review, 2011, 101: 196-233.

[28] BACH S, CORNEO G, STEINER V. From bottom to top: the entire distribution of market income in germany, 1992–2003[J]. Review of Income & Wealth, 2009, 55(2): 303-330.

[29] 刘捷. 关于我国先富群体消费的理论思考[J]. 北京大学学报(哲学社会科学版), 2000, 37(1): 46-51.

LIU Jie. Theoretical reflection on the consumption of China' s get-rich-first group[J]. Journal Of Peking University (Humanities and Social Sciences), 2000, 37(1): 46-51.

[30] ROBERT L, YITZHAKI S. Income inequality effects by income source. a new approach and applications to the United States[J]. The Review of Economics and Statistics, 1985, 67(1): 151-156.

[31] Eguiluz V M, Zimmermann M G. Transmission of information and herd behavior: an application to financial markets[J]. Physical Review Letters, 2000, 85(26): 5659.

[32] Xie Y B, Wang B H, Hu B, et al. Power law distribution of wealth in population based on a modified Equiluz- Zimmermann model[J]. Physical Review E, 2005, 71(4): 046135.

[33] 孙文凯, 肖耿, 杨秀科. 资本回报率对投资率的影响:中美日对比研究[J]. 世界经济, 2010, 6: 3-24.

SUN Wen-kai, XIAO Geng, YANG Xiu-ke, The impact of capital rate of return on investment: the comparative study of American and Japanese[J]. The Journal of World Economy, 2010, 6: 3-24.

[34] FUJIWARA Y, SOUMA W, AOYAMA H, et al. Growth and fluctuations of personal income[J]. Physica A , 2003, 321(3-4): 598-604.

编 辑 蒋 晓

Variation Process of Chinese Income Distribution and Its Mechanism Analysis

XU Yan and WANG You-gui

(1. School of Economics and Management, North China University of Technology Shijingshan Beijing 100144; 2. School of Systems Science, Beijing Normal University Haidian Beijing 100875)

Power law distribution has been found in China with income data from 1998 to 2002 previously. With data from China Household Income Projects taken in 1988 and 1995, the distribution’s evolution procedure before power-law is studied, and power-law distribution is identified occurred in the late 90s. Economical analysis reveals a fact that the major changes of residuals income during this period are the emergence of Capital income. Accordingly, Gibrat’s model is modified by assuming a proportion of agents whose income changes with the features of capital income. Simulation results present two-segmental lognormal distribution in short term and power-law distribution in long term. It verifies that capital income is a main element to cause the variation of Chinese income distribution.

distribution variation process; Gibrat’s model; personal income; power-law distribution

O231.5

A

10.3969/j.issn.1001-0548.2016.05.023

2015-08-07；

2015-12-27

国家自然科学基金(61174165)；北京市组织部优秀人才项目(2013D005002000006)

许研(1983-)，女，博士，主要从事社会经济系统复杂性方面的研究.