异常链路分析在电力网络恢复中的应用

郭婷婷，赵承业



异常链路分析在电力网络恢复中的应用

郭婷婷，赵承业

(中国计量大学理学院 杭州 310018)

在大规模瘫痪状态下的电力系统的恢复过程中，网络中的一些特殊连边起到了关键作用，这是该文提出的基于异常链路分析的网络重构策略的主要思想。通过链路预测算法对网络中真实存在的连边进行异常度排名，以优先恢复异常度高的电源节点为目标，建立骨架网络恢复策略，然后根据链路的重要性进行骨架网络之外的线路的修复。这样不仅可以快速连通电源发电机，也能及时恢复重要线路，具有实际意义。

异常度; 异常链路; 链路预测; 网络重构; 恢复策略; 骨架网络;

各地的电力系统是一个庞大的网络，随着经济、社会的发展，人们对电力的依赖越来越强，电力系统所承受的压力越来越大，电力部门面对大规模停电的威胁也越来越显著，因此“黑启动”[1]方案受各国科研人员的关注度越来越高。所谓黑启动方案，是指整个系统因故障停运后，系统全部停电(不排除孤立小电网仍维持运行)，处于全“黑”状态，不依赖别的网络帮助，通过系统中具有自启动能力的发电机组启动，带动无自启动能力的发电机组，逐渐扩大系统恢复范围，最终实现整个系统的恢复。

电力系统在黑启动过程中分为3个阶段：1) 黑启动阶段；2) 系统重构阶段——主要目的是尽快给失电场站送电并建立一个骨架网络，为下一阶段全面恢复负荷(拥有发电机组的场站在网络中被标记为电源节点，除电源节点外，网络中的其他机组都可被看作是广义的负荷节点)打下基础；3) 负荷恢复阶段。大规模停电后网络重构阶段的主要任务是尽快给失电场站送电，快速恢复失电机组，并建立一个稳定的网架结构。在系统重构过程中要选择电源、负荷和线路的理想组合构成骨架网络。

为实现网络重构，一些学者根据网络中节点和连边的性质构造出了骨架网络，提出了网络恢复策略。文献[2]采用节点收缩后的网络凝聚度定义节点重要度，以网络重构效率(网络节点的平均重要度/网络的聚类系数)作为衡量重构效果的评价指标，提出了基于节点重要度评价的骨架网络重构策略，但未考虑到不同线路的相对重要性。随后，文献[3]在此基础上考虑线路介数，以节点重要度和线路介数作为重构指标，优先将重要节点和关键线路选入重构目标骨架网，从而为整个电网的全面、快速恢复奠定基础。文献[4]基于节点的恢复可靠性确定节点恢复序列，然后优先恢复待恢复节点中可靠性最高的节点，以此来提高系统恢复的成功率。文献[5]研究了节点间的供电关系，提出了一种基于后悔思想的节点重要度评价方法，但该方法在优化恢复路径时仅考虑了对重要节点的恢复。

考虑到实际网络中一些重要节点和连边的优先恢复，本文以链路预测算法为背景，考虑在网络中起重要作用的异常边，提出了基于异常链路分析的骨架网络重构方案。

1 异常链路分析

1.1 链路预测

每个网络都可以抽象成一个由节点集和边集组成的图，在记录网络的过程中，由于信息的不完全性，观测网络中会有链路的缺失问题，如信息的丢失及信息的刻意隐藏问题。

网络中的链路预测就是通过已知的网络节点以及网络结构等信息来预测网络中尚未产生连边的两个节点之间产生连接的可能性。这种预测既包含对未知链接(实际存在但未被探测到的链路)的预测，也包含对未来链接(目前不存在但应该存在或未来很可能存在的链路)的预测。链路预测将网络与信息科学联系起来，处理信息科学中缺失信息的还原和预测。学者们将节点间的相似性，即两节点间存在链接的可能性大小，直接用来进行链路预测。基于局部结构信息的相似性指标有典型的CN[6]、AA[7]、RA[8]等，基于路径的相似性指标有典型的Katz[9]、LP[8,10]等。衡量链路预测算法精确度的指标[11]主要有AUC、精确度(precision)和排序分(ranking score)，其中AUC[12]是最常用的评价指标，可以从整体上衡量算法的精确度；而排序分[13]更多考虑了所预测边的排序。

上述5种相似性指标的具体定义方法如下：

1) CN指标(common neighbors)：

2) AA指标(adamic-adar)：

3) RA指标(resource allocation)：

这是文献[8]中提出的资源分配指标，该指标考虑的是未直接相连的两个节点和之间的资源传递过程，其思路是将两节点间的共同邻居作为资源传递的媒介且这个媒介的单位资源平均传送给它的邻居，然后将节点可以接受到的传递的资源数定义为两节点间的相似性。

4) LP指标(local path)：

这是文献[10]在共同邻居基础上考虑三阶路径的因素提出的局部路径相似性指标，其中为可调参数，为网络的邻接矩阵，表示节点和之间长度为3的路径数目。

5) Katz指标

将局部路径指标扩展到无穷阶路径就得到全局路径指标：

1.2 异常边

针对网络中还未连接的节点对，上述链路预测算法(相似性指标)可以用来预测两节点间存在连边的可能性；针对网络中已经存在链接的节点对，如果通过相似性算法计算出这条边的相似度较低，说明它的存在在该网络中起到一定的重要作用。从这个角度上讲，链路预测算法可以用来评价链接存在的可信度或重要性。

所谓异常边[13]就是指网络中真实存在但是通过链路预测方法认为其存在概率很低的边。文献[13]中已有实验证明，异常链路对保持网络的连通性有特别重要的贡献，通过异常链路分析的方法能够有效地识别对网络连通性起重要作用的边。因此可以相信，优先恢复网络中的异常边对网络的恢复过程有重要指导意义。

对于链路预测算法，系统排序分值越小说明算法的预测效果越好；而对于异常边，排序分值越大说明链路越异常。

2 基于异常度的网络重构

2.1 重构思想

电力网络重构的目标是在网络大规模瘫痪的状态下，带电的发电机组以最短的路径对待恢复机组按其异常度确定优先次序进行供电，从而重建系统网架，加速系统恢复进程；然后以链路异常度作为标准依次恢复已恢复机组周围的待恢复线路。

电网具有复杂网络的某些共性，因此可以应用复杂网络中的链路预测方法作为筛选重要节点和关键线路的重构指标，为确定重构网络提供指导。将链路预测算法应用到电力系统的骨架网络重构上，实质是要在大规模停电后通过某种链路预测方法计算实际发电机电源节点的恢复次序并实现网络中所有失电机组的供电，为下一步的路径恢复奠定基础。文献[13]讨论了异常边对网络连通性的影响，指出异常链接分析的方法比边介数的方法更能够有效识别对网络连通性起重要作用的边。因此，通过预测精度较高的链路预测算法得到每条边的排序分，即异常度，然后计算所有待恢复电源节点的异常度，优先恢复图中异常度较高的电源节点。在电源节点的恢复顺序被确定后，采用改进的Dijkstra算法计算待恢复电源节点到其他带电电源节点的最短路径，由此可得到连通的电源节点骨架图；骨架网络重构完成后，按边的异常度从高到低依次恢复发电机电源周围的路径，从而实现整个网络的恢复。

由于重构过程中涉及诸多的技术性因素以及不确定性因素，在满足运行质量的前提下，依据网络结构进行网络的重构指导。考虑异常边及异常节点对网络的重要性，重构网络中所含异常边及异常节点越多说明重构方法越有效，因此本文定义重构网络效率为：

为达到高效的重构策略，需要以相对较少的线路将所有电源节点和异常度较高的负荷节点联系起来组成骨架网络，进而更好地指导整个网络的恢复过程。

2.2 算法描述

2) 选取预测精度值(排序分)最高的链路预测算法 (LPA)，计算每条边的异常度，进而确定电源节点的优先恢复次序：

BEGIN

FOR= 1 : 5

计算 RS；

END FOR

LPA= LPAs.t.RS=min{RS}；

RS= LPA[ train,]；

计算 RS；

Ranking(descend) {RS}；

END

//得到排序后的电源节点

3) 用改进的Dijkstra算法计算最短路径，保证优先、快速地恢复重要节点，得到电源节点构成的重构骨架网络：

BEGIN

FOR=1:(排序后的电源节点标号)

=1:

path(,) = dijkstra(,,);

END IF

END FOR

END

//得到按依序恢复电源节点的最短路径

4) 将已恢复机组周围的未恢复路线按其异常度从高到低进行恢复。

3 实例仿真

3.1 标准测试网试验

为验证本文方法的有效性及具体实现过程，选择IEEE30节点系统(30个节点，41条边)进行测试。排序分作为衡量链路预测算法精确度的指标，系统的排序分值越小说明算法的预测精度越高。而节点和边的排序分，即异常度，揭示了它们的重要性，排序分值越大则表示该节点和连边越异常，说明它们的重要性越大。通过上述理论，本文以IEEE30节点系统图(图1所示)为例，选取预测精度较高的链路预测算法来实现该系统的骨架重构。其中，衡量链路预测算法精确度的指标为排序分(ranking score)。

1) 逐项遍历IEEE30节点系统图中所有连边，将不同链路预测算法在该系统网络中的预测精度值记录在表1中。

表1 不同预测算法在IEEE30中的预测精度

由上述表格可知，RA指标得到的系统排序分最小，说明该指标对该系统网络的预测效果较好。

2) 通过RA指标来计算网络中连边的异常度，即排序分值，如表2所示。然后通过式(10)求得电源节点的异常度，确定所有发电机组的恢复次序。

表2 各线路的异常度

在图1中，方形节点代表发电机组(即电源节点)，其中节点1为可自启动发电机组，在系统瘫痪状态下可以自行启动，带动其他发电机组进行供电。由于发电机2与自启动发电机相关联，所以可以直接恢复；这5个发电机机组的恢复次序可通过表3中的异常度排名得到：2-23-13-22-27。

表3 电源节点的异常度

3) 根据确定的发电机组(电源节点)的恢复顺序，通过改进的Dijkstra算法得到最短恢复路径，包含11个节点和10条线路，如表4所示，也就是系统的骨架网络，如图1中虚线路径所示。

表4 IEEE30节点系统骨架网络重构策略

根据重构效率的定义，可计算得到该重构策略的效率值为：

对同一系统，文献[2]中得到的含6个负荷节点、13条线路的骨架网络效率值为1.172 4，文献[4]中得到的含6个负荷节点、11条线路的骨架网络效率值为1.117 8，由此可见本文方法可得到目前为止含最少路径数且重构效率较高的系统骨架。在现实生活中，快速得到骨架网络对指导整个网络的恢复工作有很大的实际意义。

4) 图1中各线路的权重值是其得分排名，骨架网络构造后，各发电机组(即电源节点)均已连通，可单独向未恢复的邻居机组进行供电。在各已恢复机组周围的未恢复线路中工作人员可依据其得分排名从高到低进行恢复。由于各电源节点均可独立工作，以节点22为例，当其恢复发电后，工作人员首先恢复线路(22,21)，而与节点27相关联的线路中(27,28)会被首先恢复；以此扩展，直到整个网络中的线路均恢复正常工作。

3.2 大规模网络试验

为进一步验证该算法在大规模真实网络中的有效性，本文以华中500 kV电网[14]为研究系统，计算该网络在大规模崩溃后指导重构的骨架网络。经过网络等值后，该网络共有136个节点(包含1个自启动电源节点，42个带有发电机组的电源节点)和175条连边。

首先通过各链路预测方法的预测精确度比较，选择在该网络中表现力较好的RA算法。通过该算法可得到各电源节点的异常度，并可根据其异常度得到重构网络中电源节点的恢复次序。

其中假设64号节点为自启动电源节点，所以无需恢复，而系统中也无与该节点直接相连的电源节点，所以可直接根据表5中电源节点的顺序进行恢复，对于异常度相同的节点按其编号进行排序，从而得到了电源节点的恢复次序，将这些节点按其排名顺序进行标号，然后通过2.2节中改进的Dijkstra算法计算骨架网络中的最短路径，可得到包含43个电源节点、56个负荷节点以及连接这些节点的102条路径的骨架网络系统，经过计算可得到该重构网络效率值为2.128 4。通过重构网络效率值的对比发现，基于异常度的重构策略在较大规模网络中同样有效。

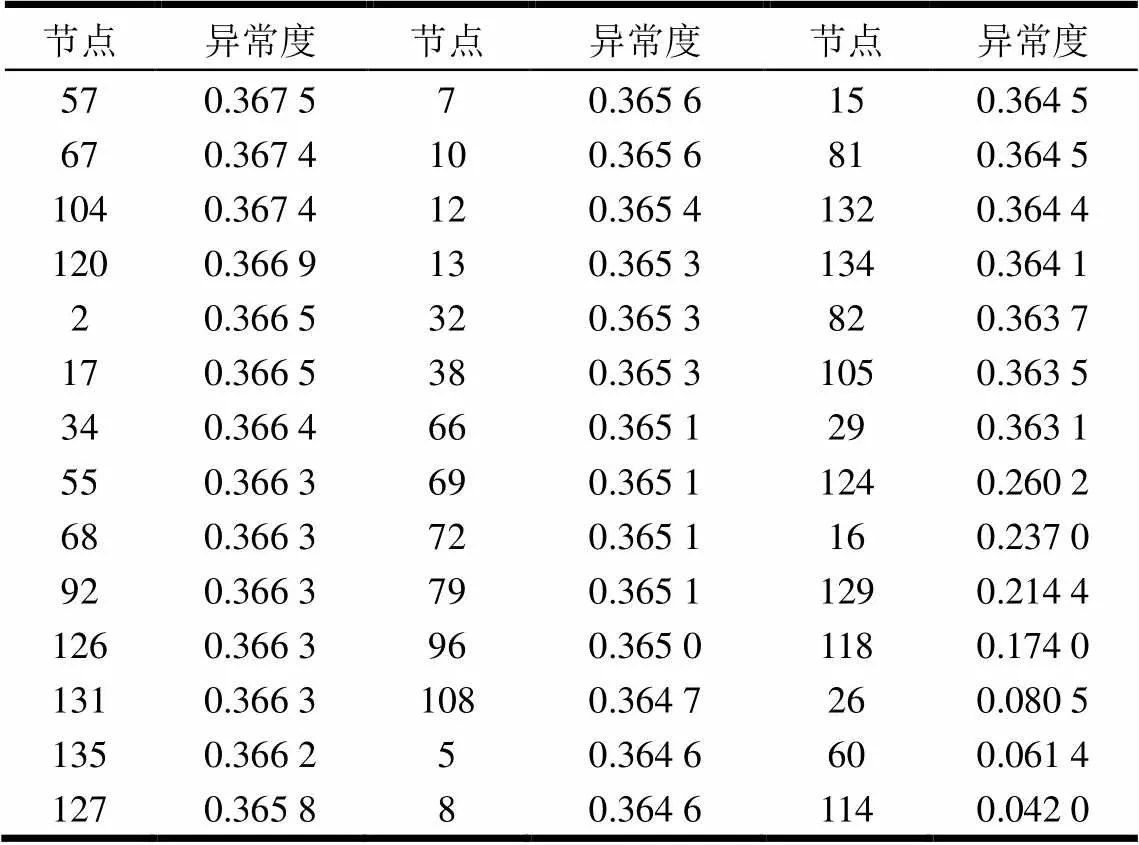
表5 各电源节点的异常度

4 结束语

本文在链路预测算法的基础上，通过异常链路分析的手段提出了一种电力骨架网络恢复策略，主要依据是链路预测得到的异常边刻画了这条边在该网络中的重要性。通过异常度确定电源节点优先恢复顺序，然后用最短路径算法快速构成骨架网络，为恢复整个网络奠定基础。在此基础上，再将网络中的重要链路及时修复，加快整个网络的连通，在实际应用中有重要意义。

参 考 文 献

[1] 周孝信, 郑健超, 沈国荣, 等. 从美加东北部电网大面积停电事故中吸取教训[J]. 电网技术, 2003, 27(9): 1.

ZHOU Xiao-xin, ZHENG Jian-chao, SHEN Guo-rong, et al. Draw lessons from large scope blackout of interconnected North America power grid[J]. Power System Technology，2003, 27(9): 1.

[2] 刘艳, 顾雪平. 基于节点重要度评价的骨架网络重构[J]. 中国电机工程学报, 2007, 27(10): 20-27.

LIU Yan, GU Xue-ping. Node importance assessment based skeleton-network reconfiguration[J]. Proceedings of the CSEE, 2007, 27(10): 20-27.

[3] 王亮, 刘艳, 顾雪平, 等. 综合考虑节点重要度和线路介数的网络重构[J]. 电力系统自动化, 2010, 34(12): 29-33.

WANG Liang, LIU Yan, GU Xue-ping, et al. Skeleton- network reconfiguration based on node importance and line betweenness[J]. Automation of Electric Power Systems, 2010, 34(12): 29-33.

[4] 梁海平, 顾雪平. 基于节点恢复可靠性的骨架网络重构[J]. 华北电力大学学报, 2014, 41(4): 30-34.

LIANG Hai-ping, GU Xue-ping. Skeleton-network reconfiguration based on node restoration reliability[J]. Journal of North China Electric Power University, 2014, 41(4): 30-34.

[5] 张璨, 林振智, 文福拴, 等. 基于后悔思想的网络重构两步策略[J]. 电力系统自动化, 2013, 37(8): 46-52.

ZHANG Can, LIN Zhen-zhi, WEN Fu-shuan, et al. A two-stage strategy for network reconfiguration based on the concept of regret[J]. Automation of Electric Power Systems, 2013, 37(8): 46-52.

[6] LORRAIN F, WHITE H C. Structural equivalence of individuals in social networks[J]. The Journal of Mathematics Sociology, 1971, 1(1): 49-80.

[7] ADAMIC L A, ADAR E. Friends and neighbors on the web[J]. Social Networks, 2003, 25(3): 211-230.

[8] ZHOU Tao, LÜ Lin-yuan, ZHANG Yi-cheng. Predicting missing links via local information[J]. Eur Phys J B, 2009, 71: 623.

[9] KATZ L. A new status index derived from sociometric index[J]. Psychometrika, 1953, 18(2): 39-43.

[10] LÜ Lin-yuan, JIN C H, ZHOU Tao. Similarity index based on local paths for link prediction of complex networks[J]. Physical Review E, 2009, 80(4): 046122.

[11] 吕琳媛. 复杂网络链路预测[J]. 电子科技大学学报, 2010, 39(5): 651-661.

LÜ Lin-yuan. Link prediction on complex networks[J]. Journal of University of Electronic Science and Technology of China, 2010, 39(5): 651-661.

[12] HANLEY J A, MCNEIL B J. The meaning and use of the area under a receiver operating characteristic (ROC) curve[J]. Radiology, 1982, 143: 29-36.

[13] 吕琳媛, 周涛. 链路预测[M]. 北京: 高等教育出版社, 2013.

LÜ Lin-yuan, ZHOU Tao. Link prediction[M]. Beijing: Higher Education Press, 2013.

[14] 王凯. 基于复杂网络理论的电网结构复杂性和脆弱性研究[D]. 湖北: 华中科技大学, 2011.

WANG Kai. Research on structural complexity and vulnerability of power grids based on complex network theory[D]. Hubei: Huazhong University of Science and Technology, 2011.

编 辑 蒋 晓

Application of Abnormal Links Analysis in Restoring Power Networks

GUO Ting-ting and ZHAO Cheng-ye

(College of Sciences, China Jiliang University Hangzhou 310018)

Some special links in the power system networks play a key role under the restoration process of large area breakout. This paper proposes a network reconfiguration strategy based on the analysis of the abnormal links. By ranking the abnormalities of these real links through link prediction algorithms, we establish a Skeleton-network recovery strategy, aiming at prioritizing restoring of nodes with high abnormalities, and then recover another links according to their significance. The strategy not only can connect the power generator quickly but also restore important routes timely, showing potential significance in practice.

abnormality; abnormal links; link prediction; reconfiguration strategy; recovery strategy; skeleton-network

TN711; O157.6

A

10.3969/j.issn.1001-0548.2016.05.024

2015-05-12；

2016-01-20

国家自然科学基金面上项目(61173002)；浙江省自然科学基金(LY14F020040)

郭婷婷(1991-)，女，主要从事复杂网络链路预测、图的连通支配集、无线网络分簇与骨干网构造方面的研究.