基于CUDA的SMAC算法并行化
2016-11-01常立博杜慧敏韩俊刚
常立博,杜慧敏,韩俊刚
(1.西安邮电大学 电子工程学院,陕西 西安 710121; 2.西安邮电大学 计算机学院,陕西 西安 710121)
基于CUDA的SMAC算法并行化
常立博1,杜慧敏1,韩俊刚2
(1.西安邮电大学 电子工程学院,陕西 西安 710121; 2.西安邮电大学 计算机学院,陕西 西安 710121)
改进SMAC(Simplified Marker and Cell)算法,增强其对流体模拟的实时处理能力。采用点差分格式对求解压力场和速度更新的偏微分方程进行离散化;引入消除数据相关性的存储算法以减少数据传输,并借助分层存储机制提高访存比,采用并行归约增加线程并行度;在统一计算设备架构平台下,对离散化的SMAC算法进行改进、优化及并行化实现。纯粹计算及多次迭代模拟实验结果显示,改进算法提速明显,可实现对一般场景的实时模拟。
计算流体力学;统一计算设备架构;并行算法
流体流动现象的模拟不仅是计算机动画、游戏、影视和飞行模拟等领域不可或缺的元素,也是科学计算可视化领域的研究热点之一[1]。常用的流体模拟算法有基于Stable Fluids[2]和基于SMAC[3]两类。Stable Fluids算法虽然可以较好地完成一般场景的模拟工作,但其本身存在严重的数值耗散,从而失去了模拟的物理真实感[1]。SMAC是MAC(Maker and Cell)方法的一种改进,具有良好的数值特性、求解精度和计算效率,已广泛应用于计算机图形学领域[4]。但基于SMAC的流体模拟算法存在复杂度较高、计算耗时过长等问题,无法用于实时性要求较高的场合。以提高计算密集型算法速度而发展起来的图形处理器(Graphic Processing Unit, GPU),为提高计算机动画实时模拟速度提供了新的解决方法,尤其是统一计算设备架构(Compute Unified Device Architecture, CUDA)平台的推出,进一步发挥了GPU的数据级并行计算能力,其强大的并行计算能力和浮点运算能力,以及可编程能力使得流体模拟加速成为可能。
文献[5]利用CUDA提供的库函数实现流体模拟的方法,模拟结果质量较好,但具体的实现原理并没有说明;针对求解偏微分方程的迭代算法的并行化设计方法,采用GPU实现了算法加速,虽然最高已达到9倍的加速,但依然不能满足实时流体模拟的需求[6]。文献[7]通过对SMAC算法离散化过程进行分析,为该算法并行化提供了理论依据,基于OpenGL和Cg语言在NV40显卡上得以实现,但限于当时的软硬件条件,很多步骤并没有在GPU上执行,导致加速比都不是很高,无法达到实时处理的要求。
本文拟采用点差分方法完成SMAC算法的离散化操作,讨论该算法在CUDA平台上实现时的数据存储算法、数据访存机制及线程分配,采用并行SMAC算法实现流体实时模拟。
1 SMAC算法原理及CUDA平台概述
1.1SMAC算法原理
流体模拟的基本方程N-S方程[8]采用交错网格离散化整个求解域。二维N-S方程的无量纲表达式为[7]
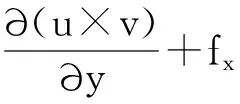
(1)

(2)

(3)
其中,x和y分别表示流场的横坐标和纵坐标,p表示压力值,fx和fy分别表示流场在x和y方向受到的外力,u和v分别表示在x和y方向的流场速度,Re表示雷诺系数。
针对每个模拟节点,令中间变量F和G表示为
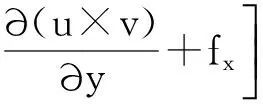
(4)

(5)
其中δt表示时间步进长度,n为模拟的迭代步数,将式(4)和式(5)分别代入式(1)和式(2),可得到

(6)

(7)
为保证速度场满足无源条件,引入压力投影映像来修正速度场,将式(6)和式(7)代入式(3),得到压力项的求解方程为

(8)
显式求解SMAC算法必须满足式柯朗-弗里德里希斯-列维(Courant-Friedrichs-Lewy Condition,CFL)条件[9],即最大速度值满足

(9)
|umax|δt<δx,|vmax|δt<δy。
(10)
其中δx和δy分别表示x和y的步进长度,umax和vmax分别表示速度场在x和y方向的极大值。所以,在流场中计算更新仿真步长,其核心是找到速度场中的极大值。
1.2CUDA并行设计架构
CUDA将GPU视为一个并行数据计算的设备,对所进行的计算进行分配和管理。CUDA主要有线程执行模式和存储组织形式两个显著特点[10-11]。
(1)线程执行模式
CUDA采用单指令多线程(Single Instruction Multiple Threads, SIMT)的执行模式,即每个处理单元(Streaming Processor, SP)执行1个线程、多个SP组成1个流处理器簇(Streaming Multiprocessor, SM)。每个SM的SP单元以连续的32个线程(称为1个warp)为单位来创建、管理、切换和执行指令,调试器不检查指令流内的依赖性,所以1个线程块内的线程数最好是32的整数倍。
(2)存储组织形式
CUDA结构中存储单元可分为全局存储器、常数存储器、共享存储器和寄存器,如图1所示。所有线程都可读写1块相同的全局存储器和1个只供读取的常数存储器;每个线程块都拥有1个共享存储器,同一线程块内的所有线程可以读写本块内的共享存储;每个线程都有1个容量较小但速度快的私有寄存器。由于访问共享存储比访问全局存储快数百倍,所以针对同一个线程块内的线程之间的通信,应当尽可能地使用共享存储以减少数据访存延时。

图1 CUDA存储结构
2 SMAC算法改进
2.1SMAC算法离散化求解
采用点差分格式离散纯二次项及混合二次项[12],则速度场在x和y方向二阶偏导的具体差分格式可表示为
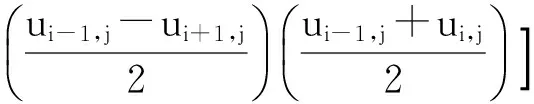
(11)
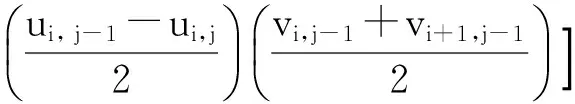
(12)
式中χ为人工粘性系数(χ=0.9)。
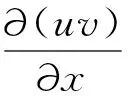

(13)
速度场主离散求解格式为
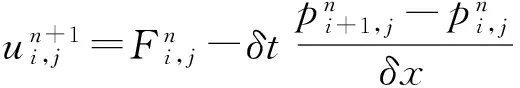
(14)

(15)
2.2SMAC算法并行实现步骤
根据SMAC离散化的过程,实现SMAC算法具体步骤如下。
步骤1初始化流场、边界条件和流场中障碍物分布。
步骤2初始化速度场和压力场。
步骤3计算每一个节点的F,G。
步骤4根据式(13)计算每一个节点的p。
步骤5根据式(14)和式(15)更新速度场。
步骤6根据式(9)和式(10)重新仿真步长。
步骤7根据压力场计算流场的密度场。
步骤8绘制密度。
如果速度场变化大于阈值或超过仿真时间则结束模拟过程,否则从步骤3开始下一次迭代。
可以看出,计算各节点的F,G和p参数只与相邻的4个节点和本节点的上一次迭代状态相关,而与以前的状态无关,具有时空局部性,可进行并行计算,从而减少计算时间,提高算法的运行速度。
3 基于CUDA加速的SMAC流体模拟
采用CPU和GPU协同的方式完成流体模拟。在CPU中设定流体的边界条件,将初始化场景数据传输到GPU存储中,并将每一格点上的计算任务分配给一个计算核上,当到达时间阈值时完成流体模拟计算;最后将模拟完成的场景数据传回CPU端,并利用图形渲染混合接口实现流体模拟的可视化操作,具体过程如图2所示。

图2 CUDA加速的SMAC流体模拟流程
3.1数据预处理
在建立场景时,对块间的ghost数据(边缘填充数据)进行预处理:在各块的四周用相邻块的数据进行填充,各块在计算之前,将填充好的ghost数据和本分块数据一同合并读入共享存储。中央块的ghost数据将由它周围的8个数据块中对应的数据组成。从而减少在模拟迭代过程中进行全局存储访问的操作次数。数据填充如图3所示。

图3 数据填充
假设流体模拟场景m×n,将其分解为T×T大小的块。原始场景用I(i,j)表示,变换后的场景用O(i,j) 表示,则流体模拟场景数据预处理过程可划分为两个主要部分,伪代码如下。
(1)对边界及ghost元素的处理
for (i=0;i<(m+2(m/T-1)+2);i++)
for (j=0;j<(n+2(n/T-1)+2);j++)
if(i==0)
O(i,j) =左边界;
else if(j==0)
O(i,j) =上边界;
else if(i==(m+2(m/T-1)+1))
O(i,j) =右边界;
else if(j==(n+2(n/T-1)+1))
O(i,j) =下边界;
else if(m%((i-1)*T)==0) {
if(n%((j-2)*T)==0)
O(i,j) = I(i-1,j+1);//右上角ghost元素
else if(n%(j-1)*T)==0)
O(i,j) = I(i-1,j-1); //左上角ghost元素
else
O(i,j)= I(i-1,j); //上边ghost元素
}
else if(m%((i-2)*T)==0) {
if(n%((j-2)*T)==0)
O(i,j) = I(i+1,j+1);//右下角ghost元素
else if(n%(j-1)*T)==0)
O(i,j) = I(i-1,j+1); //左下角ghost元素
else
O(i,j) = I(i+1,j); //下边ghost元素
}
else if(n%((j-1)*T)==0)
O(i,j) = I(i,j-1);//左边ghost元素
else if(n%((j-2)*T)==0)
O(i,j) = I(i,j+1);//右边ghost元素
(2)对真实场景数据的处理
for(k=0;k for(l=0;l for(j=0;j for(i=0;i O(k*T+j+1,l*T+i+1) =I(k*T+j,l*T+i); } 3.2数据传输单元设计 在场景初始化时将速度场、压力场和受力场由CPU传输到GPU,完成场景模拟之后再将速度场和压力场由GPU传输到CPU;而数据填充、对各节点的速度场和压力场计算及更新均在GPU端完成,从而减少数据在显存和主存中传输的次数。 3.3核心计算单元设计 为了避免同1个warp中出现分支,使用1个线程计算1个节点的F、G、p信息及速度更新操作,将16×16或32×32个线程组成1个线程块,并根据模拟场景自动确定线程块数量。如果要模拟的场景不规则,则在进行模拟之前先对场景进行无用数据填充,再进行场景模拟。 利用共享存储作为数据“中转站”以降低非合并访问。同时经过数据填充处理过的状态信息,块与块之间的信息是完全不相关的。利用CUDA提供的访存延时隐藏技术,即在处理过程中,先启动所有块对全局存储访问,再进行计算,这样几乎可以隐藏所有的访存延时。 3.4求解迭代步长单元设计 方程解随着时间步的递进而更新,直到计算时间溢出。设定空间步长为1,由式(10)确定各时间步之间的时间推进量。采用并行归约方法计算每一个时间步的速度最大值[12],具体如图4所示。假如对N个数据进行求极大值操作,开启N/2个线程分别进行两两比较大小,如0号线程求第0和第N/2+1个数据中的较大值,结果写入第0个数据的存储空间,同理可推其他线程计算的数据;每个循环参与计算的线程数减半,最后,0号单元的数据和1号单元的数据比较以计算出极大值,此算法将求极大值运算复杂度降为log2(n)。在实现过程中,首先在同一个线程块内完成速度场每行极大值的计算,然后将各线程块的极大值(即各行的极大值)放在0号线程块中计算出速度极大值。 图4 并行归约求极大值 为了验证改进后的SMAC算法在流体模拟中的有效性和效率,采用基于Intel i7 5500U的CPU、基于nVIDIA GTX560处理器的GPU和分别基于gcc 和nvcc3.0平台的编译器,分别完成了基于SMAC算法流体模拟的串行及并行实现。并且,对不同计算规模下的单次迭代及相同计算规模下多次迭代的性能进行了分析。 4.1单次迭代的性能分析 表1为模拟1个时间步长的运行时间分布,在不同计算规模下,CPU耗费的时间同GPU耗费的时间对比。其中GPU计算时间只包括GPU上由原始速度场u、v,力场fx、fy,初始压力场p计算得到1个时间步的速度场和压力场的时间,不包括GPU和CPU之间数据传输时间,即纯粹计算时间。 表1 单步长的加速时间分布 从表1可看出,当模拟的流场较大(1 024×1 024)时,采用CPU实现的串行计算方法每秒仅可完成约6次流体场景计算,无法实现实时流体场景模拟。然而,采用并行SMAC算法每秒仅可完成数百次对流体场景模拟计算,所以完全可实现实时流体场景模拟。 4.2多次迭代性能分析 表2为计算规模(512×512)一定时,不同迭代次数CPU的时间同GPU的时间对比。其中GPU计算时间表示GPU+CPU的计算总时间,包括将原始速度场u、v,力场fx、fy,初始压力场p由CPU传输到GPU,和将模拟后的速度场u、v、压力场p传输回CPU的传输时间,和在GPU上多次迭代的运算时间。CPU计算时间表示CPU串行模拟时间。 表2 多步长的加速时间分布 从表2可以看出,针对中等规模(512×512)的流体模拟场景,在场景不是十分复杂(即在迭代次数小于100时求解方程收敛)的情况下,采用GPU并行实现方法模拟速度可达到20~30 fps,基本可满足实时流体模拟的要求。 从实验结果可以看出,采用点差分离散方法对SMAC算法进行离散化,并采用数据填充算法及各种优化计算方面可以完成对一般流体场景进行实时模拟的工作。 采用点差分离散方法实现SMAC算法中求解压力场、速度更新等操作的并行化处理。然后,从减少数据传输、提高访存比及增加线程并行度等方面,对离散化的SMAC算法在CUDA平台下进行改进和优化。最后,将改进后的算法在CUDA架构下实现。实验结果表明,基于CUDA架构的SMAC并行算法提速效果明显,可实现对一般场景的实时模拟工作。 [1]佟志忠, 姜洪洲, 韩俊伟. GPU加速的二维流体实时流动仿真[J/OL]. 哈尔滨工程大学学报, 2008, 29(3):278-284[2015-12-22]. http://d.wanfangdata.com.cn/Periodical/hebgcdxxb200803015. DOI:1006-7043( 2008) 03-0278-07. [2]STAM J. Stable fluids[J/OL]. Acm Transactions on Graphics, 1999:121-128[2015-12-20]. http://www.dgp.toronto.edu/people/stam/reality/Research/pdf/ns.pdf. [3]AMSDEN A A, HARLOW F H. A Simplified MAC Technique for Incompressible Fluid Flow Calculations Physics[J/OL]. Journal of Computational , 1970, 6(2): 322-325[2015-12-20]. http://dx.doi.org/10.1016/0021-9991(70)90029-X. [4]张永学, 曹树良, 祝宝山. 求解不可压三维湍流的隐式SMAC方法[J/OL]. 清华大学学报(自然科学版), 2005, 45(11):1561-1564[2015-12-30]. http://dx.chinadoi.cn/10.3321/j.issn%3a1000-0054.2005.11.031. [5]KRAUS J, SCHLOTTKE M, ADINETZ A, et al. Accelerating a C++ CFD code with OpenACC[C/OL]// 2014 First Workshop on Accelerator Programming using Directives (WACCPD), New Orleans, LA:IEEE, 2014:47-54[2015-12-30]. http://dx.doi.org/10.1109/WACCPD.2014.11. [6]AMADOR G, GOMES A. CUDA-Based Linear Solvers for Stable Fluids[C/OL]// 2010 International Conference on Information Science and Applications (ICISA), Texas , LA:IEEE, 2010:1-8[2015-12-30]. http://dx.doi.org/10.1109/ICISA.2010.5480268. [7]SCHEIDEGGER C E, COMBA J L D, Da C R D. Practical CFD Simulations on Programmable Graphics Hardware using SMAC[J/OL]. Computer Graphics Forum, 2005, 24(24):715-728[2015-12-30]. http://dx.doi.org/10.1111/j.1467-8659.2005.00897.x. [8]CHORIN A J. Numerical Solution of the Navier-Stokes Equations*[J/OL]. Mathematics of Computation, 1968, 22(104):17-34 [2016-1-1]. http://dx.doi.org/10.1016/B978-0-12-174070-2.50005-8. [9]LAX P D, HERSH R, JELTSCHR, et al. The Courant-Friedrichs-Lewy (CFL) Condition[J/OL]. Communications on Pure & Applied Mathematics, 1962, 15(4):363-371[2016-1-1]. http://link.springer.com/978-0-8176-8394-8.DOI: 10.1007/978-0-8176-8394-8. [10]KIRK D B. Programming Massively Parallel Processors[M/OL].北京:清华大学出版社, 2010:24-46[2016-1-10]. http://www.doc88.com/p-2939593408781.html. [11]COOK S. CUDA Programming: A Developer’s Guide to Parallel Computing with GPUs[M/OL]. Morgan Kaufmann Publishers Inc., 2012:155[2016-1-10].http://download.csdn.net/detail/niexiao2008/5780159. [12]HIRSCH C.Numerical computation of internal and external flows [M/OL]. Butterworth-Heinemann, 2007:491-539[2016-1-10].http://dx.doi.org/10.1016/B978-075066594-0/50053-9. [13]李大力,张理论,徐传福,等. 雅可比迭代的CPU/GPU并行计算及在CFD中的应用[C/OL]// 2012全国高性能计算学术年文集.张家界:中国计算机学会,中国软件行业协会,2012:1-8[2016-1-10].http://www.ccf.org.cn/sites/ccf/gxnjs.jsp#8. [责任编辑:祝剑] SMAC algorithm parallelization based on CUDA CHANG Libo1,DU Huimin1,HAN Jungang2 (1. School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;2. School of Computer Science and Technology, Xi’an University of Posts and Telecommunications, Xi’an 710121, China) SMAC (Simplified Marker and Cell) algorithm is improved in order to enhance the ability of real time processing for fluid simulation. The algorithm is discretized for solving pressure field and update speed used by central difference scheme. A data storage algorithm that can eliminate data correlation is proposed to reduce data transmission. Usage of memory is optimized based on CUDA and the parallel computing threads into appropriate blocks is organized to make better use of stream multiprocessor in GPU. The discretization of the SMAC algorithm is improved, optimized and parallel implemented under the CUDA (unified computing device architecture) platform. Result show that GPU-based implementation of SMAC can achieve a significant speedup compared with CPU based counterpart both in the SMAC algorithm and in real simulation. Therefore the improved algorithm can achieve real-time simulation of the general scene. computational fluid dynamics, compute unified device architecture, parallel algorithm 10.13682/j.issn.2095-6533.2016.05.007 2016-03-14 国家自然科学基金资助项目(61136002);西安市科技发展计划资助项目(CXY1440(10)) 常立博(1985-),男,助教,硕士,从事计算机体系结构、高性能计算研究。E-mail: changlibo@xupt.edu.cn 杜慧敏(1967-),女,教授,博士,CCF会员。从事计算机体系结构、计算机图形学研究。E-mail: duhuimin0529@126.com TP338.6 A 2095-6533(2016)05-0033-06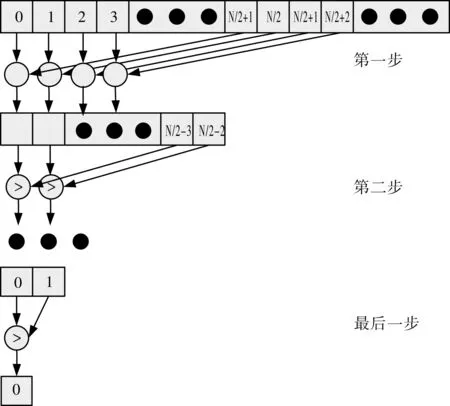
4 实验方法与结果分析


5 结语
