动车组牵引系统部件故障分布规律评估方法研究

李杰波

( 中国铁道科学研究院　机车车辆研究所， 北京 100081)



动车组牵引系统部件故障分布规律评估方法研究

李杰波

( 中国铁道科学研究院机车车辆研究所， 北京 100081)

基于可靠性理论和动车组牵引系统故障特点，对动车组牵引系统的故障分布规律的分析方法进行了探讨，阐述了用可靠性理论识别系统故障分布规律的模型。提出对动车组牵引系统故障样本极少的部件采用平均故障率描述，对故障规律不明显的部件采用经验分布函数方法，对多种故障模式相互作用部件采用理论分布估计，可以得到较为理想的部件寿命规律。

动车组； 可靠性； 故障分布

根据2011年京津城际CRH3C型动车组运营故障统计分析结果，牵引系统(包括高压子系统和牵引传动系统)故障数占动车组总故障数(牵引系统、网络、制动、转向架等系统)的32.3%[1]。牵引系统故障凸显为动车组运用的主要故障，牵引系统的可靠性直接影响了动车组的运行准点。

日本新干线检修充分考虑车辆各部件发生故障的概率确定检修周期；德国ICE列车和法国TGV列车已经不约而同地采用RCM理论和方法，最重要的是通过运用中对关键部件和系统的监测分析获得部件或子系统实际可靠性指标和潜在寿命，根据故障率变化规律决定维修方式，避免直接采用供货商给出的不准确的或过于保守的可靠性指标和寿命参数决定维修时机，并逐步开展修程优化工作，延长部件工作寿命。欧洲和日本的高速铁路已经运用可靠性理论逐步实行RCM维修制度、优化修程，可靠性工程深入地应用到了维修体制中[2]。

与国外动车组相比，我国动车组服役时间短，不仅缺乏准确的可靠性设计指标，并且由于运用条件的复杂性造成实际可靠性指标不匹配。因此，对于故障率较高的牵引系统，通过现场故障数据按照可靠性理论对其故障规律进行分析，以得到较为贴近实际的可靠性运用指标指导检修，意义重大。

1　动车组牵引系统现场故障数据分析方法

由于我国动车组的运用时间较短，收集到的牵引系统零部件故障信息仅表现出牵引系统前期的故障情况，因此可以通过借鉴其他行业零部件的寿命分布研究经验，对牵引系统中具有较明显寿命分布类型的零部件采用经典统计方法来确定分布模型，拟合成理论分布函数是首选方法。

此外，在找不到能充分反映数据特征的理论分布函数情况下，可以采用经验分析法(又称非参数法或自由分布法)，其目标是直接从故障时间序列推断出故障分布、可靠性函数和故障率函数。

分布假设方法首先应识别判断数据的分布类型，通过参数估计的方法给出表征可靠性指标的参数，最后对分布类型进行拟合优度检验。

(1)选择候选分布

可靠性工程中常用的分布有指数分布、威布尔分布、正态分布、对数正态分布等。一般识别候选分布有两种方法：

①直方图

直方图是一种将故障时间按级分类，然后画成以每级的频数或相对频率(频数/总数)相对于每级的时间组距的图形。

由样本数据计算得到的描述性统计量可用于识别候选分布或者排除一些分布。例如，如果故障时间服从一个对称或近似对称的分布，如正态分布或者形状参数在3～4之间的威布尔分布，那么样本均值和故障时间的中值大致相同。如果均值明显大于中值，也就是数据是右偏的，那么指数分布、对数分布或者威布尔分布将提供较好的拟合。如果故障数据服从指数分布，则样本均值和标准差大致相等。正态分布还可以通过偏锋度进行检验[3](偏度定义为Cs，峰度定义为Ce)。寿命分布分析流程如图1。

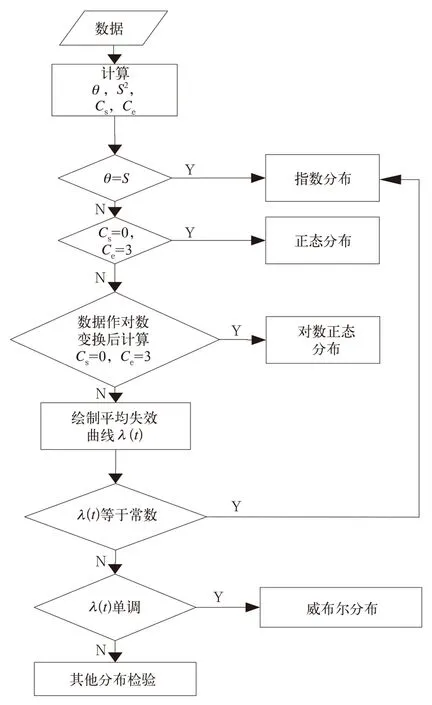
图1　寿命分布选择流程图

②概率图和最小二乘法曲线拟合

概率图提供一种通俗简便的方法来评估将数据拟合为一种分布的拟合程度，主要方法是将数据转换后拟合成一条线性回归(最小二乘法)线。利用图识最小二乘法优选分布类型[4]，需要对累计故障分布函数F(t)进行线性转换，如采用直线方程y=Bx+A，则不同分布的线性转换关系见表1。

(2)参数估计

参数估计是根据所获得的试验数据或者现场数据，利用数理统计方法来估计寿命分布中的未知参数；估计的精度取决于所选用的估计方法和样本的大小。

参数估计的方法包括概率图法、最小二乘法、极大似然估计等。如概率图法和最小二乘法可以结合相关系数和残差平方和综合分析确定最优分布，其判定原则是：残差平方和要小，相关系数应较大，残差图的正态性要好。

(3)拟合优度检验

拟合优度检验的一般步骤为：

①建立原假设H0：总体分布函数F(t)=F0(t)。

②构造一个反映总体分布与由样本所获得的分布之间的偏差的统计量D。

③根据样本观测值计算出统计量D的观测值d。

④规定检验水平α(一般取0.10，0.05，0.01等)，相应求得D的临界值d0，使：PD≥d0=α。

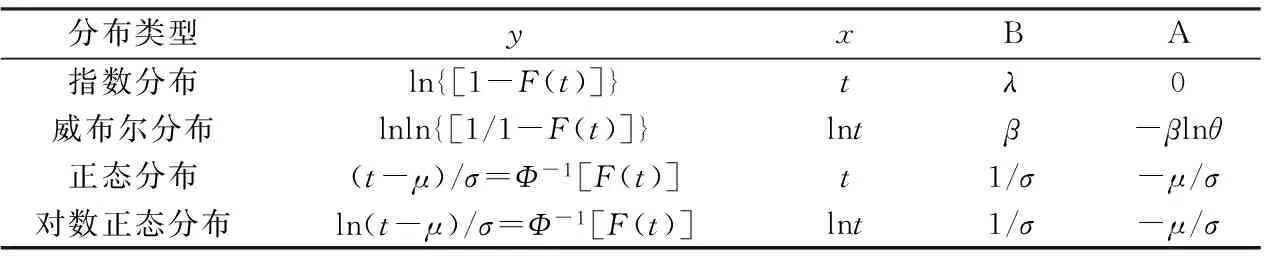
表1　不同分布对应概率图和最小二乘法的坐标线性转换关系

⑤比较d和d0的大小，当d>d0时拒绝假设H0；当d≤d0时接受假设H0。

常用的可靠性分布检验有卡方检验、K-S检验、F检验、偏锋度检验等，在功能上计算机程序已经完全可以取代人工计算。

2　动车组牵引系统部件寿命规律分析

牵引系统零部件的寿命分布规律，一部分部件可以采用先验分布(如文献已明确的分布类型)来简化评估过程，如有文献提出动车组高压电器系统除受电弓其余部件的寿命均服从指数分布[5]、电气系统的主要零部件的寿命均服从指数分布[6]、电机寿命服从指数分布等[7]，构造复杂并由多种故障模式独立作用的部件可以通过对故障数据的分布拟合获得。以某型动车组为例，表2为动车组近10年牵引系统部件故障数的统计，该型动车组单列平均运行里程218万km。

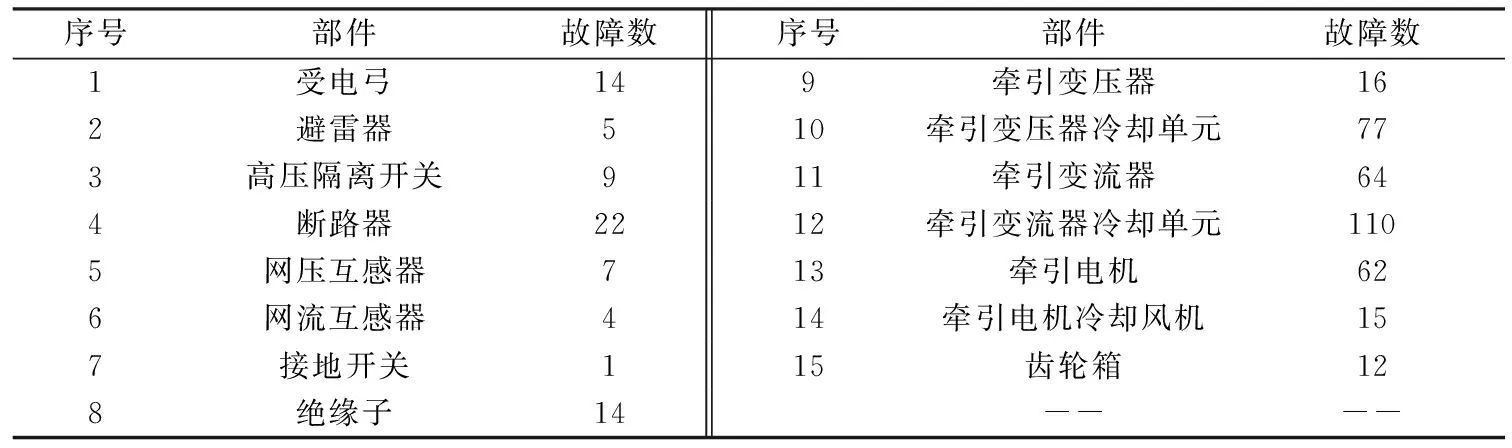
表2　牵引系统故障数

(1)首先，对故障率极低且表现为偶发故障形式的部件，如避雷器、高压隔离开关、高压互感器、接地开关、绝缘子、高压电缆、牵引变压器、牵引风机，可以认为服从指数分布以简化评估过程，计算其平均故障率。

(2)对故障规律不明显的部件采用经验分布函数方法

该型动车组在现场运用过程中受电弓早期故障率非常高，因此经过了一系列技术整改，受电弓完全改造后共计故障数为14次。受电弓上臂、风管、碳滑板以及连杆等故障次数较多，属于薄弱环节，基本上为机械磨损类型故障。改造后由于统计时间短，故障数据少，因此受电弓的故障规律并不明朗，宜采用经验分布函数方法对改造后的受电弓故障进行分析。计算结果见图2。从故障概率密度曲线观察，改造后的受电弓故障分布服从正态分布，较为符合磨损型部件的故障规律。

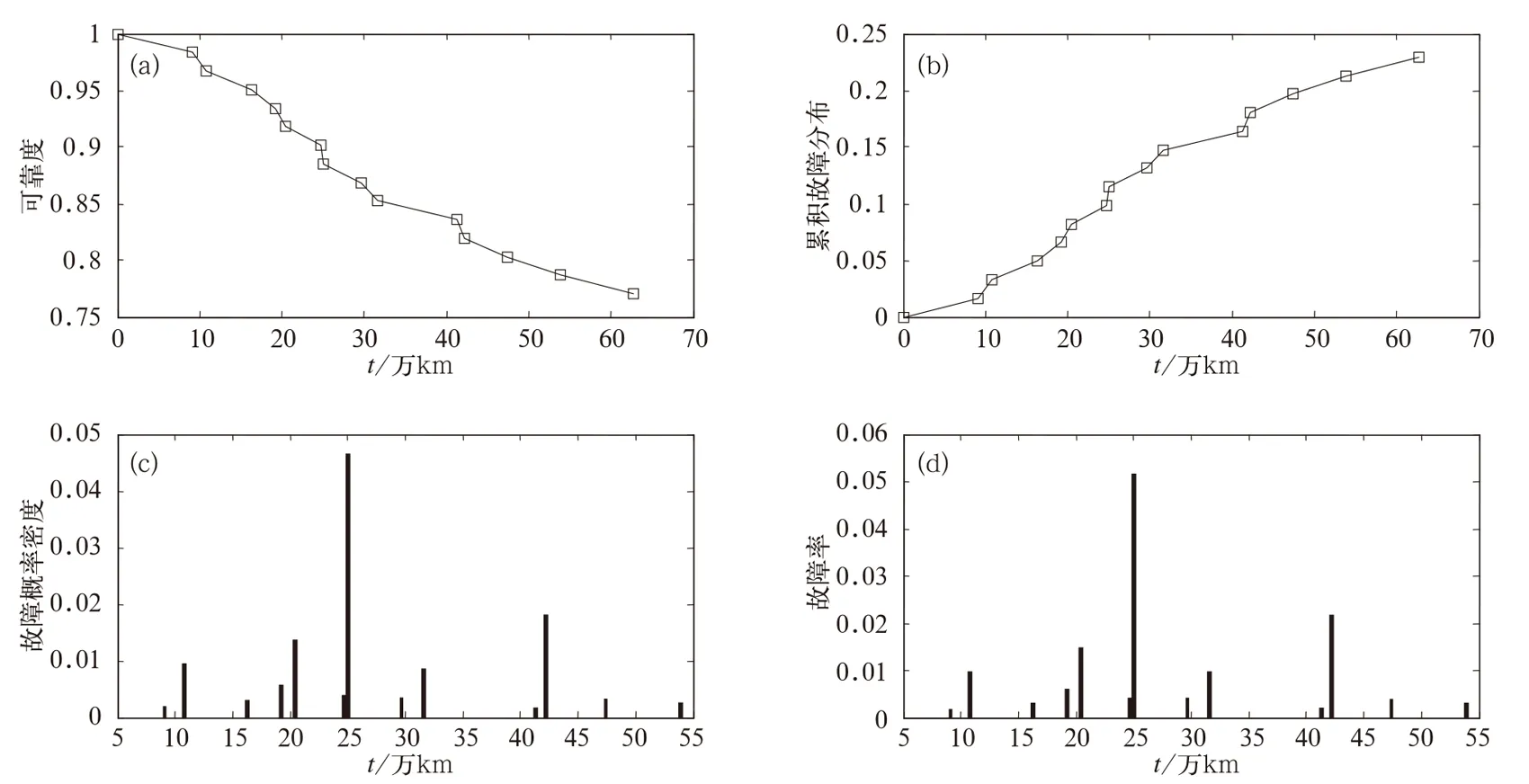
图2　改造后受电弓故障分布图

按照表1对累计故障分布函数F(t)进行线性转换后采用最小二乘法拟合，拟合相关系数为0.85。受电弓服从N(84.165，42.576)的正态分布，如图3所示。

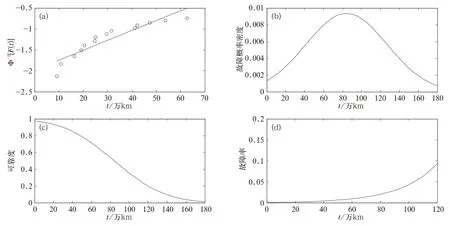
图3　改造后受电弓寿命分布规律

改造后的受电弓走行里程约20～60万km左右，经历的生命周期尚短，每列车改造时间、走行公里数存在差别，对改造后的受电弓寿命评估理论上会存在一定偏离，使得相关系数较低。

(3)对故障规律较明显部件采用理论分布估计

部分一级部件构造复杂并由多种故障模式独立作用，如牵引变流器、牵引电机、冷却系统等，既存在磨耗型故障，也存在电、热应力型故障，可以通过对故障数据的分布拟合获得其寿命规律。

以该型动车组牵引变流器冷却单元为例，牵引变流器冷却单元中由冷却风机、热交换机、温度传感器、压力传感器、滤网、膨胀水箱、管路、水泵、内部风扇、继电器等部件构成。其主要功能是为牵引变流器提供散热条件，保证牵引变流器工作在适宜的环境下。

将牵引变流器冷却单元相关故障信息统计结果汇总如表3所示，其中压力传感器故障次数最多，达到了38次；其次是热交换器故障发生次数。

表3　牵引变流器冷却单元故障信息统计表

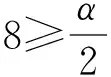
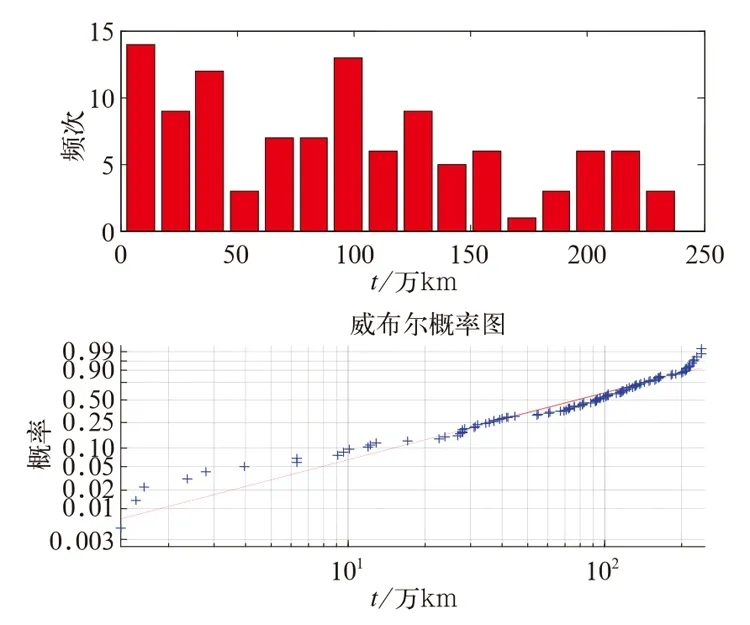
图4　牵引变流器冷却单元寿命分布规律

3　结　论

牵引系统故障对动车组运行影响较大，运用检修部门积累了所有现场运用故障数据，可以结合可靠性理论

采用适当的方法获得系统或部件的寿命规律。针对动车组牵引系统，提出对故障样本极少的部件采用平均故障率描述，对故障规律不明显的部件采用经验分布函数方法，对多种故障模式相互作用部件采用理论分布估计，可以较为理想地获得部件的寿命规律，为制定可靠性指标，进一步指导检修和优化修程修制提供依据。

[1]王彩霞. 高速动车组主要零部件损伤规律及维修周期的研究[D]. 北京: 北京交通大学, 2012.

[2]文强. 国内外高速列车检修制度综述[J]. 国外铁道车辆, 2014,(2): 1-3.

[3]赵宇. 可靠性数据分析[M]. 北京: 国防工业出版社, 2011.

[4]杜峰, 魏朗, 李伦. 整车产品故障分布规律与可靠性评价指标分析[J]. 农业机械学报, 2008, 39(1):172-175.

[5]刘建强,崔秀国,孙帮成,王贵国,等. CRH3C型动车组高压电器系统可靠性研究[J]. 铁道学报, 2013, 35(6):22-27.

[6]崔秀国. CRH3型动车组电气系统可靠性研究[D]. 北京：北京交通大学, 2013.

[7]刘佳昌,牛天福,罗恒森. 电机寿命分布的数学模型[J].哈尔滨电工学院学报, 1995,18(4):472-475.

Research on Failure Distribution Evaluation Method of Traction System Components for EMU

LIJiebo

(Locomotive & Car Research Institute, China Academy of Railway Sciences, Beijing 100081， China )

Based on the reliability theory and the fault characteristics of EMU traction system, the analysis method of the fault distribution of EMU traction system is discussed. The average failure rate is described, and the empirical distribution function is used to describe the failure of the components of the traction system.

EMU; reliability; failure distribution

1008-7842 (2016) 04-0081-04

��)男，副研究员(

2015-12-18)

U266.2

Adoi:10.3969/j.issn.1008-7842.2016.04.20

2015年铁道牵引动力学术年会论文