让策略和方法在“让学”中自然生成
2016-10-29吴存明
吴存明
【设计理念】
基于新课标提出的数学教学要“形成解决问题的一些基本策略”这一要求,苏教版教材编排了一个“解决问题的策略”单元,精选了画图、列举、假设、转化等常用策略。苏教版五下安排的“转化”策略是一种十分常见又极其重要的思想性策略,对于学生形成分析和解决问题的能力以及发展数学思考,具有非常重要的意义。
1.为什么修订版教材将“转化”策略提前到五年级来教学?
在2014版修订教材中,《解决问题的策略:转化》一课由原来的六下提前到了五下。为什么作这样的调整呢?在备课过程中,我翻阅了一到十册教材,心中有了答案。通过多年的学习,转化策略对五年级的学生来说已不是新鲜事物,他们早已接触并积累了较多通过转化解决问题的经验(如小数的乘除法转化为整数的乘除法、未知图形的面积转化为已知图形的面积等),及时安排转化策略的认识和应用,既可以帮助学生将感性经验提升为理性思考,也能为他们后续主动运用转化策略学习新的知识(如长方体、正方体、圆柱的体积等)提供强有力的支撑,还有利于进一步增强他们应用策略分析和解决问题的能力,使他们形成策略意识。
2.策略和方法哪个更重要?
目前,小学数学界普遍认为,相对于方法而言,策略属于上位知识,而本人认为,方法和策略是解决同一问题过程中的两个方面,在学习、掌握解决问题的某种方法时,也就逐步了解和形成了解决问题的策略。因此,在教学中,应注重探究方法,让学生不断观察、体验、反思、抽象和概括,使策略与方法这两者更紧密地联系起来。
3.选择哪些问题作为教学“转化”的素材?
例1选择了两个不规则图形转化为规则图形,有利于学生直观感知转化策略的优势,例2虽然是下一课时的内容,但为了学生对转化有更整体的认识,也可以将其纳入本节课的教学。于是,教学时,我选择将图形的等积转化(例1)、等长转化(“练习十六”第1题)、连加式题的等值转化(例2)等素材作为教学的核心问题,使学生通过回顾学习经历意识到转化是常用策略,从而主动应用转化策略解决问题。
总之,本设计紧紧围绕让数学课堂从“教为中心”转为“学为中心”的理念,依据教材设计了五个教学板块,以期让学生的学习自然发生。
【教学目标】
1.使学生初步学会运用转化的策略分析问题,并能根据问题的特点确定具体的转化方法,从而有效地解决问题。
2.使学生通过对解决问题的反思和对旧知的回顾,体会转化策略的价值。
3.使学生进一步积累解决问题的经验,增强主动应用策略解决问题的意识,获得成功解决问题的体验。
【教学活动及意图】
一、课前热身,渗透转化
师:同学们知道今天学什么吗?老师来试试大家的解题本领高不高。
问题:不给你大的秤,你怎么称出一头大象的质量?
预设:学生说出曹冲称象的办法,教师顺势播放动画短片《曹冲称象》。
师:曹冲聪明在哪里?(使用策略)
小结:接下来的40分钟,就让我们一起向曹冲学习,走进策略的世界,去领略策略的神奇,好吗?
【课前热身,调动学生学习的热情,激发学生学习的兴趣。此外,通过两个看似随意的问题,有效激活了学生的思维,并与本节课要学习的转化策略有效衔接,将学生的注意力集中到解决问题的策略上来。】
二、问题引入,感知转化
师:让我们的学习从聪聪和明明的争论开始!
1.核心问题1:谁的面积大?
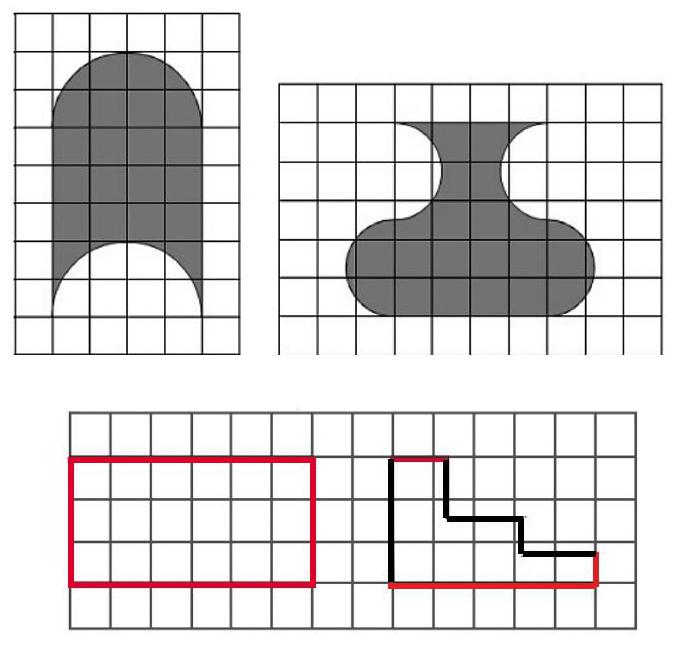
聪聪和明明在方格纸上分别画了一个图形,他们想知道究竟谁画的图形面积大,你们有办法吗?
预设:有的学生说一样大,有的学生说右边的图形面积大。
师:在老师给大家的白色信封里,拿出这两个图形,动手试试,验证自己的想法。
指名上台汇报。
追问:你的结论是什么?你觉得他说得怎么样?还有不同的方法吗?刚才大家的方法有什么共同点?
指出:其实,刚才大家在变形过程中,平移也好,旋转也好,都用到了一种解决问题的策略——转化。(板书课题)
追问:刚才,我们把什么转化成了什么?(不规则图形转化成了规则图形)转化前后,什么变了,什么没变?(形状变了,面积不变)
追问:不转化行不行?
根据学生的回答,课件相机展示数方格法和变形法,并引导他们比较:哪种方法好?(变形法方便,数方格法麻烦)
【尊重教材编写意图,从比较不规则图形的面积入手,唤醒学生的转化意识,容易想到转化成规则图形来比较。融入“聪聪和明明比赛”的情境,有利于学生投入思考。让学生充分表达自己的想法,尊重不同学生的认知起点。通过数方格法和变形法的鲜明对比,让学生初步感受转化策略的优势。】
过渡:比谁的面积大,他们打成了平手,他们又开始了第二次比拼!我们去看看!
2.核心问题2:谁的周长长?
聪聪和明明又在方格纸上分别画了一个图形,这一次他们想知道究竟谁画的图形周长长,有办法吗?
预设:有的学生说一样长,有的学生说右边的图形周长长。
指名上台汇报。师追问:还有不同的方法吗?
根据学生的回答,课件相机展示不同的转化方法,得出结论。
追问:刚才,我们是借助什么策略解决问题的?
小结:同学们已经能主动运用转化的策略解决问题了,真棒!
追问:这一次转化前后,什么变了,什么没变?(面积变了,周长不变)
指出:前面一次比谁的面积大,转化时面积不能变,叫作“等积变形”;这一次比谁的周长长,转化时周长不能变,叫作“等长变形”。总之,比什么量,转化前后,什么量就不能变,否则转化就出错了。
【将例题设计成情境串,先“比谁的面积大”,揭示转化策略,再“比谁的周长长”,丰富了转化形式。两次比较中,“转化前后,什么变了,什么没变?”的问题激发了学生对转化的深入反思。两次比较后,教师指出“等积变形”和“等长变形”的数学本质,这样的设计,可以有效地引导学生深刻感悟到实施转化的注意点:形式可以多样,但一定要等量转化。】
三、回顾旧知,领悟转化
师:请同学们回忆一下,我们曾经在学习哪些数学知识时,用到过转化的策略?
先小组交流,教师再选取学生的一些典型例子进行全班汇报。
小结:不理不知道,一理吓一跳啊!原来,我们一直在用转化策略啊!(学生微笑、点头)
师追问:(1)解决这些问题时,为什么要先转化?转化有什么好处?(2)转化时,用到了哪些具体方法?
同桌讨论,全班汇报后,相机板书:
复杂→简单 未知→已知
平移 旋转 割补 规律 性质……
【通过列举大量的例子,一方面,可以让学生感受转化策略应用的广泛性,转化的好处、转化的方法得以全面总结和展示;另一方面,使新旧知识之间很好地建立起了联系。】
四、梯度应用,丰富转化
1.小试牛刀。
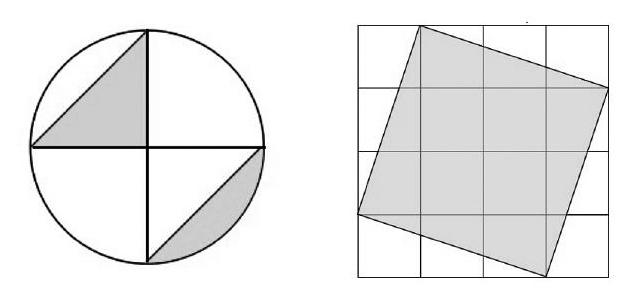
用分数表示下图中的涂色部分,并说说你是怎样转化的。
引导学生拿出学具,动手验证自己的想法。
指名一些学生上台展示,教师课件相机演示数方格法、分割平移法、分割旋转法以及数空白格法,并指出:同样都是旋转,用对了才管用;当别人都在数涂色部分时,不要忘了还可以转化一下思维——数空白部分。
过渡:对转化有感觉了吗?(有)能不能让这种感觉更好一些?其实,除了在图形中会用到转化,我们在计算领域也经常应用转化。
2.更进一步。
学生尝试用不同的方法计算。
指名学生上台展示或教师相机课件展示。
小结:同学们不仅会形与形的转化,还会把数转化成形。(板书:数形结合)数转化成形,数形结合,好不好?好在哪里?
正如数学家华罗庚所说:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休。” 3.走进生活。
最近,区里正在开展校园足球联赛。有16支球队参加比赛,比赛以单场淘汰制(即每场淘汰一支球队)进行。一共要进行多少场比赛才能产生冠军?
引导学生理解题意:单场淘汰制是什么意思?你能试试看吗?
预设:方法一:8+4+2+1=15(场);方法二:16-1=15(场)。
对于方法二,教师故作惊讶,引导学生解释。
比较:这两种方法有什么不一样的地方?
指出:方法一是从比赛过程的角度顺着想的,方法二是从比赛结果的角度逆着想的。考虑问题的角度不同,方法也会不同。(板书:换角度思考)
追问:如果有32支球队参赛呢?64支呢?n支呢?
拓展:据悉,晋级世界杯亚洲区预选赛的12支球队将分为两组再进行主客场双循环较量,前2名将直接获得参加世界杯决赛的资格,什么是双循环赛?要决出前2名,一共要进行多少场比赛?请同学们课后上网查一查、算一算,并和家长或体育老师交流!
【从小试牛刀(图形转化)到更进一步(数形转化),最后走进生活(足球淘汰赛问题),学生的思维得以进一步打开和丰富,认识到需要结合具体的问题来灵活选择转化的方法。】
五、交流总结,提升转化
师:这节课,我们一起学会了一种解决问题的策略——转化,你能用一两句话总结一下你的学习收获或感受吗?
学生展示后,相机出示一些数学家关于转化策略的名言。
师:古今中外,有许多善用转化策略的高手,除了前面提到的曹冲称象外,还有司马光砸缸、爱迪生巧测灯泡容积……在数学中善用转化的人是有智慧的人,在生活中善用转化的人是有创意的人!
(作者单位:南京市溧水区实验小学)
