竞标行为下的网络零售配送时隙动态定价策略

周诗宇，陈　雨，劳知雷，

（1.上海海事大学　经济管理学院，上海　201306；2.上海海事大学　交通运输学院，上海　201306）

竞标行为下的网络零售配送时隙动态定价策略

周诗宇1，陈雨2，劳知雷1，2

（1.上海海事大学经济管理学院，上海201306；2.上海海事大学交通运输学院，上海201306）

B2C环境下，对客户订单做出合理的配送定价对于网络零售商提高服务水平和最大化自身收益有重要意义。客户对网络零售配送服务的价格及价格变动尤为敏感，其多样化的购买行为和购买动机给网络零售商的销售预测与决策带来了极大的难度。针对网络零售商时隙价格维的收益管理，提出了一个基于消费者选择行为的时隙动态定价模型，结合动态定价与竞标行为以改善目前网络零售业固定时隙标价的缺失。通过算例分析发现客户到达率与类型比例的差异对时隙价格的影响，供网络零售商做拟订时隙价格策略的参考。

网络零售；配送时隙；动态定价；竞标行为

1　引言

时隙（time slot）在电子商务中是指网络零售商提供给消费者选择的订单产品送达的交货时间窗［1］。近十多年来，有鉴于全球经济快速发展，人们生活型态逐渐改变，消费型态也趋于多元化以及电子商务的发展，许多网络零售商都采取送货上门的配送模式。其中可观察到显著的变化是近年来因互联网科技的进步，改变了过去消费者在实体店面购物的习惯，进而带动了网络购物的风气，使得消费者居家即可购物，也显示出“宅经济”消费商机不容小觑［2］。随着消费者对送货上门物流服务需求量的增加，网络零售商所提供的配送服务也面临着越来越大的压力，而配送时隙价格的制定不仅影响网络零售商成本的配置，同时也反映了网络零售商的收益。相对于高峰时隙，低峰时隙配送的需求就减少许多，导致网络零售商有闲置成本问题的产生［3-4］。

价格在任何商业活动中都扮演了很重要的角色，尤其是在日益兴起的网络零售竞标行为配送服务中。Vulcano［5］从客户选择角度分析了定价对网络零售商收益的影响程度，并使用对需求进行合理的预测，以实现“削峰填谷”的效果。陈淮莉［6-7］针对客户选择时隙效用不同的特点，引入效用函数，建立基于多项Logit模型的选择概率公式，并对客户进行相应的分级，在价格折扣模型的基础上进行改进。于远光［8］通过模拟的方法综合分析了Stackelberg的市场结构中，抑价竞标和成本提升操纵在排污权拍卖中存在的情况，以及这两种相反的操作对于社会总体福利以及厂商间市场份额的影响。王宏［9］假设合谋竞标者在拍卖之前采用第二价格预拍的合谋机制，求解了第一价格拍卖下的合谋均衡。不但考虑了拍卖方对于合谋的最优策略性响应，而且考虑了参与合谋的竞标者与没有参与合谋的竞标者之间的策略性响应。严培胜［10］从项目拍卖者的角度，对交通BOT项目进行特许经营权机制设计，设计了一套科学合理的竞标机制来提高项目拍卖者对特许经营权的配置效率。

本文从提供送货上门物流服务的网络零售商的角度，探讨如何通过构建动态定价模型，分别决定高低峰竞标时隙的价格，并且诱使高峰时隙部分消费者需求转移到需求较少的低峰时隙，以达到均衡高低峰时隙配送需求的目标。与以往文献不同，利用竞标模型决定运费的高低来研究利润最大化，而并非折扣手段。将竞标与标价的概念引入动态定价模型中，客户首选与次选时隙的运费差异是通过各时隙需求（配送能力）大小来判定，网络零售商可以通过开放部分配送时隙来促使客户之间相互竞标，而不参与竞标的客户则能以时隙标价选择配送时隙。在允许消费者竞标行为后，网络零售商便可以通过给时隙订立最佳的价格来使得网络零售商总期望收益最大化。

2　模型描述与构建

本文主要探讨B2C网络零售在有限的配送能力约束下，在预定时间范围内，根据客户到达率与客户保留价格的变化分别决定高低峰竞标时隙的价格，使得网络零售商收益最大。客户选择或者未选择时隙可以当做是客户购买或者未购买时隙。为探讨目前实际所采用的时隙标价与动态价格的关系，本文将循序探讨三种时隙定价模型，对如何量化且优化配送时隙的标价与最低得标价格进行研究。

2.1符号说明与假设

集合：T表示客户预定时间t的集合，t∈T=｛0，1，…，h｝；P表示客户预定时间 pi的集合，pi∈P=｛p1，p2，…，pI｝。

参数：λ表示客户到达率；β表示竞标者占总客户群的比例；Ri表示客户对于配送时隙i的预期价格；ci表示剩余时隙能力的机会成本；α表示客户对时隙价格折价影响因子；θ表示剩余配送能力；Fˉ（p）表示客户的预期价格高于p值的累积概率函数；F（p）表示客户的预期价格低于p值的累积概率函数。

决策变量：p表示网络零售商所对时隙的价格；πp表示网络零售商总期望收益。

为不失一般性，假设客户竞标行为下的时隙定价模型存在：

（1）选择某一天配送的客户到达服从泊松分布；（2）不考虑当天配送的情况，即不考虑当日的配送时隙选择；（3）不考虑订单取消和退货情况；（4）当配送能力确定之后，若零售商对订单做出承诺，就能按时送达，不考虑意外情况。

2.2单一配送时隙但尚未考虑竞标行为下的时隙定价模型Ⅰ

目前网络零售业最常见的时隙定价模型主要为固定价格，即配送时隙价格并不会因剩余配送能力θ、预定时间t和客户到达率λ的变化而有所改变。在此模型下，只考虑两种类型的客户行为（即价格接受客户和放弃购买客户）。网络零售商收益πp完全来自于价格接受者的客户类型，若无法接受配送时隙标价的客户将放弃购买，如图1所示。

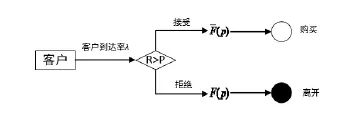
图1　模型Ⅰ仿真流程图

模型的目标函数为最大化的总期望收益，其数学式如下所示：

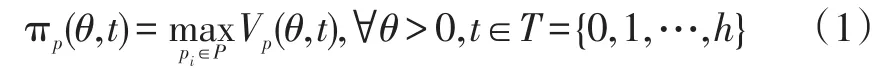
其中：

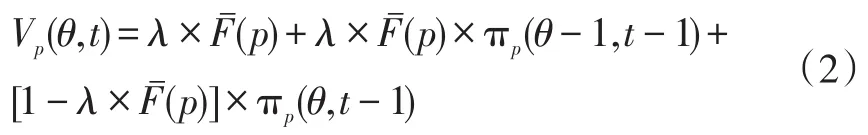
2.3单一配送时隙且考虑竞标行为下的时隙定价模型Ⅱ

模型Ⅱ为模型Ⅰ的延伸，假定配送时隙价格如同模型Ⅰ为一决策变量，伴随着剩余配送能力θ、剩余预定期数t以及客户到达率λ而有所变动。此模型的客户类型包括价格接受者和投标者。对价格接受者而言，当预期时隙保留价格高于标价或进行竞标交易的成本过高时，客户宁愿以配送时隙标价交易而非竞标；对投标者而言，当心目中对时隙的保留价格低于标价，投标者会以保留价格进行竞标交易，如图2所示。

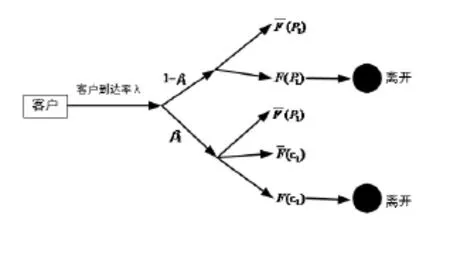
图2　模型Ⅱ仿真流程图

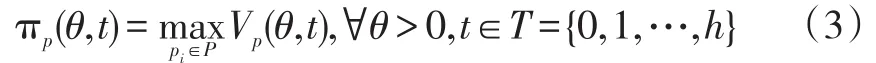
其中：

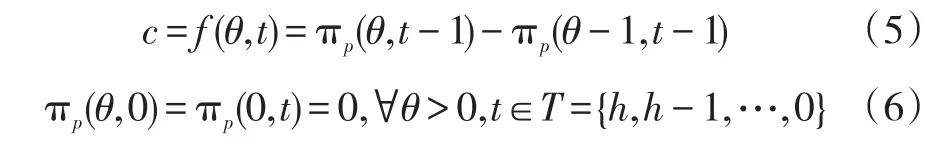
公式（4）表示当预定时间为t时，客户选购可能出现的五种情况：①预定时间为t时，客户是价格接受者并且最终购买时隙；②预定时间为t时，客户是价格接受者并且最终放弃购买时隙；③预定时间为t时，客户是对时隙有保留价格介于标价与最低可接受的竞标价格之间的竞标者并且最终购买时隙；④预定时间为t时，客户是对时隙的保留价格高于标价的竞标者并且购买时隙；⑤预定时间为t时，客户是对时隙的保留价格小于最低可接受的竞标价格的竞标者并且放弃购买时隙。式（5）-（6）表示配送时隙的机会成本以及边界条件。

3　算例分析

3.1情境设计

为了验证模型和算法的正确性和有效性，现通过算例来进行验证。从两种定价模型中可以发现，将预订时间范围划分为h个离散时间段，则剩余预定期数为T。假设每个时间段足够小，有且只有一个客户订单到达事件发生或者没有客户订单到达，并且单位客户订单消耗单位配送能力，即每一个预定时间段的配送能力一次仅会减少一单位或维持原配送能力。假定客户到达率λ为0.8；预定时间划分为5个离散时间段（剩余预定期数为5）；剩余配送能力θ为3单位；客户保留价格的累积概率函数服从韦伯分配（形状参数为2，尺度参数为80）。

3.2结果分析

模型Ⅰ配送能力与配送时间对收益的影响如图3所示，矩阵π（θ，t）为剩余配送能力所对应剩余预定期的最佳时隙价格与总期望收益表。可以发现，矩阵π（3，3）可推知在一期预定结束后，消耗单位配送能力期望总收益为82.84，最佳时隙价格为57，各期最佳时隙价格波动是前一期消耗配送能力与否所决定的，举例而言，π（3，3）由π（3，2）与π（2，2）所组成，其中π（3，2）与π（2，2）的最佳时隙价格与总期望收益数值相同，因此在计算π（3，2）的最佳时隙价格与总期望时，最佳时隙价格并未改变。所以，当剩余配送能力小于剩余预定期数，最佳时隙价格会随预定期数的减少而波动，网络零售商在时隙预定初期可提高时隙标价以增加总期望收益。

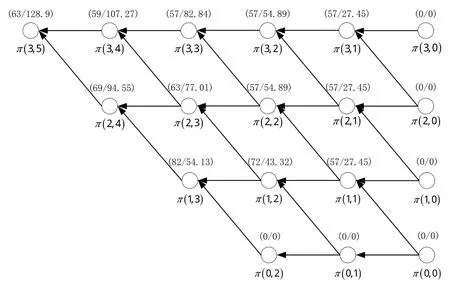
图3　模型Ⅰ（θ=3，T=5）配送能力与配送时间对收益的影响

延续模型Ⅰ的参数设定，模型Ⅱ中将客户区分为价格接受者与投标者，并假定β=1-β=0.5，即投标者与价格接受者的比例皆各半；客户在看到时隙标价后对该时隙价格的折价率α=0.5。图4是模型Ⅱ剩余配送能力所对应剩余销售期的最佳时隙价格与总期望收益表。比较模型Ⅰ、模型Ⅱ的结果可知，在模型Ⅱ纳入异质性客户类型后，最佳时隙价格不仅大幅提高，收益幅度也随之增加。所以，网络零售商可从保留价格较高的潜在客户获取更多的收益并假设投标者占总客户群的比例。

图4　模型Ⅱ（θ=3，T=5）配送能力与配送时间对收益的影响

从图5、图6可观察到，模型Ⅱ的最佳时隙价格结果较模型Ⅰ的最佳时隙价格高，且不会因提高时隙价格而流失部分客户收益，反而更能提高总期望收益，收益成长百分比在此例子下从1.13%上升到8.74%。

3.3敏感度分析

（1）客户到达率λ的影响。首先，分析模型Ⅰ客户到达率λ分别为0.2、0.5、0.8时对最佳时隙价格与总期望收益的影响。

图5　模型Ⅰ与Ⅱ的最佳时隙价格

图6　模型Ⅰ与Ⅱ的期望收益

由图7、图8可知，客户到达率的高低会影响最佳时隙价格的订定，进而影响总期望收益。随着客户到达率越高，网络零售商能订定更高的最佳时隙价格，总期望收益也会随之增加。

（2）投标者比例β的影响。在模型Ⅱ中，客户到达率为0.8的情况下，分析投标者比例β值的不同（0.3，0.5，0.7）对最佳时隙价格与总期望收益的影响。

由图9、图10可知当投标者比例越小时，价格接受者的比例越高，同时最佳时隙价格越低。其中，主要原因为当价格接受者比例高于投标者比例时，表示网络零售商收益主要源自于价格接受者，若网络零售商订定过高的时隙标价，反而会流失保留价格较低廉的潜在价格接受者。因此，当投标者比例越小，网络零售商对时隙应订定较低的时隙标价以获取较高的期望收益。反之，当投标者比例越大时，网络零售商对时隙应订定较高的时隙标价，主要原因是因为在本节设计中，投标者会在观察网络零售商对时隙所提供的标价之后，依照心目中对时隙的保留价格与标价相互衡量后竞标。因此，网络零售商若订定较高的时隙标价可获取更多潜在投标者的收益。

图7　模型Ⅰ客户到达率与最佳时隙价格的关系

图8　模型Ⅰ客户到达率与期望收益的关系

图9　模型Ⅱ中投标者比例与最佳时隙价格的关系

图10　模型Ⅱ中投标者比例与期望收益的关系

4　结语

本文从两种定价模型出发：数学模型Ⅰ为现行时隙定价机制，数学模型Ⅱ则引入动态定价机制以改善模型Ⅰ固定时隙定价且未探讨消费者行为的缺失。将动态定价和竞标行为结合，以改善目前网络零售业固定时隙标价的缺陷，试图探讨客户到达率与客户类型比例的差异对时隙价格的影响，供网络零售商做拟订时隙价格策略的参考方针。通过算例分析可以发现，动态定价机制（模型Ⅱ）收益百分比表现较现行固定时隙定价机制（模型Ⅰ）至多可改善8.7%，其中当剩余配送能力小于剩余预定期数时，网络零售商在预定初期可提高时隙标价以增加总期望收益，因此时隙标价机制订定基本时隙价格，再由动态定价机制决定消费者欲指定配送时隙需额外支付的运费。此外，通过分析客户到达率λ与客户类型比例的差异对配送时隙价格的影响，供网络零售商做拟订配送时隙价格策略时做参考。随着客户到达率越高，网络零售商可以订定更高的最佳时隙价格，总期望收益也会随之增加。再者，当投标者占全体客户比例不到一半时，网络零售商应该采用模型Ⅰ的时隙标价机制。

本文通过动态定价模型，不仅缩短高低峰配送时隙需求的差距、提高配送能力使用率，进而网络零售商可以通过诱使高峰时隙部分消费者需求转移到需求较少的低峰时隙，以均衡高低峰时隙配送需求，提高网络零售商总体收益；从客户方面来说，客户能在可接受配送费用范围中选择欲配送时隙，减少平均等候时间。

为使研究更贴近实际，未来可以制定更完善的竞标机制，并更进一步探讨客户选择行为与不同竞标机制策略的关系，决定某些时隙可开放竞标促使达到转移高峰需求配送时隙至低峰需求配送时隙与提高网络零售商收益的目的。

［1］Agatz N，Campbell A，Fleischmann M，et al.Time slot management in attended home delivery［J］.Transportation Science， 2011，45:435-449.

［2］Asemir K，Jacob V，Krishnan R.Dynamic pricing of multiple home delivery options［J］.European Journal of Operational Research，2009，196:246-257.

［3］Campbell A，Savelsbergh M.Incentive schemes for attended home delivery services［J］.Transportation Science，2006，40:327-341.

［4］Campbell A，Savelsbergh M.Decision support for conmuser direct grocery initiatives［J］.Transportation Science，2005，39:313-327.

［5］Vulcano G，Van G，Chaar W.Choice-based revenue management:An empirical study of estimation and optimization［J］. Manufacturing Service Operation Management，2010，（12）:371-392.

［6］陈淮莉，徐朗.网络零售配送时隙差异化定价与折扣激励［J］.上海海事大学学报，2015，（2）:49-54.

［7］陈淮莉，卫亚运.基于客户选择行为的网络零售配送时隙定价模型［J］.安徽大学学报（自然科学版），2014，（38）:6-11.

［8］于远光，孟凡强.不完全竞争市场下排污权拍卖的价格操纵分析［J］.统计与决策，2009，（11）:41-43.

［9］王宏，陈宏民，顾巧明.基于第二价格预拍的竞标者合谋均衡分析［J］.中国管理科学，2010，18（3）:132-140.

［10］严培胜，王先甲.交通BOT项目特许经营权竞标机制设计［J］.中国管理科学，2009，17（4）:97-102.

Dynamic Distribution Time-slot Pricing Strategy for Online Retailers with Bidding Behavior

Zhou Shiyu1，Chen Yu2，Lao Zhilei1，2
（1.School of Economics&Management，Shanghai Maritime University，Shanghai 201306；2.School of Traffic&Transportation，Shanghai Maritime University，Shanghai 201306，China）

In this paper，in view of the returns management of the time-slot price dimension of an online retailer，we proposed a distribution time-slot dynamic pricing model based on consumer selection and then combined it with the bidding behavior so as to supplement the current lack of fixed time-slot pricing in the online retailing industry.Then，through a numerical example，we identified the influence of customer arrival ratio and proportion on the time-slot price.

online retailing；distribution time-slot；dynamic pricing；bidding behavior

F724.6；F724.2

A

1005-152X（2016）06-0058-05

10.3969/j.issn.1005-152X.2016.06.014

2016-05-14

上海市自然科学基金资助项目（12ZR1412800）；上海市教委科研创新项目（12YZ119）

周诗宇，女，宁夏人，上海海事大学经济管理学院学生；陈雨，男，上海人，上海海事大学交通运输学院学生；劳知雷（1974-），男，上海人，博士研究生，讲师，研究方向：交通运输规划与管理。