高空螺旋桨无刷直流电机重置粒子群PID控制
2016-10-29杨剑威窦满峰骆光照赵冬冬
杨剑威,窦满峰,骆光照,赵冬冬
(西北工业大学自动化学院,陕西西安 710072)
高空螺旋桨无刷直流电机重置粒子群PID控制
杨剑威,窦满峰,骆光照,赵冬冬
(西北工业大学自动化学院,陕西西安 710072)
永磁无刷直流电机驱动高空螺旋桨负载时,由于大气密度随海拔高度变化,电机转速随螺旋桨负载变化不断波动,传统定参数PID控制难以随环境变化对电驱动系统PID控制参数进行实时调整,系统的动态特性和鲁棒性较差。提出一种基于BFGS(Broyden-Fletcher-Goldfarb-Shanno)动态重置粒子群算法(BFGS-RPSO)的永磁无刷直流电机PID参数控制方法,该方法利用BFGS-RPSO算法灵活快速的在线参数寻优特点,对永磁无刷直流电机控制系统PID参数进行在线实时优化调整,提高了螺旋桨负载电驱动系统的动态特性和鲁棒性。Matlab仿真和实验表明,电机在起动过程中,转速上升时间较短,转速和转矩超调较小,且在负载波动过程中电机转矩脉动较小,BFGS-RPSO PID参数控制比传统PID控制具有更好的动态特性和鲁棒性,适合应用于高空螺旋桨永磁无刷直流电机螺旋桨电驱动系统。
永磁无刷直流电机;电驱动系统;高空螺旋桨;重置粒子群算法;PID参数控制
永磁无刷直流电机采用稀土永磁体励磁,没有励磁损耗,效率高,功率密度高,且采用电子换向,解决了直流电机换向火花、噪声及摩擦因素等问题,在工业领域中得到了广泛的应用[1-2]。
永磁无刷直流电机控制中较常用的定参数PID控制方法,具有算法简单、易于实现等优点,在一般电驱动系统中得到了广泛的应用,但由于永磁无刷直流电机具有时变、非线性、强耦合等特点,传统定参数PID控制方法的控制参数不能随环境变化而调整,不具有整体优化功能,加之高空螺旋桨负载转矩受大气密度影响,并随海拔高度不断变化,波动较大,传统定参数PID控制方法较难满足高精度系统的静动态性能指标,在保证系统的快速性和鲁棒性等方面都无法得到满意的效果[3-4]。
针对这种情况,本文提出一种新的永磁无刷直流电机驱动螺旋桨负载的控制方法,基于BFGS动态重置粒子群算法(BFGS-RPSO)的永磁无刷直流电机PID参数控制方法。该方法利用BFGS-RPSO算法灵活均衡的全局寻优和快速的局部寻优能力,对永磁无刷直流电机控制系统PID参数进行在线寻优。通过理论分析及仿真和实验,该方法与传统PID控制相比,电机在启动过程中,转速上升时间短,转速和转矩超调小,且在负载波动过程中,电机转矩波动小。该方法提高了控制系统的PID参数在线优化能力,比传统PID控制具有更好的动态特性和鲁棒性,适合应用于永磁无刷直流电机螺旋桨负载电驱动系统。
1 永磁无刷直流电机模型
永磁无刷直流电机每相绕组的相电压由相电阻压和绕组感应电动势组成,假设磁路不饱和,并根据基尔霍夫电压定律可得三相定子绕组电压方程为
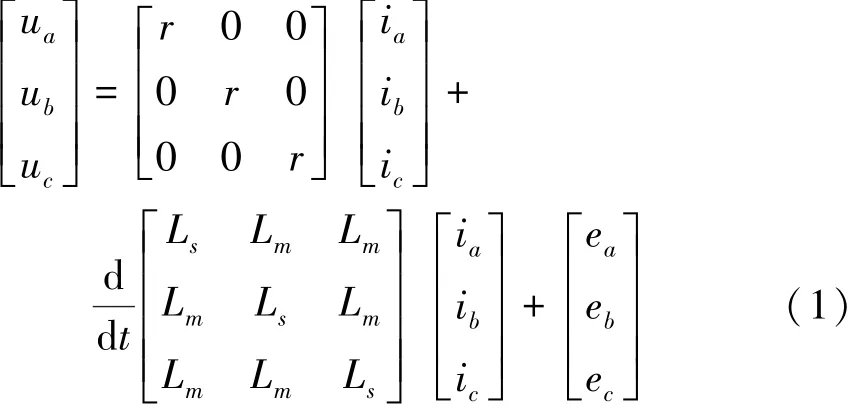
式中:ua、ub和uc为三相定子绕组相电压(V);r为三相定子绕组的电阻(Ω);ia、ib和ic为三相定子绕组相电流(A);Ls为定子每相绕组的自感(H);Lm为定子任意两相绕组之间的互感(H);ea、eb和ec为三相定子绕组反电动势(V)。
由于定子绕组采用Y型绕组接法,且无中线,故有

于是有
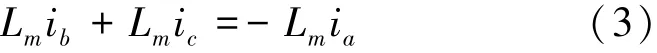
将(3)式代入(1)式得三相永磁无刷直流电机数学模型的状态空间表达式为
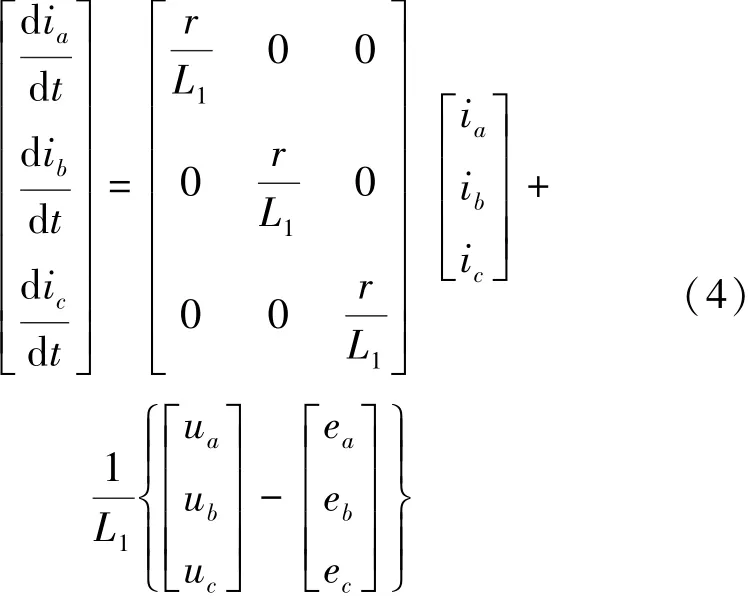
式中,L1=Ls-Lm为定子每相绕组的等效电感。
电机运行过程中,忽略转子的机械损耗和杂散损耗,从能量传递角度分析可得定子三相绕组的输入功率与所产生的电磁转矩之间关系如(5)式、(6)式所示:
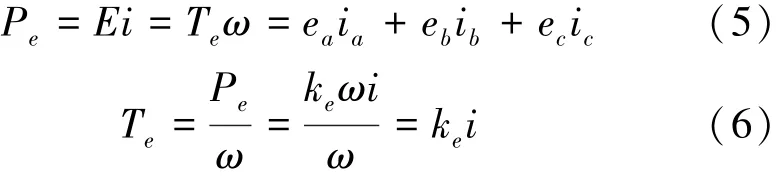
式中:Pe为电磁功率(W);E为三相定子绕组反电动势(V);Te为电磁转矩(N·m);ω为电机的角速度(rad·s-1);Ke为反电动势系数。
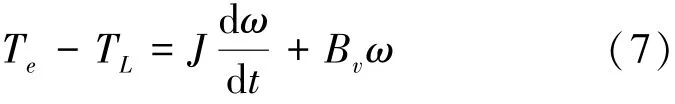
式中:TL为负载转矩(N·m);J为转子转动惯量(kg ·m2);Bv为阻尼系数(N·m·s)。
永磁无刷直流电机的电磁转距、负载转矩以及转速之间的关系可用电机的机械运动方程来描述,如(7)式所示
2 螺旋桨负载特性分析
螺旋桨负载与一般电机负载有所不同,永磁无刷直流电机在驱动螺旋桨负载时,螺旋桨桨叶倾角的变化即为负载的变化。螺旋桨输入为永磁无刷直流电机的转速nL,输出为螺旋桨转矩TL,螺旋桨的转速和转矩关系表示为[5-6]

式中:CT为转矩系数(N·m·s);ρ为大气密度(kg/m3);nL为螺旋桨转速(r/min);D为螺旋桨直径(m),取决于螺旋桨的几何参数。
螺旋桨的转矩特性为电机转速的二次曲线(TL∝n2),与电机的机械特性曲线相交,所以电机的运行和调速必须满足螺旋桨的负载特性。同时,螺旋桨的转矩特性还与大气密度相关,随着海拔高度的变化,螺旋桨的转矩会发生变化。图1是通过相关实验和推导计算得出的不同高度下螺旋桨的转速转矩特性。
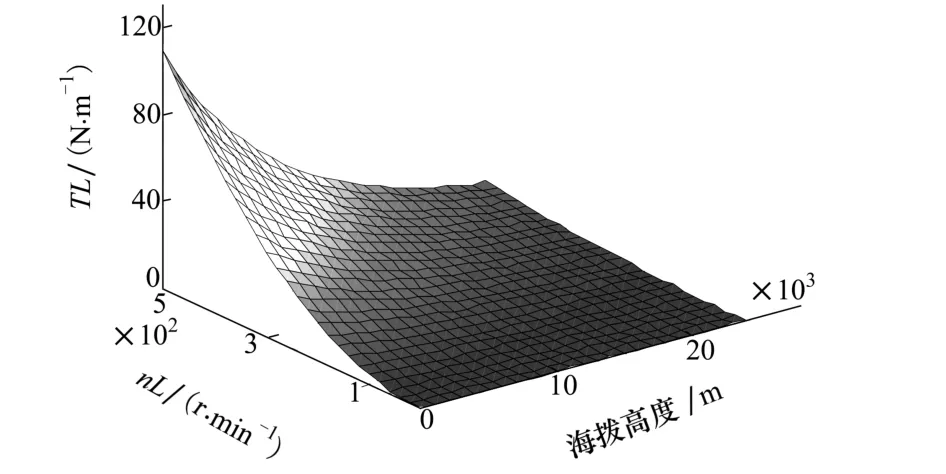
图1 不同高度下螺旋桨的转速转矩特性
由图1可以看出,同一转速下,高度越高,螺旋桨的转矩越小。对于大驱动转矩系统,提高螺旋桨转矩势必要增加螺旋桨桨叶直径[7-8]。而螺旋桨桨叶直径增大,螺旋桨的转动惯量也会随之增大,这将导致永磁无刷直流电机在启动、加减速以及制动过程中,可能会出现不平稳现象;尤其是在低速时,系统可能会出现抖动,使系统可靠性降低。因此,驱动控制器应根据螺旋桨负载的变化特点对电机的PID控制参数进行相应调整。
3 粒子群PID参数控制
3.1粒子群算法原理
粒子群算法(PSO)是一种群体智能优化算法,由Kennedy博士和Eberhart博士于1995年提出。粒子群算法源于鸟群在寻觅时的行为,并发展为一种基于迭代的有效优化工具。粒子群算法的进化过程仅需要2个方程,根据鸟群觅食的规律进行自然类比,可以很容易对方程的参数进行设置。粒子群算法不需要目标函数的梯度信息,只需要通过适应度(fitness value)函数评估可行域内的状态位置。因此,粒子群算法能够被应用于任何实值优化问题,是一种有效且便于应用的优化工具[9-10]。
粒子群算法首先将在目标函数f(x)的n维可行域内随机初始化粒子群中的每一个粒子
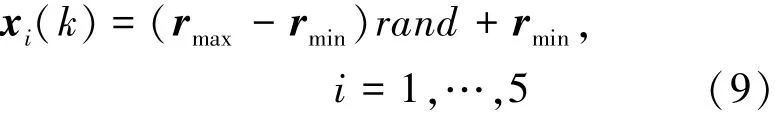
式中,rmax,rmin∈Rn为目标函数可行域的上、下限向量;rand为服从[0,1]分布的随机数。第i个粒子在n维空间中以一定的速度飞行,该粒子的当前状态由一个n维位置向量xi=(xi1,xi2,…xin)和一个n维速度向量vi=(vi1,vi2,…vin)来表示。位置向量决定粒子在可行域中的当前位置,速度向量决定粒子进化飞行的方向和距离。每个粒子i都有一个由目标函数决定的适应值,并根据适应度确定自己到目前为止发现的最好位置Pbest,记为Pi=(Pi1,Pi2,…Pin),这被视为粒子自身的飞行经验。对于最小值优化问题,更新方程可以表示为
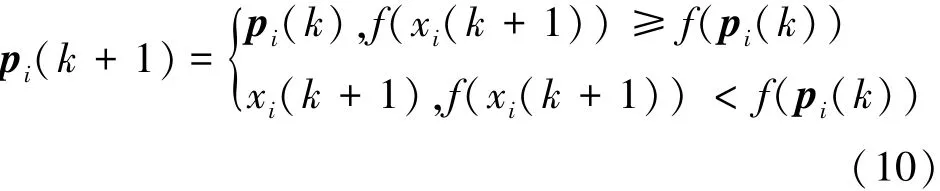
式中,k为迭代次数。另外,通过比较每一个粒子的适应度,可以确定到目前为止整个粒子群中所有粒子发现的最好位置Pgbest,记为Pg=(Pg1,Pg2,…Pgn),可看作是同伴经验,更新方程表示为
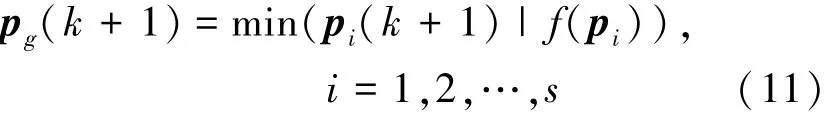
式中,s为粒子群粒子个数。粒子通过学习自己的经验和同伴的经验来决定下一步的运动。粒子i的飞行轨迹由下面的更新方程决定:
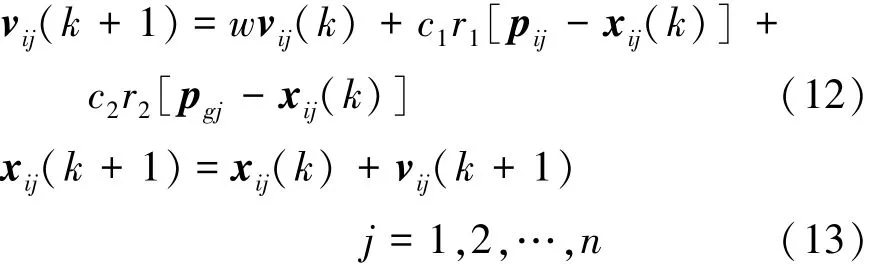
式中,w为惯性权重值;c1,c2为正的加速常数;r1,r2是服从[0,1]分布的随机函数;j是更新的坐标。根据(12)式、(13)式,每一个粒子逐一更新速度、位置向量的每一维[11]。
3.2BFGS-RPSO算法
标准粒子群算法在诸多优化问题中,特别是对多变量、多峰优化的问题,常会遇到收敛早熟和收敛速度慢的问题[12]。很多改进粒子群算法的核心思想是通过提高粒子群的多样性或提高全局搜索能力降低算法发生收敛早熟的概率。但多数改进粒子群算法,如变参数粒子群算法、混合粒子群算法和邻域粒子群算法,并无法从根本上消除收敛早熟问题;同时上述改进粒子群算法改善全局搜索能力的代价是降低算法的局部搜索能力和收敛速度。
重置粒子群算法有别于其他改进粒子群算法,由于包含收敛早熟检测环节和粒子群重置环节,重置粒子群算法能够完全避免收敛早熟发生。BFGS (Broyden-Fletcher-Goldfarb-Shanno)动态重置(dynamic reinitialization)PSO(BFGS RPSO)算法将粒子群搜索过程分为“全局搜索”、“局部搜索”和“动态重置”3个阶段,从多个方面改善了重置粒子群(RPSO)算法的性能。
“全局搜索”阶段表示当前每一个子群都不存在收敛早熟的趋势,粒子群保持丰富的多样性。此时,采用Neumann粒子群算法,利用该算法保持粒子群的多样性,增加搜索全局最优值的能力,并保证较快的收敛速度。“局部搜索”阶段表示当前至少有一个子群的粒子收敛到一个局部或全局极值点的邻域内,并且在该邻域内没有比极值点更好的位置向量,子群的所有粒子将无法摆脱当前极值点的吸引,最后全都收敛于极值点,表现出收敛早熟的趋势。此时,利用BFGS算法加强局部搜索能力,发挥其收敛速度快、收敛精度高和稳定性强的优点。BFGS算法是基于梯度信息的进化方法,不需要粒子间进行信息交换,仅需对子群中的全局最优值Pl进行迭代搜索,子群内其他粒子不进行BFGS迭代,有利于减少算法的计算量。“动态重置”阶段表示当前有或至少有一个子群的Pl收敛到极值点,该子群发生收敛早熟。此时,不改变其他子群的搜索状态的同时对发生收敛早熟的子群进行重置操作。“动态”表示重置的子群数或粒子数是变化的,可合理解决重置粒子数对算法的影响。“动态重置”不但消除了子群收敛早熟问题,而且保证其他子群能充分利用当前信息,减少重复搜索,提高搜索效率,通过对部分粒子在可行域内重置,实现粒子间信息交换,从而提高了速度和效率。
在BFGS-RPSO算法中,分别定义2个判定条件,“条件一”和“条件二”。“条件一”并不是检测粒子群的收敛早熟状态,而是检测子群出现收敛早熟趋势的时刻,即从“全局搜索”向“局部搜索”转换的时刻。最优的转换时刻是子群内所有粒子位于极值所在的凸脊或凹谷边缘的时刻,即极大值或极小值边缘的时刻。因此,一般的PSO收敛早熟检测条件均无法有效达到“条件一”的目的,且最大群半径(maximum swarm radius,MSR)检测条件的阈值若选择过大,则会导致同一个邻域内的粒子收敛于不同极值,最终导致后续的重置操作无法实现,算法彻底失败,阈值若选择过小,则无法充分发挥BFGS算法局部搜索的速度优势,导致搜索速度减慢,搜索效率降低。针对这一情况,“条件一”采用复合重置条件:当邻域内所有粒子适应度有相同的斜率符号时,适当扩大MSR,用最大群半径与目标函数斜率(objective function slope,OFS)结合的方式共同定义“条件一”,即MSR+OFS。则归一化检测条件可以表示为
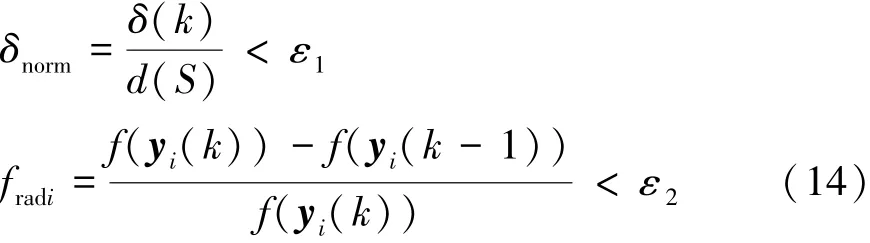
式中,δ(k)为第k次迭代群半径,定义为任意粒子与全局最优粒子Pg之间的最大欧几里得距离,d(S)表示可行域S的直径,阈值ε1一般取1.1×10-6~1.1×10-4,阈值ε2一般取10-10效果较好。
由于“局部搜索”模式采用BFGS搜索策略,所以“条件二”定义为局部最优粒子适应度梯度,若满足
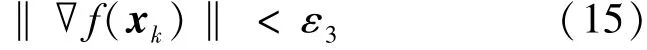
表示通过局部搜索,子群收敛于极值,进一步的搜索无法显著增加适应度的精确度,阈值ε3一般取10-16效果较好。
3.3BFGS-RPSO PID参数优化控制
永磁无刷直流电机控制系统结构框图如图2所示。
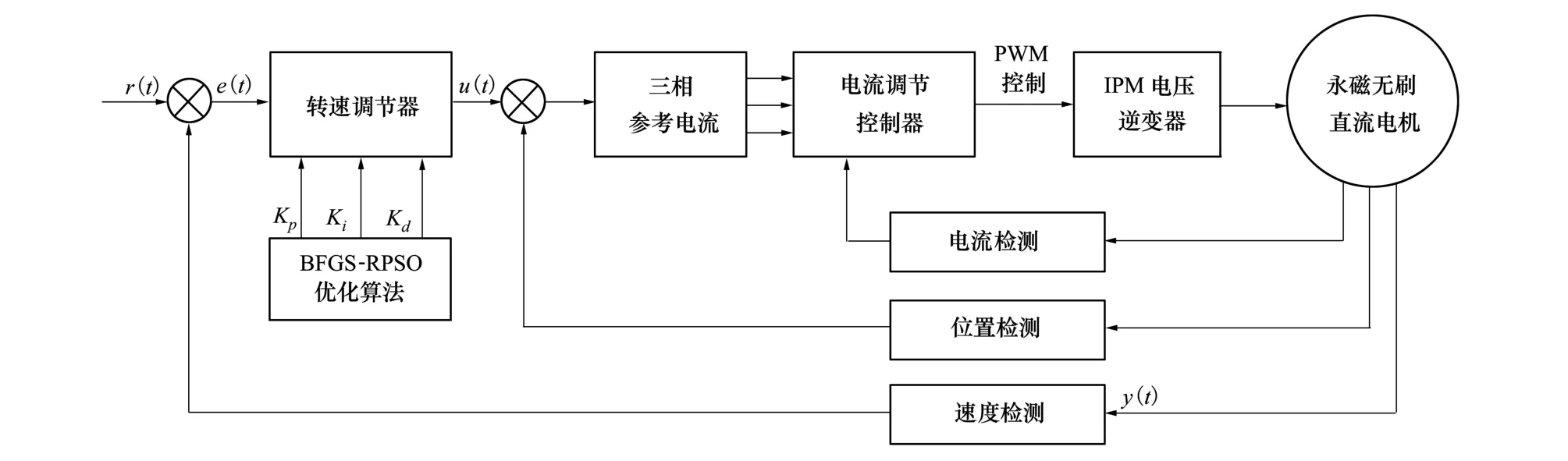
图2 永磁无刷直流电机控制系统结构框图
图中r(t)为给定电机转速,y(t)为反馈转速, e(t)为转速误差,u(t)为PID控制器输出电压。其中:
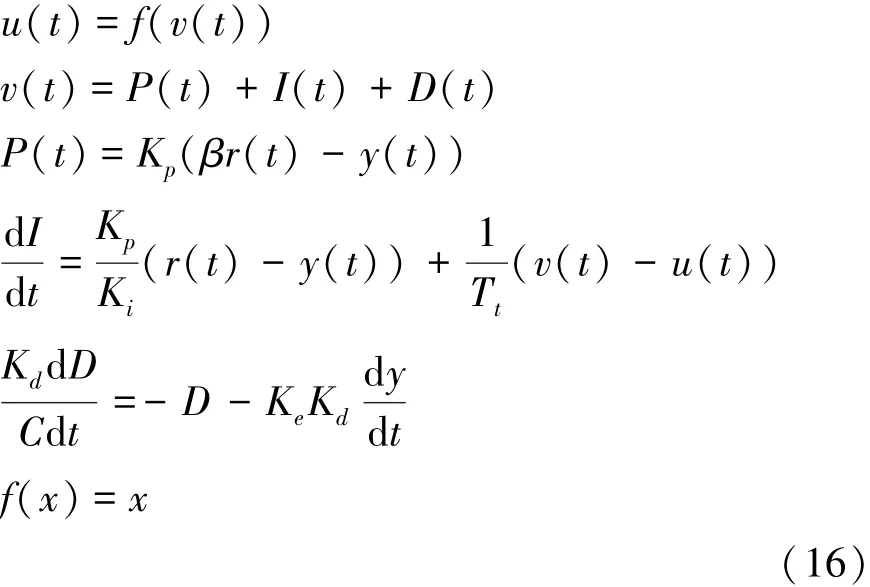
式中Tt为时间常量;C为常系数,通常取值10;Kp、Ki、Kd为BFGS-RPSO算法PID参数优化控制的3个参数;dI/dt为积分越界消除。
在BFGS-RPSO PID参数优化控制中,利用BFGS-RPSO算法优化PID控制器中的Kp,Ki,Kd3个参数,将这3个参数看作粒子群中的3个粒子,在搜索空间中找到最优的位置就是最优的PID参数。BFGS-RPSO PID参数优化控制的程序步骤为:
1)初始化粒子的位置向量x(i)和速度向量v(i);
2)以当前的粒子位置作为PID参数,按照(16)式计算控制量u(t),得出转速误差e(t);
3)循环步骤(2)得到绝对误差积分,作为粒子i适应度评价标准A(i);
4)根据适应度定义粒子i当前最优值Pi(i),子群j当前最优值Pi(j)和当前全局最优值Pg;
5)计算子群j的“条件一”和“条件二”;
6)检测子群j的“条件一”,如果成立则F(j)=1;检测子群j的“条件二”,如果成立则S(j)=1:
7)当F(j)=0、S(j)=0,子群j处于“全局搜索”阶段,采用Neumann PSO继续进行搜索;
8)当F(j)=1、S(j)=0,子群j处于“局部搜索”阶段,采用无导数拟牛顿BFGS算法对子群中的Pi(j)继续进行搜索;
9)当F(j)=1、S(j)=1,子群j处于“状态重置”阶段,将子群j内所有粒子位置向量在可行域内进行重置,速度向量重置为零向量,令F(j)=0、S(j)=0;
10)计算粒子i的适应度A(i);
11)根据适应度定义粒子i当前最优值Pi(i),子群j当前最优值Pi(j)和当前全局最优值Pg;
12)如果F(j)=0,计算子群j的“条件一”;如果F(j)=1,计算子群j的“条件二”;
13)满足程序停止条件,程序终止;否则返回第7)步。
理论上,当迭代次数趋于无穷时,BFGS-RPSO算法能够以任意精度逼近全局最优值。但是考虑到PID转速控制的时效性以及控制系统的安全性,在在线寻优过程中,Kp,Ki,Kd3个待寻优参数均会设置取值范围,且规定BFGS-RPSO算法程序停止条件为适应度A(i)满足收敛阈值或程序达到最大允许适应度计算次数(MaxEva.)。本系统粒子群规模20,由于只有Kp,Ki,Kd3个待寻优参数,搜索空间维数为3,搜索空间维数不高,最大允许适应度计算次数设置为MaxEva.=100即可满足对PID控制参数的寻优。
4 仿真及实验分析
4.1仿真实验
为了验证BFGS-RPSO永磁无刷直流电机PID控制方法的正确性,利用Matlab/Simulink工具,搭建了基于BFGS-RPSO算法的永磁无刷直流电机控制系统仿真模型。仿真中,永磁无刷直流电机螺旋桨电驱动系统的参数设置为:驱动电机额定功率P=3 kW,额定电压U=270 V,额定转速n=3 000 r/ min,电机极对数p=2,电机定子绕组相电阻r=0.15 Ω,电机定子绕组电感L=1.69 mH,驱动电机转动惯量JM=0.000 9 kg·m2,折算到电机上的螺旋桨负载转动惯量JL=0.2 kg·m2。
图3为采用传统定参数PID控制时电机的转速响应曲线;图4为采用BFGS-RPSO PID参数优化控制时电机转速和转矩响应曲线。从图3可以看出,在传统定参数PID控制下,电机启动时,转速上升时间约为0.05 s,转速上升时间较长,转速响应慢,系统的动态性能较差;而从图4a)中可以看出,与传统定参数PID控制相比,本文提出的BFGS-RPSO PID参数优化PID控制方法,在永磁无刷直流电机螺旋桨负载电驱动系统启动时,转速上升时间约为0.02 s,比传统定参数控制启动时间缩短了近60%,转速上升时间短,响应快,超调小,系统的动态性能较好;从图4b)中可以看出,在电机启动时,BFGSRPSO PID参数优化控制方法的转矩响应时间约为0.05 s,在电机运行平稳后,突加负载,转矩响应时间约为0.05 s,且转矩超调较小。仿真结果表明BFGSRPSO PID参数优化控制比传统PID控制具有更好的动态特性和鲁棒性。
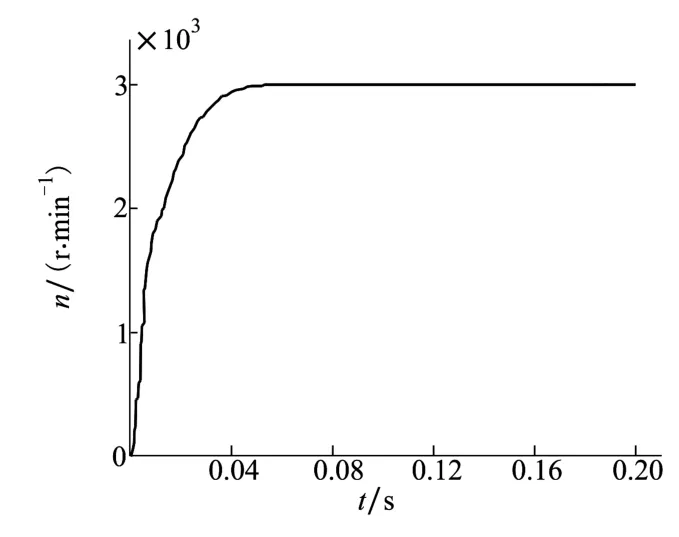
图3 传统定参数PID控制电机的转速响应曲线

图4 BFGS-RPSO PID控制时电机转速和转矩响应曲线
4.2实验结果
实验以TI公司的32位高性能数字信号控制器TMS320F2808为基础,搭建了永磁无刷直流电机螺旋桨电驱动系统实验平台。实验样机采用带Hall位置传感器的3 kW无刷直流电机,控制电路硬件框图如图5所示,实验装置如图6所示。
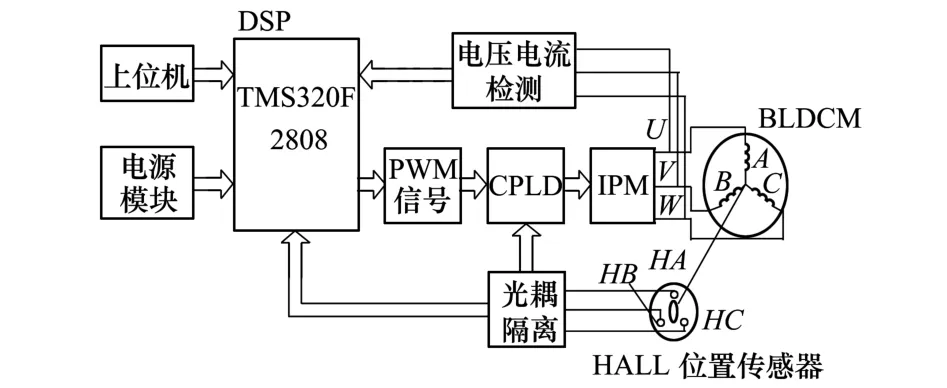
图5 BLDCM控制系统硬件框图

图6 电机实验装置图
在实验中,为保证上位机和下位机通讯的可靠性,以及返回数据的准确性,上位机通过CAN总线和RS422串口对系统进行异构双余度通信控制,电机转速通过Hall位置信号进行计算得到,并通过CAN总线或RS422串口通信传送到上位机保存。实验中电机带负载启动,负载转矩1 Nm,给定转速3 000 r/min,当电机运行平稳之后,对系统突加负载,负载转矩从1 N·m突变为3 N·m。利用Matlab软件分别将传统定参数PID控制和BFGSRPSO PID控制下启动和负载突变时的转速数据绘制为转速响应曲线,如图7~图8所示。通过对比图7和图8可以看出,传统定参数PID控制下,电机在启动时,转速上升时间较长,转速响应慢,系统的动态性能较差,而BFGS-RPSO PID参数优化PID控制方法的启动时间相比于传统定参数PID则大幅缩短,转速上升时间短,系统的动态性能较好。通过对比图9和图10,可以看出,BFGS-RPSO PID控制的抗扰动能力明显优于传统定参数PID控制,鲁棒性更好,更适合应用于高空螺旋桨负载转矩不断波动变化的情况下。

图7 传统PID控制电机启动时实测转速曲线
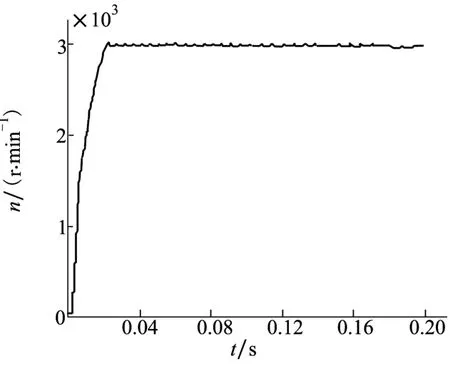
图8 BFGS-RPSO PID控制电机启动时实测转速曲线
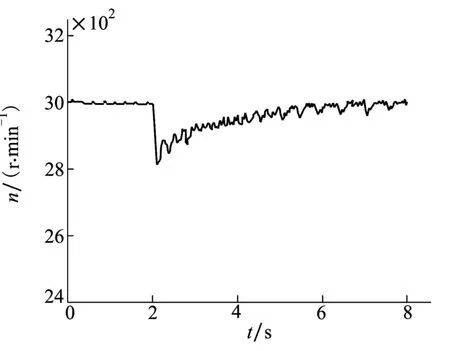
图9 传统PID控制电机负载突变时实测转速曲线
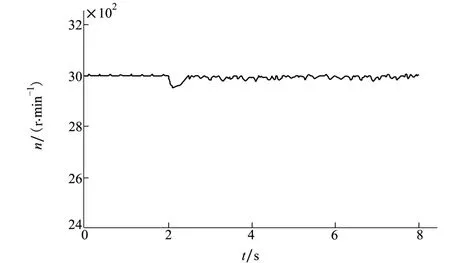
图10 BFGS-RPSO PID控制电机负载突变时实测转速曲线
5 结 论
本文针对永磁无刷直流电机驱动螺旋桨负载时,由于大气密度随海拔高度变化,电机转速随螺旋桨负载变化不断波动,传统定参数PID控制难以随环境变化对电驱动系统PID控制参数进行实时调整,系统的动态特性和鲁棒性较差的问题,提出一种新的永磁无刷直流电机驱动螺旋桨负载的控制方法,基于BFGS动态重置粒子群算法的永磁无刷直流电机PID参数控制方法。该方法利用BFGSRPSO算法灵活均衡的全局寻优和快速的局部寻优能力,对永磁无刷直流电机控制系统PID参数进行在线优化,提高了螺旋桨负载电驱动系统的动态特性和鲁棒性。最后通过仿真和实验表明,与传统定参数PID控制相比,BFGS-RPSO永磁无刷直流电机PID参数控制方法,在电机启动过程中,转速上升时间较短,转速和转矩超调较小,且在突加负载过程中,转矩波动较小。该方法提高了控制系统的PID参数在线优化能力,比传统PID控制具有更好的动态特性和鲁棒性,适合应用于高空永磁无刷直流电机螺旋桨负载电驱动系统。
[1] 王强,王友仁,王岭,等.无位置传感器无刷直流电机闭环起动方法[J].电机与控制学报,2013,17(11):42-45
Wang Qiang,Wang Youren,Wang Ling,et al.Closed-Loop Starting Method for Sensorless Brushless DC Motor[J].Electric Machines and Control,2013,17(11):42-45(in Chinese)
[2] 夏长亮,方红伟.永磁无刷直流电机及其控制[J].电工技术学报,2012,27(3):25-34
Xia Changliang,Fang Hongwei.Permanent-Magnet Brushless DC Motor and Its Control[J].Transactions of China Electrotechnical Society,2012,27(3):25-34(in Chinese)
[3] Jinli L,Manfeng D.Fuzzy Adaptive PI Control for Near Space Aircraft Electric Propulsion System[C]//IEEE International Conference on Computer,Mechatronics,Control and Electronic Engineering,2010,4:472-475
[4] Vishal V,Kumar V,Rana K P S,et al.Comparative Study of Some Optimization Techniques Applied to DC Motor Control[C]//IEEE International Conference on Advance Computing,2014:1342-1347
[5] 王裕夫,刘振国,陶国权.某高空螺旋桨气动特性数值模拟与风洞试验[J].北京航空航天大学学报,2013,39(8):1102-1105
Wang Yufu,Liu Zhenguo,Tao Guoquan.Numerical Simulation of High Altitude Propeller′s Aerodynamic Characteristics and Wind Tunnel Test[J].Journal of Beijing University of Aeronautics&Astronautics,2013,39(8):1102-1105(in Chinese)
[6] 雷金莉,窦满峰.高空螺旋桨驱动电机控制系统的仿真研究[J].测控技术,2013,31(12):49-52
Lei Jinli,Dou Manfeng.Simulation Study on Motor Control System Driven High Altitude Airscrew[J].Measurement&Control Technology,2012,31(12):49-52(in Chinese)
[7] 陈声麒,宋笔锋,王海峰.高空飞艇推进系统参数匹配设计[J].西北工业大学学报,2013,31(4):530-534
Chen Shengqi,Song Bifeng,Wang Haifeng.Simulating Parameter Matching for Propulsion System of High Altitude Airship[J]. Journal of Northwestern Polytechnical University,2013,31(4):530-534(in Chinese)
[8] 罗玲,刘卫国,窦满峰,等.高空飞艇螺旋桨驱动电机分析[J].宇航学报,2009,30(6):2140-2144
Luo Ling,Liu Weiguo,Dou Manfeng,et al.Analysis of the Motor Driving a Propeller of High Altitude Airship[J].Journal of Astronautics,2009,30(6):2140-2144(in Chinese)
[9] Gaing Z L,Lin C H,Tsai M H,et al.Rigorous Design and Optimization of Brushless PM Motor Using Response Surface Methodology with Quantum-Behaved PSO Operator[J].IEEE Trans on Magnetics,2014,50(1):1-4
[10]Wai R J,Lee J D,Chuang K L.Real-Time PID Control Strategy for Maglev Transportation System Via Particle Swarm Optimization[J].IEEE Trans on Industrial Electronics,2011,58(2):629-646
[11]Daneshyari M,Yen G G.Constrained Multiple-Swarm Particle Swarm Optimization within a Cultural Framework[J].IEEE Trans on Systems,Man and Cybernetics,Part A:Systems and Humans,2012,42(2):475-490
[12]Li S,Tan M,Tsang I W,et al.A Hybrid PSO-BFGS Strategy for Global Optimization of Multimodal Functions[J].IEEE Trans on Systems,Man,and Cybernetics,Part B:Cybernetics,2011,41(4):1003-1014
A Reset Particle Swarm OPtimization PID Control of Permanent Magnet BLDC Motor for Airscrew Load
Yang Jianwei,Dou Manfeng,Luo Guangzhao,Zhao Dongdong
(Department of Automatic Control,Northwestern Polytechnical University,Xi′an 710072,China)
When permanent magnet brushless DC motor(PMBLDCM)drive high altitude airscrew load,due to the change in atmospheric density with altitude and the frequent fluctuations of airscrew load torque,the traditional given-parameter PID control meets difficulty in the real-time adjustment of the PID parameters of electric power drive systems(EPDS)with environmental change;so the dynamic characteristics and robustness of system is poor.To solve the problem,a novel PID control method based on the BFGS-RPSO algorithm is proposed.The method uses of flexible global and fast local search optimization of BFGS-RPSO algorithm to online optimize the PID parameters of PMBLDCM control system and improve the dynamic characteristics and robustness of electric drive systems with airscrew load.Matlab simulation and experimental results show that the rise time of speed is shorter and the overshoot of speed and torque is less during starting the motor.Besides,the torque ripple is smaller in load fluctuation.The dynamic characteristics and robustness of BFGS-RPSO PID parameter control are better than those of traditional PID control.The method is feasible for the EPDS of PMBLDCM with propeller load.
algorithm,angular velocity,brushless DC motor,controllers,design of experiments,experiments, global optimization,MATLAB,optimization,particle swarm optimization(PSO),permanent magnet, propellers,pulse width modulation,robustness(control systems),three term control systems,torque;airscrew load,BFGS(Broyden-Fletcher-Goldfarb-Shanno),BFGS-RPSO,EPDS(Electric power drive systems),MSR(maximum swarm radius),PMBLDCM
TP351;TP273.2
A
1000-2758(2016)02-0313-08
2015-10-20基金项目:国家自然科学基金(51507143)与陕西省工业科技攻关项目(2015GY090)资助
杨剑威(1986—),西北工业大学博士研究生,主要从事电机控制与电力电子研究。
