基于不确定性信息的空战威胁评估方法

王昱，章卫国，傅莉，黄得刚，何墉

(1.西北工业大学自动化学院，陕西西安 710072；2.沈阳航空航天大学自动化学院，辽宁沈阳 110136)

基于不确定性信息的空战威胁评估方法

王昱1，2，章卫国1，傅莉2，黄得刚1，何墉1

(1.西北工业大学自动化学院，陕西西安 710072；2.沈阳航空航天大学自动化学院，辽宁沈阳 110136)

针对专家先验知识和空战态势信息的不确定性，以证据网络为基本框架，建立了基于敌我双方几何位置关系和运动状态的敌方战机威胁评估模型，首先给出了动态态势信息的信度等级转换及信度值的分配方法，然后针对专家不一致且带有不确定性的属性偏好提出了证据间权重优化方法，最后输入数据，通过网络推理实现敌机威胁等级评估。实例仿真表明，威胁评估模型在不确定性态势信息下能够合理估计敌方单机对已方单机的威胁，证实了模型和方法的有效性。

信息融合；信度等级转换；证据网络；空战威胁评估；不确定性信息；证据权重优化

随着航空电子技术的不断发展，信息化空战已演变成现代空战的重要形式，形成了战机间利用数据链进行作战信息交互，协同完成多目标攻击的网络化协同空战模式。对战场全局态势进行准确判断，发现目标与己方战机之间的相对关系，正确分析并进行威胁评估，掌握己方单机与敌方单机之间的优势和劣势，成为集中优势力量对敌机发动有效攻击，提高杀伤率的关键，为指挥决策提供重要依据。

然而，纷繁复杂的空战态势信息具有极大的不确定性，这种不确定性广泛存在于证据信息的检测环节、专家先验知识以及由此制定的推理规则等各个方面。因此，有针对性地研究不确定性信息的有效处理方法对现代空战具有重要意义。

证据理论集集合论与概率论于一体，适合处理不精确、不完全信息的融合问题［1］，已被广泛应用于处理不确定性态势信息融合［2-4］。而以证据理论为核心的证据网络简化了单纯用Dempster合成规则进行信息间融合的计算复杂度［5］，十分适合对时效性要求很高的空战威胁评估。

本文提出了对不确定性空战态势信息的处理方法，并应用于所构建的基于证据网络的威胁评估模型，实现对敌威胁等级的评估。

1　证据网络及其主要运算

证据网络(evidential network，EN)是由网络结构和网络参数组成的有向无环图，其核心运算是DS证据理论中的Dempster合成规则，融合了图论与证据理论，是定性与定量方法的有机结合。

文献［5］给出了定义于VBS(Valuation-based system)图模型框架下的EN，表示为五元组形式｛V，ΘV，MV，⊕，↓｝，其中V表示模型所有变量的集合，ΘV为所有变量的识别框架集合，MV为变量间评价函数(也即信度关系)的集合，⊕为合成算子、↓为消元算子。

应用EN进行数据融合首先需结合知识库及专家的先验知识构建网络结构和评价函数，然后进行网络推理：将信度结构表示的节点证据输入EN，将模型中的变量依序进行合成(⊕)运算，逐步消除间接变量，最终获取所关心的决策变量的信度值。其推理过程中的主要运算有：

1)合成运算(⊕)

对定义于相同的变量子集上的信度合成方使用Dempster合成规则。假设基本信度分配(basic belief assignment，BBA)定义于变量集d(m1)＝

2)扩展运算(↑)

对定义于不同的变量子集上的信度合成方(D1≠D2)，需要将待合成方的BBAs分别扩展到变量合集D1∪D2，再应用(1)式进行信度合成运算。即

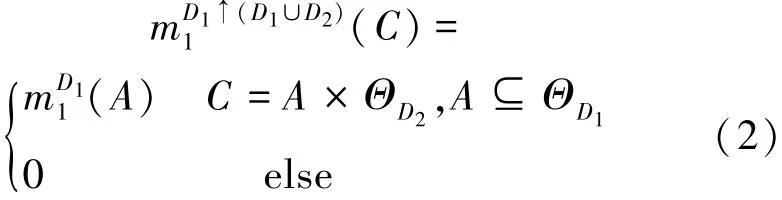
3)边际化运算(↓)

通过将BBAs分配到缩小的变量集合中，消除某些不需要的变量。假设原变量集合为D，边际化后的变量集合为D′⊆D。边际化操作可表示为

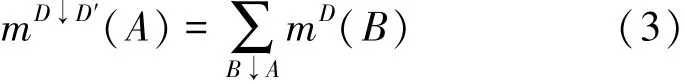
式中，A⊆ΘD′，B⊆ΘD。

经(1)～(3)式运算后EN网络推理的结果为信度测度形式，难以直接用于决策，需要用Pignistic变换将其转换为概率测度。设mD为定义在变量子集D上的BBAs，ΘD为D的识别框架集合，则对ΘD中的任意元素θi，其概率测度计算如下

为便于比较威胁评估结果，在(4)式的基础上可进一步计算变量等级的数学期望

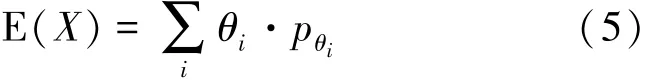
X为定义于ΘD上的变量。

2　态势优势计算及其信度结构转化

本文选择与空战威胁评估密切相关的角度优势、距离优势、速度优势、高度优势作为威胁评估主要因素。

2.1态势优势计算

按照文献［6-7］对敌方各动态态势优势的计算方法，确定蓝(敌)方i机对红(我)方j机的优势函数计算如下：

式中，Δhij为蓝方i机与红方j机间的高度差。

2.2不确定性证据信度结构转换

2.2.1信度等级转换

由公式(6)～(9)计算出的敌机各态势优势的定量信息均在［0，1］内，而本文建立的节点信息评价等级为｛0，1，2｝，故可将计算出的各优势信息按照所属区间统一转化至相邻的2个评价等级上，并进行相应的信度分配，如图1所示。

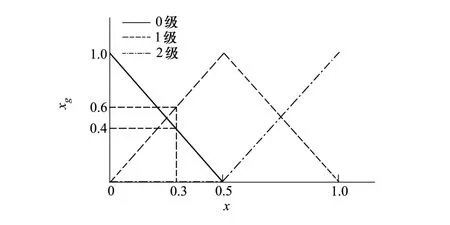
图1　证据信度等级转换及信度分配曲线

例如，若计算出的态势优势x＝0.3，可分配至0级和1级，信度转换为：｛0｝：0.4；｛1｝：0.6。

2.2.2不确定性处理

考虑信息具有不确定性，对信息做不确定性处理，设信息x经等级转换映射至a、b级(a，b＝0，1， 2，且a、b相邻)，在各级上的信度分配由图1计算为xag、xbg。设对该信息的不确定因子为ρ，则新的信度分配如表1所示：

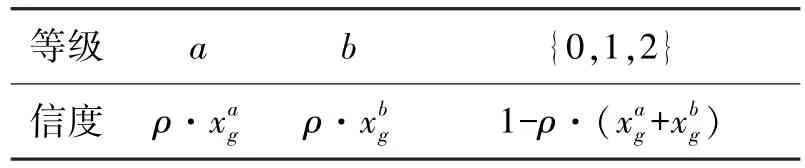
表1　不确定信息的信度分配

本文将检测到的证据信息经公式(6)～(9)计算，信度结构转换处理后输入EN网络再进行威胁等级评估。

3　基于不确定偏好关系的节点权重确定

证据网络中，当父节点是由其子节点的加和关系确定时，需要确定各子节点的权重。在信息具有一定不确定性的前提下，如何获取各子节点的权重显得十分重要。针对此问题，本文提出基于不确定偏好关系的节点权重优化方法。

借鉴多属性决策中属性权重的给定方法，网络节点的重要程度可以通过专家对两两变量给出的偏好关系的形式给出。

设X＝｛x1，x2，…，xn｝ (n≥2)是一组需要给出权重的节点。W＝｛w1，w2，…，wn｝为待确定的各变量权重。设第k(k＝1，2，…，K)个专家对该组节点的重要程度进行评判，以表2形式给出：

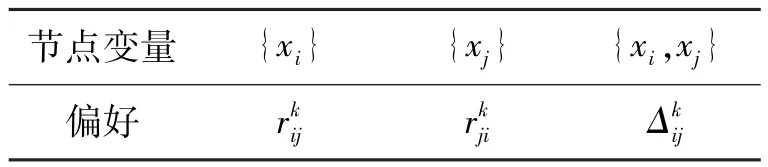
表2　第k个专家的节点偏好

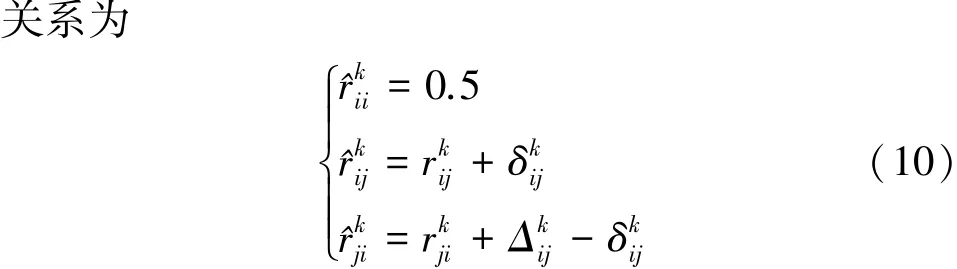
完成对所有变量两两偏好比较关系后，可建立对所有节点x1，x2，…，xn的评判关系矩阵：

采用优化算法对此模型求解，即可得到所需的节点权重。

4　威胁评估EN网络模型构建

本文以几何位置与运动态势为核心因素构建了威胁评估EN模型，如图2所示。

图2　威胁评估EN模型

图中6个变量用圈表示，信度函数用菱形表示，变量的说明如表3所示。

为便于合成，将图2的威胁估计模型转化为二值联合树形式，如图3所示。

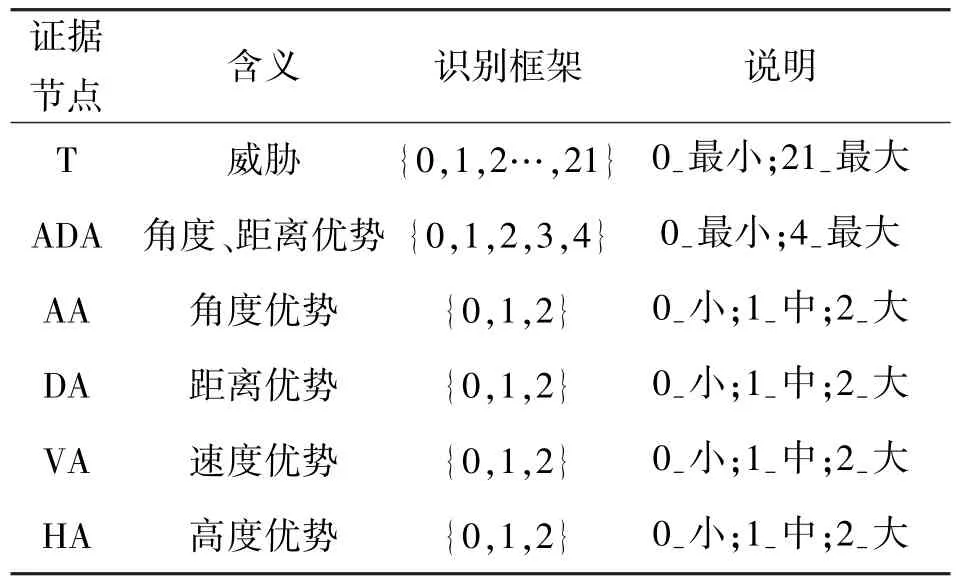
表3　态势估计EN模型的变量说明

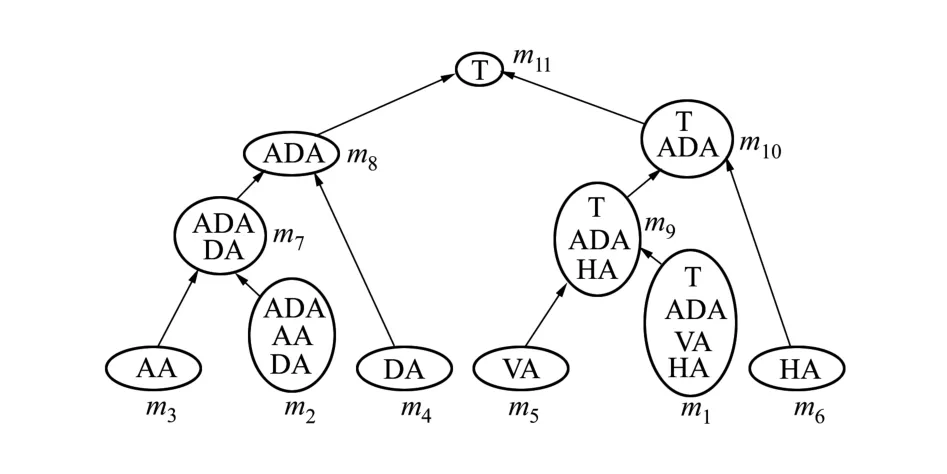
图3　基于EN的威胁评估二值联合树模型

需要说明的是，威胁T的识别框架是经过节点ADA、VA、HA权重确定及等级整数化处理的结果，具体见仿真实例。

网络构建好后，为检测网络结构、信度分配和推理效果，应进行网络运行结果测试。本文选用3种特殊证据作为网络输入——最低威胁、最高威胁以及完全不确定输入，即各证据输入信度分别在最低威胁、最高威胁和整个识别框架等级处取1，其余取0，输入网络。测试结果在仿真算例中参数给定后给出。

5　仿真算例

设空战红、蓝方各派出2架战机，各战机的具体指标如表4、5所示。专家给出的节点偏好关系如表6。各态势信息的不确定性因子如表7所示。

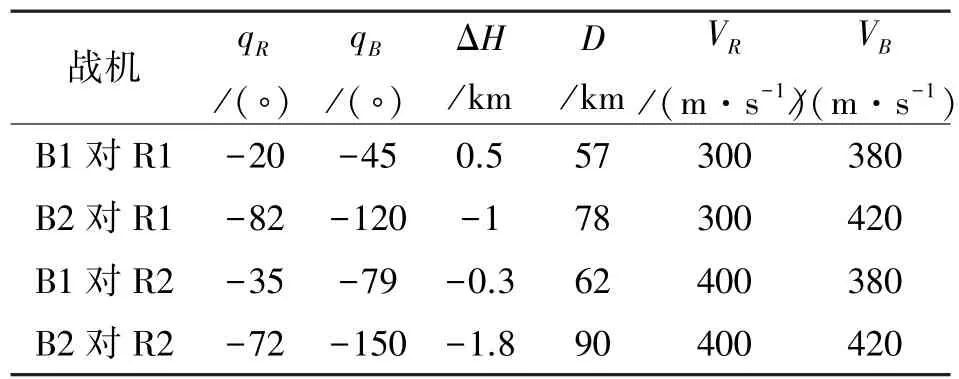
表4　蓝方各战机对红方各战机的空战态势参数

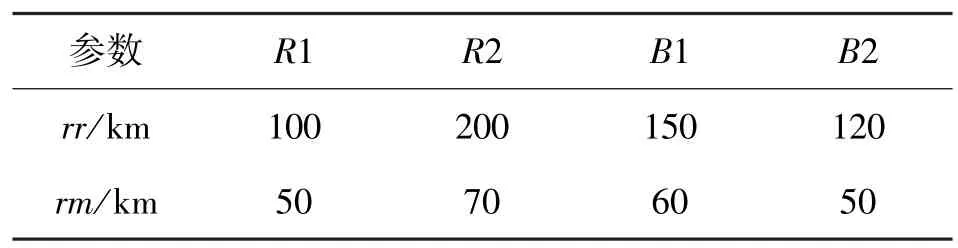
表5　红、蓝方各战机空战能力参数

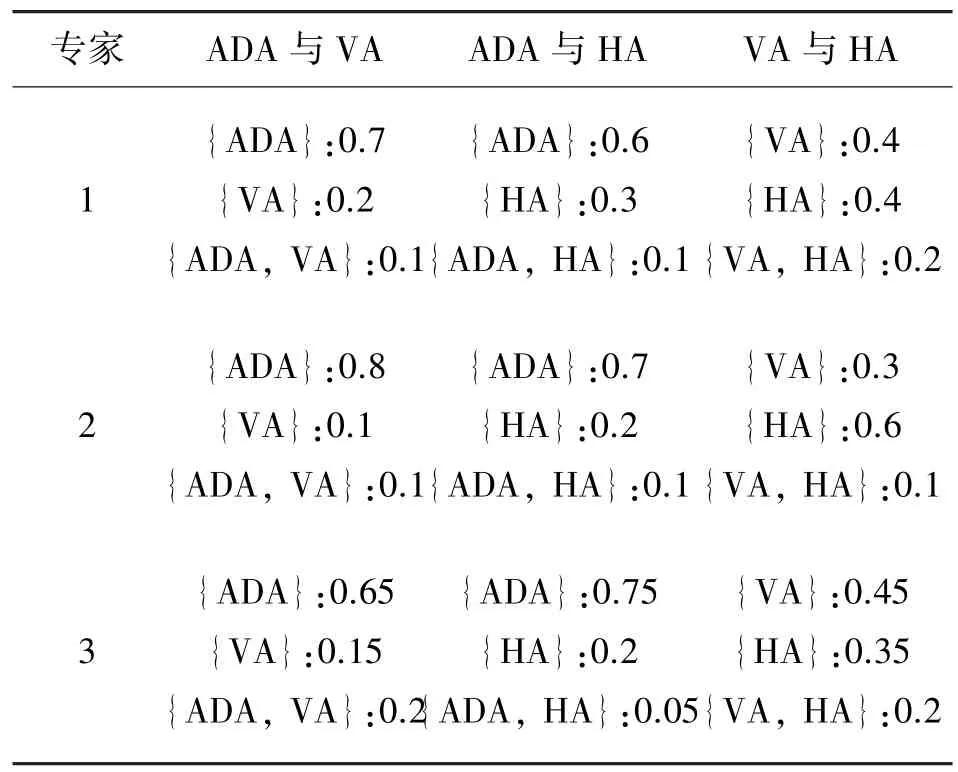
表6　专家给出的节点变量偏好关系

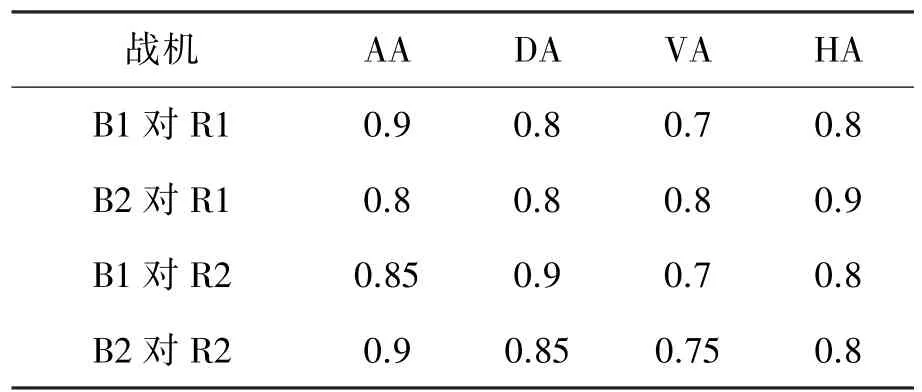
表7　各优势信息不确定性因子

5.1节点ADA、VA、DA权重确定

按照前文中的权重确定方法，输入表6中的专家偏好信息，应用粒子群方法对(11)式进行优化，获取的权重分配结果为：wADA：0.630 0；wVA：0.157 5；wHA：0.212 5。

5.2m1和m2的变量关系确定

考虑实际空战中距离优势与角度具有较强的耦合性［8］，确定m2为乘积关系，应用规则ADA＝AA× DA，由变量范围分配m2：m2｛(0，0，0)，(0，0，1)，…，(4，2，2)｝＝1，共9个元素。

考虑实际空战中角度距离优势、速度优势及高度优势相对独立，依照表计算出的权重分配，确定节点m1为如下的加和关系：应用规则T＝4×ADA＋VA＋1.35×HA，由变量范围分m1：m1｛(0，0，0，0)， (4，4，0，0)，…，(20.7，16，2，2.7)｝＝1，共45个元素。

5.3应用EN进行敌机威胁评估

1)网络测试

将5.2中确定的m1和m2输入网络测试。结果如图4所示。应用公式(5)计算出各情况下威胁期望在低威胁处取得最小值0，高威胁处取得最大值20.7，完全不确定情况下取得近中间值，因此网络结构和参数合理。

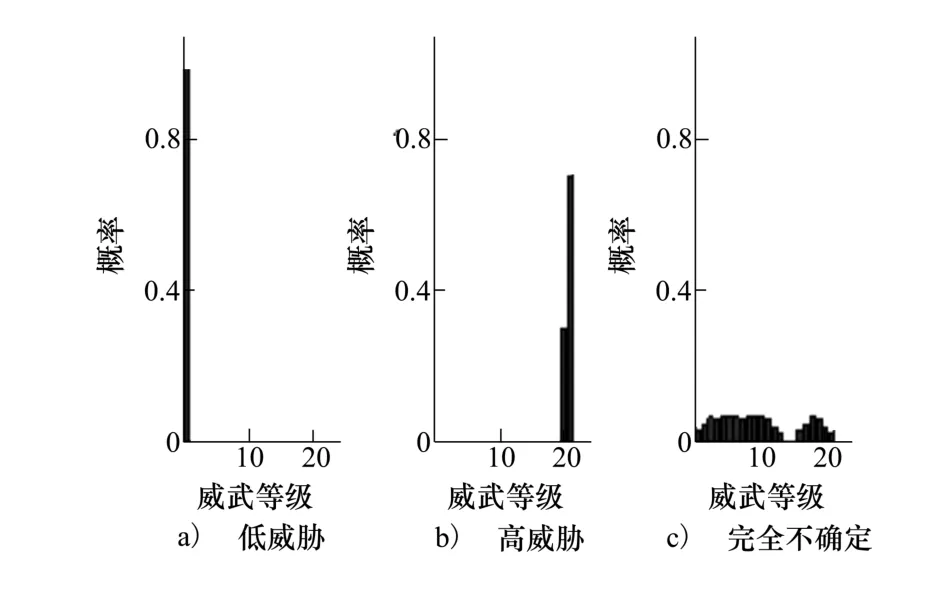
图4　网络测试结果

2)实际数据输入

①不考虑态势信息不确定性

将表4、表5中的数据输入公式(6)～(9)，再经过信度等级转换(不进行不确定性处理)，输入本文构建的威胁评估EN网络。运行结果如图5所示。

这里需要说明的是由于各证据节点的权重非全为整数，因此威胁等级也非完全为整数级，文章采用类似前文信度等级转换的方法将非整数级威胁信度转化至相邻两整数级，共分为22级：0～21。

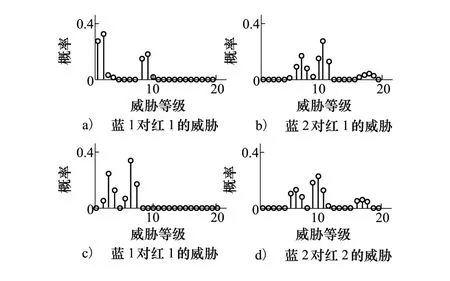
图5　不考虑态势信息不确定性的威胁评估结果

②考虑态势信息不确定性

按照表7的不确定性因子进行数据的不确定性处理后再输入EN网络进行各战机威胁评估，评估结果如图6所示。

比较图5和图6，可以看出威胁值在不同等级上的概率分布随着输入信息的不确定性发生波动性改变。将直接由公式(6)～(9)计算的数据采用加权合成公式T＝4·AA·DA＋VA＋1.35·HA计算，与上述2种情况的计算结果进行比较，列于表8。

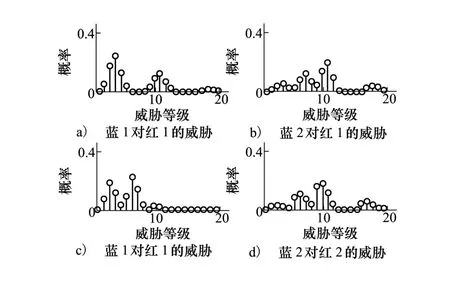
图6　考虑态势信息不确定性的威胁评估结果

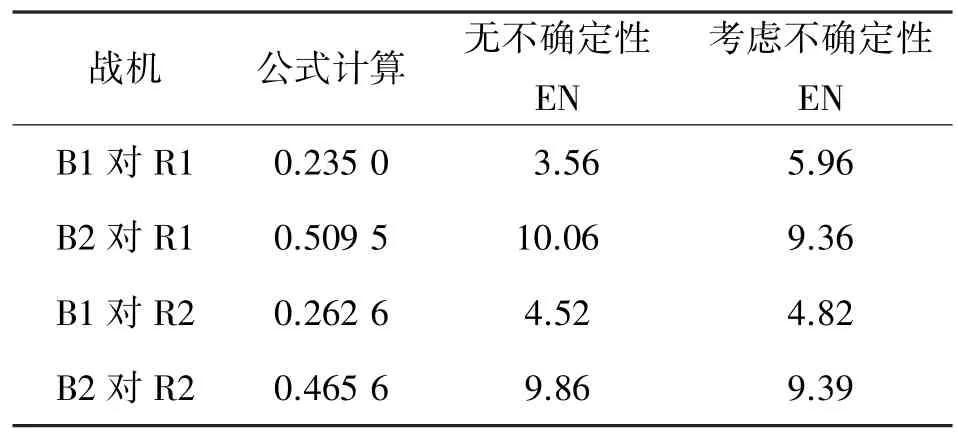
表8　各种情况威胁评估结果比较

由表8可见，若不考虑不确定性信息因子，EN推理得到的威胁排序结果与公式计算结果相同，均为：B2对R1＞B2对R2＞B1对R2＞B1对R1，说明了网络推理的正确性。考虑信息不确定性后，威胁排序结果发生改变：B2对R2的威胁大于B2对R1。同时在考虑信息不确定性的情况下采用文献［9］的基于IFF动态直觉模糊法对仿真算例的目标威胁进行了评估计算，得出结论：B2对R1＞B1对R1；B2对R2＞B1对R2，在考虑单机所受目标威胁的情况下与本文结论一致，同样证实了本文方法的有效性，然而该方法未能进行多机间的威胁排序比较，难以适用于无人机间协同作战决策。

6　结 论

本文以基于VBS的证据网络为基本框架，以敌我双方战机的几何位置关系和运动状态为节点变量，构建了敌方单机对我方单机的威胁评估模型。提出了不确定性动态信息的信度结构转换方法和针对专家不确定性属性偏好的节点权重优化方法。通过实例仿真证明了本文构建的威胁评估模型以及提出的不确定信息处理方法的合理性和有效性，同时说明了进一步考虑态势信息的不确定性可能使敌机威胁顺序发生改变，对后续空战决策将起到一定的参考作用。

［1］ 姜江.证据网络建模、推理及学习方法研究［D］.长沙：国防科技大学，2011

Jiang Jiang.Modeling、Reasoning and Learning Approach to Evidential Network［D］.Changsha，National University of Defense Technology，2011(in Chinese)

［2］ 邓勇，朱振福，钟山.基于证据理论的模糊信息融合及其在目标识别中的应用［J］.航空学报，2005，26(6)：754-758

Deng Yong，Zhu Zhenfu，Zhong Shan.Fuzzy Information Fusion Based on Evidence Theory and Its Application in Target Recognition［J］.Acta Aeronautica et Astronautica Sinica，2005，26(6)：754-758(in Chinese)

［3］ Huang S，Su X，Hu Y，et al.A New Decision-Making Method by Incomplete Preferences Based on Evidence Distance［J］. Knowledge-Based Systems，2014，56：264-272

［4］ Rohitha K K，Hewawasam G K，Kamal Premaratne.Rule Mining and Classification in a Situation Assessment Application：A Belief-Theoretic Approach for Handling Data Imperfections［J］.IEEE Trans on Systems，Man，and Cybernetics，2007，37(6)：1447-1459

［5］ Benavoli A，Ristic B，Farina A，et al.An Application of Evidential Networks to Threat Assessment［J］.IEEE Trans on Aerospace and Electronic Systems，2009，45(2)：620-639

［6］ 张堃，周德云.基于熵的TOPSIS法空战多目标威胁评估［J］.系统工程与电子技术，2007，29(9)：1493-1495

Zhang Kun，Zhou Deyun.TOPSIS Method Based on Entropy in Evaluating the Air Multi-Target Threat［J］.Systems Engineering and Electronics，2007，29(9)：1493-1495(in Chinese)

［7］ 肖亮，黄俊，徐钟书.基于空域划分的超视距空战态势威胁评估［J］.北京航空航天大学学报，2013，39(10)：1309-1313

Xiao Liang，Huang Jun，Xu Zhongshu.Modeling Air Combat Situation Assessment Based on Combat Area Division［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39(10)：1309-1313(in Chinese)

［8］ 吴文海，周思羽，高丽，等.基于导弹攻击区的超视距空战态势评估改进［J］.系统工程与电子技术，2011，12(33)：2679-2684

Wu Wenhai，Zhou Siyu，Gao Li，et al.Improvements of Situation Assessment for Beyond-Visual-Range Air Combat Based on Missile Launching Envelope Analysis［J］.Systems Engineering and Electronics，2011，33(12)：2679-2684(in Chinese)

［9］ 张堃，王雪，张才坤，等.基于IFE动态直觉模糊法的空战目标威胁评估［J］.系统工程与电子技术，2014，36(4)：697-701

Zhang Kun，Wang Xue，Zhang Caikun，et al.Evaluating and Sequencing of Air Target Threat Based on IFE and Dynamic Intuitionistic Fuzzy Sets［J］.Systems Engineering and Electronics，2014，36(4)：697-701(in Chinese)

A Method of Threat Assessment for Aerial Combat Using Uncertain Information

Wang Yu1，2，Zhang Weiguo1，Fu Li2，Huang Degang1，He Yong1

(1.Department of Automatic Control，Northwestern Polytechnical University，Xi′an 710072，China
2.School of Automation，Shenyang Aerospace University，Shenyang 110136，China)

Aiming at the uncertainty of expert knowledge and situation information in aerial combat，we establish a threat assessment model based on evidence network.The geometric location relation and movement states of both sides of fighting are the two main factors considered in the model.First，the belief level conversion method and that of belief value distribution are given.Then，according to the inconsistent and uncertain attribute preference from experts，a weight optimization method between evidence is put forward.Finally，the threat level assessment of enemy aircraft is realized by network reasoning through the inputting data.The simulation results show that the threat of each enemy aircraft toward each of our aircraft is reasonably evaluated with uncertain situation information. Therefore the validity of our method，including that of the model，is verified.

belief level conversion，evidence network，threat assessment for aerial combat，uncertain information， weight optimization between evidence

V271.4；TP181

A

1000-2758(2016)02-0299-07

2015-03-24

国家自然科学基金(61374032)、辽宁省教育厅科学研究一般项目(L2015412)与航空科学基金(2012ZA01011)资助

王昱(1980—)，女，西北工业大学博士研究生，主要从事无人机空战态势估计及目标分配的研究。