基于随机矩阵的新型频谱盲感知方法

刘宁，史浩山，刘利平，杨博

(1.西北工业大学无人机特种技术重点实验室，陕西西安 710065

2.西北工业大学电子信息学院，陕西西安 710072；3.中兴西安研究所，陕西西安 710065)

基于随机矩阵的新型频谱盲感知方法

刘宁1，2，史浩山2，刘利平3，杨博1

(1.西北工业大学无人机特种技术重点实验室，陕西西安 710065

2.西北工业大学电子信息学院，陕西西安 710072；3.中兴西安研究所，陕西西安 710065)

针对传统频谱感知算法需要预先估计噪声方差且当存在噪声不确定度时，检测性能降低的特点，提出一种基于随机矩阵的改进型频谱盲感知算法（M-CMME）。该算法通过分析协方差矩阵最大特征值极限分布特性，分析并利用采样协方差矩阵特征值与信号平均能量的关系，推导设定虚警概率条件下判决门限的闭式表达式。该算法不需要预先知道授权用户信号的先验知识，且能够有效克服噪声不确定度的影响。仿真结果显示，当噪声方差估计存在偏差的情况下，该算法具有较强的鲁棒性，且在较少采样点、低信噪比、较少阵元数情况下能够获得比CMME更优的检测性能。

频谱感知；特征值；噪声不确定度；随机矩阵理论

随着无线通信技术的快速发展，频谱资源作为一种不可再生资源，频谱短缺问题日益显现，然而频谱短缺并不是真正意义上的短缺，而是频谱资源没有充分利用的结果。认知无线电［1］技术作为一种新型解决方法受到日益重视。认知无线电核心思想是在不影响主用户工作的前提下，尽可能的充分利用空闲频段。认知无线电的第一步是频谱感知，能量感知算法［2］作为运算简单且不需要授权用户(PU)发射信号信息和信道情况而应用广泛，但该算法的缺点是需要预先知道噪声方差。

近年来，利用随机矩阵理论(RMT)实现频谱感知迅速成为研究热点［3-8］。文献［3］提出LSC合作频谱感知算法，该方法基于大维RMT理论，以采样协方差矩阵最大特征值和最小特征值的极限值之比作为判决门限。该算法能够在无需任何有关PU发射机信号的先验知识的条件下获得比传统能量感知ED算法更好的检测性能。但是该算法在采样数较少的实际应用情形下性能不够理想并且该判决门限无法根据实际情况动态调整，影响算法的感知性能及可靠性。文献［4］提出了一种基于RMT的MED算法，该方法克服文献［3］算法中判决门限固定不变的缺点，根据采样协方差矩阵最大特征值近似分布函数获得能够根据预先设定虚警概率动态调整的判决门限，但该算法同样需要预先估计噪声功率。文献［5］提出一种基于最小特征值的合作频谱感知方法，利用采样协方差矩阵最小特征值的概率密度函数获取判决门限。当不存在噪声不确定度，文献［4-5］算法在某特定环境下具有比ED算法优越的性能，但是在噪声不确定存在环境和ED算法一样容易受到噪声不确定度的影响。文献［6-7］提出最大最小特征值算法(maximum-minimum eigenvalue detection，MME)，基于最大特征值的分布特性并结合最小特征值的极限值使得在不需要预先知道噪声功率的情况下优化系统感知性能，但该算法是将单节点采样数据经过窗口平滑构建采样协方差矩阵，是一种非协作感知算法。文献［8］提出一种协作感知算法(CMME)，是一种通过多节点共享数据构建采样协方差矩阵的MME算法，改善了系统感知性能。但是采用多节点实现协作感知需要分配额外的通信信道实现数据交换。文献［6-8］中提及的MME算法或CMME算法均是利用最大最小特征值实现频谱感知，没有充分考虑采样协方差矩阵所有特征值包含的能量信息对感知结果的影响。因此，本文基于多天线技术构建采样协方差矩阵，通过分析采样协方差矩阵最大特征值的极限分布特性，结合信号平均能量与协方差矩阵特征值之间关系，实现一种改进的M-CMME算法。

1　系统模型

为了不失一般性，假设认知用户是由M个等间距为d的天线组成的均匀阵列天线，信号入射角度相对于法向阵列方向为θ。认为远场信号的入射波达到天线阵列时为平行波。噪声服从均值为0，方差为σ2的高斯分布，且噪声和信号之间分别独立且互不相干。对认知用户阵列天线接收到的信号表示为

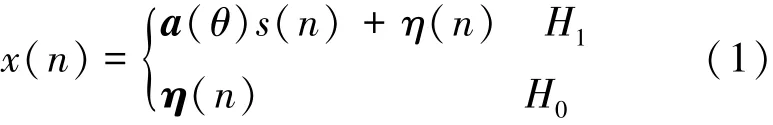
式中，s(n)为认知用户第n时刻接收到的主用户信号，a(θ)＝［1，e－jϕ，e－2jϕ，…，e－(M－1)jϕ］T，ϕ＝2πdsinθ/λ为均匀线阵的导向向量，λ为主用户信号的载波波长，η(n)＝［η1(n)，η2(n)，η3(n)，…，ηM(n)］T为噪声向量，ηi(n)，i＝1，2，…，M为认知用户第i根天线在第n时刻接收到的噪声信号，T表示转置。对每一个认知节点进行N次采样，采样数据可以构成一个M×N维矩阵，表示如下

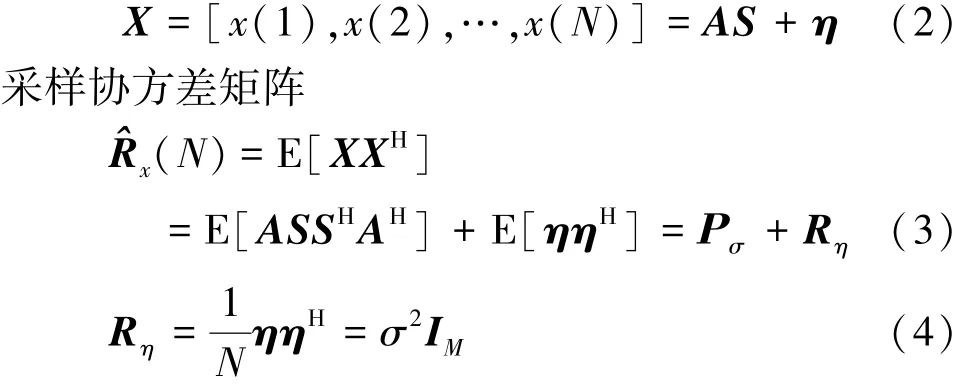
IM为M阶单位矩阵，当PU信号不存在的情况下，采样协方差矩阵由噪声方差组成的对角线矩阵，H表示共轭转置。

2　基于随机矩阵的频谱盲感知

2.1检测统计量分析

λi＝ρi＋σ2。当阵列天线由M个阵元进行N采样，其平均能量为

可以推导出［5］

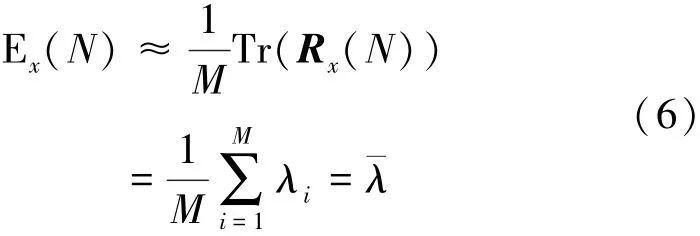
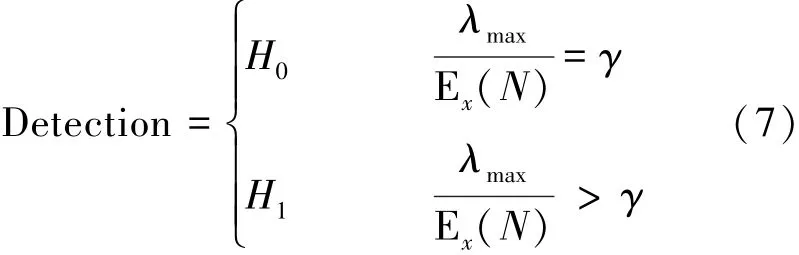
2.2判决门限的理论分析

虚警概率(Pf)可以反映认知无线电对频谱的利用率，虚警概率越高频谱利用率越低，检测概率(Pd)反映认知无线电对授权用户的干扰水平，检测概率越高，对授权用户的干扰越小。在低信噪比环境下，无法预先知道PU发射机信号是否存在，因此根据Pd去推导判决门限相对困难。因此常常通过定义Pf来推导判决门限，即所谓的恒虚警概率准则(CFAR)。近年来随机矩阵理论的研究成果表明，当PU发射机信号不存在时，噪声协方差矩阵n(N)属于Wishart随机矩阵［9］。当PU信号不存在，Marcenko和Pasture发现当Wishart矩阵满足某

研究学者除了对特征值的极限值进行研究外，对特征值的分布情况也进行了深入研究。其中Johnstone和Johansson分别在2000年和2001年对Wishart随机矩阵最大特征值的分布情况进行了研究［10⁃11］，并得出结论：

式中，q(u)是下列PainleveΠ非线性微分方程的解q″(u)＝uq(u)＋2q3(u)。

从公式(8)可以看出，求取一阶Tracy-Widom累计分布函数的解析解表达式是相当困难的。幸运的是Johnstone在文献［10］中计算出一阶Tracy-Widom累计分布函数的一些离散值，并制成了一张表格，如表1所示，根据这张表格，我们能通过查表计算某些离散点上一阶Tracy-Widom分布函数值F1(t)。

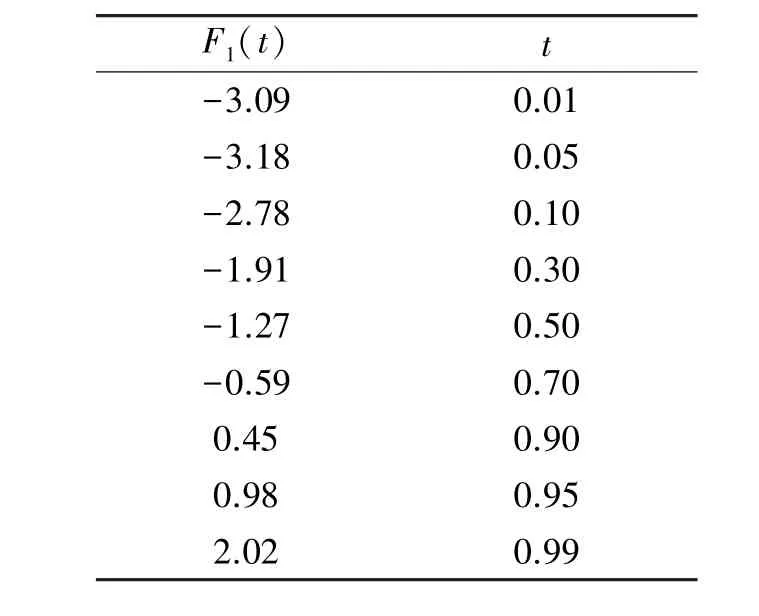
表1　一阶Tracy-Widom累计分布函数离散值

本算法正是基于特征值的分布特性展开研究。从公式(8)及定理1可以得到，当噪声为实信号时，本文对判决门限进行推导如下：

得到MDE算法的判决门限为

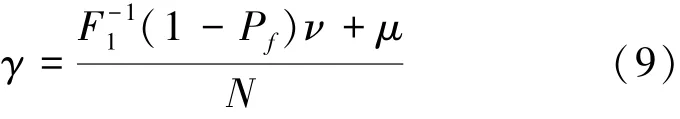
根据事先设定的Pf值，通过查表1即可求出参数γ。当噪声为复信号时，依据定理2，将F1(t)换成2阶Tracy-Widom累计分布函数F2(t)，并按上述推导过程即可求出参数γ。从公式(9)可以看出，判决门限γ的设置只和N、M和Pf设定值有关，与噪声强度无关，因此M-CMME算法不受噪声不确定度的影响，具有较好的检测性能。

2.3检测步骤

1)接收M个阵元经过N次采样数据，组成采样数据矩阵X；

3)求采样协方差矩阵的最大特征值λmax；

4)计算采样数据计算接收信号的平均能量Ex(N)；

5)根据预先设定的虚警概率根据公式(9)求取判决门限γ；

6)根据算法的判决准则公式(8)进行结果判决，当λmax/Ex(N)＞γ，判决H1成立。反之λmax/Ex(N)≤γ时，判决H0成立即无主信号存在。

3　性能仿真及分析

本文借助Matlab仿真平台进行1 000次Monte Carlo模拟仿真并且采用恒虚警概率准则比较ED， M-CMME，CMME算法的感知性能。考虑到噪声不确定性的影响，假设仿真噪声方差为σ2，噪声不确定度为ρ dB，则估计的噪声方差为＾σ2＝ (10x/10δ2)σ2，其中，x∈(－ρ，ρ)。

为了测试不同的信噪比条件下，噪声不确定度对各算法的影响，这里假定Pf＝0.1，对8元均匀线性阵列进行2 000次采用，为了体现低信噪比，信噪比从－20 dB到－10 dB变化。在仿真曲线中，ED－0 dB，ED－1 dB，ED－2 dB分别表示噪声不确定性为0 dB、1 dB、2 dB时ED算法的检测性能。仿真结果如图1所示。从结果图中可以看出当噪声不确定度为0，即噪声功率能够被精确估计时，在较低信噪比时， ED算法优于M-CMME算法和CMME算法，随着信噪比的提高，M-CMME和CMME算法性能较ED算法明显提高。当噪声不确定度存在时，ED算法明显受到估计噪声方差的影响，性能改变较大且明显差于M-CMME和CMME算法，并且在任意的信噪比条件下M-CMME性能都优于CMME算法。

为了进一步比较各算法检测性能，在假设信噪比固定为－16 dB，Pf＝0.1条件下将数据采样点分别以500点为步进从1 000点累加至9 000点，噪声不确定性分别为0 dB、1 dB和2 dB进行仿真。

从图2可以看出，随着采样点的增多，在噪声估计准确的情况下，ED算法在一定的虚警概率条件下，随着采样点数的增多，检测概率逐渐增大，但是当噪声不确定度存在时，随着采样点数的增多，ED算法检测性能变化不大。这也就说明噪声不确定度问题并不能仅仅通过增加采样点数而得到解决。而M-CMME和CMME算法并没有受到噪声不确定度的影响，随着采样点的增加算法能够达到完全检测的目的，而在同样的采样点M-CMME算法始终具有比CMME更高的检测概率。

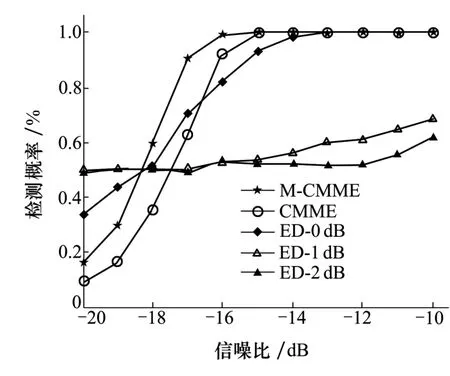
图1　噪声不确定条件下算法性能比较

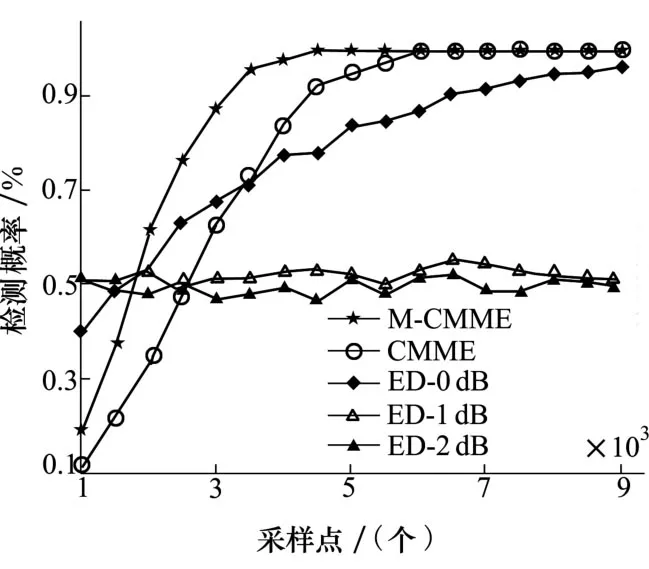
图2　采样点对算法性能的影响

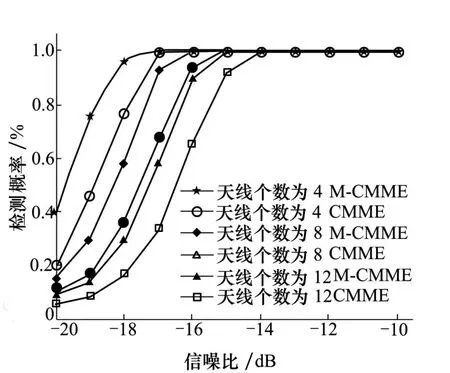
图3　天线数量对算法性能影响

当天线阵的阵元数加大，意味着每一次采样的数据量加大，在弱信号环境下，信号能量也加大，噪声不发生改变，因此，理论上，检测概率应该会提升。在同样的仿真条件下，阵元个数分别为M＝6、M＝8、M＝12对算法进行验证。

从仿真图中可以看出，随着阵元个数的增加， M-CMME和CMME检测性能明显增加。阵元数等于6，检测概率最低，而阵元数等于12时，检测概率相对更好，且M-CMME比CMME具有更好的检测效果。通过对3种仿真条件下不同算法之间的比较可以看出，M-CMME算法不受到噪声不确定度的影响，且其检测性能明显均优于CMME算法。

4　结 论

本文基于阵列天线技术，利用随机矩阵理论及采样协方差矩阵特征值具有的能量特性，提出一种改进型盲频谱感知算法(M-CMME)。理论分析表明，该方法的判决门限仅由采样点、阵列天线阵元数及虚警概率动态调整，和噪声方差无关。通过对该算法仿真验证结果表明：该算法对噪声不确定性具有较好的鲁棒性，且能够在低采样点、低信噪比、低阵元数环境下，获得较好的检测性能。

［1］ Mitola J，Maguire G Q.Cognitive Radios：Making Software Radios More Personal［J］.IEEE Personal Communications，1999，6 (4)：13-18

［2］ Digham F F，Alouini M S，Simon M K.On the Energy Detection of Unknown Signals over Fading Channels［J］.IEEE Trans on Wireless Communication，2007，55(1)：21-24

［3］ Cardoso L S，Debbah M，Bianchi P，et al.Cooperative Spectrum Sensing Using Random Matrix Theory［C］//International Symposium on Wireless Pervasive Computing，Santorini，2008：334-338

［4］ Zeng Y H，Koh C L，Liang Y CH.Maximum Eigenvalue Detection：Theory and Application［C］//IEEE International Conference on Communications，Beijing，2008：4160-4164

［5］ 曹开田，杨震.基于最小特征值的合作频谱感知新算法［J］.仪器仪表学报，2011，32(4)：736-741

Cao Kaitian，Yang Zhen.Novel Cooperative Spectrum Sensing Algorithm Based on the Smallest Eigenvalue［J］.Chinese Journal of Scientific Instrument，2011，32(4)：736-741(in Chinese)

［6］ Zeng Yonghong，Liang Yingchang.Eigenvalue-Based Spectrum Sensing Algorithms for Cognitive Radio［J］.IEEE Trans on Communications，2009，57(6)：1784-1793

［7］ Zeng Yonghong，Liang Yingchang.Maximum-Minimum Eigenvalue Detection for Cognitiv Radio［C］//The 18thAnnual IEEE International Symposium on Personal，Indoor and Mobile Radio Communications，2007：1-5

［8］ 王磊，郑宝玉，李雷.基于随机矩阵的协作频谱感知［J］.电子与信息学报，2009，31(8)：1925-1929

Wang Lei，Zheng Baoyu，Li Lei.Cooperative Spectrum Sensing Based on Random Matrix Theory［J］.Journal of Electronocs＆Information Technolgy，2009，31(8)：1925-1929(in Chinese)

［9］ Tulino A M，Verdu S.Random Matrix Theory and Wireless Communications［M］.Hanover，USA：Now Publisher Inc，2004：3-73

［10］By Iain M.Johnstone On the Distribution of the Largest Eigenvalue in Principle Components Analysis［J］.Annals Statistics， 2001，29(2)：295-327

［11］Johansson K.Shape Fluctuations and Random Matrices［J］.Commun Math Phys，2000，209(2)：437-476

A Novel Blind SPectrum Sensing Algorithm Based on Random Matrix

Liu Ning1，2，Shi Haoshan2，Liu Liping3，Yang Bo1
(1.Science and Technology on UAV Laboratory，Northwestern Polytechnical University，Xi′an 710065，China
2.Department of Electronics and Engineering，Northwestern Polytechnical University，Xi′an 710072，China
3.Xi′an Institute of ZTE，Xi′an 710065，China)

In order to improve the detection performance of traditional spectrum sensing under low SNR，a spectrum sensing algorithm(M-CMME)is proposed.The proposed algorithm analyzes the characteristic of limiting eigenvalue distribution，analyzes and utilizes the relation of energy and eigenvalues of sample matrix and then deduces the form expression of decision threshold under constant false alarm ratio.The algorithm，we believe，does not need estimating the noise power and exhibits a good robustness against noise uncertainty.Simulation results show preliminarily that，when there is a deviation of the noise estimation，the algorithm can obtain strong robustness and this algorithm can get better detection performance than CMME with fewer samples，lower SNR and fewer antennas.

algorithm，antenna array，computer simulation，covariance matrix，eigenvalues and eigen functions， estimation，matrix algebra，Matlab，Monte Carlo methods，wavelength；blind spectrum sensing，Constant false alarm ratio，CMME，CDF(cumulative distribution function)，ED，MDE，MME(maxim minimum eigenvalue detection)，PU，RMT(random matrix theory)，Wishart random matrix

TN92

A

1000-2758(2016)02-0262-06

2015-10-20

2012航天科技支撑基金(2012HTXGD)与西北工业大学基础研究基金(3102014KYJD014)资助

刘宁(1976—)，女，西北工业大学工程师、博士研究生，主要从事通信工程与信号处理、数据链仿真及电磁兼容环境适应性技术研究。