水声MIMO-OFDM通信中的空频迭代信道估计与均衡
2016-10-29张玲玲黄建国韩晶张群飞
张玲玲,黄建国,韩晶,张群飞
(西北工业大学航海学院,陕西西安 710072)
水声MIMO-OFDM通信中的空频迭代信道估计与均衡
张玲玲,黄建国,韩晶,张群飞
(西北工业大学航海学院,陕西西安 710072)
在MIMO-OFDM水声通信系统中,由于信道间的相互干扰和水声信道严重时延扩展产生的频率选择性衰落,系统的通信误码率较高。针对这一问题,研究了空频编码的MIMO-OFDM通信,提出空频迭代信道估计与均衡(Spatial Frequency Iterative Channel Estimation and Equalization,SFICEE)方法。该方法通过载波间的空频正交性进行各收发阵元对的信道估计,并通过空频均衡获得符号初始估计,迭代更新信道估计,而后通过符号后验软信息反馈进行迭代空频软均衡。仿真结果表明,当误码率为10-3时,文中所提出的SFICEE方法经过二次迭代与STBC方法相比具有4.8 dB的性能增益,相对于SFBC方法有2.8 dB的性能提升。当输入信噪比相同时,文中所提出方法的星座图更加收敛,可以更好地降低水下通信系统的误码率。
水下通信;多输入多输出;正交频分复用;空频软均衡;迭代信道估计
近年来随着海洋勘探和海底测绘等海洋水下应用需求的增加,水下通信技术逐渐成为通信领域的研究热点之一。水声通信是水下无线通信的主要方式,然而水声信道多径效应较为严重,导致码间干扰较大,对水下通信系统提出很高的要求[1]。由于水声通信收发平台的高移动性和水声环境的波动性,导致水下信道的时变特性较强[2];此外,由于水下声速很低,导致其时间变化率远远大于无线信道[3]。近年来,正交频分复用(Orthogonal Frequency Domain Multiplexing,OFDM)技术由于抗多径性能较好,被广泛应用于水下通信系统[4-5]。然而,OFDM信号的峰均功率比(Peak to Average Power Ratio, PAPR)较高[6],受水声换能器发射功率限制,水听器端信噪比较低,导致系统吞吐量受限。为此,文献[7]提出多输入多输出(Multi-Input Multi-Output, MIMO)OFDM通信系统,通过空间分集,提高水下通信系统的吞吐量。但由于MIMO信道间的相互干扰,导致水下通信系统所需的信道估计计算量较大不利于高速水声信道传输。文献[8]提出一种空时分组编码(Space Time Block Coding,STBC)传输的水下MIMO通信方法,该方法利用数据块的空时正交特性可以有效降低误码率,但该方法要求连续2个数据块传输时段内,水下信道保持稳定,由于水下环境的不稳定性,信道时变性较强,不同数据块传输所经历的信道时间相干性难以保证,实现难度较大。文献[9]提出一种基于空频分组编码(Space Frequency Block Coding,SFBC)传输的MIMO-OFDM水下通信方法。该方法通过空间调制编码,获得分集增益,提高信道传输的可靠性,但对于严重时延扩展的水声信道,由于频率深衰落而造成频率相关性较弱,从而导致该系统的通信性能下降。文献[10]提出一种多阵元接收Turbo均衡,该算法尽管采用时反、多阵元合并等简化算法,但由于状态数随信道长度指数增长,因而计算复杂度仍较高。
针对上述问题,本文研究了空频编码MIMOOFDM传输中的空频相关性,提出空频迭代信道估计与均衡(SFICEE)方法。该方法结合双发射阵元的Alamouti空频分组编码,在各个阵元处进行空频正交信道估计,并采用空频均衡获得符号的初始估计。其次,利用符号估计值迭代反馈,更新信道估计,并通过空频软均衡,进一步降低MIMO-OFDM水下通信的误码率。
文中(·)T、(·)∗、(·)H分别表示转置、共轭和共轭转置运算,tr(·)表示矩阵求迹运算,‖·‖为范数运算,diag{·}是将向量作为对角线元素形成的方形矩阵,E(·)表示期望运算,Cov(·)表示协方差运算,即为Cov(x,y)=E(xyH)-E(x)E(yH), IM表示M×M维单位矩阵,OM×N表示M×N维全零矩阵。
1 系统模型
针对水下信道多径干扰较大,通信时延较长导致通信误码率较大的问题。本文研究了基于空频块编码的MIMO-OFDM水下通信系统,在该通信系统的发射端中,将空频编码后的OFDM调制信号利用2个发射阵元通过水下信道进行传输。在系统接收端通过元阵列接收,SFBC-MIMO-OFDM水下通信系统如图1所示。
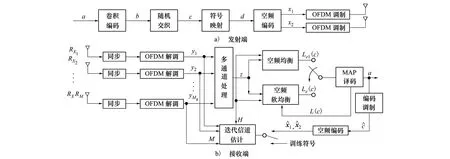
图1 SFBC-MIMO-OFDM系统框图
在发射端,第n个MIMO-OFDM数据块包含长度为Na的待传输信源比特序列a(n)=[a(n)(0),…, a(n)(Na-1)]T,其中a(n)(j)∈{0,1},j=0,…,Na-1。首先,对此序列进行码率为Rc=Na/N的卷积编码,可得b(n)=[b(n)(0),…,b(n)(N-1)]T;其次,为了避免突发误码,并降低相邻编码位的统计相关性,对编码序列b(n)进行随机交织,得到二进制交织序列c(n);再次,采用M阶PSK调制,将c(n)序列分组为长度为Q=log2M的符号调制子序列,即有c(n)=[c(n)T(0),…,c(n)T(K-1)]T,K=N/Q,其中各子序列为c(n)(k′)=[c(n)(k′,1),c(n)(k′,2),…,c(n)(k′, Q)]T,k′=0,1,…,K-1。此后,将每个二进制交织子序列c(n)(k′)通过M阶PSK调制映射为星座符号集S={α1,α2,…,αM}中的符号d(n)(k′),其中αm∈C,m=1,…,M对应的二进制序列图样为sm=[sm,1,sm,2,…,sm,Q]T,c表示复数集。
对d(n)=[d(n)(0),…,d(n)(K-1)]T进行空频分组编码,定义d(n)(k)=[d(n)(2k),d(n)(2k+1)]T为MIMO-OFDM数据块n中第k个载波对调制的数据符号,有k=0,…,k/2-1。本文采用类Alamouti空频分组编码,其对应发射阵元1、2在第k个载波对上的发射符号分别为
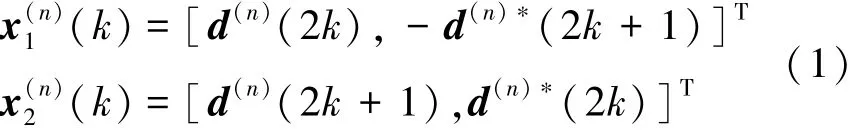

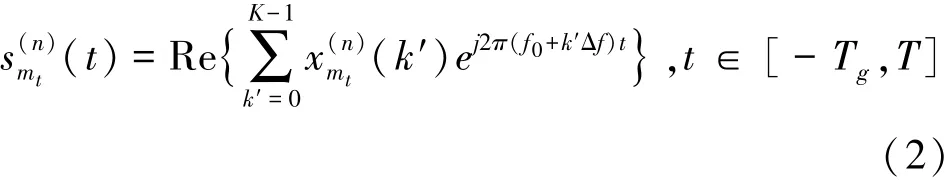
式中,T=1/Δf为OFDM符号时长,Tg为循环前缀时长。为了避免数据块间干扰,本文所采用的循环前缀的长度大于信道时延长度。设MIMO-OFDM调制信号从第mt个发射阵元通过水下信道传输到达第mr个接收阵元所经历的信道冲激响应函数为
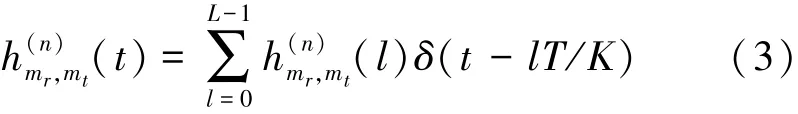
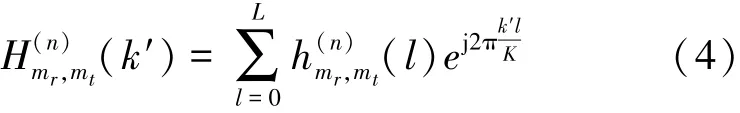
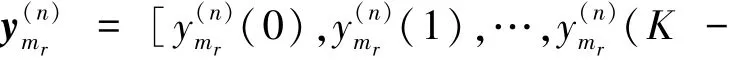
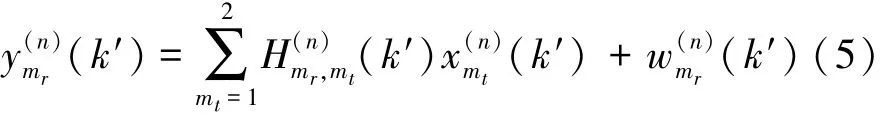
2 空频迭代信道估计与均衡
2.1空频正交信道估计
针对水下信道中具有快速时变特性,本文接收机信道估计不采用基于数据块间信道相关假设的自适应方法,而是采用逐数据块处理。假设信道等效基带时延最大长度为L,则对于每个发射阵元的OFDM信号而言,必须包含至少L个训练子载波。为此,本文等间隔设置L个训练载波对,各训练载波对间距统一为K/L个子载波,发射阵元传输互不重叠的训练载波,即训练载波空频域正交。发射阵元mt=1,2,所传输的训练序列所对应的载波频率为kt,其中k1=mK/L,k2=mK/L+1,m=0,…,L-1。根据公式(5),可得第mr个接收阵元(mr=1,2,…, MR)在载波kt上接收到的序列可表示为
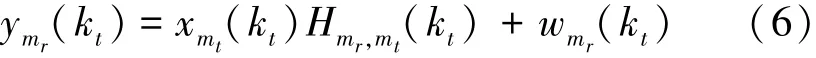
假设PSK调制采用单位幅度星座,即‖xmt(kt)‖2=1。由此可得,空频分组编码OFDM系统第mt个发射阵元与第mr个接收阵元间载波kt的信道频率响应最小二乘估计为


在符号估计迭代反馈过程中,判决得到的估计序列经过编码交织和符号映射,代替(6)式中的训练序列进行面向判决的迭代信道估计。此时,根据空频块编码的“Alamouti假设”,假定信道相关带宽大于OFDM子载波间隔即,则信道频率相关性满足OFDM相邻子载波间频率响应变化特性,因而第k个载波对所对应载波索引2k、2k+1上的信道响应近似相等,即
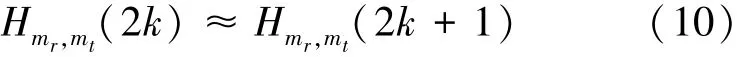
由此,空频分组编码MIMO-OFDM系统对应于子载波2k的信道频率响应最小二乘估计可得
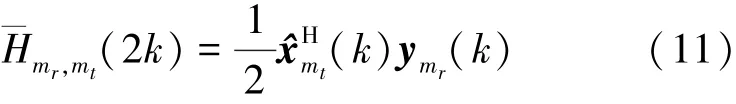
式中,mt=1,2,k=0,…,K/2-1且mr=1,…,Mr。将所得信道频域估计代入(8)式、(9)式,其中载波索引kt更新为2k,则可得到迭代更新的信道冲激响应估计。
2.2空频均衡
在空频正交信道估计的基础上,本文采用空频均衡获得初始化符号估计,具体方法如下:

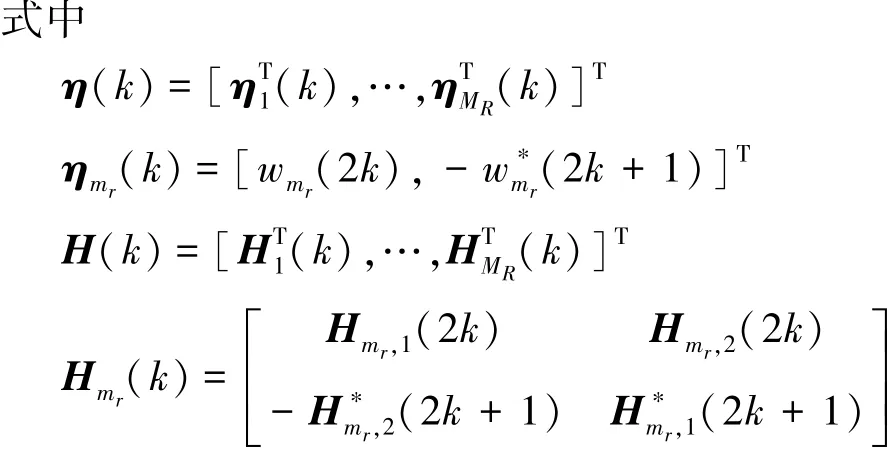
根据公式(10)建立空频块编码“Alamouti假设”,可将第k个载波对所对应的Z向量z(k)近似为
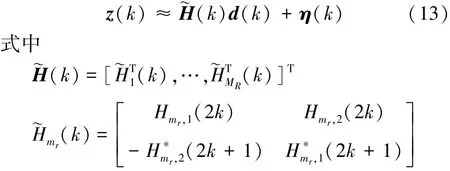
则通过空频均衡可得,2个发射阵元在第k个

2.3空频软均衡
在空频均衡获得初始化符号估计的基础上,本文所提MIMO-OFDM接收机方法采用空频迭代软均衡算法来消除多径干扰等水下信道干扰以降低通信系统的误码率。主要原因包括以下2个方面:①前述空频译码基于空频块编码“Alamouti假设”,其成立条件为Δf≪Bcoh也即L≪BT,这对于具有严重时延扩展的水下信道而言很难被满足,而仅采用公式(13)进行空时译码符号估计将产生较大的载波符号间干扰;②由于水下信道的频率选择特性,部分数据块可能经历深衰落影响,从而导致符号检测误码的增加。在此情况下,本文提出的空频软均衡流程如图2所示。

图2 空频软均衡流程图
首先,对于第k个载波对的Z向量z(k),根据符号映射关系可得交织序列信息位c(k′,i)的外部对数似然比可表示为

发射端采用随机交织,可认为c中的各元素相互独立,因而
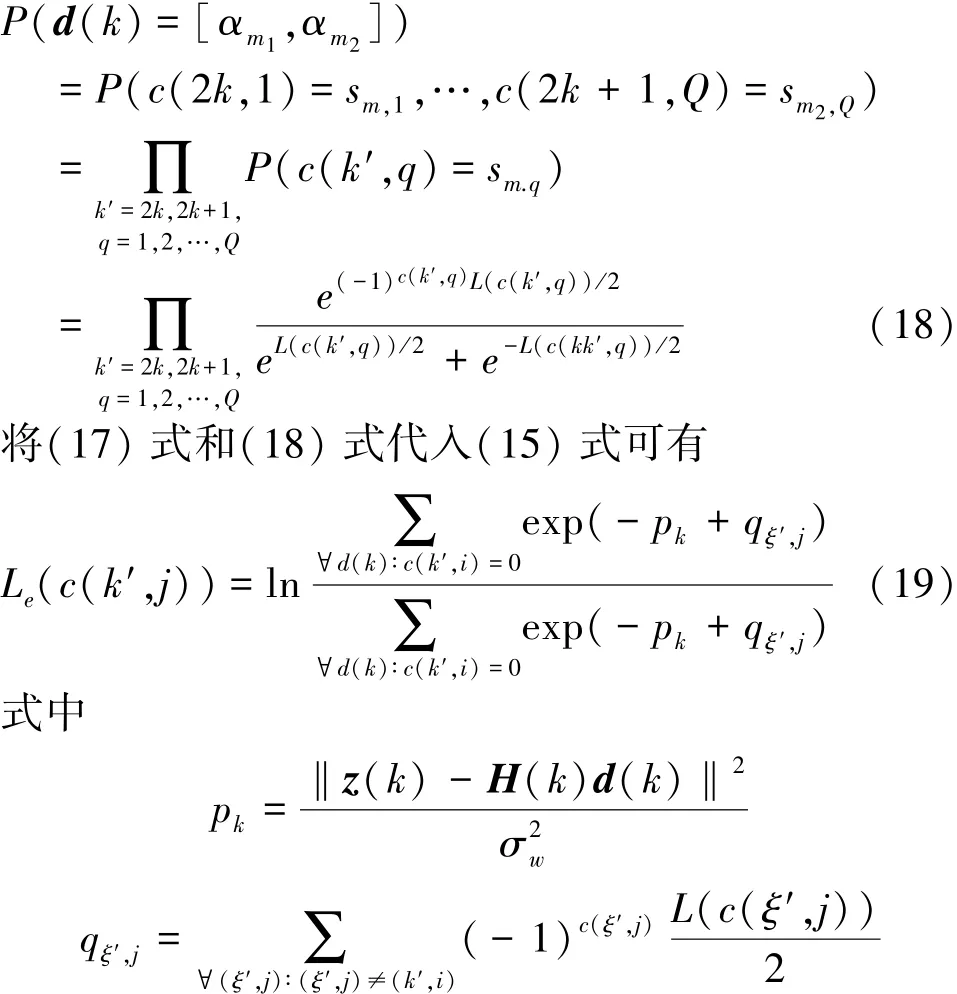
对于任一载波对k传输符号d(k)有M2种可能的符号取值,因此上式外部对数似然比Le(c(k′,i))包含M2个项解算。最后,对(19)式所得的Le(c(k′,i))进行解交织以及MAP译码,再通过译码器输出软信息反馈,即可实现空频迭代软均衡。
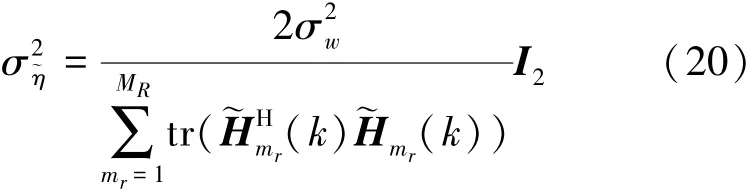
由此可得到MAP信道译码模块所需的交织序列外信息,即c(k′,i)的对数似然比为

将上式结果进行MAP译码即可得到空频软均衡所需的交织序列初始化先验信息。
3 仿真分析
在仿真中,本文假设检验信道最大延时为15 ms,发射阵元间距5 m,布放在水下20 m,接收端采用4阵元接收,阵元孔径4 m,收发距离450 m。发射端采用2个发射阵元传输Alamouti空频编码的OFDM信号,OFDM信号带宽4 kHz,即信道时延扩展约60个码元宽度。设定接收端已经完成初始相位和载波同步,即本文中不讨论信道间的同步问题。
3.1误码率比较
将本文方法的一次迭代和二次迭代结果与文献[6]所采用的SISO-OFDM传输,文献[8]所采用的基于STBC传输的水下MIMO通信方法和文献[10]所提出的基于SFBC传输的MIMO-OFDM水下通信方法进行误码率比较,所得结果如图3所示。

图3 误码率性能对比
图3中,信噪比表示水听器阵元处接收信号能量与噪声能量的比值。由图3中可以看出,文献[6]所采用的SISO方法在相同的导频数目下,无法完美的估计和消除水下信道中的多径干扰,所以当信噪比大于14 dB时,误码率下降缓慢。文献[8]所提出基于STBC传输的方法尽管利用了发射信号的空时正交性,但由于忽略了数据块间信道的变化,在误码率为10-3时,所需信噪比为8.3 dB。而文献[10]所提出的基于SFBC传输的方法,满足只有一个数据块内的信道不变,因而误码性能相对提升,在误码率为10-3时,信噪比为6.3 dB。而本文所提出的基于迭代信道估计的SFICEE均衡算法,由于提高了信道估计的准确性,并进行了软信息反馈迭代均衡,在误码率为10-3时,所需信噪比为3.5 dB。由于采用频域均衡,反馈均衡过程中进行逐载波对的迭代,在对载波对中某一载波处的符号进行估计时,只利用了载波对中另一载波处的先验信息,因而在高信噪比条件下,性能提升较慢,其优点在于状态数较少,迭代均衡产生的计算量较低。
3.2星座图比较
为了更加准确地比较算法性能,本文在输入信噪比为5 dB条件下,对算法的接收符号星座图进行了比较,结果如图4所示。
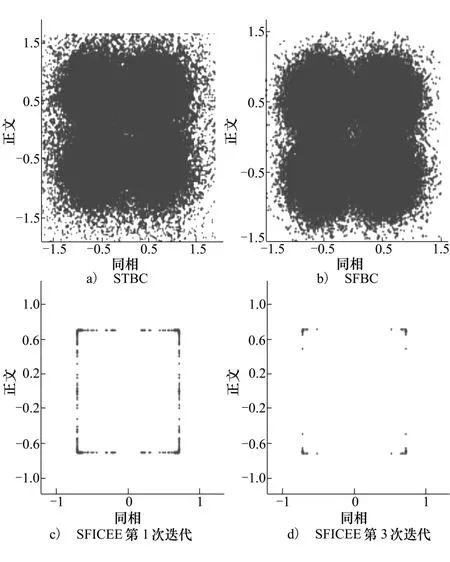
图4 各方法符号星座图比较(RSN=5 dB)
由图4中可以看出,文献[10]所提出的基于SFBC传输的MIMO-OFDM水下通信方法的星座图收敛性优于文献[8]所采用的STBC通信方法。而本文所提出的基于迭代信道估计的SFICEE均衡算法,由于提高了信道估计的准确性,并进行了软信息反馈迭代均衡,星座图逐步收敛于QPSK符号映射星座,可以有效完成水下通信系统的信号传输。
4 结 论
针对水下通信环境中多径干扰大,信号衰减快的特点,本文提出了一种基于空频编码MIMOOFDM通信的空频迭代信道估计与均衡(SFICEE)方法。该方法首先采用空频正交信道估计和空频均衡,为后续的迭代信道估计和均衡处理提供交织符号序列起始先验软信息。然后采用空频软均衡,通过软信息迭代反馈,进一步提高符号检测概率。文中从误码率、星座图这2个方面对本文所提出的方法和现有的水下通信方法进行了仿真比较。从仿真结果中可以看出,本文所提出的空频迭代信道估计与均衡方法能有效降低水下通信系统的误码率,当误码率容限为10-3时,经过二次迭代与STBC方法相比具有4.8 dB的性能增益,相对于SFBC方法有2.8 dB的性能提升,由此说明该方法可实现低信噪比下的水下通信系统高可靠传输。
[1] Stojanovic M.Efficient Processing of Acoustic Signals for High-Rate Information Transmission over Sparse Underwater Channels[J].Elsevier Journal on Physical Communication,2008,1(2):146-161
[2] Stojanovic M,Preisig J.Underwater Acoustic Communication Channels:Propagation Models and Statistical Characterization[J]. IEEE Communications Magazine,2009,47(1):84-89
[3] Qu F,Nie X,Xu W.A Two-Stage Approach for the Estimation of Doubly Spread Acoustic Channels[J].IEEE Journal of Oceanic Engineering,2015,40(1):131-143
[4] 尹艳玲,乔钢,刘凇佐,等.基于基追踪去噪的水声正交频分复用稀疏信道估计[J].物理学报,2015,64(6):227-234
Yin Yanling,Qiao Gang,Liu Songzuo,et al.Sparse Channel Estimation of Underwater Acoustic Orthogonal Frequency Division Multiplexing Based on Basis Pursuit Denoising[J].Acta Physica Sinica,2015,64(6):227-234(in Chinese)
[5] 张玲玲,黄建国,韩晶,等.基于短时傅里叶变换的水声通信自适应OFDM均衡[J].系统工程与电子技术,2015,37 (4):918-921
Zhang Lingling,Huang Jianguo,Han Jing,et al.Adaptive OFDM Equalization in Underwater Acoustic Communication Based on Short Time Fourier Transform[J].Systems Engineering and Electronics,2015,37(4):918-921(in Chinese)
[6] Li B,Zhou S,Stojanovic M,et al.Multicarrier Communication over Underwater Acoustic Channels with Nonuniform Doppler Shifts[J].IEEE Journal of Oceanic Engineering,2008,33(2):198-209
[7] Pelekanakis K,Baggeroer A B.Exploiting Space-Time-Frequency Diversity with MIMO-OFDM for Underwater Acoustic Communications[J].IEEE Journal of Oceanic Engineering,2011,36(4):502-513
[8] Eghbali H,Stojanovic M,Muhaidat S.Differential Decoding for SFBC OFDM Systems in Underwater MIMO Channels[C]//2014 IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP),Florence,Italy,2014
[9] 许浩,朱敏,武岩波.一种水声通信中的多阵元Turbo均衡算法[J].电子与信息学报,2014,36(6):1465-1471
Xu Hao,Zhu Min,Wu Yanbo.An Algorithm of Multi-Array Turbo Equalization of Underwater Acoustic Communication[J]. Journal of Electronics&Information Technology,2014,36(6):1465-1471(in Chinese)
[10] Zorita E V,Stojanovic M.Space-Frequency Coded OFDM for Underwater Acoustic Communications[J].IEEE Journal of Oceanic Engineering,2014,40(2):303-314
SFICEE(SPatial-Frequency Iterative Channel Estimation and
Equalization)in Underwater Acoustic MIMO-OFDM Communication
Zhang Lingling,Huang Jianguo,Han Jing,Zhang Qunfei
(College of Marine Science and Technology,Northwestern Polytechnical University,Xi′an 710072 China)
In MIMO-OFDM underwater acoustic communication system,mutual channel interference and frequency domain deep selectivity due to serious time delay in underwater acoustic channel lead to severe communication performance.We present SFICEE method for space frequency block coding MIMO-OFDM communication system.In this receiver algorithm,channel of each transceiver pair is estimated through taking advantage of the space frequency orthogonal characteristics.Then spatial frequency equalization is introduced to obtain initial symbol estimation. The symbol estimation is iteratively fedback to update the channel estimation and forwarded to spatial frequency soft equalization.Simulation and analysis show that,the proposed method gains about 4.8 dB as compared with STBC system and 2.8dB as compared with SFBC system after two iterations.And also this method gets great output signal to noise ratio(RSN)improvement,as can be seen from the convergence of constellation,and shows visible reduction in bit error ratio.
algorithm,bit error rate,computer simulation,covariance matrix,convergence of numerical methods, estimation,flowcharting,iterative methods,least squares approximations,MIMO systems,orthogonal frequency division multiplexing,probability density function,random variables,signal to noise ratio, stochastic systems,time delay,underwater acoustics,vectors;MIMO channel,STBC(space time block coding);SFICEE(spatial-frequency iterative channel estimation and equalization),underwater acoustic communication
TN929.3
A
1000-2758(2016)02-0208-07
2015-10-13基金项目:国家自然科学基金(61271415、61471298、61531015)、水下信息处理与控制国家重点实验室基金(9140C231002130C23085)、西北工业大学博士论文创新基金(CX201230)及西北工业大学基础研究基金-中央高校基本科研业务费专项基金(3102014JCQ01010)资助
张玲玲(1986—),女,西北工业大学博士研究生,主要从事水声通信、信道均衡研究。
