基于反步法的小型无人直升机位置控制器设计*

曹永军陈再励

（1.广东省智能制造研究所 广东省现代控制与光机电技术公共实验室 2.华南智能机器人创新研究院）

基于反步法的小型无人直升机位置控制器设计*

曹永军1,2陈再励2

（1.广东省智能制造研究所 广东省现代控制与光机电技术公共实验室 2.华南智能机器人创新研究院）

针对小型无人直升机的位置控制问题，提出一种基于反步法的控制器设计方法。基于小型无人直升机非线性模型的刚体动力学，采用反步法得到力和力矩控制量，再通过数值分析得到最终舵机的控制量。通过李雅普诺夫稳定性定理严格分析了系统的稳定性，最后通过仿真，验证了控制器具有良好的位置控制性能。

无人直升机；反步法；位置控制

0 引言

小型无人直升机具有垂直起降、定点悬停的飞行特性，受场地限制影响小，且能够低空、低速在城市楼宇、山川、森林等复杂地形环境中飞行，在军事和民用领域都具有较高的应用价值。目前，小型无人直升机自主飞行控制的问题得到了国内外研究者的重点关注。

部分研究者采用强化学习等智能控制[1]方法设计飞行控制器，取得一定成果，但这类方法需要采集大量的飞行数据，同时依赖地面操控人员的经验。还有部分研究者基于直升机的线性模型，采用LQG、PID等方法设计小型无人直升机的姿态、位置控制器[2]。但小型无人直升机的系统模型是典型的含高阶非线性的系统模型，采用基于线性模型的设计方法，通常需要将其系统模型在平衡点附近进行近似线性化处理，导致控制器性能在飞行状态偏离平衡点时受到影响。基于上述情况，越来越多的研究者采用非线性方法，基于无人机的非线性模型设计控制器，比如滑模控制[3]、非线性模型预测控制[4]等。

高精度的位置控制是小型无人直升机自主飞行、轨迹跟踪的基础，本文主要介绍基于小型无人直升机非线性模型的位置控制器设计。非线性控制方法对控制对象的模型精度有很高的要求，因此本文综合考虑了小型无人直升机的系统模型。通过对小型无人直升机非线性模型的研究，其状态方程的上三角特点十分适合采用反步法进行控制器设计[5]，同时采用反步法设计的控制器具有较快的响应速率。

1 无人直升机系统模型

小型无人直升机是典型的欠驱动系统，其非线性模型如图1所示，包括刚体动力学模型、力和力矩表达式、主旋翼/尾旋翼挥舞动力学方程、舵机伺服动力学模型等4部分。

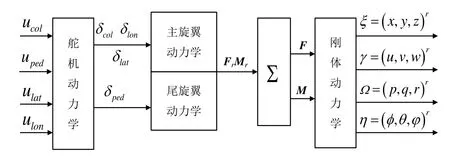
图1 无人直升机系统模型

小型无人直升机可以视为一个六自由度的刚体，在惯性坐标系下满足

其中，ξI=（x, y, z）T是惯性系下的位置向量；VI是惯性系下的线速度向量；g是惯性系下的重力加速度；R表示由体坐标系到惯性坐标系的转移矩阵，其表达式为

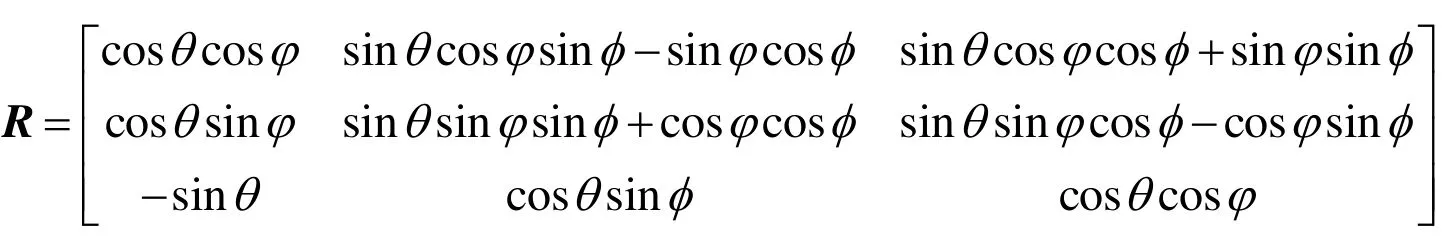
其中，φ为横滚角；θ为俯仰角；φ为偏航角。

考虑在体坐标系下的机体线速度和角速度，得到表达式

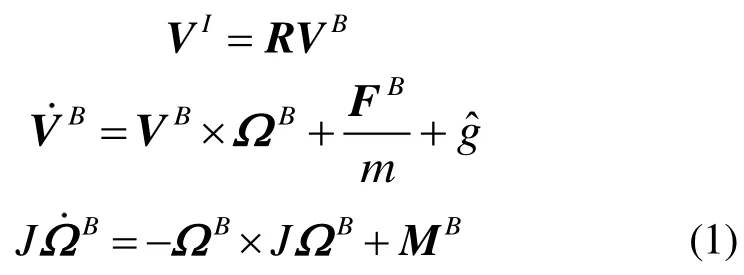
其中，VB=(u, v, w)T是体坐标系下的线速度向量；ΩB=(p, q, r)T是体坐标系下的角速度向量；J、m分别是小型无人直升机的转动惯量和质量；FB=［Fx, Fy, Fz］、MB=［Lm,Rm,Nm］是作用在机体质心上的合外力和合外力矩；gˆ是体坐标系下的重力加速度，其表达式为

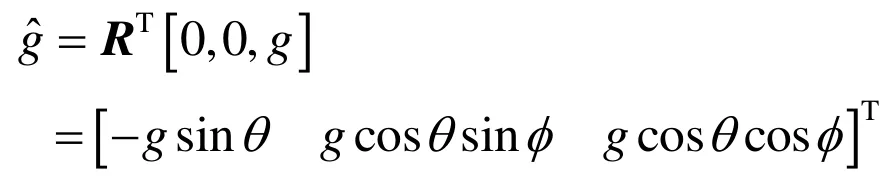
作用在直升机上的外力F和外力矩M表达式为

其中，Tmr、Tt分别表示主旋翼和尾旋翼产生的力；a1、b1是主旋翼的挥舞角度；dL/db1、dL/da1分别是横滚转矩系数和俯仰转矩系数；kx、kz是主旋翼在x轴和z轴方向上相对于直升机重心的距离；lx、lz是尾旋翼在x轴和z轴方向上相对于直升机重心的距离；MQ是主旋翼产生的扭矩。

主旋翼的挥舞角度可用挥舞动力学模型来描述，表征的是主旋翼桨面挥舞角度与周期距之间关系，考虑本文研究的无人直升机是带平衡杆的系统，平衡杆的挥舞动力学模型也要考虑：

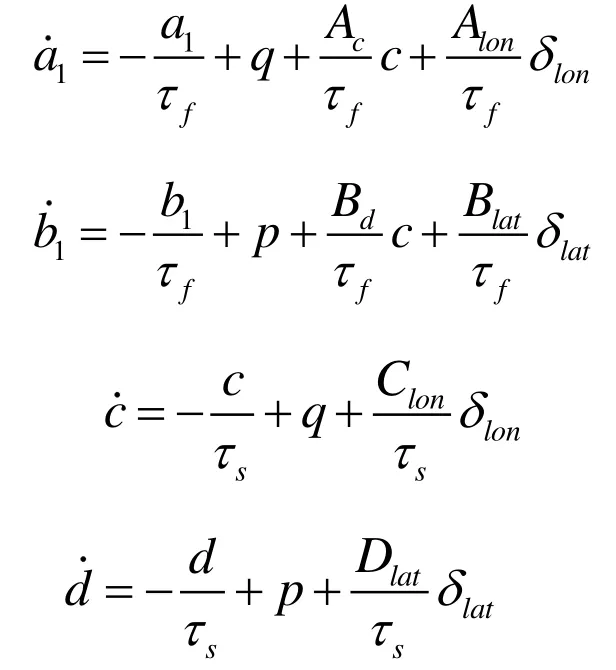
其中，δlon、δlat分别表示直升机的横向周期距、纵向周期距；c、d是平衡杆的挥舞角度；τf、τs是主、尾旋翼桨叶的挥舞时间常数；Ac、Alon、Bd、Blat、Clon、Dlat是与直升机结构相关的参数。

主旋翼产生的力Tmr与主旋翼总距δcol存在的近似关系式为

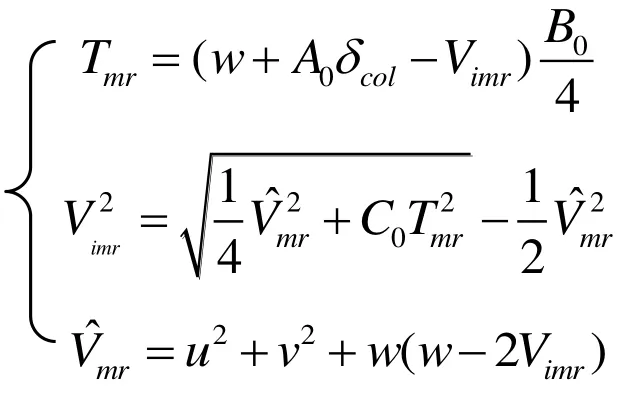
类似可以得到尾旋翼产生的力Tt和尾旋翼总距δped之间的表达关系式

小型无人直升机周期距、总距与舵机控制量之间的关系就是舵机的伺服动力学模型，可以用一阶微分方程来描述

其中ulon 、ulat 、ucol 、uped 是相应舵机的控制量；τlon、τlat是对应时间常数；Kcol、Kped是对应的比例常数。

2 控制器设计

控制器系统框图如图2所示。先基于小型无人直升机的动力学方程推导位置控制律，再代入挥舞动力学及舵机伺服动力学方程求得最终的控制量表达式。

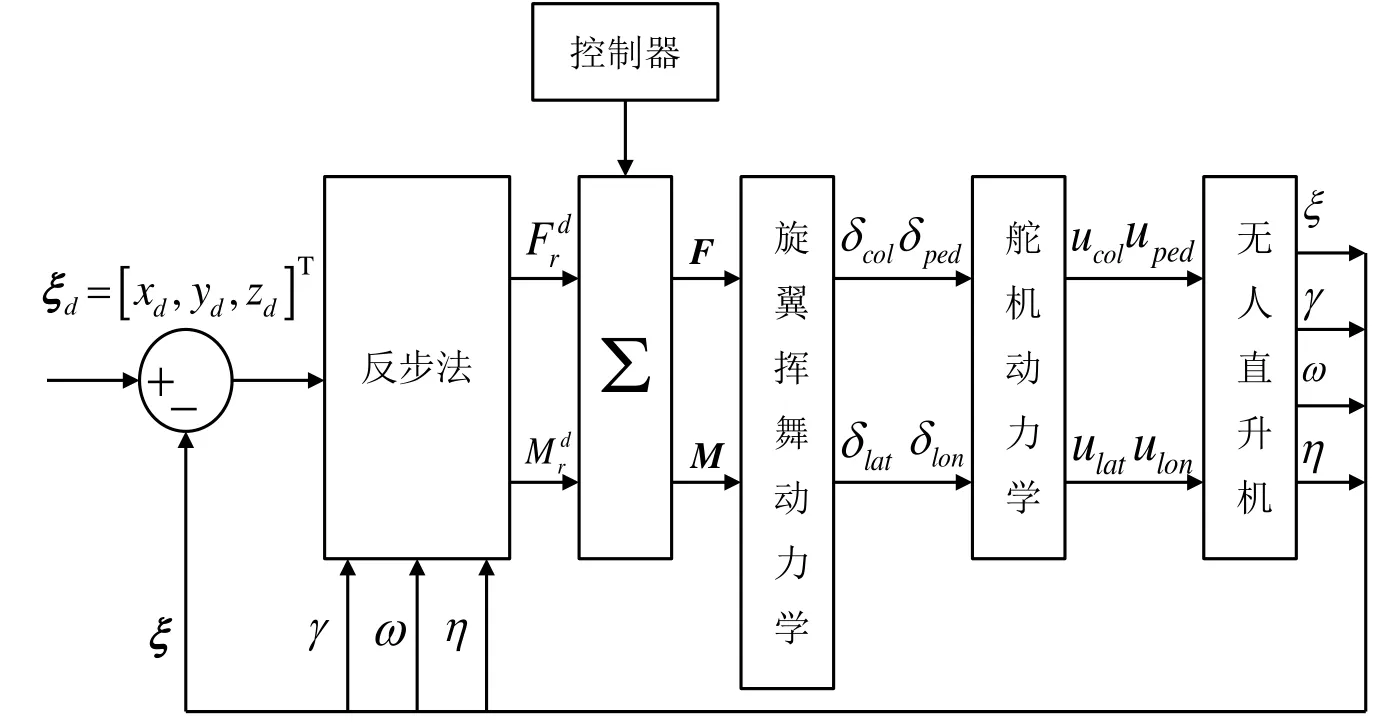
图2 控制器系统框图

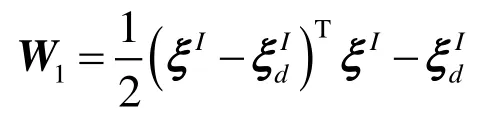
满足正定要求，对其求导可得

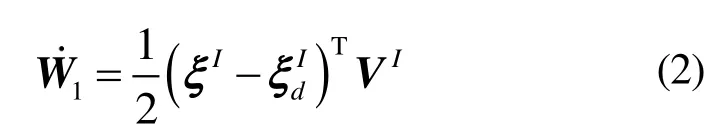
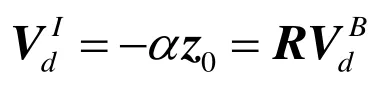
其中α是控制器参数，并且要求α>0。

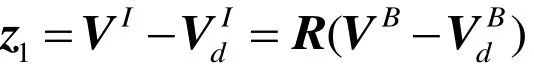
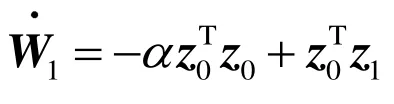
根据反步法步骤，考虑直升机的速度稳定到期望值，引入第二个李雅普诺夫候选函数

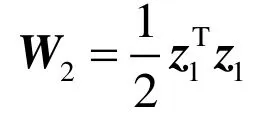
满足正定条件，对其求导

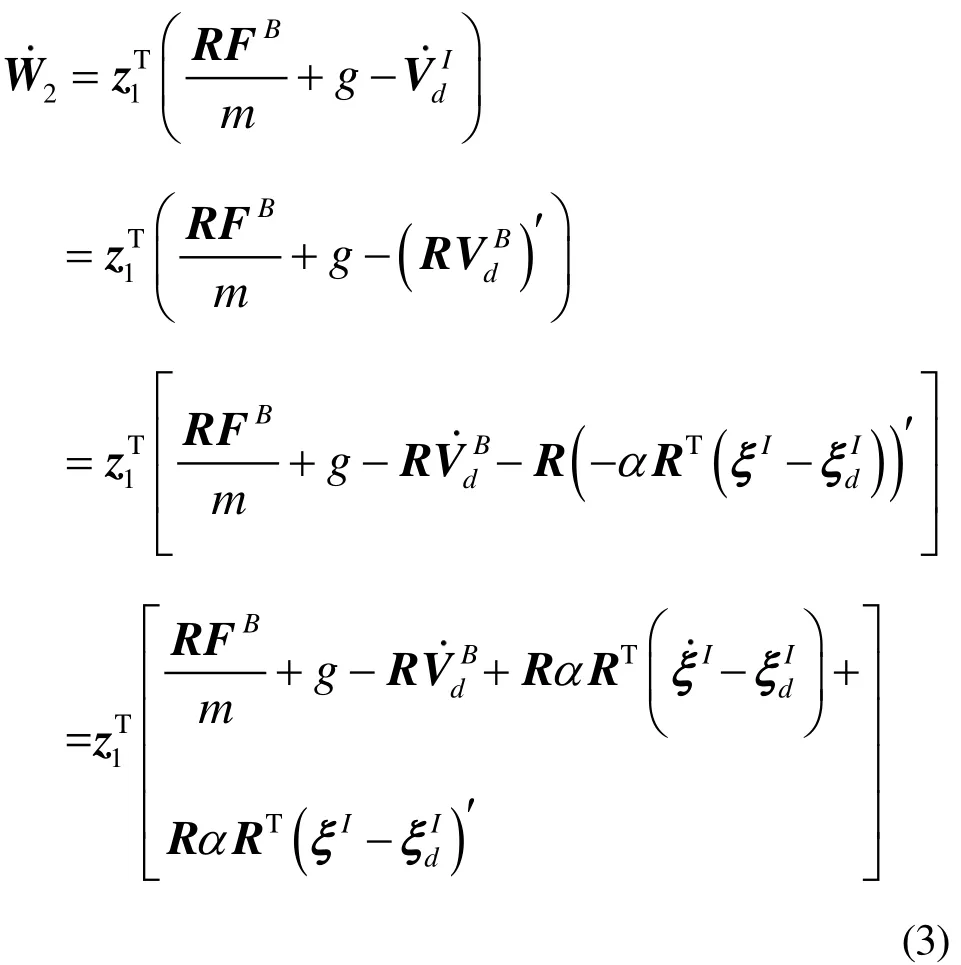
将式(4)代入式(3)中，整理化简第二个李雅普诺夫候选函数导数的表达式

再一次应用向量积性质

最终得到第二个李雅普诺夫函数导数

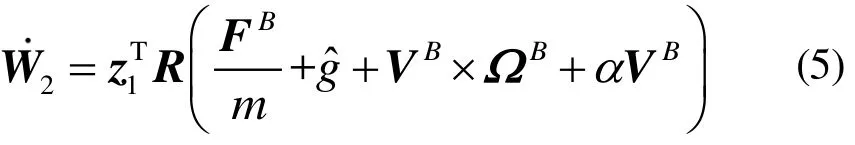
根据向量积性质，引入第二个控制参数β，并构造方程

设计控制律Fd满足

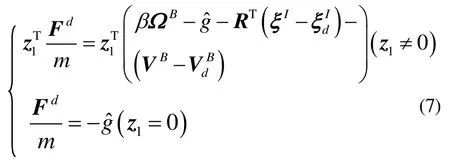
将式(5)和(6)代入到式(7)中，可以验证

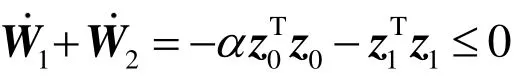
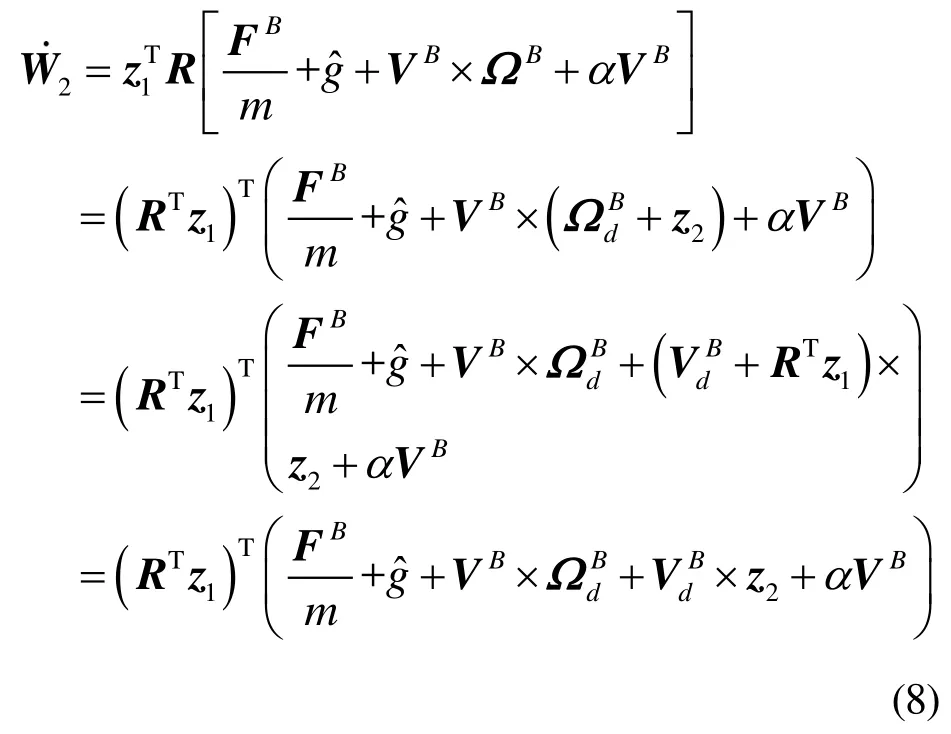
将式(6)和(7)代入到式(8)中，得到

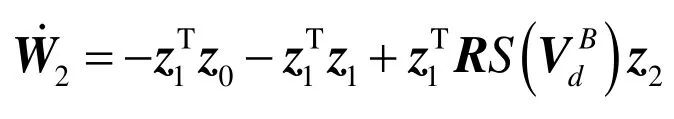
根据反步法步骤，设定第三个李雅普诺夫候选函数

满足正定条件，求导

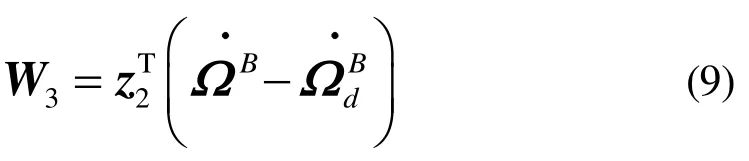
将式(1)代入到式(9)中，得到

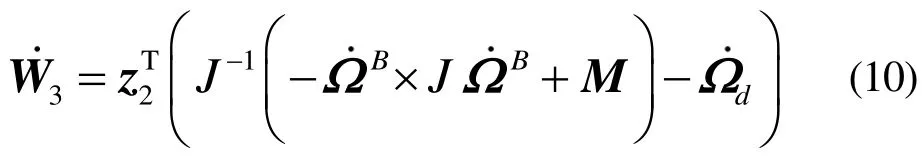
设计控制律dM满足

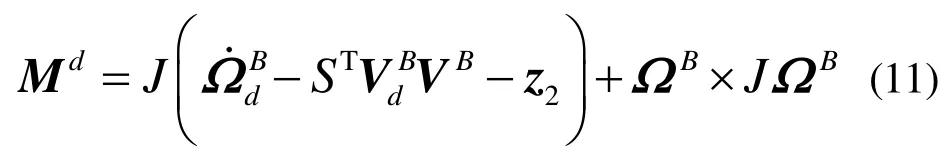
将式(11)代入式(10)中，得到

根据式(11)，可得到期望的角速度的值

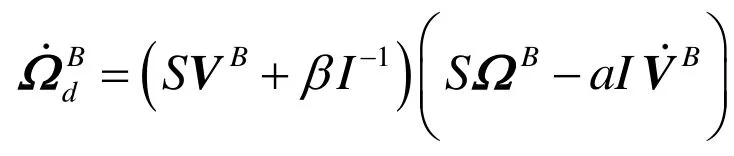
至此，已经根据反步法完成了控制律设计。下面利用李雅普诺夫稳定性第二方法进行系统稳定性的分析验证。

系统的李雅普诺夫候选函数为

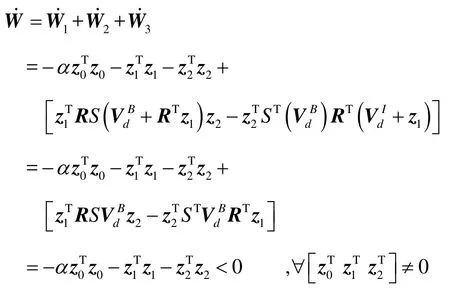
根据李雅普诺夫稳定性定理，系统渐进稳定。在有限时间内，小型无人直升机的位置、速度、角速度都会收敛到期望的状态，最终实现稳定的位置控制。

基于反步法完成了控制律（FBMB）的设计后，根据小型无人直升机力和力矩表达式、主旋翼平衡杆挥舞动力学模型，采用高斯牛顿的方法计算出Tmr、Tt、a1、b1代入到舵机伺服动力学方程，最终得到输出给无人直升机执行机构舵机的控制量ucol、uped、ulat、ulon，实现对小型无人直升机系统的位置控制。

3 仿真与分析

根据本文提出的位置控制器设计方法，利用Matlab/Simulink仿真软件搭建仿真实验平台，对位置控制的性能进行仿真验证。在仿真中，小型无人直升机的初始位置设定在（-5 m，-4.8 m，5 m），期望位置被设定在原点，仿真时间设为10 s。仿真中使用的小型无人直升机为HILOBO EAGLE航模直升机，具体参数如表1所示。

表1 HILOBO EAGLE-2参数

选取不同的控制器参数，对比不同参数对位置控制器性能的影响，仿真结果如图3所示。从仿真结果可以看到，参数主要影响系统的收敛时间和收敛过程中的超调量。小型无人直升机快速收敛到平衡点位置，收敛时间低于5 s，满足快速响应的要求。

可以看到当控制器参数α较小时，系统收敛时间较慢及出现超调；当第二个控制参数β较大时，系统的稳态结果效果相对变差。综合考虑，控制参数选取α=2.5，β=3时，位置控制器的控制性能较好，并给出此参数下速度、角速度和舵机控制量的仿真输出结果，如图4所示。可以看到速度、角速度和舵机控制量都会进行相应的正确反应，并且快速回归到无人直升机悬停时的平衡点状态。其中，主旋翼总距稳定在7deg左右，为主旋翼产生升力克服直升机重力的值。

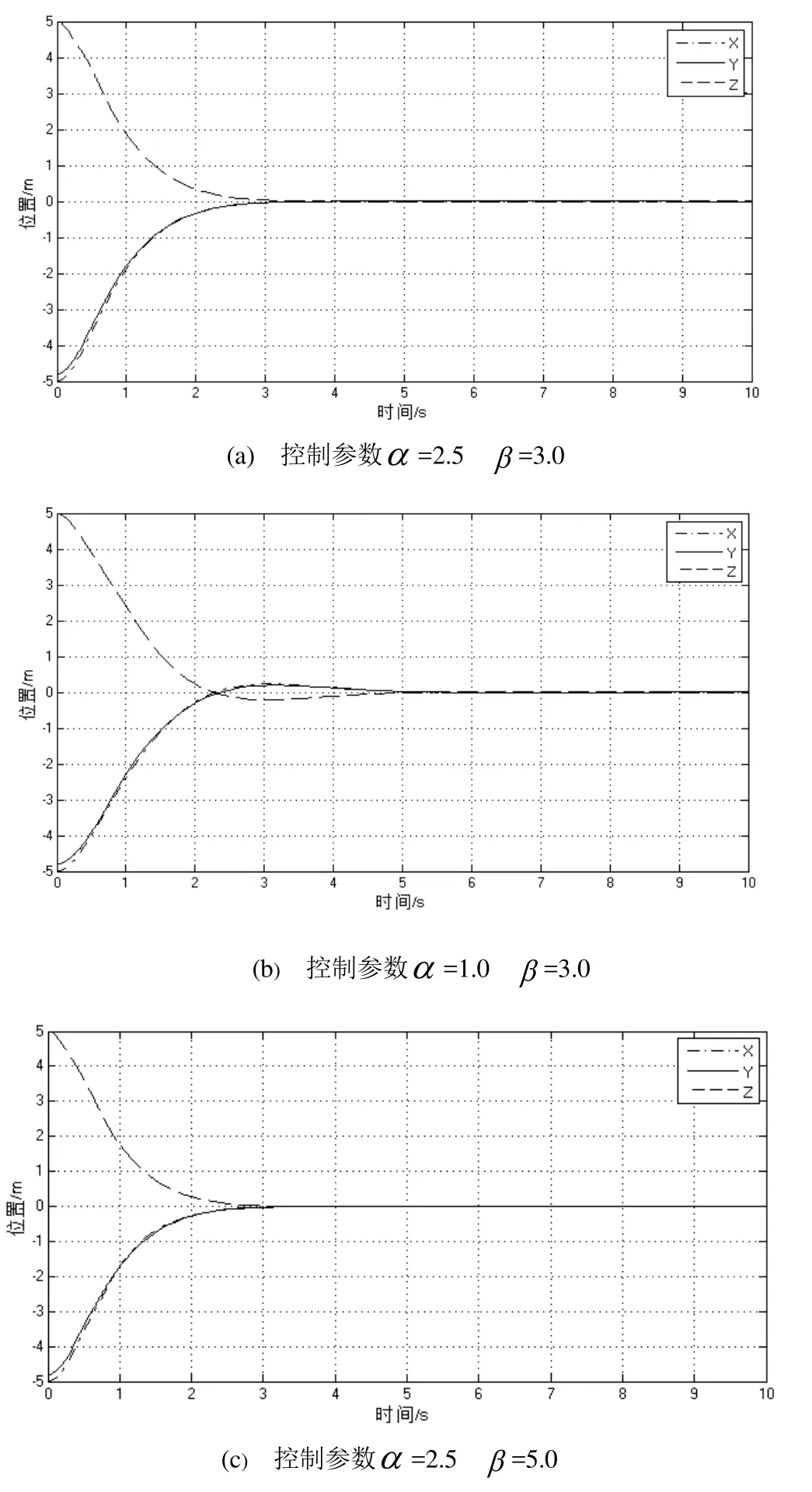
图3 不同参数下位置控制器性能

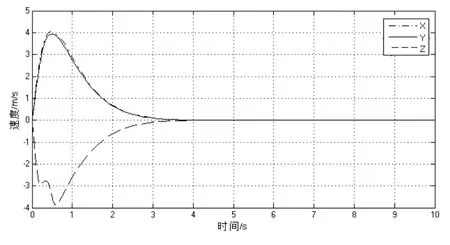
图4 (a) 速度输出量

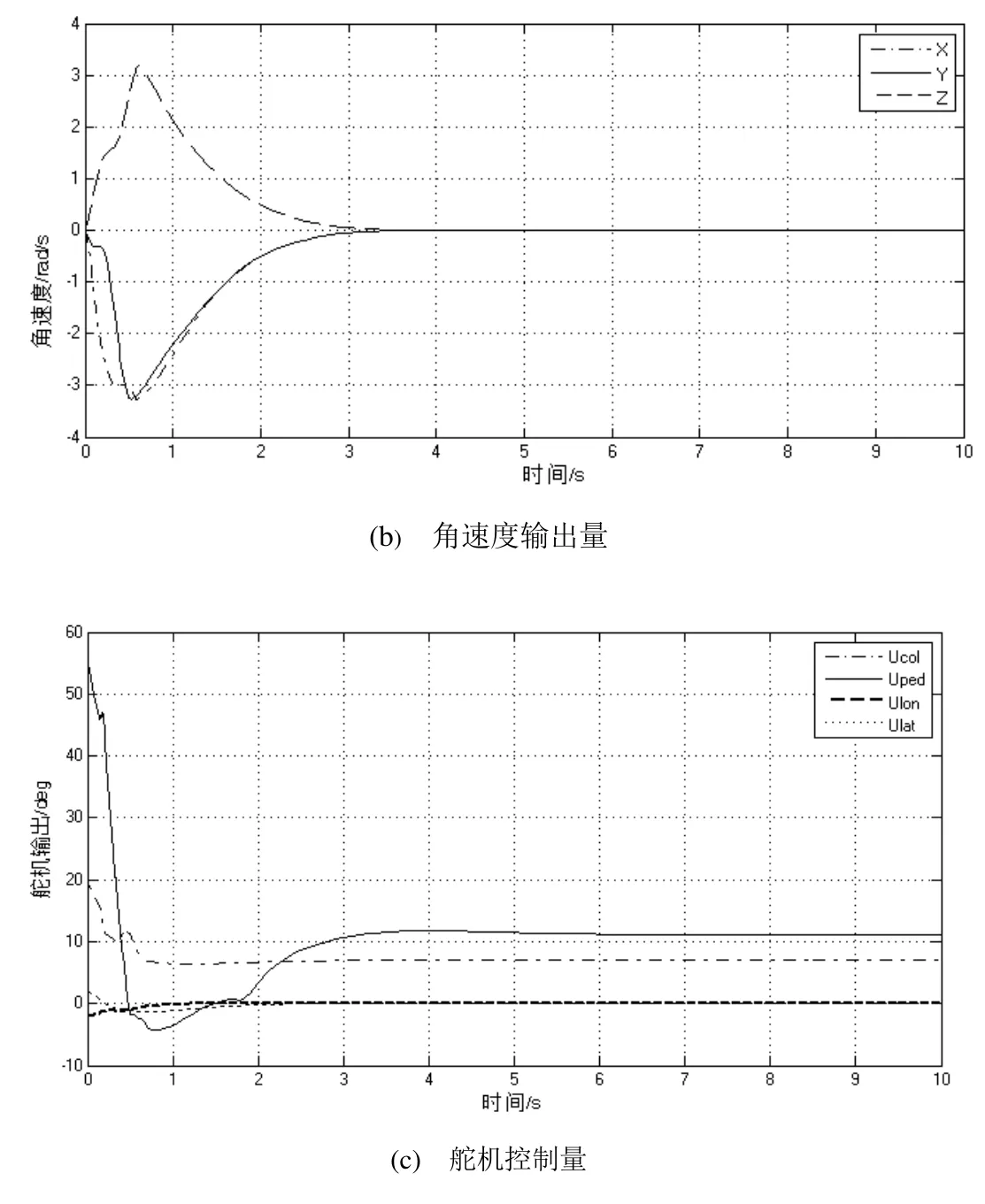
图4 控制参数α=2.5β=3.0下系统状态量输出

4 结论

本文提出一种基于反步法的小型无人直升机位置控制器设计方法。对无人直升机非线性模型采用反步法设计得到控制律，并通过理论分析和仿真实验验证了所设计的控制器具有渐进稳定性和较好的响应速率。本文提出的方法可以在李雅普诺夫重新设计的框架下进行进一步的扩展，实现轨迹跟踪和抗风干扰等控制应用。在接下来的工作中会进一步考虑无人直升机模型中的不确定性并引入外界环境风干扰的影响。通过对该算法进行扩展来实现在小型无人直升机系统中的实际应用。

[1] Abbeel P, Coates A, Ng A Y. Autonomous helicopter aerobatics through apprenticeship learning[J]. International Journal of Robotics Research, 2010,29(13):1608-1639.

[2] Bouabdallah S, Noth A, Siegwart R. PID vs LQ control techniques applied to an indoor micro quadrotor[J]. IEEE/RSJ International Conference on Intelligent Robots and Systems, 2004,3(3):2451-2456.

[3] Bouabdallah S, Siegwart R. Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[J]. in IEEE International Conference on Robotics and Automation, 2005(3):2247-2252.

[4] Molenaar P Z. Model predictive control to autonomous helicopter flight[M]. Technische Universiteit Eindhoven, Eindhoven, 2007.

[5] Mian A A, Daobo W. Modeling and backstepping-based nonlinear control strategy for a 6 DOF quadrotor helicopter[J]. Chinese Journal of Aeronautics, 2008,21(3):261-268.

The Position Control of Small Unmanned Aerial Vehicle Based on Backstepping

Cao Yongjun1,2Chen Zaili2
（1.Guangdong Institute of Intelligent Manufacturing Guangdong modern control and optical electrical and Mechanical Technology Public Laboratory 2.South China Robotics Innovation Research Institute）

This paper presents the design and verification of a backstepping based position controller on a small unmanned aerial vehicle (UAV). In this paper, the backstepping method is employed to design the force/moment, and the final servo controller can be derived by the numerical analysis method. The system proved to be asymptotical stable by Lyapunov method. Simulation results can illustrate the position control performance.

Unmanned Aerial Vehicle; Back Stepping; Position Control

曹永军，男，1981年生，硕士，高级工程师，主要研究方向：智能控制与系统、机器视觉等。E-mail:cyjauto@163.com

广东省科技计划项目(2015B010917001)；佛山市科技创新专项资金（2013HK100113）。

陈再励，男，1989年生，硕士，工程师，主要研究方向：无人机控制等。