抛物势量子点中强耦合双极化子量子比特的性质

额尔敦朝鲁,韩 超,张 颖

（河北科技师范学院物理系，河北秦皇岛 066004）

抛物势量子点中强耦合双极化子量子比特的性质

额尔敦朝鲁*,韩 超,张 颖

（河北科技师范学院物理系，河北秦皇岛 066004）

基于LLP幺正变换，采用Pekar型变分法得到了二维量子点中强耦合双极化子的基态和第一激发态的能量和波函数，进而构造了一个双极化子的量子比特。数值结果表明:在量子比特内，两电子的空间几率密度的时间振荡周期T0随电声子耦合强度α、量子点的受限强度ω0以及介质的介电常数比η的增加而减小;在量子比特内，两电子的空间几率密度Q随时间t、角坐标φ2及介电常数比η的变化而作周期性振荡;两电子在量子点中心附近区域出现的几率较大，而在远离量子点中心区域出现的几率很小。

量子点;双极化子;量子比特;Lee-Low-Pines-Pekar变分法

1　引 言

量子计算机（Quantum comPuter，QC）是目前信息科学的研究热点之一，它在很多方面都可以突破现有经典信息通信的极限，将给信息科学与通信技术带来深刻的革命，为计算机科学与技术的可持续发展开辟了崭新的空间。量子计算机是遵循量子力学规律进行高速数学和逻辑运算、存储及处理量子信息的物理装置，其基本信息单位是量子比特（Qubit）。量子比特是两个任意正交量子态的叠加态许多两态量子系统均可作为qubit的载体，如二能级原子、光子的两个偏振态、电子的两个自旋态等。近年来，人们提出了多种实现量子比特的方案，如离子阱[1]、核与电子自旋[2-3]、量子点[4]等。量子点具有能级结构可调、可以实现全光操作、便于实现量子比特的集成等优点，有可能作为量子光学技术的基本单元，因此，许多学者[5-8]对量子点量子比特进行了研究，获得了一系列重要结果。最近，人们对量子点中电子与声子相互作用对量子比特的影响进行了研究。Yu等[9]研究了单电子量子点量子比特的消相干，Xiao[10]研究了非对称量子点量子比特的电场效应，Chen等[11]讨论了电场中抛物量子点量子比特的温度依赖性，Sun等[12]研究了磁场对抛物量子点量子比特的消相干时间的影响。然而，不难看出，这些研究仅限于讨论由单极化子的基态和第一激发态构造的量子比特。据我们所知，关于量子点中双极化子量子比特的研究工作至今尚无报道。事实上，由于大多数人工低维结构是离子晶体或极性半导体材料制备的，而且因维度的降低，使得量子点结构中电子-声子相互作用变得更强（电声子耦合强度α＞6.0），致使两个相同的电子通过声子场相互作用，将形成双极化子的束缚态[13-15]。毫无疑问，对这类材料的量子点结构而言，抑制双极化子的产生既无可能也无必要。随着人工材料制备高新技术的发展，研究其中形成的双极化子量子比特要比单研究极化子量子比特更有实际意义和潜在的应用价值。本文基于Lee-Low-Pines（LLP）幺正变换，采用Pekar型变分法，首次研究了二维量子点中强耦合双极化子的基态和第一激发态构造的量子比特的性质。

2　理论模型与方法

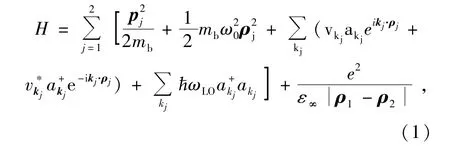
考虑被约束在一个二维（x-y平面）抛物势量子点中并与体纵光学（Longitudinal oPtical，LO）声子相互作用的两电子体系，体系的Frölich哈密顿量[15]为上式右边求和号中的4项依次表示单电子的动能、量子点的限定势、局域LO声子场的能量及电子-LO声子耦合项，最后一项表示两电子间库伦相互作用能。pj和ρj（j＝1，2）分别是两电子在x-y平面上的动量和坐标，ω0为电子所受量子点的约束势强度，和ɑkj分别是波矢为kj、频率为ωLO的LO声子的产生和湮灭算符，相互作用系数为

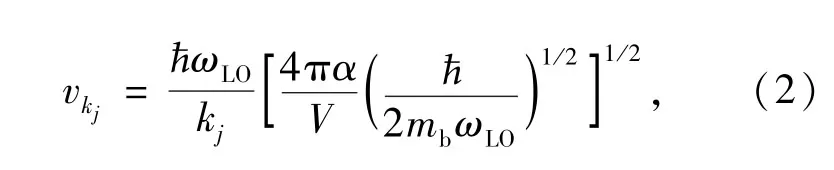
这里V是晶体的体积，α是无量纲的电子-声子耦合强度:

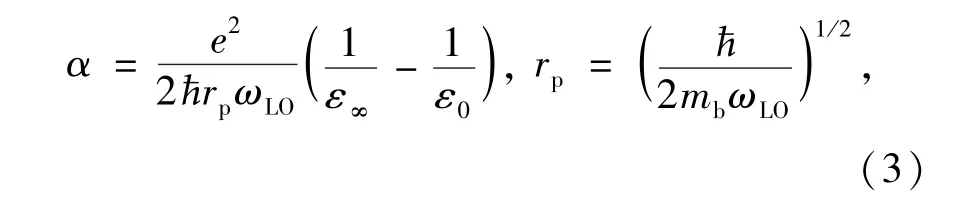
其中，ε∞（ε0）为电子所处介质的高频（静态）介电常数，rP为极化子的半径。

为了求体系的能量，我们讨论变分函数U-1HU 在态中的期待值的极值问题。按照变分原理

是LLP幺正变换[16]，其中，fkj和f*kj为变分参数。假设对于体系的基态和第一激发态，高斯函数近似成立，则依据Pekar类型的变分法[17]，体系的基态尝试波函数和第一激发态尝试波函数分别选为

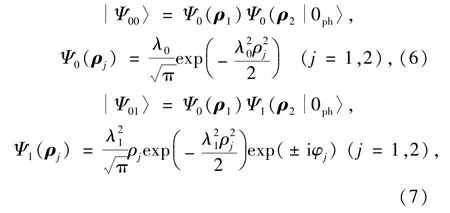
其中，λ0和λ1为变分参数，Ψ0（ρj）和Ψ1（ρj）分别表示单电子基态和第一激发态试探波函数，是声子的真空态。将式（1）～（3）和式（5）～（7）代入式（4）中，可确定变分参数fk、、λ1和λ2。再经过冗长的计算，得到双极化子体系的基态能量和第一激发态能量分别为

式中η＝ε∞/ε0称为介质的介电常数比。至此，可以构造一个二能级体系，当电子处于叠加态

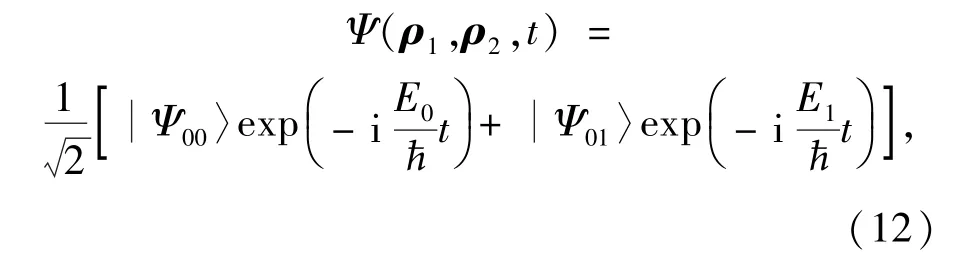
时，即构成一个量子点双极化子量子比特，量子比特内两电子的几率密度为

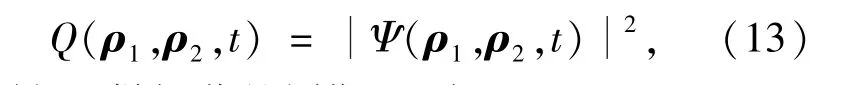
它随时间t做振荡的周期T0为

3　结果与讨论

为了直观地揭示准二维量子点中双极化子的基态能量E0、第一激发态能量E1、量子比特内电子的几率密度Q及其随时间变化的周期T0随量子点的受限强度ω0、介电常数比η、电子-声子耦合强度α的变化规律，我们给出了数值计算结果，如图1～7所示。图中各量采用极化子单位（2mb＝ħ＝ωLO＝1）。

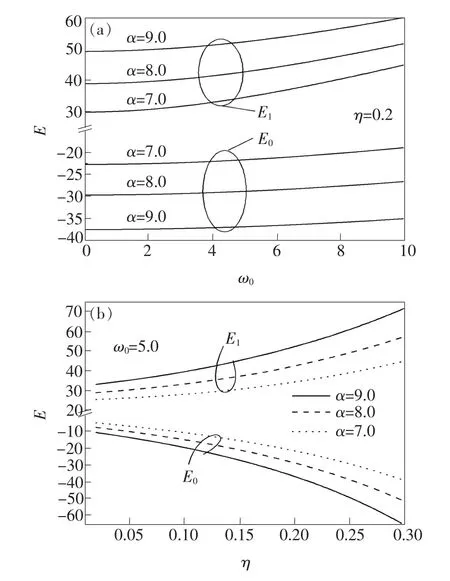
图1　双极化子的基态能量E0和第一激发态能量E1在不同电声耦合强度α下随受限强度ω0（a）及介电常数比η（b）的变化Fig.1　Variations of ground state energY E0and the first excited state energY E1of biPolaron with the confinement strength ω0（a）and the dielectric constant ratio η（b）at different electron-Phonon couPling strength α

图1描写了双极化子基态能量E0和第一激发态能量E1在不同电声子耦合强度α下随量子点的受限强度ω0（a）和介质的介电常数比η（b）的变化。由图1（a）、（b）可以看出，双极化子的基态能级E0＜0，而且基态能级掉得很低。这表明基态双极化子将处于较为稳定的束缚态，激发它需很大能量。因此，双极化子的第一激发态应该是由一个电子留在单粒子基态，而另一个电子被激发至单粒子第一激发态所形成。这就是本文选取式（6）为双极化子基态试探波函数及式（7）为第一激发态试探波函数的依据之一。由图1（a）可以看出，基态能量的绝对值随ω0的增加而减小，而第一激发态能量E1随ω0增加而增大;在ω0给定时，和E1都随α增加而增大。由图1（b）可以看出，和E1均随η的增加增大。物理原因分析如下:由于双极化子的能量当中的电声子相互作用能总是小于0[18]，所以由电子-声子耦合引起的两极化子间的相互作用是吸引力。在基态下，电声子相互作用能的绝对值大于激发态下电声子相互作用能的绝对值，这是因为体系处于基态时声子被激发的几率比激发态更大，致使基态双极化子周围声子平均数多于激发态双极化子周围声子平均数，导致基态双极化子的电声子相互作用要比激发态更强，以至于电声子相互作用能在基态能量中占主导地位，而在激发态中却不是。在激发态中，库仑势和量子点的约束势的能量变得更加重要，且它们的取值都是正定的，这可以说明图1中为什么双极化子的基态能量总是负的，而激发态能量不是，且两者随α、η和ω0的变化规律也不尽相同的物理原因。

图2表示了振荡周期T0在不同电声耦合强度α下随受限强度ω0（a）和介电常数比η（b）的变化。由图2（a）可以看出，T0随ω0的增加而减小。这是由E0、E1的正负号及其随ω0的变化规律不同导致的。由图1（a）可以看出，随着ω0的增加，E1随ω0的增大而增加，而基态能量是负的，其绝对值随受限强度ω0的增大而减小，且减小的幅度比E1随ω0的增大的幅度小，这使得能级差ΔE＝E1-E0随ω0的增加而增大，导致T0随ω0的增加而减小。当ω0给定时，T0随α的增加而减小。由图1（a）、（b）可以看出，随着α的增大，不仅随之增加，而且E1也随之增加。这是因为对双极化子的激发态而言，尽管电声子相互作用不再占主导，但它也通过影响库仑能（2α/（1-η））来抬高激发态的能量，使得能级差ΔE＝E1-E0随α的增加而增大，导致T0随α的增加而减小。由图1（b）可以看出，T0随η的增加而减小。这是因为随着η的增加，不仅E1增大，基态能量的绝对值也增大。当介电常数比η增大时，尽管两电子间库伦排斥力增加，但同时因两电子间空间电场强度的增大，势必引起两电子间介质的极化加强，以此进一步推高占据主导地位的电声子相互作用能，使得能级差ΔE＝E1-E0随η的增加而增大，导致T0随η的增加而减小。

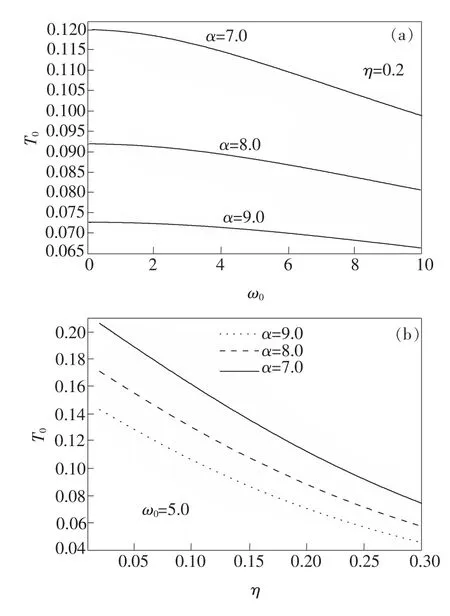
图2　振荡周期T0在不同电声耦合强度α下随受限强度ω0（a）及介电常数比η（b）的变化Fig.2　Variations of oscillation Period T0with the confinement strength ω0（a）and the dielectric constant ratio η（b）at different electron-Phonon couPling strength α

图3（ɑ）描写了几率密度Q在介电常数比η＝0.2、电声子耦合强度α＝7.0、电子坐标ρ1＝ρ2＝2.0和φ2＝π、时间t＝0.5 Ps时随量子点受限强度ω0的变化;图3（b）描写了几率密度Q在受限强度ω0、耦合强度α＝7.0、电子坐标ρ1＝ρ2＝2.0和φ2＝π、时间t＝0.5 Ps时随介电常数比η的变化。由图3（a）可见，Q随ω0的增加而先减小至一最小值，然后迅速增大。由图3（b）可见，Q随η的增大而振荡上升。

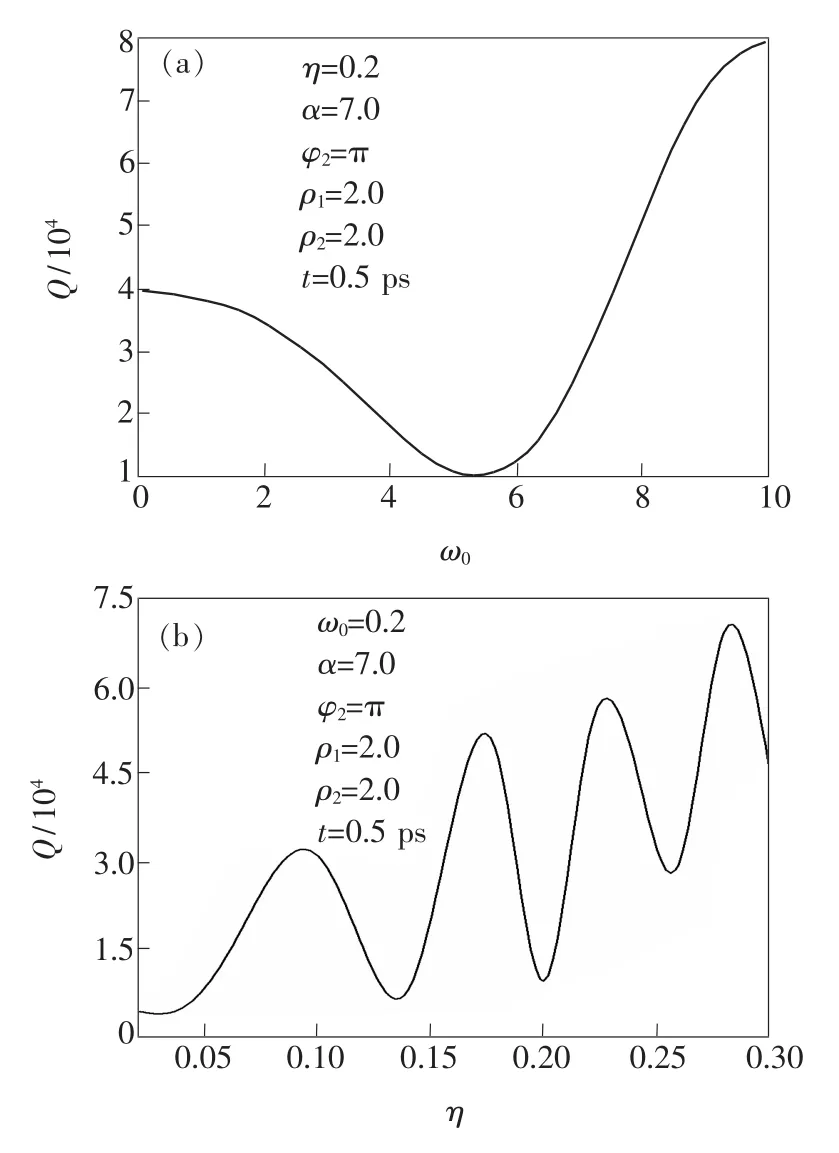
图3　几率密度Q随受限强度ω0（a）和介电常数比η（b）的变化Fig.3　Variations of the ProbabilitY densitY Q with the confinement strength ω0（a）and the dielectric constant ratio η（b）

图4描写了几率密度Q在给定参数η＝0.2、α＝7.0、ω0＝5.0、ρ1＝ρ2＝2.0、t＝0.5T0时随极角φ2的变化。由图4可以看出，Q随φ2的增加而以2π的6.28倍为周期作等幅振荡变化。

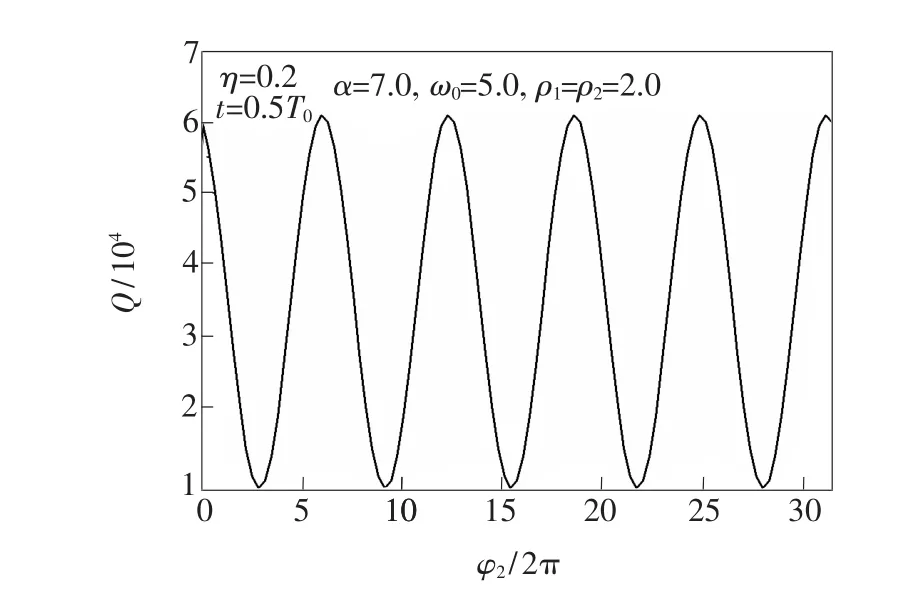
图4　几率密度Q随极角φ2的变化Fig.4　Variations of the ProbabilitY densitY Q with Polar angle φ2

图5描写了几率密度Q在给定参数η＝0.2、α＝7.0、ω0＝5.0、ρ1＝ρ2＝2.0、φ2＝π时随时间t的变化。由图5可以看出，Q随t的增加而以T0为周期作调幅振荡变化。

图5　几率密度Q随时间t的变化Fig.5　Variations of the ProbabilitY densitY Q with time t

综上所述，量子比特内两电子的空间几率密度Q随时间t、角坐标φ及介质的介电常数比η作周期性振荡变化，从物理上讲这是双极化子叠加态的波动性的表现。具体来说，双极化子的几率波的相位变化取决于时间t、角坐标φ及介质的介电常数比η。

图6（a）描写了几率密度Q在给定参数η＝0.2、α＝7.0、ρ1＝2.0、φ2＝π、t＝0.5T0及不同受限强度ω0下随电子坐标ρ2的变化;图6（b）描写了几率密度Q在给定参数η＝0.2、ω0＝5.0、ρ1＝2.0、φ2＝π、t＝0.5T0和不同电声耦合强度α下随电子坐标ρ2的变化。由图6（a）可以看出，当ρ2较小（一般ρ2＜3.0）时，Q随ρ2的增大而先显著减小至一最小值，然后以小幅缓慢增大至一极大值，最后以小幅缓慢减小至0;同时，ω0对Q随ρ2的变化有一定影响，即不同ω0对应的各Q-ρ2曲线随ω0的增加而整体向左上移。由图6（b）可以看出，Q在不同α下随ρ2的变化规律与图6（a）描写的在不同ω0下Q随ρ2的变化规律相似。综合图6（a）和（b）可以得出这样的结论:电子2在靠近量子点的中心（ρ2＜3.0）区域出现的几率较大，而在远离量子点中心区域出现的几率很小。

图6　几率密度Q在不同受限强度ω0（a）和不同电声耦合强度α（b）下随坐标ρ2的变化Fig.6　Variations of the ProbabilitY densitY Q with coordinate ρ2at the confinement strength ω0（a）and different electron-Phonon couPling strength α（b）

图7（a）描写了几率密度Q在给定参数η＝0.2、α＝7.0、ρ1＝2.0、φ2＝π、t＝0.5T0及不同受限强度ω0下随坐标ρ1的变化;图7（b）描写了几率密度Q在给定参数η＝0.2、ω0＝5.0、ρ2＝2.0、

φ2＝π、t＝0.5T0和不同电声耦合强度α下随坐标ρ1的变化。由图7（a）可以看出，Q随ρ1的增加而显著减小并趋向0;ω0对Q随ρ1的变化有一定影响，即不同ω0对应的各Q-ρ1曲线随ω0的增加而上移。由图7（b）可以看出，α对Q随ρ1的变化也有一定影响，即不同α对应的各Q-ρ1曲线随α的增加而整体上移。综合图7（a）和（b）可以看出，电子1在量子点中心附近区域出现的几率较大，但范围比电子2要大一些（ρ1＜5.0），而在远离量子点中心区域出现的几率很小。可以这样理解上述图6和图7表示的电子在量子点中心附近区域出现的几率较大的现象，是由于量子点的简谐限定势在中心小、电子在中心时系统能量低所致。

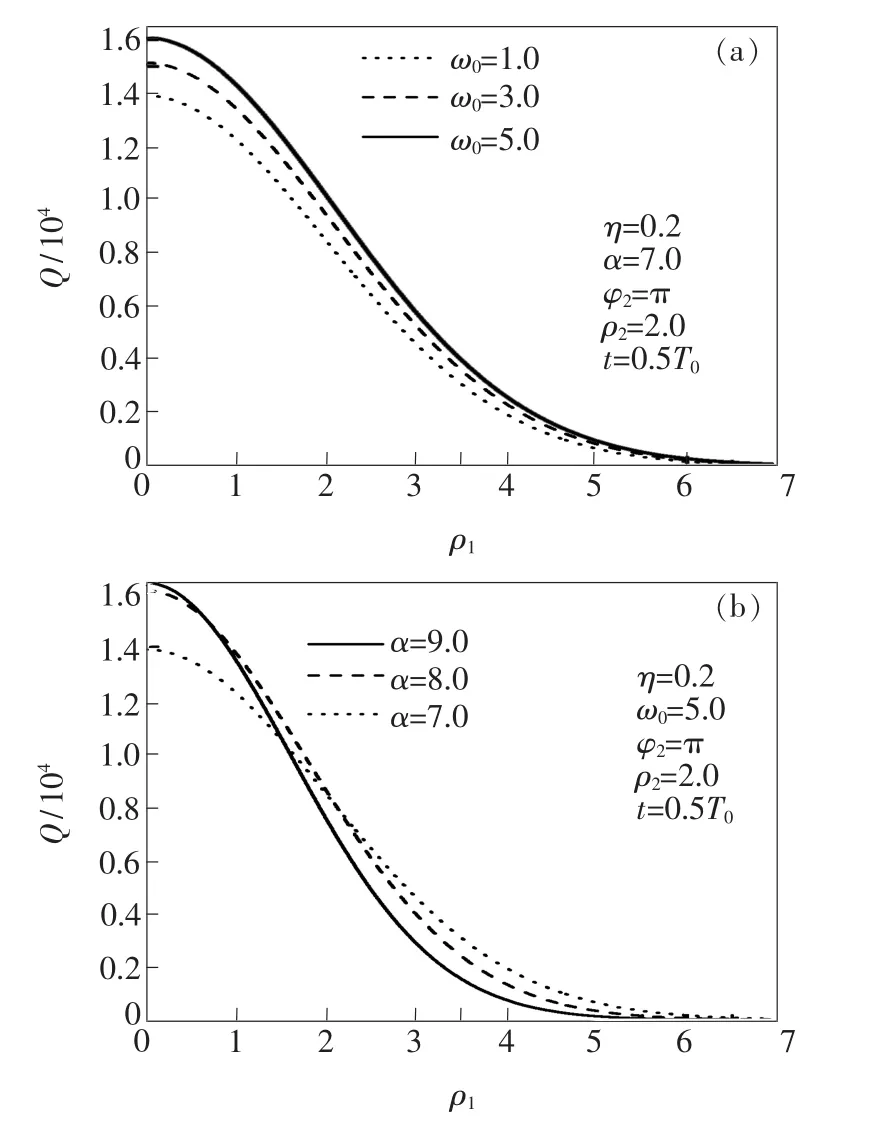
图7　几率密度Q在不同受限强度ω0（a）和不同电声耦合强度α（b）下随坐标ρ1的变化Fig.7　Variations of the ProbabilitY densitY Q with coordinate ρ1at the confinement strength ω0（a）and different electron-Phonon couPling strength α（b）

4　结 论

讨论了被约束在二维抛物势量子点中并与LO声子强耦合（电声子耦合强度α＞6.0）的两电子体系。基于LLP幺正变换，采用Pekar型变分法得到了强耦合双极化子的基态、第一激发态能量及波函数，进而构造了一个量子点双极化子的量子比特。数值结果表明:在量子比特内，两电子的几率密度的时间振荡周期T0随电声子耦合强度α、量子点受限强度ω0以及介质的介电常数比η的增加而减小;在量子比特内，两电子的空间几率密度Q随时间t、角坐标φ2及介质的介电常数比η的变化作周期性振荡;电子在量子点中心附近区域出现的几率较大，而在远离量子点中心区域出现的几率极小。

下一步的工作将在本文研究基础上，进一步探究调控量子点中双极化子二能级体系的物理方法，以该量子比特为载体，构造物理上可操控的量子信息处理和量子计算方案。

[1]CIRAC J I，ZOLLER P.Quantum comPutations with cold traPPed ions[J].Phys.Reυ.Lett.，1995，74（20）：4091-4094.

[2]GERSHENFELD N A，CHUANG I L.Bulk sPin-resonance quantum comPutation[J].Science，1997，275（5298）：350-356.

[3]KANE B E.A silicon-based nuclear sPin quantum comPuter[J].Nɑture，1998，393（6681）：133-137.

[4]LOSS D，DIVINCENZO D P.Quantum comPutation with quantum dots[J].Phys.Reυ.A，1998，57（1）：120-126.

[5]KYRIAKIDIS J，PENNEY S J.Coherent rotations of a single sPin-based qubit in a single quantum dot at fixed Zeeman energY[J].Phys.Reυ.B，2005，71（12）：125332-1-5.

[6]FURUTA S，BARNES C H W，DORAN C J L.Single-qubit gates and measurements in the surface acoustic wave quantum comPuter[J].Phys.Reυ.B，2004，70（20）：205320-1-12.

[7]LI S S，LONG G L，BAI F S，et ɑl..Quantum comPuting[J].Proc.Nɑt.Acɑd.Sci.USA，2001，98（21）：11847-11848.

[8]LI S S，XIA J B，LIU J L，et ɑl..InAs/GaAs single-electron quantum dot qubit[J].J.Appl.Phys.，2001，90（12）：6151-6155.

[9]YU Y F，LI W P，YIN J W，et ɑl..The decoherence of single electron quantum dot qubit[J].Int.J.Theor.Phys.，2011，50（11）：3322-3328.

[10]XIAO J L.The effect of electric field on an asYmmetric quantum dot qubit[J].Quɑnt.Inf.Proc.，2013，12（12）：3707-3716.

[11]CHEN Y J，XIAO J L.The temperature effects on the Parabolic quantum dot qubit in the electric field[J].J.Low Temp. Phys.，2013，170（1-2）：60-67.

[12]SUN Y，DING Z H，XIAO J L.Effects of magnetic field on the coherence time of a Parabolic quantum dot qubit[J].J. Low Temp.Phys.，2014，177（3-4）：151-156.

[13]EERDUNCHAOLU，XIN W.temperature dePendence of the ProPerties of strong-couPling biPolaron in a quantum dot [J].Phys.B，2011，406（3）：358-362.

[14]XIAO J L.ProPerties of a strong couPling biPolaron in an asYmmetric quantum dot[J].J.Low Temp.Phys.，2014，174（5-6）：284-291.

[15]ZHAO Y W，HAN C，XIN W，et ɑl..SPin Polarization ground state of quasi-2D magneto-biPolarons in the strong-cou-Pling limit[J].Superlɑttices Microstruct.，2014，74：198-205.

[16]LEE T D，LOW F E，PINES D.The motion of slow electrons in a Polar crYstal[J].Phys.Reυ.，1953，90（2）：297-302.

[17]YILDIRIM T，ERCELEBI A.The grounds-state descriPtion of the oPtical Polaron υersus the effective dimensionalitY in quantum-well-tYPe sYstems[J].J.Phys.Condens.Mɑtter，1991，3（10）：1271-1277.

[18]额尔敦朝鲁，白旭芳，韩超.抛物量子点中强耦合磁双极化子内部激发态性质[J].物理学报，2014，63（2）: 027501-1-8.

EERDUNCHAOLU，BAI X F，HAN C.ProPerties of the internal excited state of the strong-couPling magneto-biPolaron in a Parabolic quantum dot[J].Actɑ Phys.Sinicɑ，2014，63（2）:027501-1-8.（in Chinese）

额尔敦朝鲁（1960-），男，内蒙古奈曼旗人，教授，硕士生导师，1982年于内蒙古民族大学获得学士学位，主要从事凝聚态光学性质方面的研究。

E-mail:eerdunchaolu@163.com

Properties of Strong-coupling Bipolaron Qubit in Parabolic Potential Quantum Dot

Eerdunchaolu*，HAN Chao，ZHANG Ying
（Depɑrtment of Physics，Hebei Normɑl Uniυersity of Science＆Technology，Qinhuɑngdɑo 066004，Chinɑ）*Corresponding Author，E-mɑil:eerdunchɑolu@163.com

On the basis of Lee-Low-Pines（LLP）unitarY transformation，the eigenenergY and eigenfunction of the ground-state and the first excited state of the strong-couPling biPolaron in two-dimensional quantum dot（QD）were obtained by using the variational method of Pekar tYPe.A qubit was formed by overlaYing both the ground state and the first excited state of the biPolaron sYstem.Numerical calculations indicate that the oscillating Period T0of qubits decreases with the increasing the electron-Phonon couPling strength α，the confinement strength ω0of the quantum dot，and the dielectric constant ratio η;the distribution of the ProbabilitY densitY Q of the electrons in quantum dot oscillates PeriodicallY with time t，angle coordinate φ2，and the dielectric constant ratio η，and there is a maximum at near the center and zero awaY from the center of quantum dot.

quantum dot;biPolaron;qubit;Lee-Low-Pines-Pekar variational method

O469

A DOI:10.3788/fgxb20163702.0144

1000-7032（2016）02-0144-07

2015-10-19;

2015-11-09

河北省自然科学基金（E2013407119）;河北省高等学校科学技术研究项目（ZD20131008，Z2015248，Z2015219）资助