基于MapReduce的K-means聚类算法的优化
2016-10-28孙玉强李媛媛
孙玉强,李媛媛,陆 勇
(常州大学 信息科学与工程学院,江苏 常州 213164)
基于MapReduce的K-means聚类算法的优化
孙玉强,李媛媛,陆 勇
(常州大学 信息科学与工程学院,江苏 常州 213164)
针对传统的聚类算法K-means对初始中心点的选择非常依赖,容易产生局部最优而非全局最优的聚类结果,同时难以满足人们对海量数据进行处理的需求等缺陷,提出了一种基于MapReduce的改进K-means聚类算法。该算法结合系统抽样方法得到具有代表性的样本集来代替海量数据集;采用密度法和最大最小距离法得到优化的初始聚类中心点;再利用Canopy算法得到粗略的聚类以降低运算的规模;最后用顺序组合MapReduce编程模型的思想实现了算法的并行化扩展,使之能够充分利用集群的计算和存储能力,从而适应海量数据的应用场景;文中对该改进算法和传统聚类算法进行了比较,比较结果证明其性能优于后者;这表明该改进算法降低了对初始聚类中心的依赖,提高了聚类的准确性,减少了聚类的迭代次数,降低了聚类的时间,而且在处理海量数据时表现出较大的性能优势。
K均值算法;抽样;Canopy算法;最大最小距离法
0 引言
随着数据规模的爆炸性增长,传统的数据挖掘工作在处理大规模数据时会出现用时过长、存储量不足等缺点。云计算的提出将这些问题迎刃而解,它是一种基于互联网的计算,是分布式计算、并行处理和网格计算的进一步发展。由Google提出的MapReduce编程框架[1]是云计算中代表性的技术,主要用于海量数据的并行计算。已有多种数据挖掘算法在MapReduce计算模型的基础上被实现了,而聚类是在数据挖掘中运用比较广泛的一种算法。
K-means算法是一种典型的基于划分的聚类算法[2],该算法简单高效,运用于科学研究的各个领域。但是它对初始聚类中心的选择非常敏感,不能有效地对大规模数据进行聚类处理。针对 K-means算法的特点以及不足,很多学者提出了相应的改进K-means算法。邓海等人[3]提出了基于最近高密度点间的垂直中心点优化初始聚类中心的K-means聚类算法;王玲等人[4]提出一种密度敏感的相似度度量的方法;马帅等人[5]提出了一种基于参考点和密度的快速聚类算法。这些研究通过不同的方法解决了算法对初始中心敏感的问题,但却增加了算法的复杂度。其他的例如毛典辉等人[6]提出了改进的Canopy和K-means相结合的算法;虞倩倩[7]等人提出了聚类的蚁群优化算法;马汉达等人[8]提出了基于粒子群算法(PSO)的K-means算法;贾瑞玉等人[9]提出了并行遗传K-means聚类算法,都是结合一些成熟的算法来改进K-means聚类算法,虽然在少量数据环境下能够显著提升K-means算法的性能,但却因为额外的组件增加了算法的复杂性, 无法适应海量数据的处理需求。因此,本文提出了一种基于MapReduce的高效 K-means并行算法, 其结合了抽样方法进行预处理以减少数据量;通过密度思想对初始中心点优化提高聚类准确性;结合其他算法降低计算规模;再通过MapReduce分布式并行模型提高运行效率。实现的过程主要有4个子任务:1)抽取样本;2)计算样本初始聚类中心点;3)Canopy划分;4)K-means迭代。通过实验结果得出,此改进算法在处理海量数据时可以体现出更大的优势。
1 背景
1.1 MapReduce简介
MapReduce是一种分布式并行编程模型,数据被存储在分布式文件系统(distributed file system, DFS)中,以键-值对

图1 Mapreduce的操作流程图
1.2 密度思想
在一个大规模的数据对象空间中,低密度区域的数据对象点一般划分着高密度区域的数据对象点,通常所说的噪声点或孤立点就是这些低密度区域的点。如果在进行聚类分析时,这些噪声点或孤立点被选为初始聚类中心,就会造成聚类不理想的结果。因此,初始聚类中心的选取应该集中到高密度区域以排除孤立点的干扰。为了有效地排除数据样本中存在的噪声点对象和孤立点对象,可以通过引入高密度点的概念来处理。
定义1 高密度点:取数据集中的数据对象xi为中心点,计算此中心点在邻域半径δ内包含的样本个数,若样本个数不少于常数Minds,则该中心点就被称为高密度点。其中δ的取值需结合输入的数据对象集,将其取为n个数据样本间距离均方根的一半,公式如下:
(1)
其中:‖xi-xj‖为公式(2)的欧式距离D(i,j)。
1.3 最大最小原则
为了避免初值选取时出现的聚类中心过于邻近的情况,最大最小原则可以用来选取尽可能远的数据对象作为初始聚类中心。“最大最小原则”[11]的算法描述如下:
1)从n个数据集{X1,X2,…Xn}中随机选取一个样本作为第一个初始聚类中心点C1;
2)在剩余的数据对象集中找到距离C1最远的点,作为第二个初始聚类中心点C2;
3)分别计算剩余的数据对象集到已有的i个聚类中心点之间的距离,取最小距离的最大者:D(i+1)=max{min{D(j,1),D(j,2),…,D(j,i)}},j=1,2,…,n,则第i+1个初始聚类中心点为Ci+1=Xj;
4)用来表示D(i+1)变化幅度的深度指标Depth(k)可以通过边界识别的思想进行引入,其定义为:Depth(k)=|D(k)-D(k-1)|+ |D(k+1)-D(k)|,当深度值 Depth(k)取得最大值时,需求解的最优初始聚类中心点就为前k个记录值,同时下一轮Canopy的区域半径可设为T1=D(k),避免了Canopy算法初始值设置的盲目性和随机性。
1.4 Canopy算法
Canopy算法[12]的思想是使用一种代价低的相似性度量方法,快速粗略地将数据划分成若干个重叠子集,每个子集可以看成是一个簇。Canopy算法基本流程[13]如下:
1)设置阈值T1,T2,其中T1>T2;
2)从数据集中取得一个数据对象,构建初始Canopy,并从该数据集中删除该数据对象;
3)从剩余的数据集中取出一个数据对象,
计算其与所的有Canopy中心之间的距离,如果该数据对象与某个Canopy中心的距离在T1内,则将该对象加入到这个Canopy中,如果该对象与Canopy中的某个Canopy中心的距离小于T2,则当该数据对象与所有Canopy中心的距离计算完成后,将其从数据集中删除,如果该数据对象没有加入到任何Canopy,则构建一个新的Canopy;
4)重复步骤3),直到数据集为空。
2 K-means算法介绍和分析
2.1 K-means算法思想
K-means算法流程[14]:1)首先从n个数据对象中随机选取k个初始聚类中心点;2)对于剩下的其它数据对象,分别求它们与这k个聚类中心的欧式距离(相似度),将它们分配给与其欧式距离最小(相似度最大)的聚类;3)计算新的聚类中心(聚类中所有对象的均值);4)不断重复步骤2)和3)这一过程直到准则函数开始收敛为止。
1)欧式距离公式如下:
(2)
其中:i=(xi1, xi2,...,xip);j=(xj1,xj2,...,xjp);它们分别表示一个p-维数据对象。
2)均方差准则函数
(3)
其中:E为数据集中所有数据的均方差之和;p为数据对象空间中的一个点;mi为聚类Ci的均值(p和mi都是多维的)。
2.2 K-means算法的不足及其改进
1)传统K-means算法不能有效处理大规模数据的聚类操作。而基于MapReduce的分布式并行计算模型,将一个大型数据切分成多个小数据模块的形式,分配给多台计算机集群进行分布式计算,与传统的单机运行平台相比,加快了总体的运行速率,减少了执行时间。
2)传统的K-means算法通过完全随机的策略对初始聚类中心点进行选取,不能确保聚类结果的准确性,更不能有效处理海量数据。可以通过抽样方法对初始数据进行预处理操作,得出有效样本集合。再结合密度思想和最大最小原则求得样本集的初始聚类中心。在高密度区域选择初始中心点可以排除噪声点和孤立点的干扰,而最大最小原则可以避免在高密度区域选取的中心点过于邻近。
3)传统的K-means算法在比较数据对象与聚类中心的距离时,计算了全局对象与中心点之间一一对应的距离,虽然在一定程度上确保了聚类的效果,但是总体上降低了算法的效率,而且不能适应大规模数据的聚类处理。对此,引入了Canopy(华盖)的思想,每次只比较落在同一Canopy内的对象与相应中心点之间的距离,通过减少比较次数大大降低整个聚类的运行时间[13]。实验结果表明,该策略在处理大规模数据时,与传统方法相比,其收敛速度更快。
3 改进K-means算法的并行化
改进的K-means算法思想:首先采取系统抽样,得到一个具有较少数目并能代表全局数据对象的样本集合;再运用密度法和最大最小距离法相结合的方法求得样本集合的最佳初始聚类中心;最后利用Canopy算法对全局数据对象进行粗略划分,以改进 K-means 算法。一方面,该算法可以通过获得优化的初始聚类中心来提高聚类结果的精确度;另一方面,该算法能够智能的降低数据比较的次数。最后,将改进后的算法运用于MapReduce的并行计算模型中,其基本流程如图2所示。
3.1 抽取样本
系统抽样主要将在HDFS上存储的split文件块进行规则设计与文件读取,设每个部分抽样概率为px,则我们首先在Map阶段对每个文件块的数据量大小以及文件行数进行预估,顺序读取文件的前x%行,并指定为相同的key值传到同一个Reducer上,在Reduce阶段对每个块的样本数据合并,得到最终的抽样结果。
指定参数0<ε<1来控制样本大小,设n为数据集大小,则通过概率px=1/(nε2)对整个数据集进行系统抽样,可以得到均匀的样本。算法1描述了利用MapReduce模型进行系统抽样(RS)的过程。
算法1:系统抽样算法。
输入:初始数据集G;
输出:样本集S。
Map 函数:
1)每个Map读取数据G和抽样概率px,利用px进行抽样;
2)将所有数据作为value,为它们指定相同的key,形成中间键值对;
Reduce 函数:
1)将中间键值对shuffle到同一Reducer上;
2)输出样本数据集S;
3.2 计算样本初始聚类中心点
3.2.1 计算高密度数据集
算法2:高密度点生成的并行化。
输入:样本集S。
输出:高密度点集HD。
Map函数:
1)每个Map读取样本集S,计算每个样本点xi与其余样本点之间的距离D(i,j);
Reduce函数:
(1)根据公式(3)计算邻域半径δ,并统计到每个样本点xi距离小于δ的样本个数;
2)读取密度阈值Minds,若个数大于Minds,则把该点定义为高密度点,得到高密度点集合HD。
3.2.2 计算优化初始中心点
算法3:样本中心点生成算法。
Map 函数:
输入:高密度点集HD;
输出:中心点的初始集合Q。
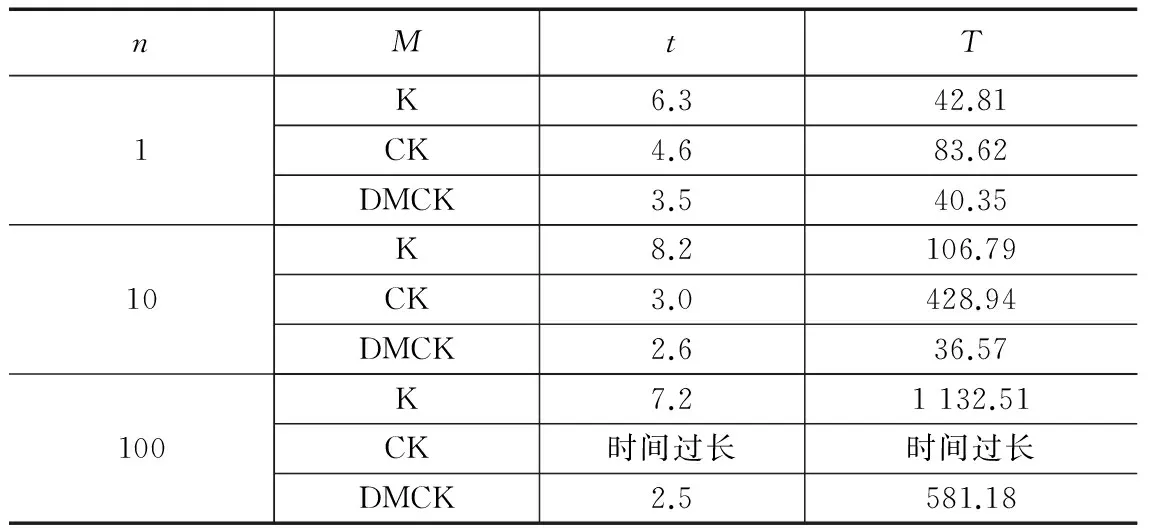
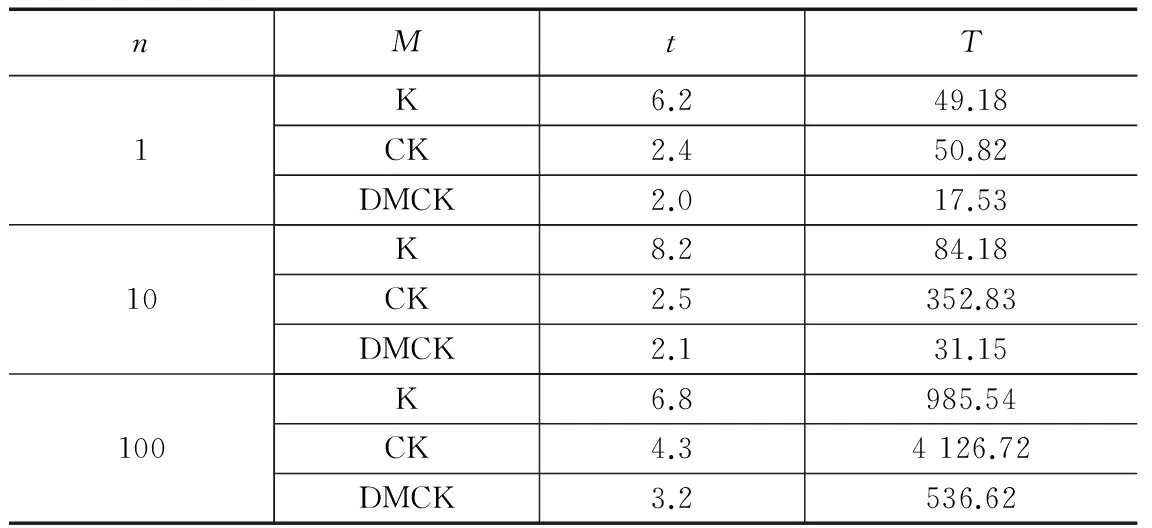
(1)设置初始中心点的集合,Q=null;
(2)设置迭代次数,Whilek (3)if集合Q为空,求数据集V(当前节点数据集V)中密度最大点,并保存该点至集合Q;else求数据集V中数据点与集合Q中数据点的距离最小值中最大者,并保存该点至集合Q; Reduce函数: 输入:各节点中心点的初始集合Q={Q1,Q2,…,Qn}; 输出:样本中心点的最终集合U以及半径T1; (1)求取集合Q的数据总量,N=Count(Q); (2)设置迭代次数,While k< sqrt(N); (3)求数据集中数据点之间距离最小值中最大者,并保存该点至集合Q′; (4)求取集合Q′的数据量m=Count(Q′); (5)whilej 3.3 Canopy划分 算法4:Canopy划分算法。 Map函数: 输入:初始数据集G; 输出:标注对应Canopy的数据集C。 (1)读取样本中心点的最终集合U以及半径T1,计算初始数据集与样本中心点之间的距离D; (2)当D<=T1,则标注该数据点属于对应的Canopy,并将结果输出。 3.4 K-means迭代 该阶段的主要任务是进行精确的聚类计算,其算法流程为: 算法5:K-Means算法。 输入:标注对应Canopy的数据集C; 输出:K中心点集合U′。 Map函数: 1) 读取样本中心点的最终集合U,将样本中心点的最终集合U作为初始K中心点集合,U′=U; 2)通过Map函数比较已标注的输入数据点与对应中心点的距离,输出当前数据点及对应最近距离的中心点编号; Reduce函数: 1)通过Reduce函数将同一中心点下的数据点归并,计算均值并将结果输出作为新的中心点; 2)判断准则函数是否收敛,若收敛则终止程序,否则进行下一轮MapReduce的迭代。 本实验在Hadoop分布式集群平台上对多组测试数据进行了仿真测试[15],传统的K-means算法K:任意选取k个聚类中心点后再用K-means算法进行聚类;改进的Canopy-Kmeans算法CK:首先结合最大最小原则计算出初始k个Canopy中心点,利用各个Canopy中心点对数据集进行粗略地Canopy聚类,再结合K-means算法对每个Canopy类进行精确地聚类;高效的DM Canopy-Kmeans(Canopy-Kmeans Clustering Algorithm based on Density Method and Max-min Distance Algorithm)算法DMCK:1)结合密度法和最大最小距离法计算已有的抽样数据对象的k个初聚类中心C;2)利用样本聚类中心C作为全局数据对象的初始聚类中心,结合Canopy算法进行Canopy划分;3)再利用 K-means算法计算出最终的聚类结果。数据集的记录数为n,聚类个数为k,具体算法为M,迭代次数为t,算法执行时间为T。 实验一:验证改进的K-means算法的可行性。 实验说明:采用50条测试数据进行测试,运行结果见表1。 表1 不同聚类算法和不同聚类个数的聚类结果 从表1可以得出以下结论,改进的Canopy-Kmeans算法运行的聚类结果与高效的DM Canopy-Kmeans算法的聚类结果相比,其迭代次数和运行时间取得了相似的结果,而且保持了稳定性;且改进的Canopy-Kmeans算法与传统的随机选择聚类中心的K-means算法相比,表现出了更好的性能优势。但在处理海量数据时,若用改进Canopy-Kmeans算法,聚类迭代次数会增加,甚至会造成内存不足。所以提出了这种折中的用样本数据初始聚类中心代替全局数据初始聚类中心的聚类算法。 实验二:验证改进的K-means算法的有效性。 实验说明:用随机产生的记录数来验证方法的有效性,记录数n(单位:万)分别是1、10、100,环境:单机伪分布条件下,聚类方法同上,聚类个数为100时结果见表2。 表2 单机下的聚类结果 通过表2得出以下结论:改进的Canopy-Kmeans聚类算法在用最大最小原则计算初始聚类中心点时,随着处理的数据规模的扩大,迭代时间也会随之增长,会导致算法效率变低。当处理的数据量不断增加时,这种改进的聚类算法将不再适用于初始中心点的计算。而提出的高效DM Canopy-Kmeans算法在面对海量数据量时,大大减少了执行的时间,提高了算法的运行效率和聚类的精度。 实验三:验证改进算法可以并行执行。 实验说明:4台均是装有Centos5操作系统的虚拟机,其中一台是master,剩余三台是slave,内存512 M,硬盘100G,2.5Ghz双核CPU。数据:使用实验2中数据,在集群平台下聚类为100时的运行结果见表3。 表3 集群下运行结果 表3与表2对比得出以下结论,在同样的条件下,并行化与串行相比,其操作时间明显是降低的,且提高了算法的运行效率,进一步体现了海量数据在集群环境下处理的优势。 在处理海量数据时,为减少 k-means 算法对初值的依赖性, 我们详细探讨了初始聚类中心的优化选择问题,并提出全新的 DM Canopy-Kmeans 算法。为提高算法的运行效率,在MapReduce的平台下对改进聚类算法进行实现。并通过实验对其进行对比分析,验证了基于并行模型下的改进算法更优于传统的算法,提高了算法的执行效率。下一步的主要工作是进一步改进抽样数据的样本质量,可以用来更精确地代表全局数据对象。 [1] Dean J, Ghemawat S. MapReduce: simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113. [2] Han J, Kamber M. Data Mining: Concepts and Techniques [M]. Fan Ming, Meng Xiaofeng, translation.2 edition. Beijing: Mechanical Industry Press, 2007. [3] 邓 海,覃 华,孙 欣.一种优化初始中心的K-means 聚类算法[J].计算机技术与发展,2013, 23(11):42-45. [4] 王 玲,薄列峰,焦李成.密度敏感的普聚类[J].电子学报,2007, 35(8) : 1577-1581. [5] 马 帅,王腾蛟,唐世渭,等.一种基于参考点和密度的快速聚类算法[J].软件学报,2003,14(6):1089-1095. [6] 毛典辉.基于MapReduce的Canopy-Kmeans改进算法[J].计算机工程与应用,2012,48(27):22-26. [7] 虞倩倩,戴月明,李晶晶.基于MapReduce的ACO-K-means并行聚类算法[J].计算机工程与应用,2013,49(16):117-120. [8] 马汉达,郝晓宇,马仁庆.基于Hadoop的并行PSO-kmeans算法实现Web日志挖掘[J].计算机科学,2015,42(6A):470-473. [9] 贾瑞玉,管玉勇,李亚龙.基于MapReduce模型的K-means并行遗传聚类算法[J].计算机工程与设计,2014,35(2):657-660. [10] Isard M, Budiu M, Yu Y, et al. Dryad: Distributed data-parallel programs from sequential building blocks[A]. Proc. of the 2ndEuropean Conf. on Computer Systems (EuroSys)[C]. 2007:59-72. [11] 刘远超,王晓龙,刘秉权.一种改进的 K-means 文档聚类初值选择算法[J].高技术通讯,2006(1):11-15. [12] 孙吉贵,刘 杰,赵连宇.聚类算法研究[J].软件学报,2008, 19(1):48-61. [13] 李应安.基于MapReduce的聚类算法的并行化研究[D].广州:中山大学,2010. [14] Han Jiawei. Kamber. Data mining: Concepts and techniques [M]. Beijing: Mechanical Industry Press. 2008: 288-375 (in Chinese). [15] Apache.Hadoop[EB/OL].[2012-10-10].http: //hadoop.apache.org. Optimization of K-means Clustering Algorithm Based on MapReduce Sun Yuqiang, Li Yuanyuan, Lu Yong (School of Information Science&Engineering, ChangZhou University, Changzhou 213164,China) To deal with the problems that traditional K-means clustering algorithm is very dependent on the selection of the initial points, being prone to clustering result of local optimum rather than global optimum, and it is difficult to meet the need of dealing with massive amounts of data, an improved K-means clustering algorithm based on MapReduce is proposed. The algorithm combines systematic sampling method to get a representative sample set which is used to replace the massive data set; and uses density method and Max-Min distance method to get the optimal initial clustering centers; and adopts Canopy algorithm to get a rough clustering which can reduce the computational scale; and finally employs the idea of sequential composition of MapReduce programming model to realize the parallel extension of the algorithm, which can make full use of the computing and storage capacity of the cluster, in order to adapt to the application of massive data. The improved algorithm is compared with the traditional clustering algorithms in this paper, and the comparative results show that the performance of improved algorithm is better than the latter. The experiments show that the improved method reduces the dependence on the initial cluster centers and also reduces the number of iterations of clustering and the clustering time.Furthermore it shows greater performance advantage in dealing with massive data. K-means clustering algorithm;sampling; Canopy algorithm;Max-Min distance method 2016-01-19; 2016-02-29。 国家自然科学基金项目(11271057,51176016);江苏省自然科学基金项目(BK2009535)。 李媛媛(1991-),女,江苏盐城人,硕士研究生,主要从并行计算、数据挖掘等方向的研究。 孙玉强(1956-),男,河南人,教授,硕士研究生导师,主要从事并行计算、软件工程等方向的研究。 1671-4598(2016)07-0272-04 10.16526/j.cnki.11-4762/tp.2016.07.073 TP311 文献标识码:A4 实验结果

5 结束语
