基于FPFH特征的三维场景重建

艾 达，王 苗，倪国斌

(1.西安邮电大学 公安部电子信息勘查应用技术重点实验室，西安 710121)2.西安邮电大学 通信与信息工程学院，西安 710061)

基于FPFH特征的三维场景重建

艾 达1，王 苗2，倪国斌2

(1.西安邮电大学 公安部电子信息勘查应用技术重点实验室，西安 710121)2.西安邮电大学 通信与信息工程学院，西安 710061)

文章在阐述不同视角下在对一对三维点云数据集两两配准的基础之上，针对ICP精确匹配算法须使初始点云收敛否则无法获取准确匹配结果的问题，提出了基于FPFH特征描述子的特征点云粗匹配;调整两片点云的初始位置，为ICP算法提供了良好的初始位置进一步提高点云的匹配精度;并且在此基础上通过大量实验得到点云对应点对之间的最大距离与拟合系数的函数关系，得到粗匹配最优值，进而得到最佳配准效果。实验证明通过粗匹配最高能将匹配拟合系数提高60.3%。

两两配准;FPFH特征;粗匹配

0 引言

三维场景重建(three-dimensional scene reconstruction)技术[1]在三维视觉领域快速发展并流行的一门新技术，通过计算机数字化手段，将客观世界中的三维实体真实再现在计算机中，是计算机视觉、人工智能、虚拟现实、人机交互等前沿领域的热点和难点,与传统的通过图片等二维图像，利用先验知识从物体的二维信息中推断出三维模型的建模技术相比，其在重建效率、精度和实时性方面都有很大提高。

点云配准作为三维重建技术的关键技术之一，能将多角度下获取的点云，变换到同一坐标系下[2]。文献[3]在基于传统四元数算法的基础上提出迭代最近点(iterative closest points)ICP算法。文献[4]对文献[3]进行改进，通过特征度量建立迭代优化函数。文献[5]提出基于GPU的KinectFusion重建技术，文献[6]利用测量得到的横向和纵向噪声分布，应用于KinectFusion系统体融合及管道内姿态估计，得到精细模型重建。文献[7]提出运动恢复结构(structure from motion，SFM)算法，在摄像机定位和稀疏表面重建重建效果精确。

这些算法被提出之后，很快广泛的应用到三维重建的领域中，取得了一些成果[8],但是对于透明物体和平面物体的重建效果并不是很好，因此文章在前人研究的基础上，介绍了迭代最近点(iterative closest points)ICP算法通过配准和融合将获得的深度图像合并起来[9]，但是ICP算法要求待配准的点云具有较好的初始位置，否则难以获得较好的匹配效果。因此在ICP精匹配之前，应先对点云进行粗配准，调整两片部分重叠点云的初始位置。在对点云的粗配准的计算过程中，首先计算两幅图像的关键点，其次计算其关键点处快速点特征直方图描述子(FPFH)[10],然后提取三组随机点对，计算点对之间的转换关系，将该对应关系应用于所有点对的转换，最后设置阈值，得到最佳的转换关系。

1 三维场景重建及其步骤

图1是三维重建流程图，首先利用激光扫描仪[11]或三维相机[12]等获取三维景深数据。其次进行点云预处理，消除由于设备精度、环境因素等点云数据中的噪声点，滤波作为点云处理流程的第一步，对后续处理管道影响很大。对滤波后的点云进行下采样能在不影响精度的情况下，简化点云数量，提高匹配效率。再次，对得到的点云进行配准[13]，先求取三维数据的法线信息，然后利用其法线信息提取一对点云的FPFH特征，最后使用采样一致性初始匹配算法(SAC-IA算法)获取点云的初始变换矩阵，在粗匹配的基础上进行ICP精确配准。最后使用贪婪投影三角化算法对点云进行三角化得到重建表面。

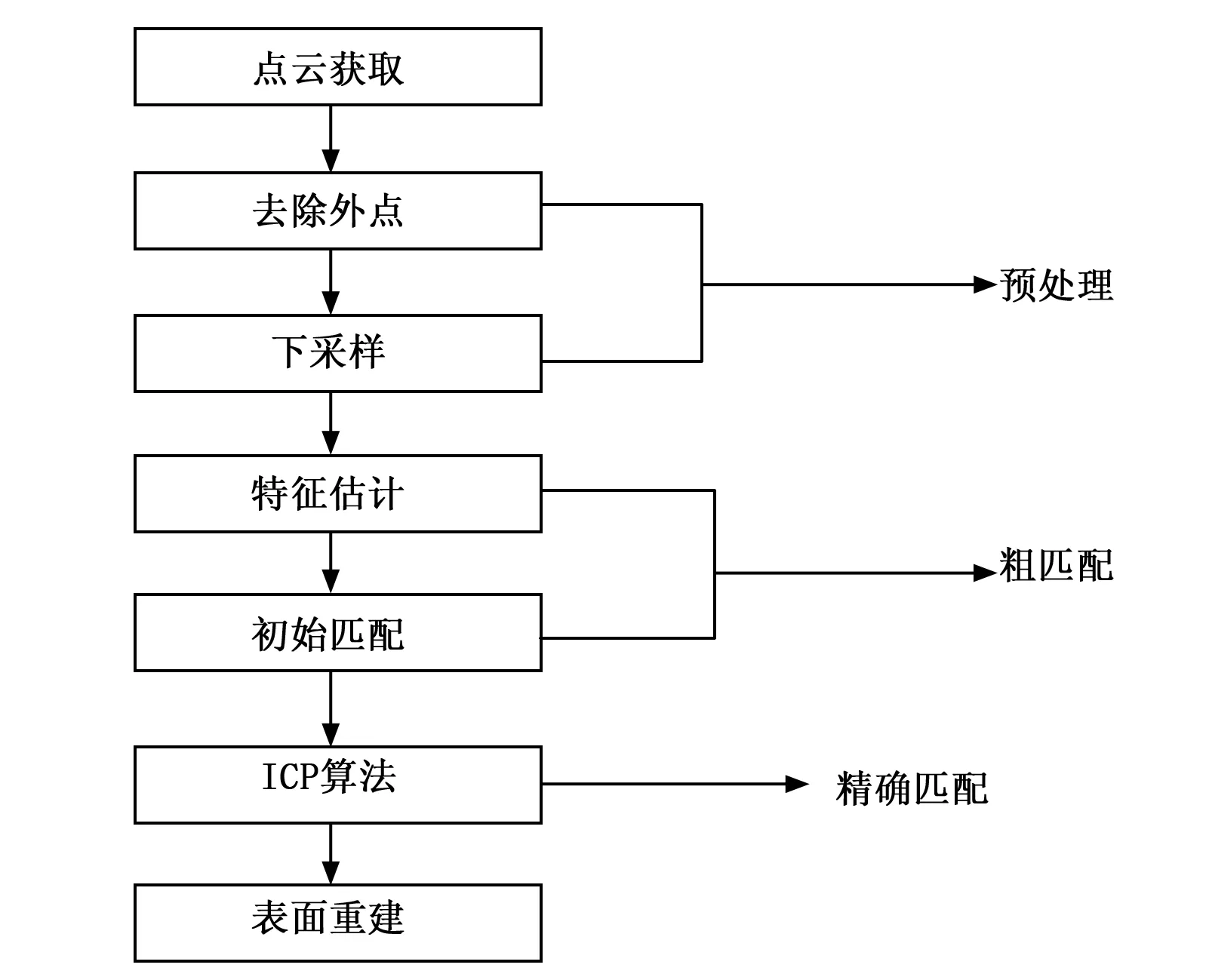
图1 三维重建流程图

2 点云匹配算法

在实际的点云获取过程中，由于点云的获取会出现孔洞、旋转错位、平移错位等，因此要得到完整的重建表面就需要对初始点云进行配准，以得到被测物体的完整三维模型。点云配准算法按照实现过程可以分为粗匹配和精确配准，确定一个刚体变换，将从各个视角得到的点集转换到一个统一的坐标系下形成完整的数据点云，最后进行可视化操作。配准的最终目的是求得坐标变换参数R(旋转矩阵)和T(平移矩阵)，使得不同视角下获得的三维数据经坐标变换后的距离最小。

2.1 点云粗匹配的步骤

点云粗匹配是指在点云之间初始转换矩阵位置是，通过提取各自点云里的特征点并获取其位置处的特征描述符来唯一性的代表各自点云，继而正确的匹配两点云的特征描述符，求取平移向量和旋转矩阵，经过转换将散乱点云初始位置对齐，提高ICP算法精确匹配的匹配精度，图2所示为点云粗匹配流程图。

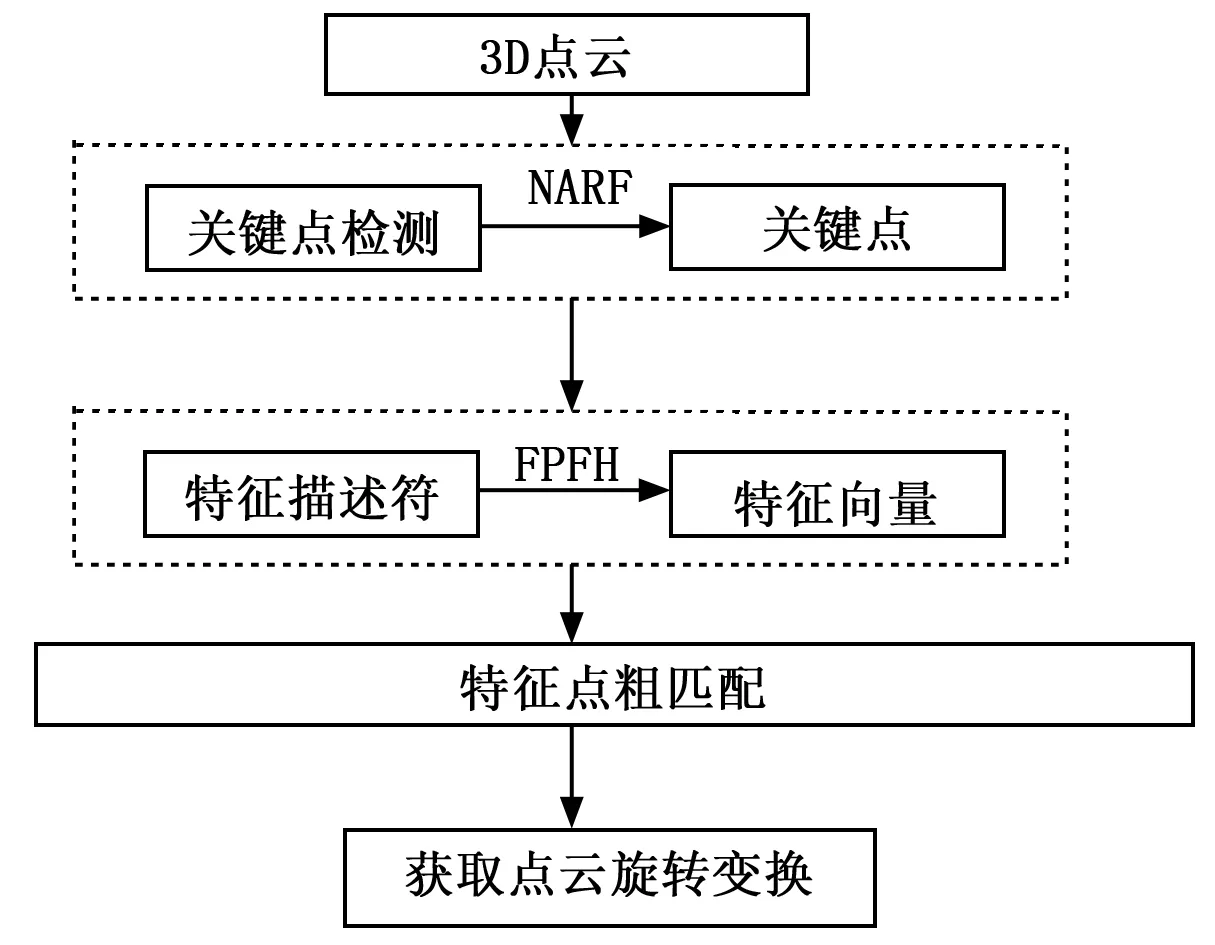
图2 点云粗匹配流程图

2.2 点特征直方图(PFH)

点特征直方图(PFH)是一种以统计直方图的形式来描述一个样本点周围的局部几何特征信息的点特征表示方法，PFH统计的是样本点与其k邻域之间的关系和它们估计的法线之间的关系，即通过估计法线方向之间所有的相互作用，试图得到最好的样本表面变化情况，以描述样本的几何特征。图3所示表示的是一个查询点(pq)的PFH计算的影响区域，半径为r，(pq)的所有k邻元素全部互相连接在一个网络中，最终PFH描述子通过计算邻域内所有两点之间关系而得到的直方图。

图3 查询点pq的PFH计算的影响区域

其具体计算如下：

1)对样本点p查询其邻k临域内所有邻近点。

2)对点p的k邻域中每对点ps和pt(s!=t)和它们对应的估计法线ns和nt，定义一个uvw坐标系来计算ps和pt以及它们对应的估计法线ns和nt之间的偏差，在其中的一个点上定义一个固定的局部坐标系，如图4。

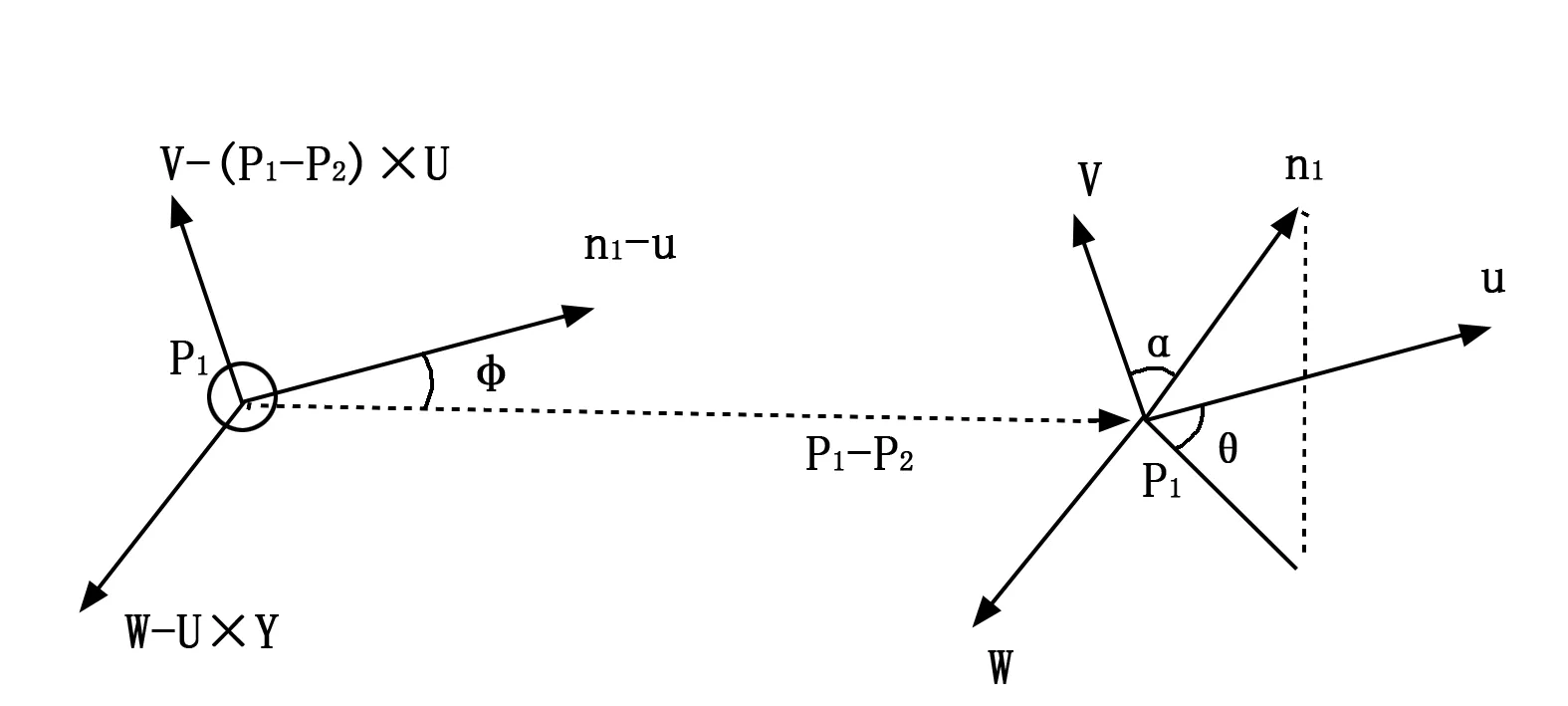
图4 一个固定的局部坐标系

(1)

使用上图的uvw坐标系，用下面一组角度来表示估计法线ns和nt之间的偏差：

(2)

(3)

(4)

‖pt-ps‖表示两点间的欧式距离，pq的所有k近邻点中任意两点之间的关系就可以用(α,β,θ,d)表示。邻域内所有的四组值以统计的方式放进直方图，就得到pq点的直方图特征。

2.3 快速点特征直方图(FPFH)

快速点特征直方图FPFH(fast point feature histograms)[10]是在PFH的基础上通过简化邻域间的互联降低了直方图的特征计算复杂度，使其复杂度由O(nk2)降低为O(nk)，FPFH对每一个样本点，首先计算这个点和它的k邻域内每个点之间α,β,θ3个特征值，统计输出成一个简化的点特征直方图SPFH(simple point feature histograms)，然后重新确定每个点的k邻域，利用公式(5)：

(5)

结合邻近点pk的SPFH值来计算pq最终的直方图FPFH。式中，权重ωk定义为查询点pq和 邻近点pk间的距离，表1是各个描述子维度对比。

表1 局部特征描述符比较

从表1中可以看出相比于其它3个描述符，FPFH的维度最小，大大降低了其时间复杂度，提高了运算速度。

3 ICP点云精确匹配算法

ICP算法的核心思想是：对不同坐标系下的两个点云，找到其对应点迭代的缩小匹配点间的距离，直到距离小于设定的阀值，最终得到点云集间的最优刚体变换，实现点云的配准，计算过程如下所示：

1)基于投影映射法的匹配点对获取，由于摄像机一直处于运动状态，所以必须将摄像机不同位置下获得的点云数据由摄像机坐标转换为全局坐标，进行融合。ICP算法利用基于投影映射法获取匹配点对，首先计算每帧摄像机坐标Ok到全局坐标Og的刚体变换矩阵，用Tk,g=[Rk,g/tk,g]表示变换矩阵，Rk,g表示旋转矩阵，tk,g表示平移向量。对于点云空间集Vk中任意一点S，坐标向量为Vk(u,v)，按照(5)式将摄像机坐标系下的任意定点坐标向量Vk,g(u,v)及法向量Nk,g(u,v)，转换到全局坐标系Og下，利用(6)式前一帧变换逆矩阵，将Og下任意点向量Vk,g(u,v)映射到Ok-1坐标系下，然后通过摄像机反透视投影获得对应点坐标(u',v')。

(5)

(6)

2)点到切平面距离误差函数估计配准参数，距离误差函数的优化，本文采用文献[14]提出的方法，将当前帧点云中的点到其在前一帧点云中的对应点所在切平面的距离作为误差函数，误差函数如(7)式：

(7)

(8)

(9)

其中，

4)重复迭代：当两次迭代更新矩阵满足一定的阀值，则停止迭代，转换矩阵等于最后一次迭代矩阵。

4 仿真结果及分析

仿真实验在VisualStdio2010环境下Inter(R)—core(TM)i3-4050 3.5GHz，4GB内存的PC机上结合PCL点云开源库[15]运行，为了验证本文方法的有效性，实验数据采用待配准的两只斯坦福兔子点云分别作为源点云和目标点云。

4.1 特征点估计

表面法线是几何体表面的重要属性，由于我们获取的点云数据集在真实物体的表面表现为一组顶点样本，因此我们直接从点与数据集中近似推断表面法线。图5按每10个点显示法线方向，由图中可以看出点云表面法线方向一致。

图5 点云法线估计

4.2 点特征直方图

表面法线和曲率估计是某个点几何特征的基本表示法，虽然计算快速容易，但获取的信息有限，通过有限的参数值来近似表示一个点的K邻域的几何特征。然而大部分场景中包含许多特征点，这些特征点有非常相近的特征值，因此采用点特征直方图，减少全局的特征信息。下图分别是bun0和bun4两个三维点云及其对应点的FPFH点特征直方图，通过点特征直方图获得特征描述子，获得匹配点对。

图6(a)(b) 分别表示每幅图对应的关键点处的FPFH点特征直方图，可以看出使用局部特征的直方图形式表示后，特征之间的差异量化的更加明显。

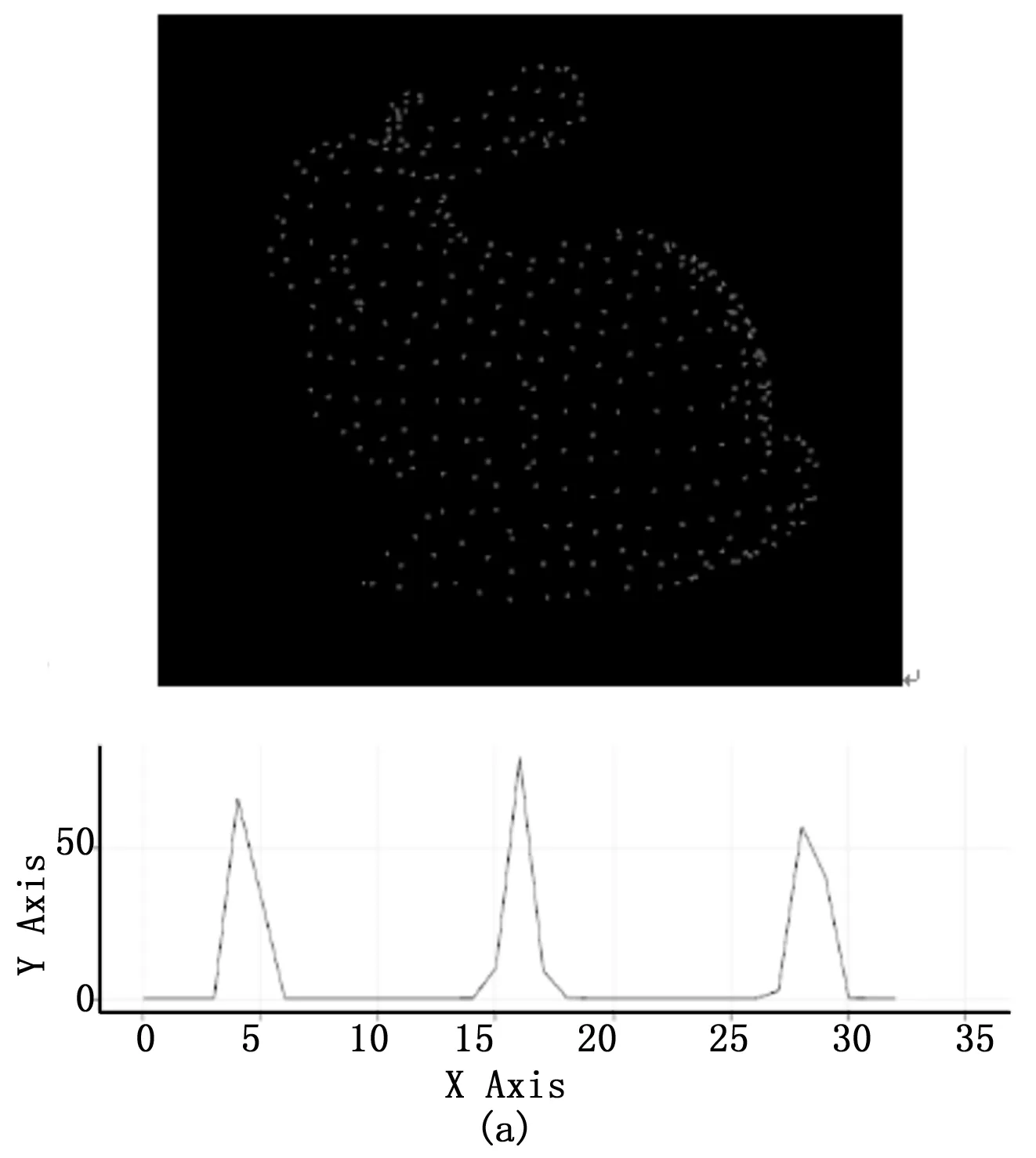
图6 两幅点云各自关键点处的FPFH

4.3 对应点估计

通过两侧扫描的点云数据获得的两组特征向量，在此基础上，找到相似特征获得数据的特征点对，在此基础上对点云进行配准,如图7所示。

图7 对应点估计

图8～图10 分别展示了点云未配准之前，直接使用ICP算法和使用改进型算法所得效果。可以看出，未配准之前，点云散乱的堆积在一起; 直接使用ICP配准，虽有一定效果，但误差非常大; 而使用改进型算法配准后的点云完美的结合到一起。

图8 点云未配准前

图9 直接使用ICP算法进行精确配准

图10 本文方法

本文采用基于FPFH特征点对的点云粗匹配，采用SAC-IA算法执行配准计算，在该算法中有一个最关键的参数，即Maxcorrespondencediatance，为两个点云中对应点对之间的最大距离，图11是对应点最大距离与拟合系数的对应关系图:

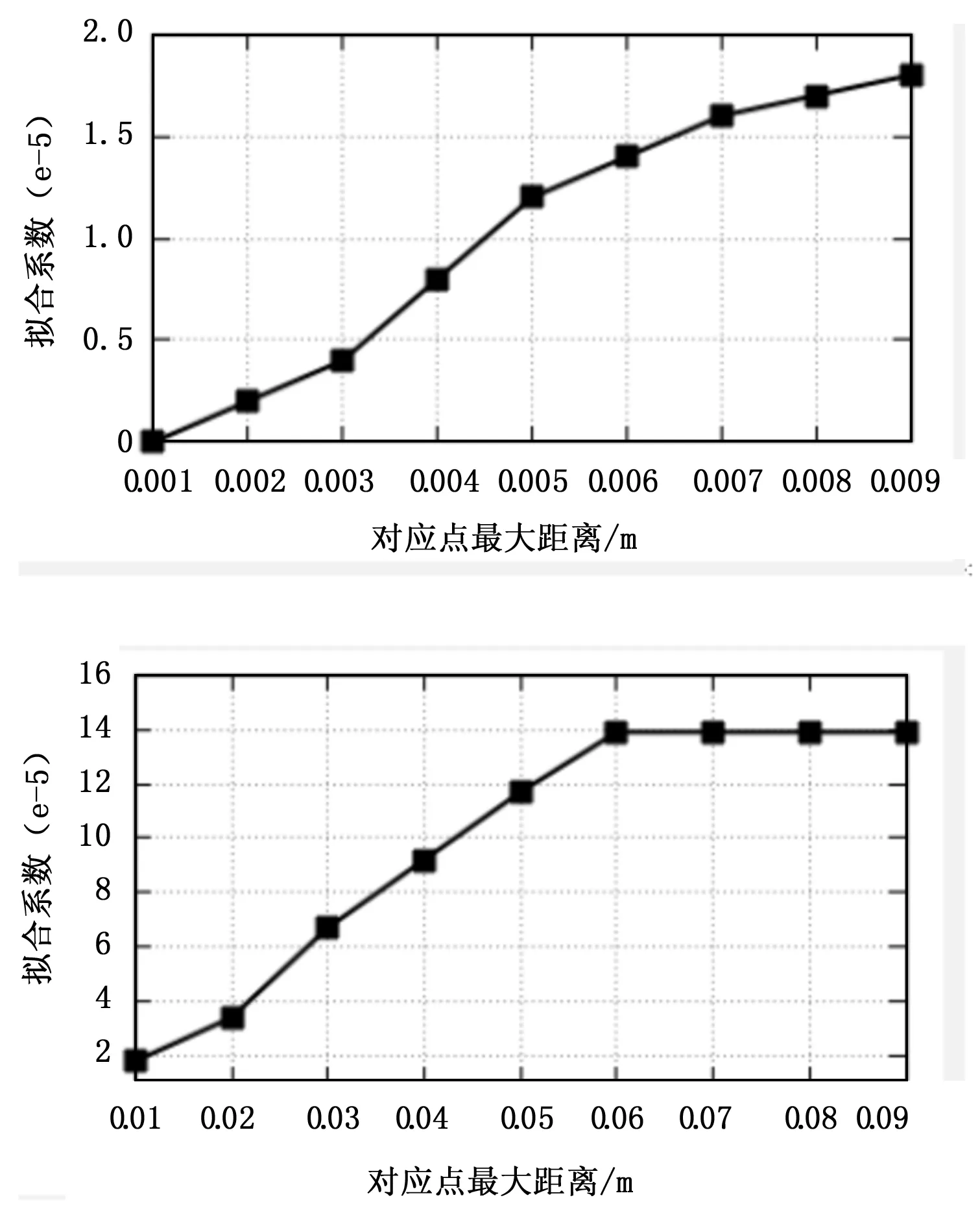
图11 对应点对与拟合系数函数关系

从图中可以发现，随着对应点距离的增大，对应的拟合系数也在逐渐增大,当增加到一定程度，趋于一个定值。但是对应点对最大距离的减小又会直接增加时间复杂度，当拟合系数为0.000 02时就可达到良好的匹配效果，因此综合计算复杂度与匹配精度，与之对应的该参数值为0.01，得到粗匹配结果，然后对其结果进行ICP精确匹配，最终匹配精度为0.000 025，与未进行点云粗匹配的匹配精度0.000 063相比，提高了百分之60.3%，此时的转移矩阵和平移向量分别为:

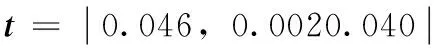
为了进一步验证本文算法的有效性，对ICP算法和本文改进的算法精度进行比较，如表2所示，相比于经典ICP算法，本文克服了其初始点云不收敛从而引起较大匹配误差的缺点，大大提高了匹配精度。与现有的其它两种匹配算法相比本文算法得到的匹配误差最小。

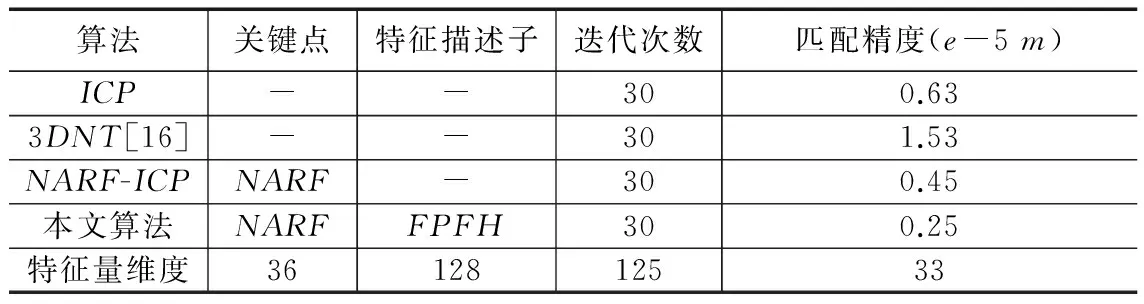
表2 同类方法配准精度比较

综上实验结果，在大量的实验基础上，利用FPFH特征描述符对原始散乱点云进行粗匹配的基础上，再进行ICP精确匹配，图像匹配精度提高，很好的实现了点云配准。

最后对配准后的点云进行三角化得到最终的重建模型，如图12所示。

图12 三维模型

5 小结

针对点云处理流程中，因ICP算法需要收敛的初始位置，文中使用基于FPFH描述子的点云粗匹配，提高匹配精度，取得了良好的拼接效果，从而实现了三维重建。实验结果证明本文的方法可以有效地实现三维重建，具有一定的实际应用价值。

[1]ArafaMajdi,MohamedChafikBakkayandEzzeddineZagrouba.3DModelingofIndoorEnvironmentsUsingkinectsensor[A].2013IEEESecondInternationalConferenceonImageInformationProcessing(ICIIP)[C].Shimla,IEEE, 2013, 67-72.

[2] 艾 达,乔明明.三维激光扫描技术在犯罪现场重建中的应用[D].西安：西安邮电大学学报,2013.

[3]BeslPJ,McKayHD.AMethodforRegistrationof3DShape[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1992. 14(2): 239-256.

[4] 王 君.基于kinect的三维场景重建研究[D].长沙：中南大学，2013.

[5]RichardANewcombe,ShahramIzadi,OtmarHilliges,DavidMolyneaux,DavidKim.KinectFusion:Real-TimeDenseSurfaceMappingandTracking[A].2011 10thIEEEInternationalSymposiumonMixedandAugmentedReality(ISMAR)[C].Basel.2011,127-136.

[6]NguyenCV,IzadiS,LovellD.ModelingKinectsensornoiseforImproved3DReconstructionandTracking[A].Proceedingsofthe2012SecondInternationalConferenceon3DImaging,Modeling,Processing,Visualization&Transmission,2012[C].IEEEComputerSociety.

[7]WanY,WangJ,HuJW.AStudyin3D-ReconstructionUsing

KinectSensor3D-Reconstruction[A].2012 8thInternationalConferenceonWirelessCommunications,NetworkingandMobileComputing(WiCOM)[C].Shanghai,China.2012,1-7.

[8] 叶日藏.基于Kinect深度传感器的三维重建技术应用研究[D].广东:华南理工大学，2013.

[9] 何文峰. 大型场景三维重建中的深度图像配准[D].北京：北京大学,2004.

[10]RaduBogdanRusu,NicoBlodow,MichaelBeetz.FastPointFeatureHistograms(FPFH)for3DRegistration[A].2009IEEEInternationalConferenceonRoboticsandAutomation[C].Japan.2009,3212-3217.

[11]高珊珊.基于三维激光扫描仪的点云配准[D].南京：南京理工大学，2008.

[12] 张旭东,吴国松等.基于TOF三维相机相邻散乱点云配准技术研究[J].机械工程学报，2013,49(12):8-22.

[13]陈聪梅.基于Kinect的三维点云数据处理[D].苏州：苏州大学,2013.

[14]SzymonRusinkiewiczMarcLevoy.EfficientVariantsoftheICPAlgorithm[A].Proceedings.ThirdInternationalConferenceon3-DDigitalImagingandModeling[C]. 2001:145-152.

[15]RaduBogdanRusuandSteveCousinsWillowGarage. 3Dishere:PointCloudLibrary(PCL)[A].InternationalConferenceonRoboticsandAutomation(ICRA)[C]. 2011IEEE.Shanghai:2011,1-4.

[16]胡修祥,张 良.结合NARF特征的改进型3D-NDT多视野点云配准[J].信号处理,2015,31(12):1674-1679.

Research and Realization of 3D Restruction Based on FPFH

Ai Da1，Wang Miao1，Ni Guobin2

(1.Xi’an University of Posts and Telecommunications, Key Laboratory of electronic information application technology of Site-survey of Ministry of public security, Xi’an 710061,China)2.School of Electronic Engineering,Xi’an University of Posts and Telecommunications, Xi’an 710061, China)

The article describes a different perspective on the basis of three-dimensional point cloud pairwise data registration,for accurate matching algorithms ICP need to make an initial point cloud convergence, otherwise unable to obtain accurate matching results, this artice proposes a feature based on FPFH Descriptors coarse matching feature method.Adjust the initial position of two point clouds for ICP algorithm provides a good initial position to further improve the matching precision point cloud. And on this basis to get through a lot of experiments as a function of the largest point distance and the best fitness score between correspondence pairs to obtain the optimal value match, it is proved that coarse matching can make the best fitness score up to 60.3%.

registration;FPFH descriptors;coarse matching

2016-01-12；

2016-03-07。

公安部重点实验室项目(2014GABJC02)。

艾 达(1975-)，男，博士，高工，硕导，主要从事数字图像处理方向的研究。

1671-4598(2016)07-0232-05

10.16526/j.cnki.11-4762/tp.2016.07.063

TP391 文献标识码：A