一种改进的空间信号完好性监测算法

汪冬瑾，张 英，刘建敬，李晓东

(1.宇航智能控制技术国家级重点实验室，北京 100854； 2.北京航天自动控制研究所，北京 100854)

一种改进的空间信号完好性监测算法

汪冬瑾1,2，张 英1,2，刘建敬1,2，李晓东1,2

(1.宇航智能控制技术国家级重点实验室，北京 100854； 2.北京航天自动控制研究所，北京 100854)

针对Galileo系统空间信号完好性监测方案中两项关键技术点做出改进，首先提出改进临界圆法，从坐标系转换角度解决最坏用户位置方位角转换的复杂度问题；其次引入“截尾概率包络”概念，改善原模型对非零均值空间信号误差值高斯分布的过分包络问题；最后在无故障、阶跃类故障、斜坡类故障3种模式下，对比分析改进方案前后系统的完好性性能；结果表明，完好性阈值对实时空间信号误差估计值的平均包络紧度由3.89米改善至2.62米，对斜坡类故障的告警更加及时。

空间信号完好性；改进临界圆法；截尾概率包络；阈值包络紧度；告警性能

0 引言

为了满足用户的高可靠性服务需求，导航系统建立之初，国际民航组织就提出精度、完好性、连续性、可用性等四方面要求。其中，完好性是指导航系统不能用于导航时及时、有效地向用户提供告警信息的能力[1]。空间信号完好性监测则是GNSS导航系统完好性监测体系重要组成之一。目前，存在两种空间信号完好性监测方案：1)新一代GPS系统的用户距离精度完好性监测方案[2]；2)Galileo系统提出的空间信号精度(SISA, signal-in-space accuracy)/ 空间信号监测精度(SISMA，signal-in-space monitoring accuracy)完好性监测方案[3-4]。但两种空间信号完好性监测方案仍未投入应用，同时我国北斗导航系统的完好性监测体系短缺。

本文在系统地分析Galileo系统空间信号完好性监测方案的基础上，对关键技术点——最坏用户位置(WUL, worst user location)解算和空间信号误差(SISE, signal in space error)包络模型的不足之处提出改进方案，并仿真分析改进方案在无故障、阶跃类故障、斜坡类故障3种模式下，对系统完好性性能的改善。

1 Galileo完好性监测方案

1.1 方案原理

Galileo空间信号完好性监测方案的监测对象选取为空间段误差在用户伪距域的投影值，即SISE。完好性监测参数包括SISA和SISMA/完好性标识(IF, integrity flag)[3]。系统工作流程如图1所示。

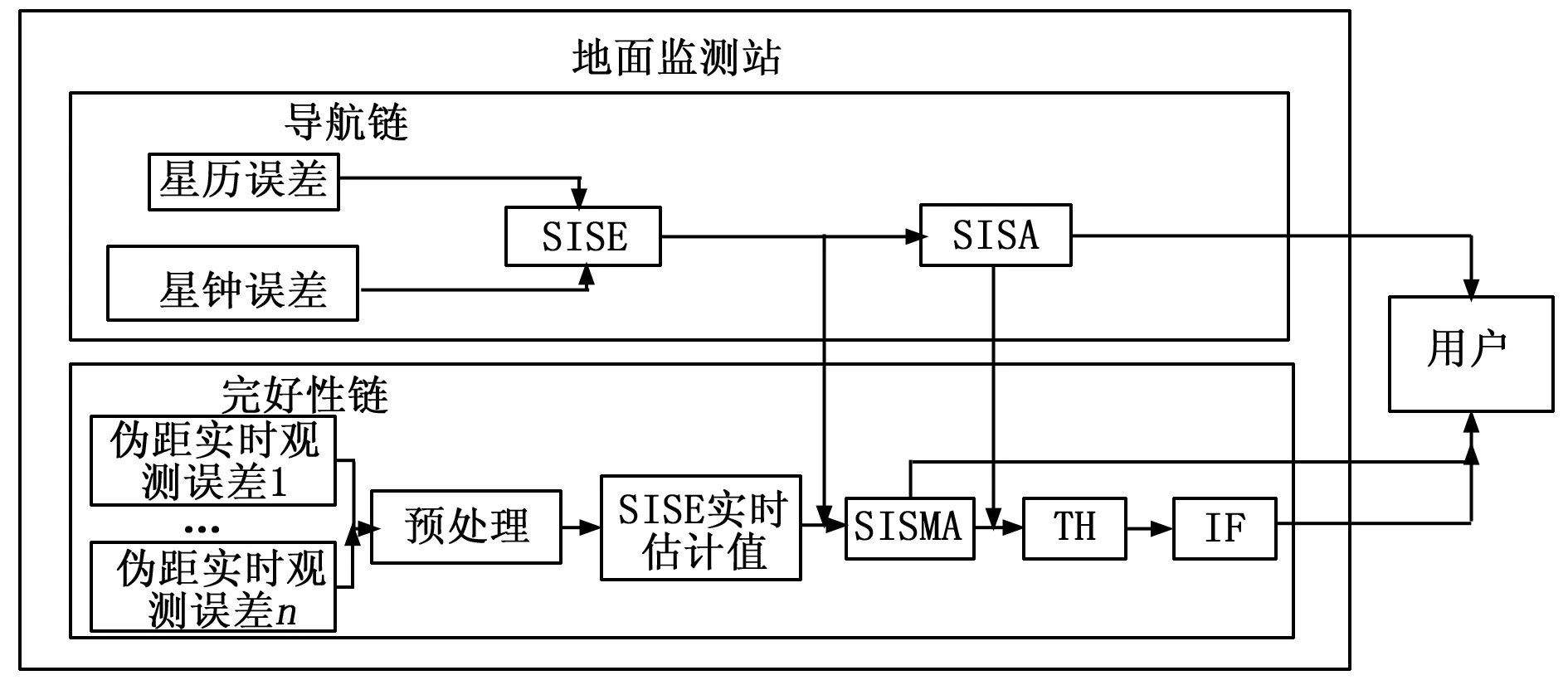
图1 系统完好性监测流程

SISA为更新周期内、一定置信水平下卫星可视域内最大SISE的统计分布，用于衡量SISE广播值的精度，更新周期为100分钟。SISMA为一定置信水平下卫星可视域内最大SISE估计差值的统计分布，用于监测SISA的预报质量，更新周期为30 s。IF由SISA、SISMA联合生成，更新周期为1 s[4]。用户段根据这3种完好性参数计算定位保护水平，以确定定位结果的可靠性。

1.2 模型分析

由上述定义可知，SISA/SISMA算法包含两个核心模块：卫星可视域内最大误差值确立和一定置信水平下的误差统计分布。

1.2.1 临界圆法

最大误差值确立即为求解具有最大误差投影值的用户位置——最差用户位置。临界圆法利用卫星、地心和轨道误差矢量构成的二维平面中，星下点F与误差矢量投影点A的方位角与WUL几何关系进行解算[5-9]，角度几何关系及解算流程如图2所示。

该算法模型存在两个问题：1)由于球模型的方位角推导公式的不准确性，A、F、WUL可能不在一个平面上，导致WUL出现误差，需要迭代修正；2)球模型转换至椭球模型过程中，需要分四种情况分别迭代计算，方位角几何关系转换复杂度高，迭代周期长。

图2 与WUL相关的角度

1.2.2 误差统计分布

SISE广播值包络模型基于误差为无偏高斯分布的前提条件，SISA取值为SISA=k·σΔRWUL。但实际SISE广播值存在0至1米的均值[10]。以99.9%的界定概率为例，原模型计算得到的SISA值将SISE广播值的均值和方差同时放大3.29倍，过分夸大了SISE的真实情况，容易引发虚警，影响系统可用性。

2 改进方案

2.1 改进临界圆法

WUL的确定是完好性参数SISA、SISMA算法的核心模块之一，其准确性和算法复杂度对提高完好性参数求解的可靠性和实时性具有非常重要的意义。

文中改变原临界圆法从纯方位角几何关系推导的思路，采用坐标系转换模块将地心地固坐标系转换至OAF确定的平面确定的新坐标系，利用A、F、WUL的坐标关系求解，解决了原算法中三点不在一个平面的问题，降低算法复杂性。

2.1.1 算法模型

(1)球模型中WUL解算：

图3 新坐标系及角度关系示意图

则球模型中，ECEF坐标系下的最坏用户位置可由下式求得：

(1)

(2)

(3)

(4)

其中，xWUL、yWUL、zWUL为ECEF坐标系下，最坏用户位置。rWUL为ECEF坐标系下最坏用户位置至球心的距离。

(2)椭球模型中WUL解算

WUL值在球模型至椭球模型的转换关系如图4所示。

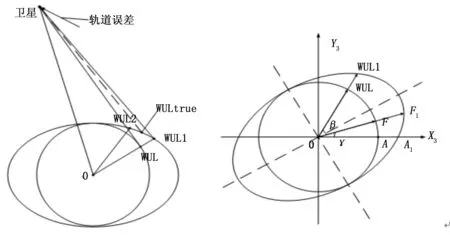
图4 球体与椭球体的WUL示意图

图中点O为地心，WUL为上述球模型解算得到的最坏用户位置，与卫星的连线交椭球面于点WUL2，连接地心延长线则交椭球面于WUL1点。椭球面上某点E的高度截止角，即E点至卫星的方向矢量与过该点的椭球切平面的法线矢量NE的夹角φE，可表示为：

(5)

显然φWUL2>φWUL>φWUL1。椭球模型中的WUL在WUL1和WUL2之间，称为WULtrue。按照一定的步长修正中心角β，向WUL2点方向逼近，返回球模型，直到满足φWUL1≥φWUL，即可求得WULture。

2.1.2 仿真验证

从图2中WUL相关角度的严格几何意义出发，WUL真值应同时满足下式：

(5)

以GPS系统的PRN6号卫星2014年3月23日的星历为例，历元间隔30秒，临界圆法和改进临界圆法WUL真值误差和解算时间的均值仿真结果如下表1所示。

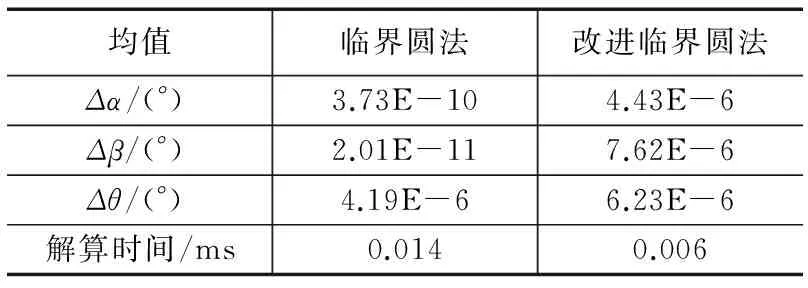
表1 WUL结果及解算时间统计

由上表可知，改进临界圆法解算的WUL准确性更高，真值误差量级由10-6提升至10-10；解算时间比原临界圆法低一个量级。从仿真结果还可以得出一条结论，地心至卫星的方向矢量与卫星轨道误差矢量的夹角绝大多数情况下大于最小截止角θ0相应的天顶角α0，即WUL绝大多数情况下在危险圆上。

2.2 截尾概率包络模型

包络模型的有效性直接决定完好性参数SISA对SISE广播值的衡量精度。若过小包络，则完好性风险增大，影响系统的可靠性；若过分包络，容易引发虚警，降低系统可用性。文中引入“截尾概率包络”概念解决由SISE非零均值特性，引入的过分包络问题。

2.2.1 算法模型

“截尾概率包络”的概念：高斯分布N(0,SISA2)在1σ门限外的高斯截尾概率大于完好性风险指标对应的界定概率下，门限外，SISE非零均值高斯分布的高斯截尾概率。其中，高斯截尾概率是指高斯分布位于门限外的累积概率，以标准差为σ的零均值高斯分布为例，可表示为：

(6)

其中，[x1,x2]为门限；F(x2)-F(x1)为取值范围内的累积分布概率。

假定SISE投影值的均值为μ，均方差为σ，界定概率为px1,x2，则：

(7)

其中，x1=-k·σ+μ，x2=k·σ+μ，k为概率px1,x2对应的分位数。

首先假定μ>0，由高斯分布特性可知，当x3=-(k·σ+μ)

2.2.2 仿真验证

以GPS系统的PRN8号卫星2014年3月23日0时起为时4 h的实际星历数据为例，历元间隔30秒，置信概率取为99.9%时，则最大SISE投影值与算法改进前后SISA值的仿真结果如图5所示。由图可得出如下结论：1)SISA值能够大致体现当前历元，卫星可视域内最大SISE伪距域投影值的变化趋势；2)原SISA值过分包络SISE，基于非零均值SISE的算法模型对包络差值改进效果最大达3.02米。

图5 两种算法模型的SISA值比较

3 系统性能分析

3.1 仿真数据配置

仿真环境：①卫星类型及数目：24颗MEO卫星；②地面监测网络：Galileo系统拟布设于全球的30个监测站；③监测站高度截止角：15°；④仿真时长6 000秒，仿真时间间隔1秒；⑤完好性参数SISA、SISMA的置信概率：99.9%。

3.2 系统性能仿真结果

选取系统的完好性告警能力作为性能衡量指标，即完好性阈值(TH, integrity threshold)对实时空间信号误差的包络能力。首先分析系统无故障模式，限于篇幅，仅以2颗卫星为例，其他未显示卫星也有同样规律。卫星的可视监测站数目与算法改进前后的实时SISE和完好性阈值TH的仿真结果如图6所示。

由图6可知，无故障模式下，TH精度随卫星可视监测站数目的减少而下降；算法改进前后都能够对实时SISE完全包络；为衡量包络紧度，统计TH与实时SISE在仿真时长内的差值平均值。结果表明，算法改进前后，平均包络紧度由3.89米改善至2.62米。

为有效检验系统的故障告警性能，引入两类常见故障——阶跃类故障(星钟跳变)、斜坡类故障(星钟漂移)。两种故障

图6 无故障模式下系统告警性能对比

模式下，算法改进前后的实时SISE与完好性阈值TH的仿真结果如图7、图8所示。其中，两类故障的仿真时长均为1 201秒至3 000秒。

图7 阶跃类故障模式下系统告警性能对比

图8 斜坡类故障模式下系统告警性能对比

由上图7和图8可看出，实时SISE估计值随故障误差累积而增大，仅当故障误差达到某一门限值，实时SISE估计值超过阈值，完好性标志IF置“1”，系统告警。由于阶跃类故障的实时SISE值变化为瞬时值，远短于1s，两种算法均能及时告警。而对于斜坡类故障，实时SISE值不断增大，当SISE值超过TH值则系统告警。因此改进后算法能够更加及时告警。

4 结束语

文中系统地分析空间信号完好性监测系统的监测机理和算法模型，针对其中两个关键技术点的不足之处，提出优化方案：改进临界圆法估计最坏用户位置WUL；基于非零均值SISE的SISA算法优化原算法过分包络问题。最后仿真分析无故障、阶跃类故障、斜坡类故障三种模式下，算法改进前后系统的完好性告警性能。结果表明，改进后的算法在保证TH对实时SISE的包络能力条件下，将包络紧度由3.89米改善至2.62米；且告警更加及时。

[1]GroverBrownR.GlobalPositioningSystemTheoryandApplication[M].AmericanInstituteofAeronauticsandAstronautics,1996,143-164.

[2]GPSInterfaceSpecificationIS-GPS-200F[EB/OL].http://www.navcen.uscg.gov.

[3]VeitOehler.TheGalileoIntegrityConcept[A].Proceedingsofthe17thInternationalTechnicalMeetingoftheSatelliteDivisionoftheInstituteofNavigation(IONGNSS2004)[C]. 2004; 604-615.

[4]HelmutBlomenhofer,WalterEhret.PerformanceAnalysisofGNSSGlobalandRegionalIntegrityConcepts[A].Proceedingsofthe16thInternationalTechnicalMeetingoftheSatelliteDivisionoftheInstituteofNavigation(IONGNSS2003)[C]. 2003; 991-1001.

[5]ShaojunFeng,Washington.AnEfficientWorstUserLocationAlgorithmfortheGenerationoftheGalileoIntegrityFlag[J].JournalofNavigation, 2006,59(03): 381-394.

[6] 谷守周，秘金钟.Galileo完备性系统中WUL算法研究[J]. 测绘科学，2011,36(2):17-19.

[7] 秘金钟.GNSS完备性监测方法、技术与应用[D]. 武汉：武汉大学，2010.

[8] 张雪辉，贝 超，王 芳. 最差用户位置算法研究与仿真分析[J]. 航天控制，2010,28(2): 29-35.

[9]FanMJ,ZhouJH.AlgorithmofAnalysisfortheImprovedIntegrityIndexSISMAofGALILEOSystem[A].ChinaSatelliteNavigationConference(CSNC) 2012Proceedings[C]. 2012; 57-65.

[10]HengL,GaoGX,WalterT,etal.StatisticalCharacterizationofGPSSignal-in-SpaceErrors[A].Proceedingsofthe2011InternationalTechnicalMeetingoftheInstituteofNavigation[C]. 2011; 312-319.

An Improved Signal-in-Space Integrity Monitoring Algorithm

Wang Dongjin1,2, Zhang Ying1,2, Liu Jianjing1,2, Li Xiaodong1,2

(1.State Key Laboratory of Aerospace Intelligent Control Technology, Beijing 100854, China;2.Beijing Aerospace Automatic Control Institute, Beijing 100854, China)

To improve the algorithm of two key technologies in the Galileo signal-in-space integrity monitoring system, an improved critical circle method and a censored probability envelope model were proposed for the determination of the worst user location and enveloping the Signal-in-Space Error respectively. The improved critical circle method could obtain accuracy WUL directly by coordinate conversion to simplify purely geometric derivation. The censored probability envelope model solved the over-bound problem by using a new envelop concept for the SISE distribution with non-zero mean. Finally, simulations were conducted to compare the integrity performance of the improved algorithm with the original one in fault-free, step failure and slope failure modes. The results show that the integrity threshold envelope tightness improves from 3.89 meters to 2.62 meters and system alarm more timely than the original algorithm in the slope failure mode.

signal-in-space integrity; improved critical circle method; censored probability envelope model; integrity alarm performance analysis; envelope tightness

2016-01-11；

2016-03-07。

国家重点基础研究发展计划(973)项目(2010CB731805)。

汪冬瑾(1991-)，女，安徽滁州人，硕士，主要从事卫星导航算法设计方向的研究。

1671-4598(2016)07-0062-03

10.16526/j.cnki.11-4762/tp.2016.07.017

TP3 文献标识码：A