样本不平衡的睡眠数据分期研究

李玉平, 夏　斌

(上海海事大学 信息工程学院，上海 201306)



样本不平衡的睡眠数据分期研究

李玉平, 夏斌

(上海海事大学 信息工程学院，上海 201306)

睡眠数据中各个阶段的样本数差异较大，睡眠数据的自动分期是一个典型的样本不平衡的机器学习问题。均衡样本方法通过抽样的手段来平衡样本，是解决样本不平衡问题的主要方法。采用均衡样本方法来平衡睡眠数据的不同阶段的样本，并且结合多域特征(时域、频域、时频域以及非线性)和随机森林分类算法进行分类预测。比较分析了样本均衡处理和非均衡处理的分类结果，发现均衡处理后的数据取得了更好的分类效果。

睡眠分期；数据不平衡；随机森林

引用格式：李玉平, 夏斌. 样本不平衡的睡眠数据分期研究[J].微型机与应用，2016,35(18)：55-57,61.

0　引言

睡眠是生命过程中必不可少且十分重要的生理现象。依据国际R&K标准[1]，睡眠期可分为快速眼动期、非快速眼动期(S1，S2，S3，S4)以及清醒期，区别分期主要以眼球是否进行了阵发性快速运动为标准。根据上述睡眠分期标准，睡眠数据可分为6类，且不同类别的数据量之间具有较大的差异性，即睡眠数据分期存在样本不平衡的问题。在应用机器学习研究睡眠分期过程中，样本不平衡会导致睡眠分期结果不准确，睡眠分期的可信度降低。在以前的睡眠分期研究中，研究的主要是睡眠数据特征的提取以及分类算法的选取[2-4]，并没有研究睡眠分期样本不平衡问题。本文采用EEG、EOG、EMG 3种信号5个通道的睡眠数据，研究中发现，EOG信号会出现在EEG信号的一些睡眠分期(如清醒状态和快速眼动状态)中，这种数据会对睡眠分期产生不好的影响[5]。本文通过对睡眠分期样本不平衡的研究以及信号混杂的处理，进一步提高睡眠分期的准确度，同时对相关睡眠疾病的诊断和治疗提供重要的参考意义。

基于以上睡眠数据分期的讨论，本文采用均衡采样的方法解决睡眠分期样本不平衡问题，同时研究睡眠数据的特征提取以减少信号混杂对睡眠分期的影响。

1　方法

1.1特征提取

睡眠数据的特征主要划分为时域特征、频域特征、时频域特征以及非线性特征。本文中，提取EEG、EOG和EMG每种信号各38种特征。

特征参数如下：第1～6种是6个时域特征[6-8]：均值(Mean)、方差(Variance)、峰度(Kurtosis)、偏度(Skewness)、过零率(Number of zero crossing，NZC)、最大值(MaxV);第7～19种是频域特征[8-10]：对4个子节律波分别提取各自范围的功率谱能量(SP_),计算0.01～30 Hz频带的总功率谱能量(SP_D)，以及总功率谱能量的规范化能量比(NSP_)，即theta/beta、beta/alpha、(theta+alpha)/beta, (theta+alpha)/(beta+alpha)；第20～35种是时频域特征[8-10]：4个子节律波在当前频带范围上小波系数的均值、能量、标准差以及相对于总频带范围的绝对平均值；第36～38种特征分别是Petrosian分形指数、Hurst指数、排列熵[11-12]。

1.2均衡采样

睡眠数据存在样本不平衡的问题，在6类的数据中，最多一类的数据集与最少的一类数据集的比例达到10倍以上，存在严重不平衡现象。本文应用均衡采样的方法处理样本失衡的问题[13]:(1)分别计算6类睡眠分期数据的个数n1、n2、n3、n4、n5、n6；(2)去掉个数最少和个数最多的个数值，剩余为n1、n2、n3、n4，计算这4类个数的平均值n；(3)对6类数据按个数平均值n采样，不足平均个数的类别重复采样，超过平均个数的类别欠采样；(4)整合6类数据采样得到的新数据集即为均衡处理后的数据[4，14]。

1.3随机森林分类器

随机森林模型是决策树集成的算法，并且由一随机向量决定决策树的构造。通过训练集得到随机森林模型后，当有一个新的输入样本进入时，就让随机森林的每一棵决策树分别进行判断，判断样本所属类别，然后计算哪一个类别被选择最多，就预测该样本所属的类别。随机森林算法特征参数较多，测试结果不会出现过拟合的情形；能够处理高维度特征的睡眠数据，不用做特征选择，对数据集的适应能力强；训练速度快，能够检测不同特征之间的影响[13,15]。

随机森林实现过程为：(1)原始训练集为N，采用集成算法有放回地随机选取k个样本集构建k棵分类树，每次没有被抽到的样本组成k个袋外数据；(2)设定mall变量，在每棵树的每个节点处随机抽取mtry个变量(mtry,n,mall),然后在mtry中选择一个最佳的分类变量，变量分类的阈值通过检查每一个分类点确定；(3)每一棵树最大限度地生长，不做任何修剪；(4)将构造的多棵分类树组成随机森林，用随机森林分类器对新的数据进行判别与分类，分类的结果按树分类器投票数确定。

2　实验与结果

2.1数据

本文采用9名受试者的睡眠数据来验证分类方法和数据不平衡处理的可行性。数据集记录了这9名志愿者一晚上的睡眠数据，以1～9命名这些数据集。数据包含15个通道的睡眠时的信号数据以及呼吸频率和身体温度。对应的EEG、EOG、EMG信号按100 Hz进行采样。数据集处理部分，分别进行了7/3分和留一方法，采用这两种方法验证睡眠分期样本不平衡的处理效果。

2.2数据预处理

首先采用巴特沃夫滤波器提取原始睡眠数据中0.01～35 Hz的数据，并应用高斯归一化方法对数据进行归一化处理。由于采样的睡眠数据可能存在标签不正确的问题，因此会剔除不正确的标签数据。具体方法是，首先找出空标签或标签异常(不在已有类别中的标签)，根据标签对应的位置，剔除这些标签对应的数据集，最后更新数据集。采用以上方法进行数据预处理之后，得到7 461条数据。

2.3均衡采样数据

经预处理和特征提取之后，对9个受试者的数据进行整合，数据总量为59 680。采用7/3分数据集，即70%数据做训练集，30%数据做测试集，训练集数据量为41 773，测试集数据量为17 907。为了验证均衡采样的可行性，对训练集做均衡处理，得到22 465条新的训练集。

2.4结果

本文第一种验证方法是7/3数据集，结果如下：表1是所有数据集7/3分，对训练集进行均衡处理的分类结果准确率；表2是均衡采样数据集和普通数据集分类结果对比；表3是不同信号组合，均衡采样分类结果对比。

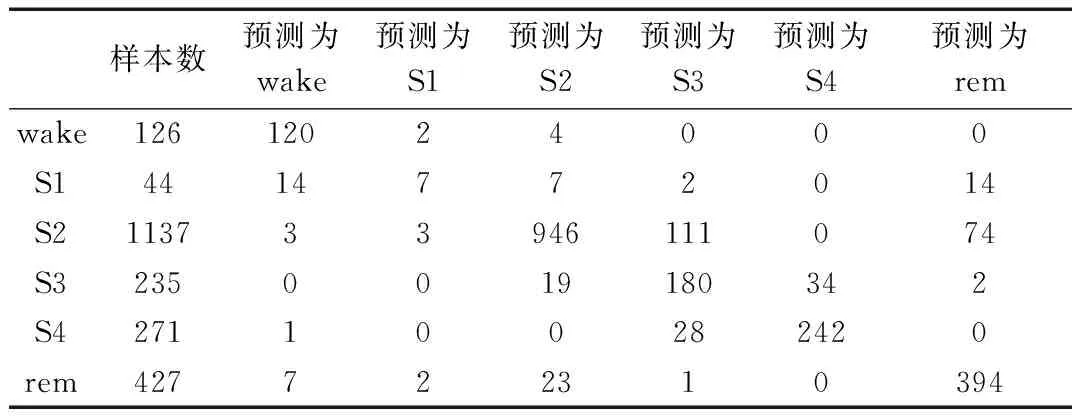
表1　均衡处理测试结果

表2　分类结果对比　(%)

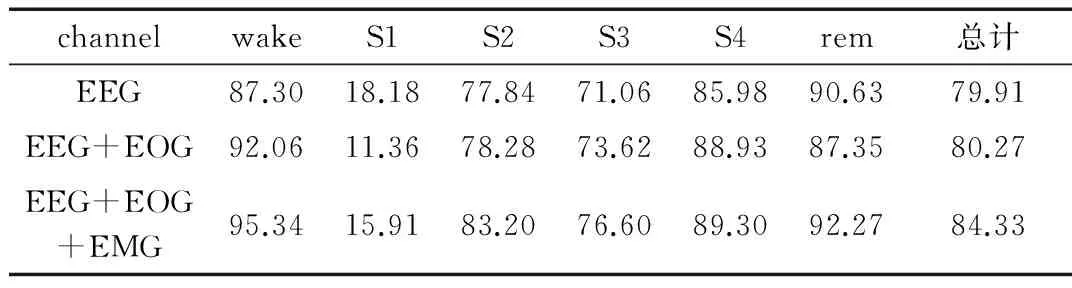
表3　不同信号组合分类结果对比　(%)

图1　均衡处理留一验证准确率

第二种验证方法是对9个受试者的数据集进行留一验证。分别提取其中8个受试者的数据集作为训练集做均衡处理，剩下1个受试者的数据集作为测试集。分类结果如图1所示。

由表1得知，同时考虑EEG、EOG、EMG 3种信号5个通道的数据集，得到的分类准确率达到84.33%，wake类别的分类准确率最高，模型对wake类别的泛化能力最好，而S1类别数据量最少，同时分类效果也最差。由表2得知：均衡处理之后，wake、S1、S3、rem这4类睡眠分期结果得到了提升，S4基本一致，S2的结果降低了。由表3知：提取一种信号EEG时，睡眠分期准确率比同时提取多种信号时的准确率低。由图1留一验证知，2、5、9号受试者睡眠分期的结果达到了80%以上,分类效果较好；3、6号受试者睡眠分期准确率较低。

3　结论

本研究采用了EEG、EOG、EMG 3种信号5个通道数据集，并且应用均衡采样的方法处理训练集数据不平衡问题，睡眠分期结果较好，平均分类准确率得到了提升，并且有4个睡眠分期的分类结果都得到了提升。在今后对睡眠分期样本不平衡的研究中，可以采用加权随机森林或其他的方法处理睡眠数据集不平衡的问题。

[1] RECHTSCHAFFEN A Q, KALES A A. A manual of standardized terminology, techniques, and scoring system for sleep stages of human subjects[J]. Psychiatry & Clinical Neurosciences, 1968,55.

[2] 李谷，范影乐，庞全.基于排列组合熵的脑电信号睡眠分期研究[J]．生物医学工程学志，2009，26(4)：869-872．

[3] Liu Derong，Pang Zhongyu，LLOYD S R．A neural network method for detection of obstructive sleep apnea and narcolepsy based on pupil size and EEG[J]．IEEE Transactions on Neural Networks，2008，19(2)：308-318．

[4] ANAND A, PUGALENTHI G, FOGEL G B, et al. An approach for classification of highly imbalanced data using weighting and undersampling[J]. Amino Acids, 2010,39(5):1385-1391.

[5] BREIMAN L, FRIEDMAN J, OLSHEN R, et al. Classification and regression trees[M]. New York: Chapman & Hall，1984.

[6] SMITH J R. Automated EEG analysis with microcomputers[J]. Medical Instrumentation, 1980,14(6):319-321.

[7] VURAL C, YILDIZ M. Determination of sleep stage separation ability of features extracted from EEG signals using principal component analysis[J]. Journal of Medical Systems,2010,34(1):83-89.[8]EN B, PEKER M, A ÇAVULU A, et al. A comparative study on classification of sleep stage based on EEG signals using feature selection and classification algorithms[J]. Journal of Medical Systems，2014，38(3)：1-21.

[9] HAMIDA T B， AHMED B. Computer based sleep staging： challenges for the future[C]. 2013 IEEE GCC Conference and Exhibition, 2013：280-285.

[10] AKIN M. Comparison of wavelet transform and FFT methods in the analysis of EEG signals[J]. Journal of Medical Systems,2002,26(3):241-247.

[11] FELL J, RSCHKE J, MANN K, et al. Discrimination of sleep stages: a comparison between spectral and nonlinear EEG measures[J]. Electroencephalography and Clinical Neurophysiology, 1996，98(5)：401-410.

[12] PEREDA E, GAMUNDI A, RIAL R, et al. Non-linear behavioor of human EEG: fractal exponent versus correlation dimension in awake and sleep stages[J]. Neuroscience Letters, 1998,250(2):91-94.

[13] 毛文涛，王金婉，等.面向贯序不均衡数据的混合采样极限学习机[J].计算机应用，2015, 35(8)：2221-2226.

[14] He Haibo,GARCIA E A. Learning from imbalanced data[J]，IEEE Transactions on Knowledge and Data Engineering，2009,21(9):1263-1284.

[15] BREIMAN L. Random forests[J]. Machine Learning，2001, 45(1):5-32.

Research on the stage of sleep data with imbalanced sample

Li Yuping, Xia Bin

(College of Information Engineering, Shanghai Maritime University, Shanghai 201306,China)

Sleep data in each stage is different, and the automatic staging of sleep data is a typical problem of sample imbalance.Balanced sampling method balances samples by sampling, and it is the main method to solve the problem of sample imbalance.In this paper, we use a balanced sample method to balance the different stages of sleep data in a sample,and combine multi domain features (time domain, frequency domain, time domain and nonlinear) with random forest classification algorithm for classification and prediction.We compare the classification results of sample equalization processing and non equalization processing, and find that the better classification results are obtained after balancing the processed data.

sleep stage;data imbalance;random forest

TP391.9

ADOI： 10.19358/j.issn.1674- 7720.2016.18.016

2016-04-18)

李玉平(1990-)，通信作者，男，硕士研究生，主要研究方向：智能信息处理。E-mail：liyuping_love@126.com。

夏斌(1975-),男,博士,副教授,硕士生导师，主要研究方向：脑-机接口、云计算及人工智能。