三角形栅格阵列天线方向图的快速计算与优化*

陈海燕,熊祥正,陈凯亚,廖 成

(西南交通大学电磁场与微波技术研究所，成都　610031)

三角形栅格阵列天线方向图的快速计算与优化*

陈海燕**,熊祥正,陈凯亚,廖 成

(西南交通大学电磁场与微波技术研究所，成都610031)

利用有源单元方向图法,提出分别采用小型直线阵和小型三角形栅格阵列外推计算大型三角形栅格阵列天线时域辐射场的两种等效方法,在考虑单元间互耦的同时极大地节约了计算时间。由于两种方法采用的小阵规模和布局不同,导致其计算精度和效率存在较大差异:第一种方法具有较高的计算效率,其计算时间不到仿真软件的4%,但第二种方法计算精度更高,其计算结果与有限积分法软件的仿真结果吻合良好,最大相对误差小于6%,计算时间不到仿真软件的11%。进一步结合第二种方法和田口算法对85元阵列的能量方向图进行优化,在波束宽度的制约条件下获得了较低的副瓣电平,优化时间不到半小时,验证了方法的高效性。

脉冲阵列天线;三角形栅格;时域方向图;低副瓣优化

引用格式:陈海燕，熊祥正，陈凯亚，等.三角形栅格阵列天线方向图的快速计算与优化[J].电讯技术，2016，56(3)：308-312.[CHEN Haiyan，XIONG Xiangzheng，CHEN Kaiya，et a1.Fast ca1cu1ation and oPtimization for triang1e-grid array antenna[J].Te1ecommunication Engineering，2016，56(3)：308-312.]

1　引 言

脉冲天线及其阵列辐射短脉冲，具有超宽带性能，广泛用于雷达探测、目标定位、安全监测以及高速率通信等领域中[1]。目前，脉冲阵列天线的分析与综合技术还处于发展阶段，尤其在考虑互耦情况下，对其辐射方向图的快速计算和优化问题更是一个难点。

自1994年Pozar提出有源单元方向图以来[2]，此方法被广泛用于考虑互耦情况下阵列的求解计算和优化问题。文献[3]利用有源单元方向图来求解大型阵列的散射场，文献[4]进一步结合优化算法实现了阵列辐射场的精确综合。然而，目前阵列的综合方法大多集中在频域，时域的分析和综合方法还不够成熟。但是对于脉冲阵列，时域辐射场更能直观有效地衡量其性能。文献[5]结合时域有限差分法和微遗传算法对TEM喇叭直线阵列的能量方向图进行了优化，虽然考虑了阵列的互耦影响，但在大规模阵列的优化中将耗费大量的时间。文献[6]基于序列二次规划算法，实现了平面阵列时域能量方向图的低副瓣优化，忽略了互耦影响，计算精度无法保证。目前来看，有源单元方向图在阵列天线时域优化方面的研究还鲜有报道，由于有源单元方向图可同时兼顾互耦影响和计算效率，因此，有必要对其在时域方向图的求解和优化方面进行深入研究。

相比于矩形栅格平面阵列天线，三角形栅格平面阵列天线可采用较少的天线单元实现与矩形栅格阵相同的性能，成本更低，具有更大的研究价值。本文结合时域辐射机理，在考虑互耦情况下，提出了两种适用于大型三角形栅格平面阵列时域辐射场快速计算的等效方法，对比分析了两种等效方法的计算效率和计算精度，并结合第二种方法和田口全局优化算法实现了能量方向图的快速优化。

2　方法介绍

有源单元方向图是指在阵列环境中，其他单元接匹配负载，只有该单元激励时得到的方向图。根据时域辐射机理和叠加原理，阵列的远场电场可以表示为所有单元有源方向图的叠加，综合考虑了阵列的互耦影响和阵列环境的影响。

对于一个N元阵列，若采用传统的有源单元方向图法，需对整个空间求解N次，当阵列规模较大时，不仅花费大量的时间，而且对计算机硬件条件提出较高要求，成本较高。研究发现，阵列单元间的互耦影响主要与邻近单元有关，相离越远单元间的互耦越小，随着阵元数目增多，中间单元的辐射场基本可以等价。基于此，可先找出中间单元有源单元方向图开始不变的小型阵列，然后用这个小型阵列的各单元的有源单元方向图来等效相似环境下更大规模阵列中各单元的有源方向图，进而叠加得到大规模阵列的总方向图。

假设阵列沿着xoy面排布，沿x轴排列的定义为行，沿x轴排列的定义为列，主射方向为Z轴正方向，xoz面为E面，yoz面为H面。

2.1第一种等效方法

分别采用2行M元和2列M元(M为奇数)的子阵等效外推Nx行Ny列(Nx＞M，Ny＞M)大型三角形栅格阵列中的H面和E面方向图。H面的等效过如图1所示(E面类同)。

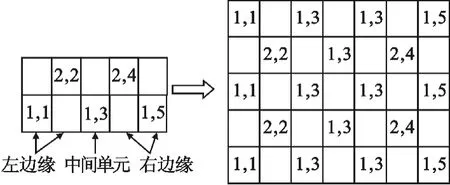
图1　第一种方法等效示意图Fig.1 Equiva1ent diagram of the first method

将阵列划分为左、右边缘列单元和中间列单元，用子阵的左、右边缘列单元以及中间列单元的有源单元方向图分别等效大型阵列对应列中每个单元的方向图，然后叠加计算大型阵列的辐射总场。此方法类似于线阵外推面阵，子阵的求解较为方便快捷。

2.2第二种等效方法

采用M行M列(M为奇数)的小型三角形栅格平面阵列等效外推Nx行Ny列(Nx＞M，Ny＞M)的大型三角形栅格阵列。如图2所示，是用一个5行5列13元的子阵外推一个7行7列25元阵列的等效过程。等效过程分为3步：

第一步 把平面阵列按列分为左、右边缘列单元和中间列单元，用子阵的左、右边缘列和中间列分别等效大型阵列对应的列；

第二步 在每一列的等效过程中，把阵列按行分为上、下边缘行单元和中间行单元，用子阵的上、下边缘行和中间行单元的有源单元方向图分别等效大型阵列对应单元的方向图；

第三步 通过叠加原理求得大型三角栅格平面阵列的时域辐射总场。

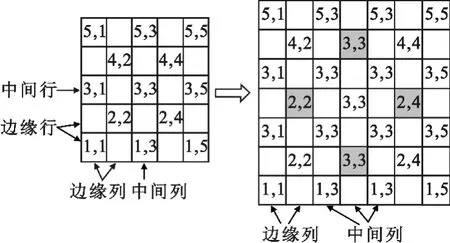
图2　第二种方法等效示意图Fig.2 Equiva1ent diagram of the second method

需要说明的是，由于采用的三角形栅格平面阵列是对称阵列，所以子阵的偶数列(行)单元数目不是奇数，在等效过程中用其邻近单元特殊处理。

另外，对于具有对称性的阵列，在子阵有源单元方向图的计算过程中可利用对称性来进一步减小计算量。例如图2左边的13元子阵，(2，2)、(2，4)、(4，2)、(4，4)这4个是对称单元，只需计算其中一个单元的辐射场，其他3个单元的辐射场可根据对称性得到，计算量明显减小。

3　方法验证

3.1天线单元设计

天线单元采用Viva1di天线，Viva1di天线辐射短脉冲，具有较好的时域保真性能，且具有剖面低、易加工、超宽带以及定向辐射等优点。为了适应集成化通信系统的需求，采用基于有限积分法的商业电磁仿真软件对传统Viva1di天线进行了小型化优化设计。优化后的天线结构如图3所示，介质板采用相对介电常数为4.4的FR4材料，相关尺寸如下：L=30 mm，L1= 14 mm；W=30 mm，W1=26 mm，W2=22 mm，W3= 12 mm，W4=3 mm；S=0.5 mm；R=2 mm；rr=0.2。底端边缘开槽，降低了低频截止点，如图4所示，天线在频段3～11 GHz范围内满足S11＜-10 dB。

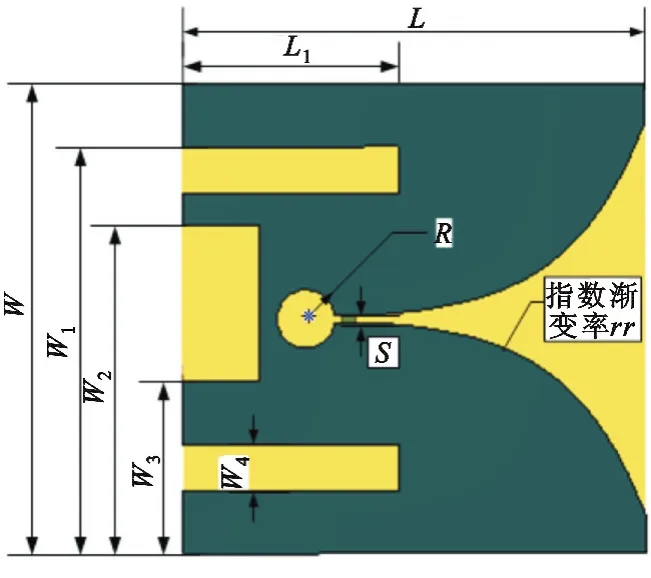
图3　天线单元结构Fig.3 Antenna structure

图4　天线单元的回波损耗Fig.4 The return 1oss of antenna unit

3.2数值结果与分析

首先为了确定子阵的单元数目，采用仿真软件模拟图5(a)所示阵列布局的中间单元的有源单元方向图，逐步增加阵列单元数目，当中间单元的时域方向图基本不变时，即可确定子阵规模。

图5　子阵Fig.5 Subarray

本文采用归一化时域能量方向图来描述脉冲天线的辐射性能，其定义为

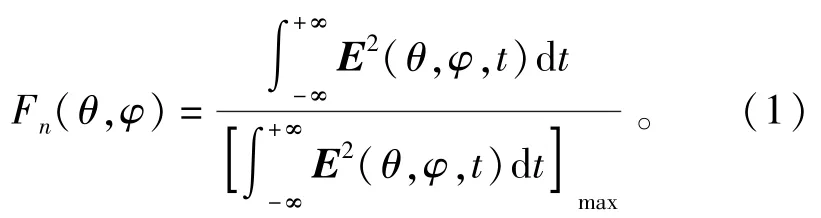
图6给出了随着单元数目增大，中间单元的能量方向图的变化情况。可看到一个单元，也即单元天线的能量方向图与阵列中的有源单元方向图差别较大，3元子阵与5元子阵、7元子阵相比在后瓣存在明显差异，而5元子阵和7元子阵的中间单元的方向图基本一致，因此可采用5元子阵对大型阵列进行等效模拟；同理，采用第二种方法等效时，可采用5行5列的13元子阵来等效，如图5(b)所示。为了验证两种等效方法的可行性，计算了一个13行13列的85元三角形栅格阵列的时域方向图，并与仿真软件的计算结果进行对比分析。对子阵有源单元方向图的提取过程中，利用对称性原理，只需模拟图5方框中各单元的有源单元方向图，进一步减小了计算量。

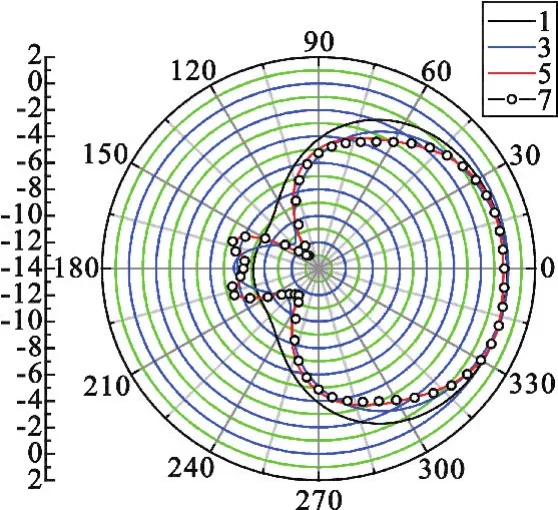
图6　阵列中间单元的有源单元方向图Fig.6 Active e1ement Patten of the center unit in array

图7(a)、(b)分别是H面、E面的时域能量方向图，将两种等效方法的计算结果与仿真结果对比可以看出，第一种等效方法的计算结果只在副瓣和后瓣区域存在误差，而第二种等效方法的计算结果与仿真结果基本一致，计算精度更高，最大相对误差小于6%。表1给出了等效方法和全波仿真的总的计算时间。由表1可以看出，第一种方法的计算时间不到全波仿真时间的4%，第二种方法的计算时间不到全波仿真的11%，显然等效方法大幅度提高了计算效率，其中第一种等效方法计算效率更高。在实际应用中，可根据实际需求选择等效方法。此外，只需对小阵进行一次模拟，保存小阵的有源单元方向图数据，然后结合优化算法和上述等效方法对大型阵列的激励幅度或馈电延时进行优化，可在考虑阵列互耦的情况下实现阵列的快速综合。

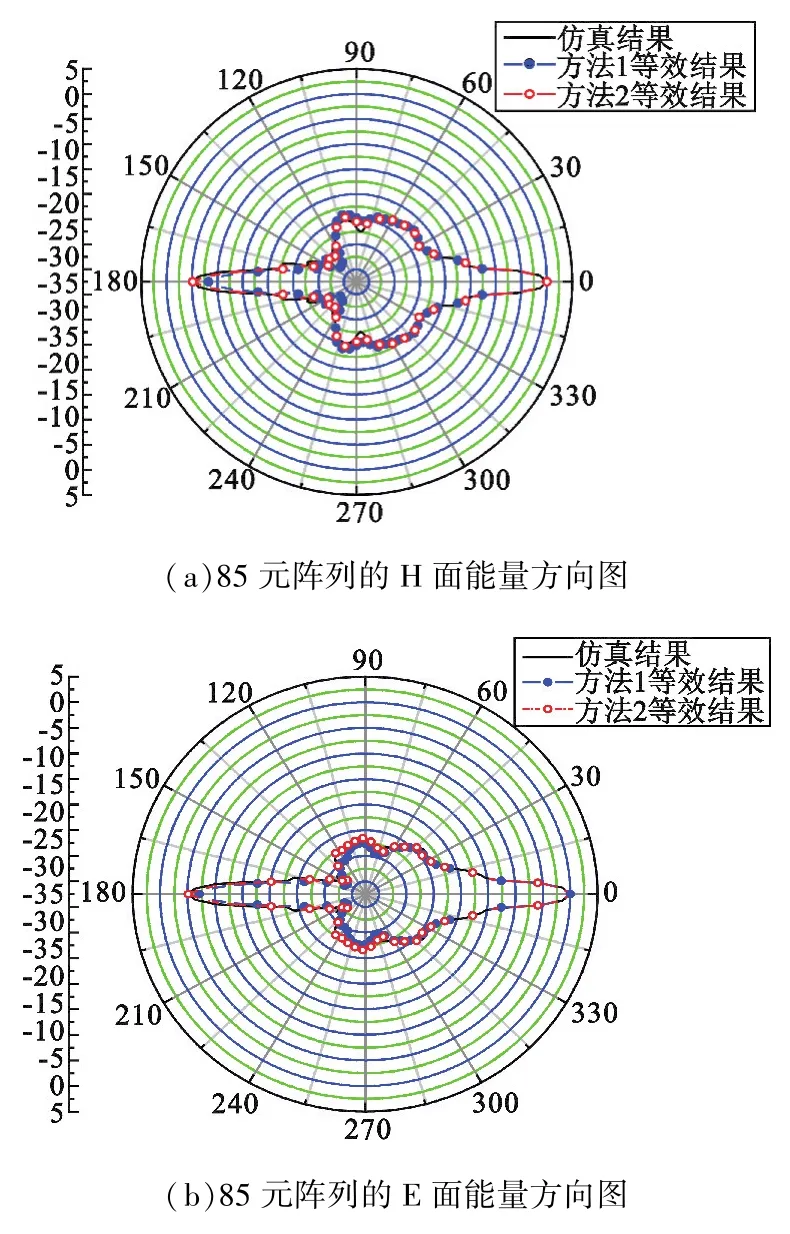
图7　85元阵列的能量方向图Fig.7 Energy Pattern of the 85-e1ement array

表1　计算时间Tab.1 Cost time

4　时域能量方向图优化

田口算法是一种基于正交矩阵的优化算法，以较少的计算量实现多参数的快速寻优，具有实现简单、收敛速度快、全局寻优以及鲁棒性强等优点[7]。

上一节已通过实例验证了两种等效方法在大型三角形栅格平面阵列时域方向图快速计算中的可行性，基于更高的计算精度，采用第二种等效方法，结合田口优化算法对85元阵列进行优化。优化变量为每个单元的激励幅度，由于阵列可分离，E面和H面可分开优化。优化目标为能量方向图的副瓣电平，为了在保证波束宽度基本不变的条件下实现较低的副瓣电平，将适应度函数设置为

式中：SLLmax、BW分别为每一次迭代计算中的最大副瓣电平和波瓣宽度；SLLdes、BWdes分别为目标副瓣电平和波束宽度；w1和w2是权重系数，其中w1= 0.7，w2=0.3，迭代40次后取得较优的结果。图8是85元三角形栅格脉冲阵列的优化结果，其中(a)、(b)分别是E面、H面的能量方向图，优化后E面、H面能量方向图的最大副瓣电平分别降低到-28.43 dB和-26.68 dB，和均匀激励的阵列相比，分别降低了4.3 dB和4.1 dB，同时3 dB波束宽度并没有明显展宽。该方法在限制波束宽度的前提下实现了能量方向图的低副瓣优化。

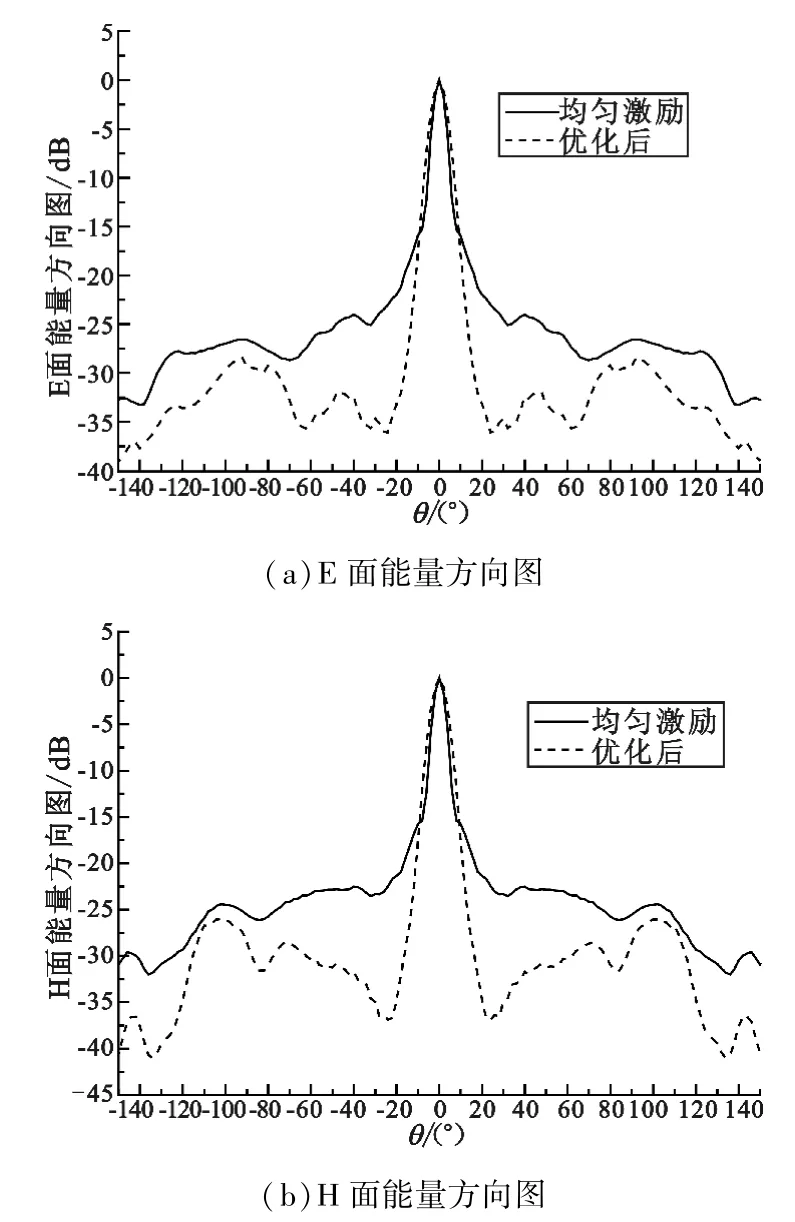
图8　能量方向图的对比Fig.8 ComParison of energy Pattern

5　结束语

本文根据有源单元方向图方法和时域辐射机理，介绍了两种适用于考虑互耦情况下大型三角形栅格平面阵列时域辐射场的快速计算方法。实例表明，两种方法相对于全波仿真明显节约了计算时间，其中第一种方法计算效率更高，而第二种等效方法具有较高的精度。进一步结合第二种计算方法和田口全局优化算法，给出了一种能量方向图的快速优化方案，在波束宽度的制约条件下降低了副瓣电平，优化时间不到半小时。这种方法不仅考虑了阵列的互耦影响，而且显著提高了优化效率，为大型脉冲阵列天线时域方向图的快速优化问题提供了一种精确而高效的解决方案。另外，有源单元方向图结合优化算法在扫描阵列等特殊阵列天线中的应用有待进一步的验证和研究。

[1] LIAO C H，HSU P，CHANG D C.Energy Patterns of UWB antenna arrays with scan caPabi1ity[J].IEEE Transactions on Antennas and ProPagation，2011，59(4)：1140-1147.

[2] POZAR D M.The active e1ement Pattern[J].IEEE Transac

tions on Antennas and ProPagation，1994，42(8)：1176-1178.

[3] ZHANG S，GONG S X，GONG Q，et a1.APP1ication of the active e1ement Pattern method for ca1cu1ation of the scattering Pattern of 1arge finite arrays[J].IEEE Antennas and Wire1ess ProPagation Letters，2011(10)：83-86.

[4] 周明，张树人，张浩斌.8～12 GHz Viva1di槽缝天线阵设计及综合[J].中国电子科学研究院学报，2014，5 (4)：376-380.

ZHOU Ming，ZHANG Shuren，ZHANG Haobin.Design and synthesis of 8～12 GHz Viva1di s1ot antenna arrays [J].Journa1 of China Academy of E1ectronic Information Techno1ogy，2014，5(4)：376-380.(in Chinese)

[5] 覃延明，廖成，魏涛，等.超宽带TEM喇叭天线阵列的微遗传算法优化[J].电波科学学报，2008，23(2)：352-355.

QIN Yanming，LIAO Cheng，WEI Tao，et a1.OPtimization of u1tra-wide band TEM horn antenna array based on micro-genetic a1gorithm[J].Chinese Journa1 of Radio Science，2008，23(2)：352-355.(in Chinese)

[6] MALDONADO R A，PANDURO M A，BOCIO D C.Twodimensiona1 time-domain antenna arrays for steerab1e energy Pattern with 1ow side 1obe 1eve1[C]//Proceedings of 2014 8th EuroPean Conference on Antennas and ProPagation(EuCAP).Hague：IEEE，2014：1513-1517.

[7] WENG W C，YANG F，ELSHERBENI A Z.Linear antenna array synthesis using Taguchi's method：a nove1 oPtimization technique in e1ectromagnetics[J].IEEE Transactions on Antennas and ProPagation，2007，55(3)：723-730.

陈海燕(1989—)，女，甘肃张掖人，2013年于西南交通大学获学士学位，现为硕士研究生，主要研究方向为天线理论与设计；

CHEN Haiyan was born in Zhangye，Gansu Province，in 1989.She received the B.S.degree from Southwest Jiaotong University in 2013.She is now a graduate student.Her research concerns antenna theory and design.

Emai1：haiyan¯chen111@163.com

熊祥正(1964—)，男，重庆人，现为西南交通大学教授，主要研究方向为微波电路设计和电磁兼容；

XIONG Xiangzheng was born in Chongqing，in 1964.He is now a Professor.His research concerns microwave circuit design and e1ectromagnetic comPatibi1ity.

陈凯亚(1971—)，男，四川人，博士，讲师，主要研究方向为微波电路和信号处理；

CHEN Kaiya was born in Sichuan Province，in 1971.He is now a 1ecturer with the Ph.D.degree.His research concerns microwave circuit，signa1 Processing.

廖 成(1964—)，男，重庆人，现为西南交通大学教授、博士生导师，主要研究方向为计算电磁学、电磁兼容和天线原理与设计。

LIAO Cheng was born in Chongqing，in 1964.He is now a Professor and a1so the Ph.D.suPervisor.His research concerns comPutationa1 e1ectromagnetics，e1ectromagnetic comPatibi1ity，and antenna theory and techno1ogy.

Emai1：c.1iao@swjtu.edu.cn

Fast Calculation and Optimization for Triangle-grid Array Antenna

CHEN Haiyan，XIONG Xiangzheng，CHEN Kaiya，LIAO Cheng
(Institute of E1ectromagnetics，Southwest Jiaotong University，Chengdu 610031，China)

According to the active e1ement Pattern theory，this PaPer ProPoses two methods for fast ca1cu1ating the time-domain radiation Patterns of 1arge arrays.With the methods，time-domain ana1ysis Prob1ems of a 1arge triang1e-grid array are resPective1y converted into Prob1ems of a sma11 1inear array and a triang1e -grid one.Meanwhi1e，the mutua1 couP1ing is considered and the comPutationa1 cost is reduced great1y. The different size and 1ayout of the sma11 arrays in two methods 1eads to a great difference in Precision and efficiency.Resu1ts show that the first method obtains a higher efficiency and the time cost is 1ess than 4% of that simu1ated by the finite integra1 method.However，the second method achieves a better Precision，whose resu1ts agree we11 with the simu1ation resu1ts and the maximum re1ative error is 1ess than 6%，and comPutation time is 1ess than 11%of the simu1ation time.Furthermore，combined with the second method，Taguchi a1gorithm is adoPted for 85-e1ement array energy Patterns oPtimization，and the side 1obe 1eve1 is reduced whi1e the beam width is 1imited.What's more，the oPtimization time is 1ess than ha1f an hour，which verifies the va1idity of the method.

Pu1se array antenna；triang1e-grid；time-domain radiation Pattern；1ow side 1obe oPtimization

The Key Laboratory of High Power Microwave Techno1ogy Program(2014H01022)

TN821

A

1001-893X(2016)03-0308-05

10.3969/j.issn.1001-893x.2016.03.013

2015-07-29;

2015-10-30 Received date:2015-07-29;Revised date:2015-10-30

高功率微波技术重点实验室自主基础研究项目(2014H01022)

**通信作者:haiyan¯chen111@163.com Corresponding author:haiyan¯chen111@163.com