裂缝性油藏改进多重子区域模型
2016-10-28黄朝琴樊冬艳张建光
严 侠, 黄朝琴, 姚 军, 李 阳, 樊冬艳, 张建光
(1.中国石油大学石油工程学院,山东青岛 266580; 2.中国石化油田勘探开发事业部,北京 100728)
裂缝性油藏改进多重子区域模型
严侠1, 黄朝琴1, 姚军1, 李阳2, 樊冬艳1, 张建光1
(1.中国石油大学石油工程学院,山东青岛 266580; 2.中国石化油田勘探开发事业部,北京 100728)
针对现有多重子区域模型在计算裂缝单元间等效传导系数时存在的问题,采用超样本技术和体积平均法对其进行改进,改进后的模型可以有效考虑周围区域介质对裂缝单元间等效传导系数的影响,同时可以得到全张量形式的等效渗透率,在此基础上运用模拟有限差分方法构造考虑全张量形式等效渗透率的数值计算格式进行模型求解。针对不同裂缝性油藏,通过数值算例对改进模型和原始模型的准确性进行对比分析。结果表明:改进模型的计算精度比原始模型有较大提高,与离散裂缝模型参考结果基本一致,同时其计算效率高于离散裂缝模型。
裂缝性油藏; 离散裂缝模型; 超样本技术; 双重介质模型; 模拟有限差分
引用格式:严侠,黄朝琴,姚军,等. 裂缝性油藏改进多重子区域模型[J].中国石油大学学报(自然科学版),2016,40(3):121-129.
YAN Xia, HUANG Zhaoqin, YAO Jun, et al. An improved multiple sub-region method for flow simulation of fractured reservoirs[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(3):121-129.
随着勘探开发程度的不断加深,近年来新探明的油藏类型越来越复杂,裂缝性油藏探明储量不断增加[1]。致密油气和页岩气等非常规油气资源须压裂后方可商业开采[2],压裂后也为裂缝性油气藏。在此形势下,裂缝性油藏数值模拟得到广泛的重视,出现了一系列优秀的裂缝性油藏数学模型,如等效连续介质模型[3-4]、双重介质模型[5-8]、离散裂缝模型[9-12]等。等效连续介质模型以等效渗透率为基础,用连续介质方法描述渗流问题,该模型计算效率较高并且在理论以及方法上都有雄厚的基础和经验,但该模型中没有考虑裂缝与基岩间窜流,不能准确模拟低渗油气藏开发中的非稳态过程;离散裂缝模型将裂缝显式表征,基于裂缝内流量等效原理将裂缝进行降维,属于宏观尺度的精细模型,能准确刻画出裂缝性油藏中的流动特征,但受目前计算机硬件和数值模拟技术的制约,尚不能用于油田尺度的大规模流动数值模拟;双重介质模型能在一定程度上反映裂缝性油藏中的裂缝系统优先流特征,并考虑裂缝系统和基岩系统间的窜流,比较符合实际且计算效率较高,因此被广泛用于实际油藏数值模拟。双重介质模型中的关键问题是如何求取裂缝与基岩系统间的窜流系数,针对这一问题,国内外众多学者进行了大量研究[13-14]。大部分研究都着眼于采用对实际模型简化近似结合解析方法确定窜流系数,因此采用这类方法处理实际复杂非稳态问题时计算结果常常有较大误差。对此,M.Karimi-Fard等[15]借鉴MINC模型的思想提出一种新的双重介质模型[16-17](多重子区域模型,multiple subregion (MSR) method),该模型以离散裂缝模型为基础,通过数值求解小范围的离散裂缝模型获取基岩与裂缝间的窜流系数以及各单元的等效参数,无须对实际油藏结构进行简化近似,适用于任何复杂结构裂缝性油藏,然而该模型在获取裂缝单元间等效传导系数时,仅取相邻的两个网格单元采用封闭定压边界条件结合流量等效进行计算,忽略了周围区域介质的影响,并且单元中裂缝的几何结构通常较复杂,其等效渗透率应该是全张量形式,而采用目前方法进行计算相当于只考虑了对角项,因此该模型仍存在一定的缺陷。笔者采用超样本技术和体积平均法对MSR模型中裂缝单元间等效传导系数的求解方法进行改进,改进后的模型可以有效考虑周围区域介质的影响,同时可以得到全张量形式的等效渗透率,针对裂缝单元全张量形式的等效渗透率,运用模拟有限差分方法[18]构造相应的传导系数矩阵进行数值求解。
1 模型基本原理
MSR模型是一种由小尺度离散裂缝模型等效升级得到的大尺度双重介质模型,裂缝系统是流体的主要流动通道,基岩系统作为流体的主要储存空间。模型的主要计算步骤如下:
(1)对整体裂缝性油藏进行粗网格划分(通常采用笛卡尔正交网格),图1(a)。
(2)在每个粗网格内建立离散裂缝模型,划分非结构网格并进行流动模拟(封闭边界,裂缝处为注入采出端),根据拟稳态时的等压线分布将每个粗网格划分为若干个子区域(同一压力范围内的非结构网格单元属于同一子区域,子区域划分数量取决于精度要求,一般取6个左右即可[16],本文中所有粗网格中子区域数均取6),图1(b)。
(3)计算各粗网格中子区域单元的物性参数及相邻子区域单元之间的传导系数,子区域单元间的连通关系如图1(c)所示。
(4)计算各粗网格之间的传导系数,原始MSR模型取相邻的两个网格单元采用封闭定压边界条件结合流量等效计算网格之间的传导系数,如图2所示,改进的MSR模型先计算每个粗网格的等效渗透率张量,以此为基础构造相应的传导系数。

图1 MSR模型网格划分及子区域连通关系示意图Fig.1 Schematic for coarse meshing and connected relations of sub-regions
(5)根据各单元间的连通关系构建整体数值计算格式并求解,模型中各单元间的相互连通关系如图3所示,宏观流动主要通过各粗网格内的第一个子区域(裂缝单元F),各粗网格内的基岩单元M不与其他粗网格中的任何单元相连。图3中,第一个下标表示粗网格单元编号,第二个下标表示子区域单元编号(如果只有一个下标则表示粗网格单元编号)。
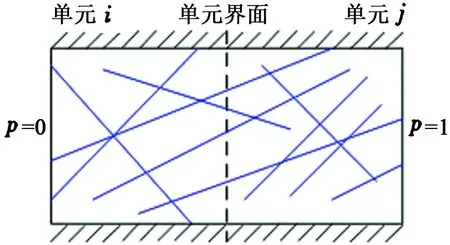
图2 裂缝单元间等效传导系数计算示意图Fig.2 Schematic for calculation of equivalent conduction coefficient between facture elements
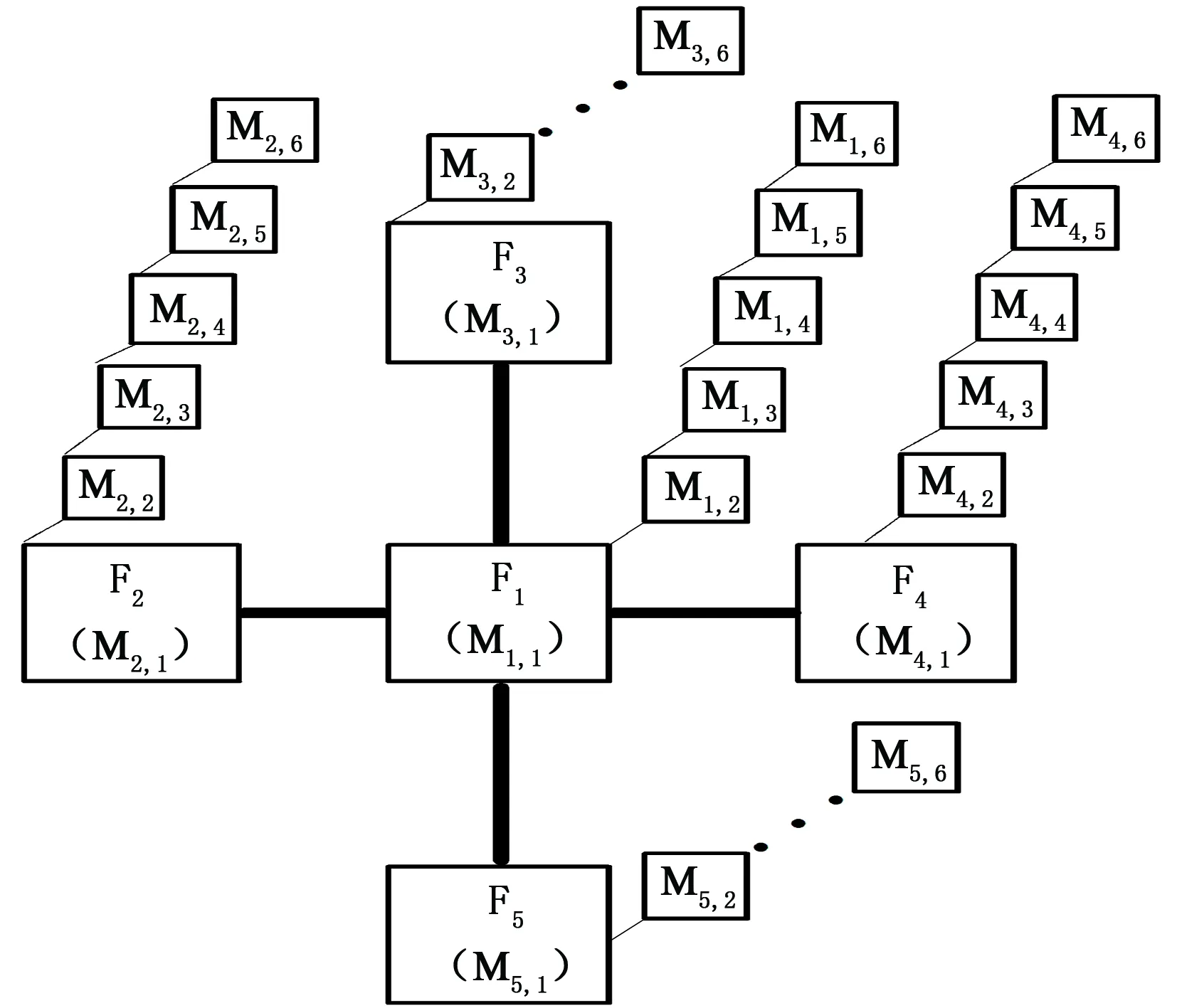
图3 MSR模型中各单元间相互连通关系示意图Fig.3 Schematic for connected relations of units
1.1子区域单元物性参数及相互之间传导系数计算
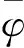
(1)

(2)
式中,下角j表示属于子区域Ωi,k中的第j个小非结构网格单元;∂ρj/∂t项在拟稳态时为常数。
在计算各子区域单元间的流量交换时,须从最外面的单元开始,因为该单元只有一个相邻单元,如图1(c)中子区域6所示。此时,单元间的流量交换量Qn-1,n,k等于单元内流体质量增加量An,k。对于其他子区域单元,从外向内依次计算即可求得相互之间的流量交换量,
Qi,i+1,k=Ai+1,k-Qi+1,i+2,k,i=1,…,n-2 .
(3)
由此,可以计算出子区域单元间的传导系数:
(4)
1.2裂缝单元等效渗透率计算
对裂缝单元进行超样本处理,首先获取每个目标单元的超样本单元;然后在超样本单元内建立离散裂缝模型并进行有限元数值求解,获取超样本单元内的压力和速度场;最后采用体积平均法计算目标单元内的速度和压力梯度的平均值,以此为基础根据达西定律求取目标单元的等效渗透率。此时求得的等效渗透率中存在基岩的贡献,由于基岩渗透率远小于裂缝单元等效渗透率,因此该渗透率可以作为裂缝单元等效渗透率的有效近似值[16]。
1.2.1超样本技术
本文中的超样本技术不同于图像信息处理中的超采样技术,是多尺度有限元和油藏尺度升级中一种提高计算精度的方法[19-20],具体是指在计算某个单元(目标单元)的等效渗透率时,将该单元周围的区域考虑进来形成一个大的超样本单元,这样可以有效考虑周围区域对等效渗透率的影响。以二维系统为例,如图4所示,当网格在角落时,超样本单元中包含4个网格;当网格在边界上时,超样本单元中有6个网格;当网格在内部时,超样本单元包含9个网格。需要注意的是,超样本单元选取的范围对等效结果有一定影响,选取的范围越大,计算精度越高,在保证满足计算精度要求的情况下为提高计算效率,取了目标网格周围的一层网格。
超样本技术的优点在于:计算裂缝单元等效渗透率时考虑周围区域的影响,可以在目标单元周围间接构造更为合理的边界条件,避免人为施加边界条件(通常不准确)。这一优点对于全局贯通的大裂缝等效渗透率计算最为明显,因为此时裂缝单元的表征单元体(REV)已不存在,单元的等效渗透率并非其本质属性,其值受计算时采用的边界条件影响,采用超样本技术间接构造合理的边界条件,计算结果更为准确。

图4 超样本技术示意图Fig.4 Schematic of oversampling technology
1.2.2等效渗透率计算
在超样本单元内结合封闭定压边界条件建立离散裂缝模型,划分三角网格,采用有限单元法进行求解(具体的求解过程参考文献[21]),根据求得的压力及速度场,运用体积平均法求取目标网格上的速度和压力梯度的体积平均值[20]:
(5)
(6)
式中,j=x,y,表示定压边界施加的坐标轴方向;Vb为目标网格的体积;ul和(p)l分别为目标网格中第l个三角网格单元的速度和压力梯度;Vl为第l个三角网格单元的体积;N为目标网格中三角网格单元的总数。对于二维问题则相当于面积平均,以二维问题的计算过程为例,三维计算过程与之类似。
〈u〉j和〈p〉j由两部分组成,分别为x和y方向,根据达西定律可得到以下方程组:
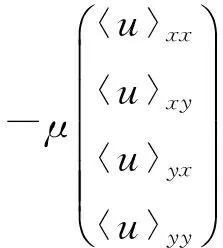
(7)
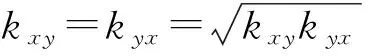
2 数学模型的建立及求解
为研究和书写方便,基于二维单相流问题阐述数值方法的数学模型和求解过程。假设流体流动过程恒温,仅考虑流体的压缩性,基岩系统和裂缝系统中的流体流动均满足达西定律。
裂缝系统数学模型为
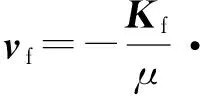
(8)
(9)
式中,vf为裂缝渗流速度,m/s;Kf为裂缝渗透率张量,μm2;μ为流体黏度,mPa·s;qf为裂缝单位体积上的源汇项,s-1;Vf为裂缝单元的体积;cft为裂缝中的综合压缩系数,Pa-1。
根据图2中各单元间的连通关系可知:基岩部分的流动可以看成是由基岩流向裂缝的一维流动,同时基岩各网格单元的物性参数及单元间的传导系数均已知,因此直接给出基岩系统数学模型的空间离散形式为
Ti,i+1(pmi+1-pmi)-Ti,i-1(pmi-pmi-1)=
(10)
其中
qmf=Tmf(pm-pf).
式中,pm和pf分别为基岩和裂缝的压力,Pa;Vm为基岩单元的体积,m3;qm为基岩单位体积上的源汇项,s-1;cmt为基岩的综合压缩系数,Pa-1;Tmf为基岩单元与裂缝单元间的传导系数,m3/(Pa·s);δmf为当基岩单元与裂缝相邻时取1,其余情况为0;T为基岩单元间的传导系数,m3/(Pa·s)。
2.1裂缝系统采用模拟有限差分离散


图5 模拟有限差分网格单元分析示意图Fig.5 Schematic of grid analysis for MFD
裂缝网格边界面上的法向渗流速度vf与压力梯度pf之间关系为
vf=Tfi·(eipfei-pff).
(11)
其中
vff=[vff1,vff2,…,vffn]T,ei=[1,…,1]T.
式中,Tfi为裂缝网格的传导矩阵;n为单元Ωi的边界面数。
模拟有限差分方法的关键问题是获取矩阵Tfi。假设压力在裂缝网格内呈线性变化,即pf=af·x+bf,显然,

(12)
同时,pfei-pffk=af·(xi-xk),结合式(11)和(12)可得:
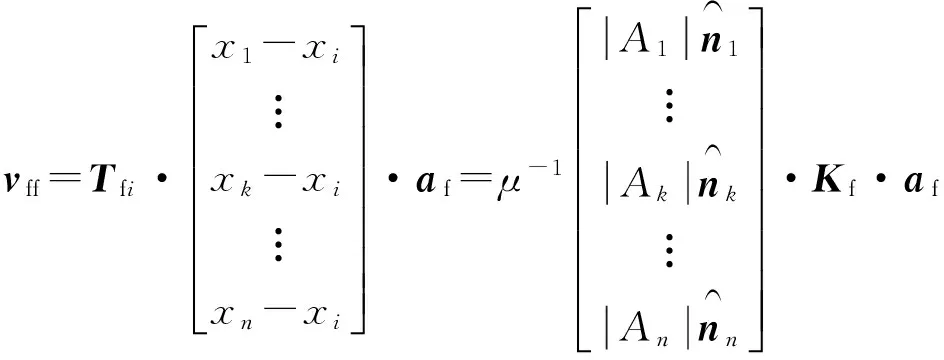
(13)
其中


通过方程(13)求得传导矩阵为
(14)
其中,T2X=0,为保证Tfi矩阵逆的存在,可应用Brezzi-Lipnikov-Simoncini定理[22]构造T2矩阵:
(15)
其中
Q=orth(AX).
对于方程(9),直接在网格单元上积分并运用散度定理:
(16)
考虑单元边界面上的速度连续条件,结合方程(11)和(16),得到裂缝部分模拟有限差分的数值计算格式为
(17)
其中
vf=[vffk], pf=[pfei], πf=[pffk],ff=[ffi],

显然,方程(17)中的第一行对应于方程(8)达西定律定律,第二行对应于方程(9)质量守恒定律,第三行则表征了单元边界面上的法向速度连续性条件。方程(17)的系数矩阵表达式为

式中,Ne为裂缝网格单元总数;Ii=En。
2.2整体计算格式
将基质部分和裂缝部分的数值计算格式组装到一起,得到改进MSR模型的整体计算格式为

其中
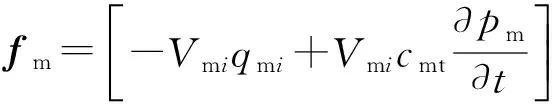
3 算例分析
3.1模型验证
图6(a)为一裂缝完全连通的理想裂缝性油藏,180m×180m,划分9×9粗网格后如图6(b)所示,每个粗网格中的裂缝结构完全一致,整个油藏可以看成由若干个性质一样的单元重复排列形成。此时,是否采用超样本技术对每一个单元的等效渗透率没有影响,并且根据粗网格单元内的裂缝结构可以得出其等效渗透率为对角张量形式。对于图6(a)所示的裂缝性油藏,改进模型与原始MSR模型的计算结果应当一致,可以用来验证本文模型的正确性。
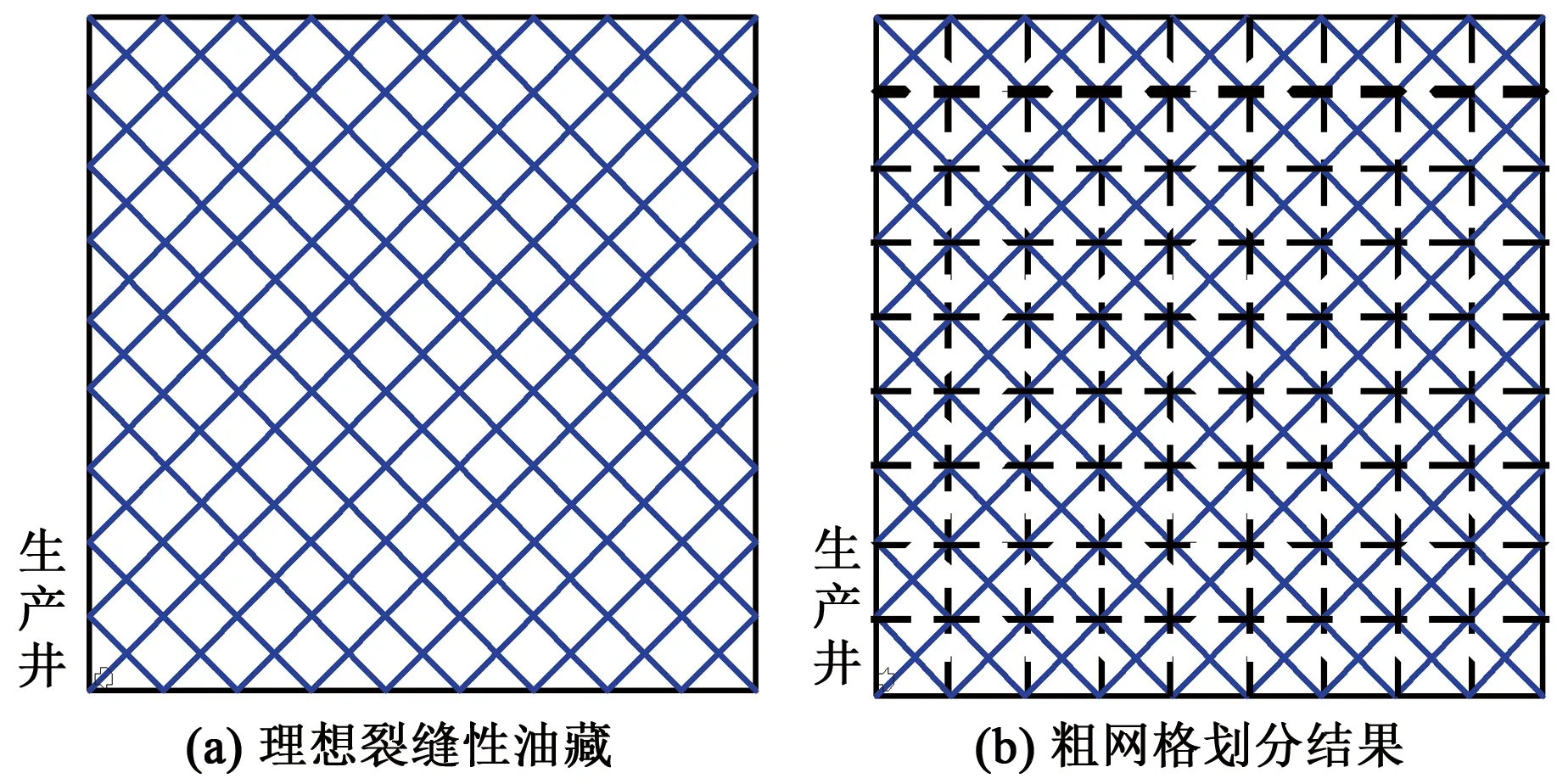
图6 理想裂缝性油藏及粗网格划分示意图Fig.6 Schematic of ideal fractured reservoir and coarse grids
对图6中的裂缝性油藏分别采用离散裂缝模型(DFM)、改进模型以及原始MSR模型进行单井定压弹性开采模拟,基本参数如下:基岩渗透率为1×10-2μm2,基岩孔隙度为0.2,裂缝渗透率为8.33×104μm2,裂缝孔隙度为1,裂缝开度为0.001 m,流体黏度为4 mPa·s,流体压缩系数为2×10-9Pa-1,初始地层压力为20 MPa,井底流压为5 MPa,井筒半径为0.1 m。模拟结果(产量曲线)如图7所示。从图7中可以看出,3种方法计算得到的产量曲线完全重合,验证了改进模型的正确性。
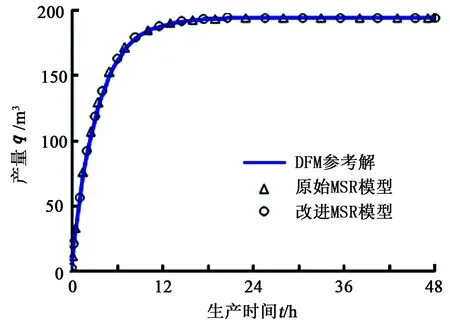
图7 裂缝性油藏弹性开采产量曲线Fig.7 Elastic driving production curves of ideal fractured reservoir
3.2二维复杂裂缝性油藏
图8(a)为240 m×240 m复杂裂缝性油藏,划分8×8的粗网格,如图8(b)所示。油藏基本参数与3.1节算例一致。分别采用离散裂缝模型(DFM)、改进模型、采用超样本的等效连续介质模型以及原始MSR模型进行单井定压弹性开采模拟,模拟结果(产量曲线)如图9所示。
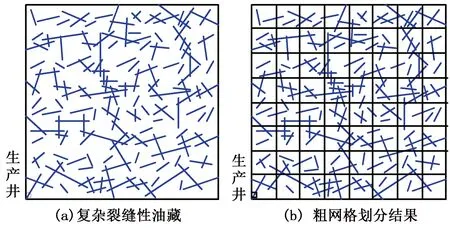
图8 复杂裂缝性油藏及粗网格划分示意图Fig.8 Schematic of complex fractured reservoir and coarse grids
从图9(a)中可看出:改进模型的模拟结果与离散裂缝模型参考结果基本一致,而原始MSR模型由于在计算裂缝单元间传导系数时不准确,导致其计算结果误差很大;在开采时间较长的情况下,采用超样本的等效连续介质模型模拟结果与改进模型结果吻合很好。从图9(b)中可看出:在开采早期,改进模型模拟结果与离散裂缝模型参考结果仍然保持一致,而等效连续介质模型模拟结果则有较大偏差,这是由于等效连续介质模型不能准确刻画开采早期基岩与裂缝间的非稳态窜流特征所致。 本文中改进模型可以准确模拟复杂裂缝性油藏开采的整个过程。

图9 复杂裂缝性油藏弹性开采产量曲线Fig.9 Elastic driving production curves of complex fractured reservoir
3.3三维裂缝性油藏
考虑如图10(a)所示的三维裂缝性油藏,油藏中部分裂缝垂直贯穿整个油藏,油藏尺寸为200 m×100 m×40 m,划分10×5×2的粗网格,该油藏的基本参数与3.1节算例一致。图10(b)为最上层裂缝单元x方向等效渗透率场。分别采用离散裂缝模型和改进模型进行弹性开采模拟,采出井位于油藏的左下角,模拟结果如图11所示。
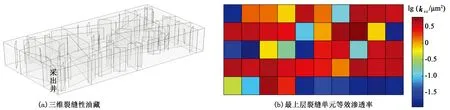
图10 三维裂缝性油藏及等效渗透率场Fig.10 Schematic of 3D fractured reservoir and equivalent permeability
从图11中可看出,对于本算例中三维裂缝性油藏弹性开采,改进MSR模型的模拟结果与离散裂缝模型参考结果基本一致,而原始MSR模型的计算结果误差较大。
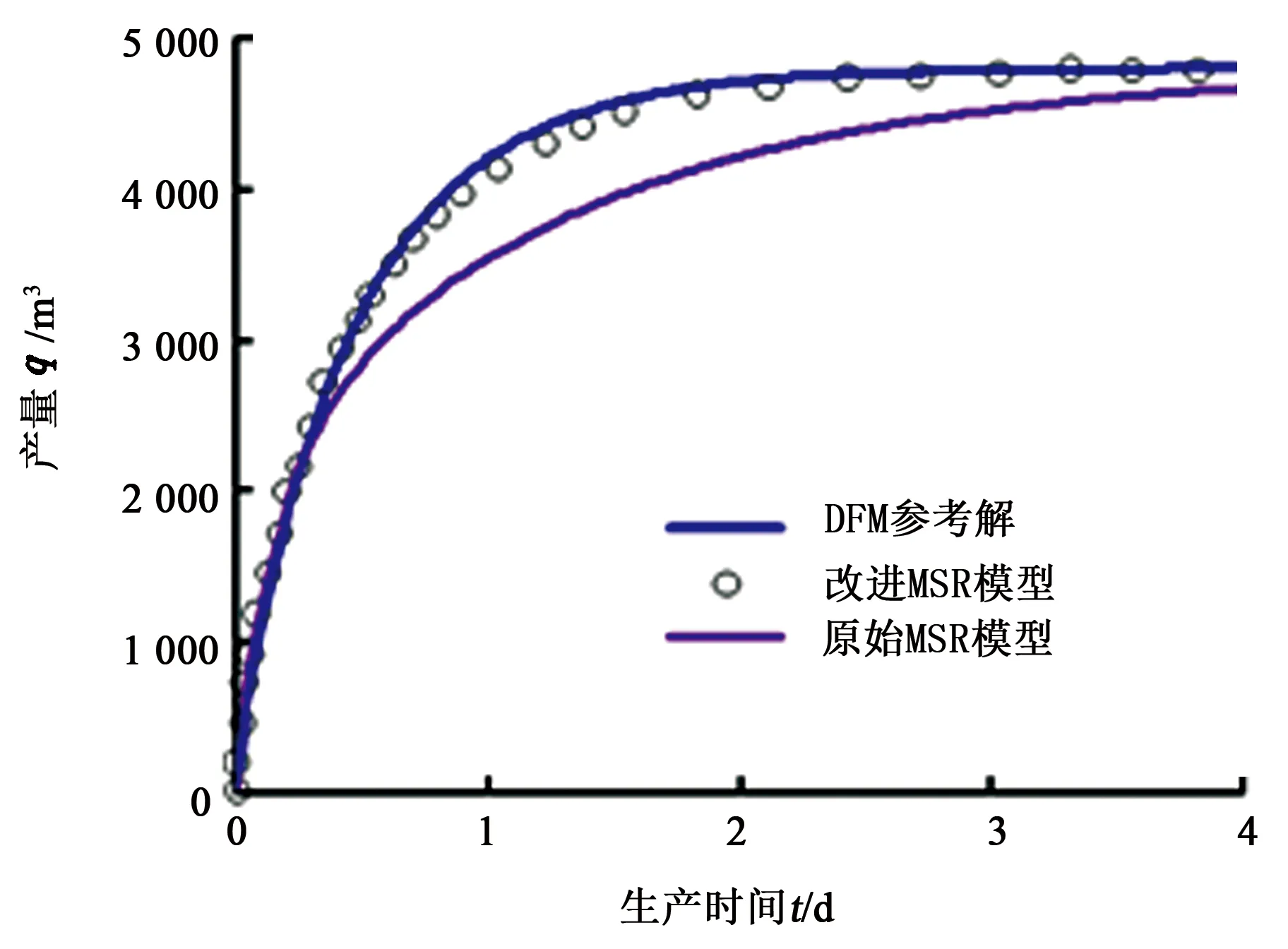
图11 三维裂缝性油藏弹性开采产量曲线Fig.11 Elastic driving production curves of 3D fractured reservoir
以上算例表明,提出的改进模型的计算精度较原始MSR模型有较大提高,与离散裂缝模型基本一致。该模型与离散裂缝模型相比,无须对油藏进行整体非结构网格划分与求解(对于实际三维裂缝性油藏,进行整体非结构网格划分及求解的计算量过大,目前难以实现),而是采用化整为零的思想先将油藏划分为若干个小的粗网格单元,在每个粗网格内进行小范围的非结构网格划分及离散裂缝流动模拟,根据模拟结果划分粗网格中子区域单元并求取各子区域单元的等效参数及相互之间的传导系数,以此建立双重介质模型进行整体数值模拟,可以有效降低裂缝性油藏网格划分及求解的复杂度。
4 结 论
(1)多重子区域模型是一种广义双重介质模型,该模型通过数值求解小范围的离散裂缝模型获取基岩与裂缝各单元的等效物性参数及相互之间的传导系数,以此为基础进行裂缝性油藏流动模拟。该模型与常规双重介质模型相比,无须对实际裂缝性油藏几何结构进行简化近似,适用于任何复杂结构的裂缝性油藏。
(2)采用超样本技术和体积平均法对多重子区域模型进行改进,改进模型可以有效考虑周围区域介质对裂缝单元间等效传导系数的影响,同时可以得到全张量形式的等效渗透率,在此基础上运用模拟有限差分方法构造考虑全张量形式等效渗透率的传导系数矩阵进行数值求解。算例分析证明了改进模型的正确性与优越性。
[1]袁士义,宋新民,冉启全.裂缝性油藏开发技术[M].北京:石油工业出版社,2004:1-3.
[2]张磊,康钦军,姚军,等.页岩压裂中压裂液返排率低的孔隙尺度模拟与解释[J].科学通报,2014,59(32):3197-3203.
ZHANG Lei, KANG Qinjun, YAO Jun, et al. The explanation of low recovery of fracturing fluid in shale hydraulic fracturing by pore-scale simulation[J]. Chinese Science Bulletin, 2014,59(32):3197-3203.
[3]SNOW D. Anisotropic permeability of fractured media[J]. Water Resources Research, 1969,5(6):1273-1289.[4]ODA M. Permeability tensor for discontinuous rock masses[J]. Geotechnique, 1985,35(4):483-495.
[5]BARENBLATT G I, ZHELTOV I P, KOCHINA I N. Basic concept in the theory of homogeneous liquids in fissured rocks[J]. Journal of Applied Mathematics and Mechanics, 1960,24(5):1286-1303.
[6]KAZEMI H, PORTERFIELD K, ZEMAN P. Numerical simulation of water-oil flow in naturally fractured reservoirs[J]. Old SPE Journal, 1976,16:317-326.
[7]LEMONNIER P, BOURBIAUX B. Simulation of naturally fractured reservoirs state of the art, part 1: physical mechanisms and simulator formulation[J]. Oil & Gas Science and Technology-Revue de Institute Francais du Petrole, 2010,65:239-262.
[8]LEMONNIER P, BOURBIAUX B. Simulation of naturally fractured reservoirs, state of the art, part 2: matrix-fracture transfers and typical features of numerical studies[J]. Oil & Gas Science and Technology-Revue de Institute Francais du Petrole, 2010,65:263-286.
[9]KARIMI-FARD M, DURLOFSKY L J, AZIZ K. An efficient discrete-fracture model applicable for general-purpose reservoir simulators[J]. SPE Journal, 2004,9(2):227-236.
[10]黄朝琴,高博,王月英,等.基于模拟有限差分法的离散裂缝模型两相流动模拟[J].中国石油大学学报(自然科学版),2014,38(6):97-105.
HUANG Zhaoqin, GAO Bo, WANG Yueying, et al. Two-phase simulation of discrete fracture model by using mimetic finite difference method[J]. Journal of China University of Petroleum (Edition of Natural Science), 2014,38(6):97-105.
[11]严侠,黄朝琴,姚军,等.基于模拟有限差分的嵌入式离散裂缝数学模型[J].中国科学技术科学,2014,44(12):1333-1342.
YAN Xia, HUANG Zhaoqin, YAO Jun, et al. The embeded discrete fracture model based on mimetic finite difference method[J]. Science China Technological Sciences, 2014,44(12):1333-1342.
[12]YAN X, HUANG Z, YAO J, et al. An efficient embedded discrete fracture model based on mimetic finite difference method[J]. Journal of Petroleum Science and Engineering, 2016, 145: 11-21.
[13]周德华,葛家理.复杂裂缝油藏中窜流函数的建立[J].油气采收率技术,2000,7(2):30-32.
ZHOU Dehua, GE Jiali. The establishment of interporosity flow function in complex fracture reservoir[J]. Petroleum Geology and Recovery Efficiency, 2000,7(2):30-32.
[14]舒卫兵,许鹤华,刘唐伟,等.低渗透裂缝性油气藏非稳态窜流因子研究[J].力学学报,2014,46(1):70-77.
SHU Weibing, XU Hehua, LIU Tangwei, et al. Research on nonsteady shape factor of cross flow in low permeability fractured reservoirs[J]. Chinese Journal of Theoretical and Applied Mechani, 2014,46(1):70-77.
[15]PRUESS K. A practical method for modeling fluid and heat flow in fractured porous media[J]. Society of Petroleum Engineers Journal, 1985,25(1):14-26.
[16]KARIMI-FARD M, GONG B, DURLOFSKY L J. Generation of coarse-scale continuum flow models from detailed fracture characterizations[J]. Water Resources Research, 2006,42(10):1-13.
[17]GONG B, KARIMI-FARD M, DURLOFSKY L J. Upscaling discrete fracture characterizations to dual-porosity, dual-permeability models for efficient simulation of flow with strong gravitational effects[J]. SPE Journal, 2008,13(1):58-67.
[18]LIPNIKOV K, MANZINI G, SHASHKOV M. Mimetic finite difference method[J]. Journal of Computational Physics, 2014,257:1163-1227.
[19]薛禹群,叶淑君,谢春红,等.多尺度有限元法在地下水模拟中的应用[J].水利学报,2004(7):7-13.
XUE Yuqun, YE Shujun, XIE Chunhong, et al. Application of multi-scale finite element method to simulation of groundwater flow[J]. Journal of Hydraulic Engineering, 2004(7):7-13.
[20]DURLOFSKY L J. Upscaling and gridding of fine scale geological models for flow simulation: 8th International Forum on Reservoir Simulation Iles Borromees, Stresa, Italy, 2005[R]. Leoben, Austria,2005.
[21]黄朝琴,姚军,王月英,等.基于离散裂缝模型的裂缝性油藏注水开发数值模拟[J].计算物理,2011,28(1):41-49.
HUANG Zhaoqin, YAO Jun, WANG Yueying, et al. Numerical simulation on water flooding development of fracture reservoirs in a discrete-fracrure model[J]. Chinese Journal of Computational Physics, 2011,28(1):41-49.
[22]BREZZI F, LIPNIKOV K, SIMONCINI V. A family of mimetic finite difference methods on polygonal and polyhedral meshes[J]. Mathematical Models and Methods in Applied Sciences, 2005,15(10):1533-1551.
(编辑李志芬)
An improved multiple sub-region method for flow simulation of fractured reservoirs
YAN Xia1, HUANG Zhaoqin1, YAO Jun1, LI Yang2, FAN Dongyan1, ZHANG Jianguang1
(1.SchoolofPetroleumEngineeringinChinaUniversityofPetroleum,Qingdao266580,China;2.DepartmentofOilfieldExploration&Development,SINOPEC,Beijing100728,China)
An improved multiple sub-region method (MSR) for flow simulation of a fractured reservoir was proposed by using an over-sampling technique and a volume averaging method. The improved MSR method can reflect the strong anisotropy in fractures and can effectively simulate the effects of nearby sub-region on the transmissibility of the fractures. A mimetic finite difference method (MFD) was used for the numerical solution, which has excellent local conservation features and good applicability for the complex unstructured grid and permeability tensors. Several case studies were conducted to verify the accuracy and applicability of the improved method. The results obtained using the improved model agree well with those obtained using a conventional discrete fracture model, and the calculation efficiency of the improved model is higher than that of the discrete fracture model.
fractured reservoir; discrete fracture model; oversampling technique; double media model; mimetic finite difference method
2015-07-21
国家重点基础研究发展计划(2011CB201004);国家自然科学基金项目(51404292,51234007,51504277,61573018);山东省自然科学基金项目(ZR2014EEQ010,ZR2015EL014);中央高校基本科研业务费专项(15CX05037A, 14CX06091A, 14CX05027A)
严侠(1989-),男,博士研究生,研究方向为非常规油气藏数值模拟。E-mail:jsyanxia1989@163.com。
黄朝琴(1981-),男,讲师,硕士生导师,研究方向为复杂介质渗流理论及油藏数值模拟。E-mail:emc.group.upc@gmail.com。
1673-5005(2016)03-0121-09doi:10.3969/j.issn.1673-5005.2016.03.016
TE 319; O 241.82
A
