CO2在原油中的扩散规律及变扩散系数计算方法

赵仁保, 敖文君, 肖爱国, 严　伟, 于志海,3, 夏晓婷

(1.中国石油大学油气资源与探测国家重点实验室,北京 102249; 2.中海油能源发展股份有限公司工程技术分公司,天津 300452; 3.中国石油集团渤海钻探工程有限公司,天津 300457)



CO2在原油中的扩散规律及变扩散系数计算方法

赵仁保1, 敖文君2, 肖爱国1, 严伟1, 于志海1,3, 夏晓婷1

(1.中国石油大学油气资源与探测国家重点实验室,北京 102249; 2.中海油能源发展股份有限公司工程技术分公司,天津 300452; 3.中国石油集团渤海钻探工程有限公司,天津 300457)

通过室内实验与理论计算相结合建立CO2在体相及多孔介质中变扩散系数的计算模型,得到不同黏度原油在多孔介质中的变扩散系数,并结合文献中的常扩散系数计算模型,利用MATLAB进行数据拟合与编程,对比分析两种计算方法下的平均扩散系数以及CO2在溶液中的传质扩散行为。结果表明:原油黏度越大,扩散系数越小,扩散平衡时间越长;采用变扩散系数可以更好地解释扩散过程中的非稳定阶段与稳定阶段,其扩散行为更符合实际条件下的扩散规律。

扩散系数; CO2; Fick定律; 传质

引用格式:赵仁保, 敖文君,肖爱国,等.CO2在原油中的扩散规律及变扩散系数计算方法[J].中国石油大学学报(自然科学版),2016,40(3):136-142.

ZHAO Renbao, AO Wenjun, XIAO Aiguo, et al. Diffusion law and measurement of variable diffusion coefficient of CO2in oil[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016,40(3):136-142.

CO2气体的大量释放是温室效应产生的主要因素,地质埋存可以有效减少大气中的CO2[1-5]。CO2主要以扩散的形式向液相中溶解,由菲克定律得到扩散通量J=-D·C,即扩散系数越大,扩散通量越大。扩散通量表示单位时间通过单位截面积的分子数量,而CO2在溶液中的溶解速率为单位时间溶解在一定体积液相中的分子数量,则CO2在溶液中的溶解速率随扩散系数的增加而增大。因此,当界面的面积一定时，CO2在溶液中的扩散系数决定了CO2在溶液中的溶解速率以及最终的溶解量。为了正确评价CO2埋存的长期安全性以及有效性,防止CO2气体从地层中泄漏,需要对CO2在地层水中的溶解及流动特性进行深入研究;另一方面,在CO2提高采收率过程中,分子扩散具有极其重要的作用。对于非混相驱,CO2在原油中的扩散速率决定了CO2吞吐过程中的焖井时间与周期,而核心参数之一为CO2在原油中的扩散系数;而对于混相驱,分子扩散行为直接影响黏性指进以及气体的突破时间[6-8],从而影响原油的最终采收率。针对气体扩散系数国内外学者从实验和数值模拟等方面进行了研究。由于在数值模拟过程中假设条件很多,而且初始和边界条件都与实际情况存在较大差异,其所得到的模拟结果很难具有说服性[9-12]。另外，在高压环境中进行实时的CO2浓度检测难度很大，一般通过间接的方法得到CO2扩散过程中的平均扩散系数,并进而表征CO2在溶液中浓度的变化,其结果与实际条件下的扩散现象会产生一定的差异。Riazi[13]提出压力衰竭法,通过测定扩散过程中PVT容器内气液界面的变化以及气相压力的衰竭行为，得到了CO2在稠油中的扩散系数。Zhang等[14]在Riazi研究的基础上对扩散模型进行修改,通过对扩散过程中压力数据进行拟合,得到了更简易的计算常扩散系数的方法。笔者在压力衰竭法基础上,结合Fick定律和气体状态方程得到CO2扩散过程中扩散系数与时间的变化关系式,即变扩散系数计算模型。通过对比分析,验证采用变扩散系数表征扩散过程的合理性。

1　实验方法

压力衰竭法的实验装置如图1所示。主要的实验设备有PVT容器、真空泵、高压气瓶以及压力传感器和温度传感器等。PVT容器半径1.72 cm,高度5.40 cm。由于气体体积以及气体在液相中的溶解度受温度影响变化大,整个扩散实验在恒温箱中进行,并实时监测温度的变化,减小扩散过程中温度的变化产生的实验误差。由于实验中最重要的数据是扩散过程中压力随时间的变化,所使用压力传感器的精度为0.01 kPa。CO2气体纯度为99.99%。

PVT容器内气相体积与填砂体积相等,保持恒定实验温度为299.15 K,气相初始压力为2 000 kPa,所用原油黏度分别为2.21、29.1和930.86 mPa·s，研究CO2在上述原油中的扩散实验，记录压力随时间的变化,并每30 s记录一次,如果3 h内压力的变化小于2 kPa,则认为CO2扩散已经达到平衡。

图1　扩散实验装置Fig.1　Apparatus of diffusion experiment

2　数值分析

压力衰竭法得到的常扩散系数代表的是CO2在整个压力衰竭过程的平均扩散系数,而当进行压力衰竭实验时,除了气相中的压力会随时间变化,液相内的CO2浓度也会随时间变化,这样整个压力衰竭扩散过程中这两种因素导致的扩散系数变化也会很大,因此如果以变扩散系数即扩散系数随时间和压力变化来表征整个扩散过程,则可以更好地反映扩散实际情况。

2.1常扩散系数的计算

常扩散系数计算采用Zhang等所得到的压力衰竭方法,扩散模型如图2所示。假设:①忽略扩散过程中液体的膨胀;②整个扩散过程温度恒定;③每个初始压力下,扩散系数为常量,不随压力和液相内浓度的改变而变化;④液相中只有气体的扩散,不发生流动;⑤忽略液相蒸发。

扩散方程为

(1)

由于忽略流动相,即v=0,方程式(1)只有扩散，则有

(2)

(3)

(4)

当方程式(4)中平衡压力产生微小变化时,图解法中的斜率变化很大,导致计算的扩散系数误差较大。为了减小平衡压力测定的误差,对压力衰竭曲线进行非线性回归拟合,得到了扩散过程中压力随时间变化的拟合方程以及常扩散系数表达式:

pt=a1exp(-b1t)+a2exp(-b2t)+c,

(5)

(6)

式中,a1,b1,a2,b2以及c为通过对压力衰竭曲线进行非线性回归拟合得到的常数。

2.2变扩散系数的计算

CO2扩散模型如图2所示,假设:①在整个扩散过程中,PVT容器内温度恒定,压力的变化只受CO2溶解扩散的影响;②液相体积恒定,即气液界面处位置始终恒定;③界面处浓度只受压力变化的影响;④初始压力假定为瞬间达到预设压力;⑤不考虑液相向气相扩散的量。

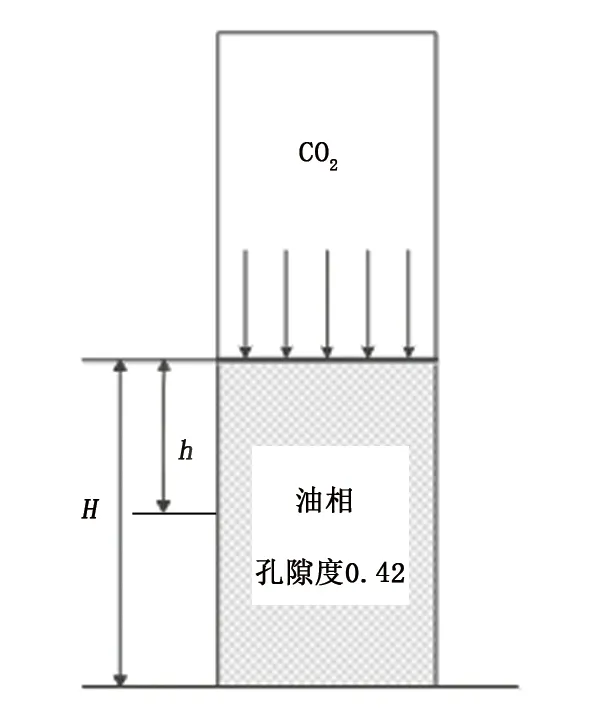
图2　CO2扩散模型示意图Fig.2　Schematic graph of diffusion model

对于封闭的PVT容器,由物质平衡原理可知,气相中减少的CO2量与液相中增加的CO2量相等。通过气体状态方程计算得到真实气体从初始状态(p0,t0)到某一时刻的状态(pt,ti)时气相中所减少的CO2量Δnt。

(7)

Z=Z(0)+ωZ(1).

(8)

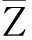
对于一维非稳态扩散方程(式(2)),其初始条件和边界条件有

h=0,t0

(9)

0

(10)

(11)

通过对扩散模型求解,可得到扩散过程中无因次浓度随时间和液相深度的变化:

(12)

C(t,h)表征的是从初始时刻到t时刻液相CO2浓度随时间的变化，对应于CO2在液相中的扩散系数Dt随时间的变化。

用Mt表示从初始时刻到t时刻气相中CO2扩散到液相中的累积量,M∞表示扩散平衡时,气相中CO2扩散到液相中的总量,则有

1)2π2t/4H2},

(13)

式(13)中的扩散时间间隔取极小值时,则有

(14)

由质量守恒定律可知,对于封闭的PVT容器装置,气相中减少的CO2量应与液相中增加的CO2量相等,即有Δnt=Mt。联立式(7)和(14)有

(15)

其中

(16)

式中,Δp∞为初始压力与平衡压力的差值。

方程(15)右部分取第一项可以得到扩散系数的近似表达式:

(17)

式(17)即为通过压力衰竭法所得到的CO2扩散过程中的变扩散系数,因为压力是时间的函数,则扩散系数也是时间的函数。通过压力衰竭过程中所得到的压力与时间的变换关系,可以求解得到扩散过程中不同时刻的扩散系数。

3　实验与计算结果分析

3.1常扩散系数

常扩散系数的计算基于式(5)和(6),通过PVT容器得到的扩散过程中压力随时间变化的数据,在压力衰竭方程(5)的基础上,利用MATLAB进行拟合,得到图3和数值计算结果(表1)。

图3　CO2-原油体系压力衰竭曲线和拟合曲线Fig.3　Pressure history and fitting curve of experiments

由图3看出,在3种不同黏度原油饱和的多孔介质中,压力曲线拟合均方差都大于0.99,表明拟合结果是有效的。从压力衰竭的过程可以看出,其整个扩散过程分为2个阶段,即扩散前期的压力快速下降阶段以及扩散后期的压力缓慢下降并趋于平缓阶段。扩散前期的压力快速下降阶段称为“潜伏期”[17]。这是因为在扩散的前期,气相初始压力较高,而溶液中CO2浓度为零,使得初始阶段CO2在溶液中快速扩散溶解。一定时间后,压力下降到一定程度,且溶液中已经有一定浓度CO2,这时候CO2在溶液中的溶解扩散速率逐渐缓慢,最后趋于平衡。

表1　CO2-原油体系压力衰竭实验与拟合结果

原油的黏度对CO2扩散行为有一定的影响,从表1看出,随着原油黏度的增加,CO2在原油中的平均扩散系数逐渐降低,扩散平衡时间逐渐增加,原油黏度的增加将降低CO2在原油中的扩散速率。同时,原油黏度越低,其扩散平衡压力也越低,由于实验在相同的初始压力下进行,平衡压力越低,则表明CO2在该原油中的溶解量越大，在原油中的溶解能力与原油的性质具有很大的关系。原油越稠,所含的轻质组分越少，胶质、沥青质等极性组分以及其他重组分含量增加,从而导致原油黏度越大,CO2在其中的溶解能力越差[18]。

3.2变扩散系数

变扩散系数计算的主要参数为扩散过程中压力的变化、初始压力、平衡压力和扩散时间。由于在多孔介质条件下CO2在液相中的扩散速率非常缓慢,在扩散实验过程中,并不是扩散完全达到平衡后停止实验,而是在扩散过程中当3 h内压力衰竭量小于2 kPa后停止实验,因此为了获得更多的实验数据,在变扩散系数的计算过程中,利用拟合方程得到更多的数据点。对于拟合得到的压力数据,当在1 h内压力衰竭量小于0.1 kPa时,即认为扩散已经达到平衡。通过扩散模型可以得到扩散过程中扩散系数随时间的变化关系曲线(图4)。

通过扩散系数的变化可以看出,整个扩散可以分为两个过程,即非稳态与稳态过程,与压力衰竭过程中的两个阶段一致。在这个过程中,扩散系数初始阶段上升很快,达到峰值后,又缓慢降低直到趋于稳定,产生这种变化的主要原因是,在扩散系数达到峰值之前的阶段,液相中靠近气液界面处CO2浓度瞬间达到平衡,而液相内部的CO2浓度为零,这样整个液相从上到下浓度不一样,从而导致了溶液内部密度差异,使得初始阶段CO2扩散由“浓度驱动”变为“浓度+密度驱动”，加快了CO2在液相中的扩散速率[19-24]。扩散一定时间后,一方面气相中压力降低了,另一方面CO2已分布在液相的整个区域中,溶液内的密度差异很小,达不到密度驱动而引起的自然对流的临界条件,此时的扩散为浓度差导致的扩散,所以扩散系数较小。随着扩散时间的增加,扩散系数逐渐降低,直到趋于稳定。同时,对比不同黏度时扩散的非平衡阶段发现,原油黏度越低,密度驱自然对流影响越明显,这是因为原油黏度越小CO2扩散速率越快,导致的密度差异就越大,对流影响就越大。

图4　多孔介质中CO2-原油体系扩散系数与时间的关系Fig.4　Diffusion coefficient of CO2-oil system in porous media

将从扩散实验开始到扩散稳定所得到的扩散系数取平均值,可以得到原油黏度为2.21、29.1和930.86 mPa·s时,其平均扩散系数分别为4.51×10-9、3.15×10-9和2.72×10-9m2·s-1,其平均值与用Zhang等[14]提出的平均扩散系数计算方法得到的值很接近(表1);同时,由于扩散系数的变化过程与实验测得的压力衰竭变化过程相对应,这两方面共同证明了变扩散系数计算模型的可靠性,所计算的扩散系数更符合实际的扩散行为。

3.3不同扩散系数下的扩散行为对比

用黏度为2.21 mPa·s的原油饱和多孔介质，研究在CO2在孔隙中的扩散行为,对比分析传质速率、累积扩散质量的差异。

将方程(14)进行转换可以得到扩散过程中累积扩散质量表达式:

(18)

方程右边第二项表示误差函数,其对累积质量影响不大,简化后有

(19)

扩散系数为常数时的累积扩散量表达式由Clark推导得到[25]:

(20)

图5　不同扩散系数下的累积CO2扩散量曲线Fig.5　Cumulative amount of CO2 diffusion with different diffusion coefficients

图6　不同扩散系数下,不同时刻传质速率曲线Fig.6　Mass transfer rate of with different diffusion coefficients

图5和图6分别为不同扩散系数时压力衰竭过程中的累积扩散量与传质速率关系,从图(6)看出,扩散过程存在很明显的两个阶段:非平衡与平衡阶段。结合传质速率曲线图,在非平衡阶段即扩散的前期,扩散系数为变量时的传质速率要高于扩散系数为常量时的传质速率,这主要是因为扩散初期的密度驱自然对流加快了CO2在液相中的溶解速率。在扩散的后期,在实际条件下液相内部的CO2浓度已经增加到一定的水平,此阶段的扩散速率应该变缓,这种现象与变扩散系数的计算结果一致。同时通过图5中CO2累积扩散量可以看出,两种扩散系数计算方法下,扩散过程中的累积扩散量差异较大,采用变扩散系数计算时,其扩散行为与实际扩散结果更接近，即初始扩散速率较快,扩散后期原油中累积的CO2逐渐趋于平衡。在实际的地质埋存以及CO2驱提高采收率过程中,只有获取到准确的累积扩散量才能准确确定扩散的前缘位置,因此,通过上面两图的对比分析,采用变扩散系数能更好地反映扩散过程的实际情况。

4　结　论

(1)相同初始压力下,原油黏度越大,CO2在原油中平均扩散系数越小,扩散平衡所需的时间越长。

(2)通过变扩散系数与时间的关系可以很好地解释扩散过程中存在的非稳定与稳定两个阶段。

(3)采用变扩散系数时,其传质行为更符合实际扩散过程,变扩散系数可以很好地解释密度驱动引起的自然对流对扩散行为的影响。

[1]GENTZIS T. Subsurface sequestration of carbon dioxide: an overview from an Alberta (Canada) perspective[J]. Int J Coal Geol, 2000,43(2):287-305.

[2]KLARA S M, SRIVASTAVA R D, MCILVRIED H G. Integrated collaborative technology development program for CO2sequestration in geologic formations United States Department of Energy R & D[J].Energy Convers Manage, 2003,44(17):2699-2712.

[3]赵仁保,孙海涛,吴亚生,等.二氧化碳埋存对地层岩石影响的室内研究[J]. 中国科学(技术科学),2010,40(4):378-384.

ZHAO Renbao, SUN Haitao, WU Yasheng, et al. Laboratory study on the effect of carbon dioxide buried on formation rock[J]. Sci China:Tech Sci, 2010,40(4):378-384.

[4]BENTHAM M, KIRBY G. CO2storage in saline aquifers[J]. Oil & Gas Science and Technology, 2005,60(3):559-567.

[5]任韶然,张莉,张亮. CO2地质埋存:国外示范工程及其对中国的启示[J]. 中国石油大学学报(自然科学版),2010,34(1):93-98.

REN Shaoran, ZHANG Li, ZHANG Liang. Geological storage of CO2: overseas demonstration projects and its implications to China[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010,34(1):93-98.

[6]敖文君,赵仁保,杨晓盈,等. 轻质油藏注富气驱提高采收率室内研究[J]. 石油天然气学报,2014,36(9):163-166,170.

AO Wenjun, ZHAO Renbao, YANG Xiaoying, et al. Laboratory study on enhanced oil recovery by enriched-gas flooding in light oil reservoirs [J]. Journal of Oil and Gas Technology, 2014,36(9):163-166, 170.

[7]杨胜来,杭达震,孙蓉,等. CO2对原油的抽提及其对原油黏度的影响[J]. 中国石油大学学报(自然科学版),2009,33(4):85-88.

YANG Shenglai, HANG Dazhen, SUN Rong,et al. CO2extraction for crude oil and its effect on crude oil viscosity[J].Journal of China University of Petroleum (Editon of Natural Science), 2009,33(4):85-88.

[8]苏玉亮,吴晓东,侯艳红,等.低渗透油藏CO2混相驱油机制及影响因素[J]. 中国石油大学学报(自然科学版), 2011,35(3):99-102.

SU Yuliang, WU Xiaodong, HOU Yanhong, et al. Mechanism of CO2miscible displacement in low permeability reservoir and influencing factor[J]. Journal of China University of Petroleum (Editon of Natural Science), 2011,35(3):99-102.

[9]PAU G S H, BELL J B, PRUESS K, et al. High-resolutionsimulation and characterization of density-driven flow in CO2storage in saline aquifers[J]. Advances in Water Resources, 2010,33(4):443-455.

[10]SONG L, KANTZAS A, BRYAN J L. Experimental measurement of diffusion coefficient of CO2in heavy oil using X-ray computed-assisted tomography under reservoir conditions[R]. SPE 137545,2010.[11]SOROUSH M, WESSEL-BERG D, TORSAETER O, et al. Affecting parameters intensity driven convection mixing in CO2storage in Brine[R]. SPE 154901,2012.

[12]PRUESS K, ZHANG K. Numerical modeling studies of the dissolution-diffusion-convection process during CO2storage in saline aquifers[C]//Technical Report LBNL-1243E, Lawrence Berkeley National Laboratory, California, 2008.

[13]RIAZI M R. A new method for experiment of diffusion coefficients in reservoir fluids[J]. J Pet Sci Eng, 1996,14(3/4):235-250.

[14]ZHANG Y P, HYNDMAN, MAINI B B. Measurement of gas diffusivity in heavy oils[J]. J Pet Sci Eng, 2000,25(2):37-47.

[15]CRANK J. The mathematics of diffusion[M]. Oxford: Second Clarendon Press,1995.

[16]LEE B I, KESLER M G. A generalized thermodynamic correlation based on three-parameter corresponding states[J]. AIChE J, 1975,21(3):510-527.

[17]RENNER T A. Measurement and correlation of diffusion coefficients for CO2and rich gas applications[J]. SPE Reserv Eng, 1988,3(2):517-523.

[18]李兆敏,陶磊,张凯,等. CO2在超稠油中的溶解特性实验[J]. 中国石油大学学报(自然科学版),2008,32(5):92-96.

LI Zhaomin, TAO Lei, ZHANG Kai, et al. Experiment on CO2dissolubility in ultra-heavy oil[J]. Journal of China University of Petroleum (Edition of Natural Science), 2008,32(5):92-96.

[19]LINDEBERG E, WESSEL-BERG D. Vertical convection in an aquifer column under a gas cap of CO2[J]. Energy Convers Manage, 1997, 38(sup 1):229-234.

[20]ENNIS-KING J P, PATERSON L. Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations[J]. SPE J, 2005,10(3):349-356.

[21]YANG C D, GU Y A. Accelerated mass transfer of CO2in reservoir brine due to density-driven natural convection at high pressures and elevated temperatures[J]. Ind Eng Chem Res, 2006,45(8):2430-2436.

[22]RIAZ A, HESSE M, TCHELEPI H A. Onset of convection in a gravitationallyunstable diffusive boundary layer in porous media[J]. J Fluid Mech, 2006,548(1):87-111.

[23]ALLEN R, SUN S Y. Carbon dioxide sequestration: modeling the diffusive and convective transport under a CO2cap[R]. SPE 160881, 2012.

[24]YANG C D, GU Y A. A new method for measuring solvent diffusivity in heavy oil by dynamic pendant drop shape analysis (DPDSA) [J]. SPE J, 2006,11(1):48-57.

[25]CLARK M M. Transport modeling for environmental engineers and scientists[M]. 2 ed. New York: John Wiley & Sons, 2009.

(编辑刘为清)

Diffusion law and measurement of variable diffusion coefficient of CO2in oil

ZHAO Renbao1, AO Wenjun2, XIAO Aiguo1, YAN Wei1, YU Zhihai1,3, XIA Xiaoting1

(1.State Key Laboratory of Petroleum Resource & Prospecting, China University of Petroleum, Beijing 102249, China;2.EngineeringTechnologyCompanyofCNOOCEnergyTechnology&ServicesLimited,Tianjin3000452,China;3.CNPCBohaiDrillingEngineeringCompanyLimited,Tianjin3000457,China)

A mathematical model of variable diffusion coefficient of CO2which can be used in bulk and porous media was established through the experiment and theoretical calculation. The variable diffusion coefficients of CO2in oils with different viscosity were calculated with this developed model. In order to validate this model, a traditional model of constant diffusion coefficient was used to calculate the average diffusion coefficient. The calculations with MATLAB software for the two models to analyze the diffusion coefficients and diffusion behaviors were also compared. The results show that the greater the viscosity of crude oil, the smaller the diffusion coefficient and the longer the diffusion equilibrium time. Diffusion behaviors of real condition, which contains unstable and stable stages, can be explained by the variable diffusion coefficient model with better results.

diffusion coefficient; CO2; Fick law; mass-transfer

2015-11-23

国家重点基础研究发展计划(2015CB250904); 国家自然科学基金项目(51274217)

赵仁保(1971-)，男，副研究员，博士，硕士生导师，研究方向为油气田提高采收率及稠油火驱。E-mail:zhaorenbao@vip.sina.com。

1673-5005(2016)03-0136-07doi:10.3969/j.issn.1673-5005.2016.03.018

TE 357.11

A