三轴交流漏磁检测矩形缺陷信号特征分析

廖肖晓，周绍骑，白金春

(1.后勤工程学院 军事供油工程系，重庆　401311； 2. 61255部队, 山西 临汾　043000)



三轴交流漏磁检测矩形缺陷信号特征分析

廖肖晓1，周绍骑1，白金春2

(1.后勤工程学院 军事供油工程系，重庆401311； 2. 61255部队, 山西 临汾043000)

针对三轴交流漏磁检测信号与缺陷定量之间关系的问题，利用Ansoft Maxwell软件，采用控制变量的方法对矩形缺陷交流漏磁检测进行三维有限元仿真。结果表明：缺陷长度、宽度、深度和旋转角度的变化会引起不同的漏磁场信号，可以利用三轴漏磁信号特征对缺陷进行定量分析，其中环向磁通密度分量对复杂缺陷的定量分析有重要的意义。该结果验证了理论分析的正确性。

三轴;交流漏磁;缺陷;信号特征;有限元分析

管道系统被广泛应用于石油、化工以及城市水暖等领域中，是石油和天然气等物质输送的主要手段[1]。管道在运行的过程中，其外表面最容易出现划伤和裂纹等缺陷，一旦由于裂纹等缺陷造成管道的失效破坏，会严重影响油气输送的经济效应以及管路周围生态和人员的安全[2-3]。

交流漏磁检测是综合了直流漏磁检测和涡流检测的精确测量表面缺陷的新型电磁无损检测技术[4]，在国内外越来越多地被用于管道缺陷的检测。日本学者Yuji Gotoh和 Norio Takahashi[5-6]在2001—2004年做了大量的研究工作，指出交流漏磁检测可以检测到更多缺陷信息，并解决了当2个近距离缺陷的漏磁场相互干扰时如何进行定量缺陷深度的问题。在国内，经过康中尉、吴德会、宋凯等学者的不断探索和研究，交流漏磁检测虽然起步较晚但也有了很大的进步[7-9]。但是，在这些研究过程中无论是数值模拟还是实验都是基于二维有限元分析或是仅仅检测管道的径向漏磁信号，并没有全面研究和利用轴向以及环向漏磁信号，这样检测到的漏磁信号对于缺陷尺寸的识别会造成一定的困难。本文针对这一问题，根据漏磁场三维特性，增加漏磁场检测分量，提出三轴交流漏磁检测方法，利用三维有限元仿真软件，采用控制变量的方法对不同的矩形缺陷进行数值模拟，得到漏磁信号特征与缺陷特征之间的关系，从而可更好地定量检测缺陷[10]。

1　三轴交流漏磁检测原理

三轴交流漏磁检测原理(图1)以传统的交流漏磁检测原理为基础，当铁磁性材料被交流磁化器磁化后，若被测试件表面光滑没有缺陷且内部没有夹杂物，进入导体的磁力线将全部通过被测试件；若存在缺陷，会导致缺陷处及其附近的磁阻增加而使得缺陷附近的磁场发生畸变，磁力线发生弯曲。此时通过传感器对材料表面进行扫查，对漏磁场信号进行分析和处理就可得到缺陷的相关信息[11]。

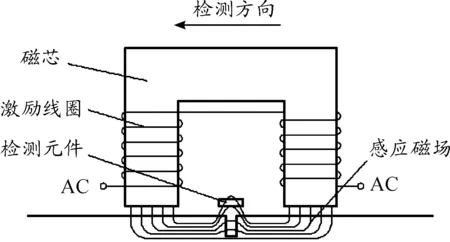
图1　三轴交流漏磁检测原理

三轴交流漏磁检测技术是将缺陷处形成的三维漏磁矢量场分为轴向、径向和环向分量，并在U型磁轨之间紧贴管壁处放置三相正交霍尔传感器，分别测量出缺陷漏磁场的轴向、径向和环向漏磁分量，可以更多地测量和记录缺陷的信息，提高管道表面缺陷的检测精度以及缺陷的识别能力[12]。

由于交流漏磁检测的趋肤效应，进入被测试件的磁化场受到涡流场的影响，进入被测试件的磁力线分布在其表面，因此更易于表面缺陷的检测。关于涡流的基本方程如下[6]：

(1)

(2)

式中：A为磁失势；μ为被检工件磁导率；J0感应涡流密度；φ为电场标量势；σ为电导率。

2　漏磁场仿真模型

本文采用Ansoft Maxwell 16.0对U型磁轨模型的磁化场进行三维建模分析。为简化模型，只取用了钢管的上半部分，由于磁化器较小，因此对结果没有影响，图2为漏磁模型的正视图和俯视图。

在模型中，线圈加载交流电流有效值I=0.8 A，磁轨左右两侧各缠绕的线圈匝数N=100，磁轨的相对磁导率为2 300，钢板为20号钢，钢管型号为φ159×5，常温情况下其相对磁导率为236，电导率为5.5 MS/m，励磁频率为1 000 Hz，加载Radiation Boundary辐射边界条件。网格划分情况见图3。

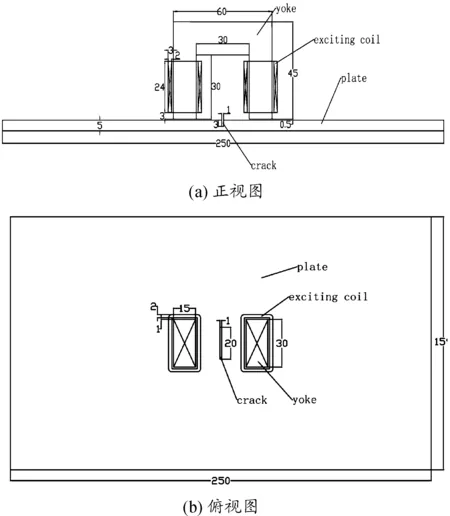
图2　漏磁模型

图3　网格划分情况

3　轴向长度改变对漏磁信号的影响

模型中的缺陷为横向缺陷，横向缺陷的环向长度、轴向长度和径向长度分别对应为模型中缺陷的长度(length)、宽度(width)和深度(depth)。为了研究缺陷宽度的改变对漏磁信号的影响，在标准缺陷长、宽、深度分别为20,1,3 mm 的基础上，保持长度和深度不变，改变宽度分别为0.5，1，1.5，2，2.5，3 mm。

在钢板上方d=0.5 mm处设置磁通密度查看路径。该路径是模拟探头的检测位置，设置为轴向方向，以缺陷中心作为路径的中点，路径长度L=16 mm。x=8 mm处为缺陷的中心位置。

图4为三相正交的霍尔元件检测到的磁感应强度分量，无论是轴向、径向还是环向都能检测到缺陷的存在，相对于传统的二维有限元仿真有着较为明显的优势。

环向分量Bx与轴向长度的关系如图4(a)所示，从中可以发现：环向分量Bx的波动范围随着轴向长度的增加而变大，虽然对轴向长度的界定有一定的帮助，但是其数值非常小，且很难发现其规律。

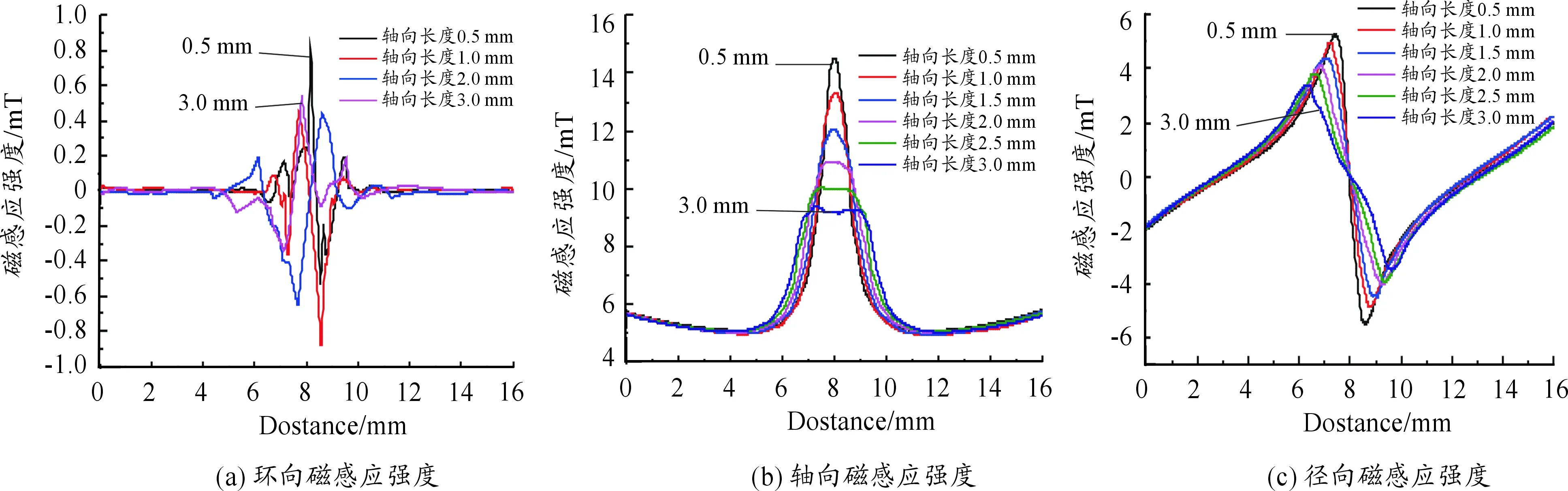
图4　磁感应强度

磁通密度轴向分量By随轴向长度变化的关系如图4(b)所示，可以看出：在轴向长度从0.5 mm递增到3.0 mm的过程中，轴向分量By是一个波峰形状，其幅值呈递减的趋势，当轴向长度增加到一定程度，其波峰已经变得非常缓和，甚至有变成2个波峰的趋势。

磁通密度径向分量Bz呈波峰波谷型，其幅值随着轴向长度的增加而减小，且波峰波谷的间距随着轴向长度的增加而增加，因此径向分量Bz对于缺陷轴向长度的界定有着重要的作用，可以作为缺陷轴向长度界定的特征值。其中，径向分量波峰波谷间距与缺陷轴向长度呈线性递增的趋势(图5)，其拟合优度高达0.997 2，可以作为轴向长度的界定方程：

y=0.823 8x+0.758 4， R2=0.997 2

(3)

式中：y为径向分量波峰波谷间距(mm)；x为缺陷轴向长度(mm)；R2为拟合优度。

4　径向长度改变对漏磁信号的影响

为研究缺陷径向长度的改变对漏磁信号的影响，在标准缺陷环向、轴向和径向长度分别为20，1，3 mm的基础上，保持环向和轴向长度不变，改变径向长度分别为1，1.5，2，2.5，3，3.5，4 mm。

在改变缺陷径向长度的过程中，由图6可以明显地看出：缺陷径向长度的改变只能引起磁通密度分量幅值的变化，轴向分量中波谷的位置以及径向分量中波峰波谷的相对位置都没有发生改变，这证明了改变缺陷径向长度不能引起磁通密度分量中波峰波谷相对位置的变化。

环向磁感应强度Bx同样与缺陷径向长度的改变没有明确的关系，因此没有做出其对应的关系图形。

由图6(a)可以看出：轴向分量By的幅值随着径向长度的递增呈增加的趋势，在1 mm递增到1.5 mm的过程中，幅值增加得比较快，在径向长度从1.5 mm增加到4 mm的过程中，幅值的增加幅度比较缓和，近似于指数函数的增加趋势，可以作为缺陷径向长度界定的特征值。数值拟合曲线如图7(a)所示，其拟合优度高达0.998 2，可以作为径向长度的界定方程，拟合方程为

(5)

式中：y为轴向分量幅值(mT)；x为缺陷径向长度(mm)。

磁通密度径向分量Bz与缺陷径向长度的关系如图6(b)所示，其幅值随着径向长度的增加呈幂函数递增的趋势，拟合优度达0.992 4。由于其幅值增加的速度比较小，分辨率比较低，可以作为缺陷径向长度的辅助界定方程。做出其数值拟合曲线，如图7(b)所示，其拟合方程为

y=1.896x0.849， R2=0.992 4

(6)

式中：y为径向分量幅值(mT)；x为缺陷径向长度(mm)。

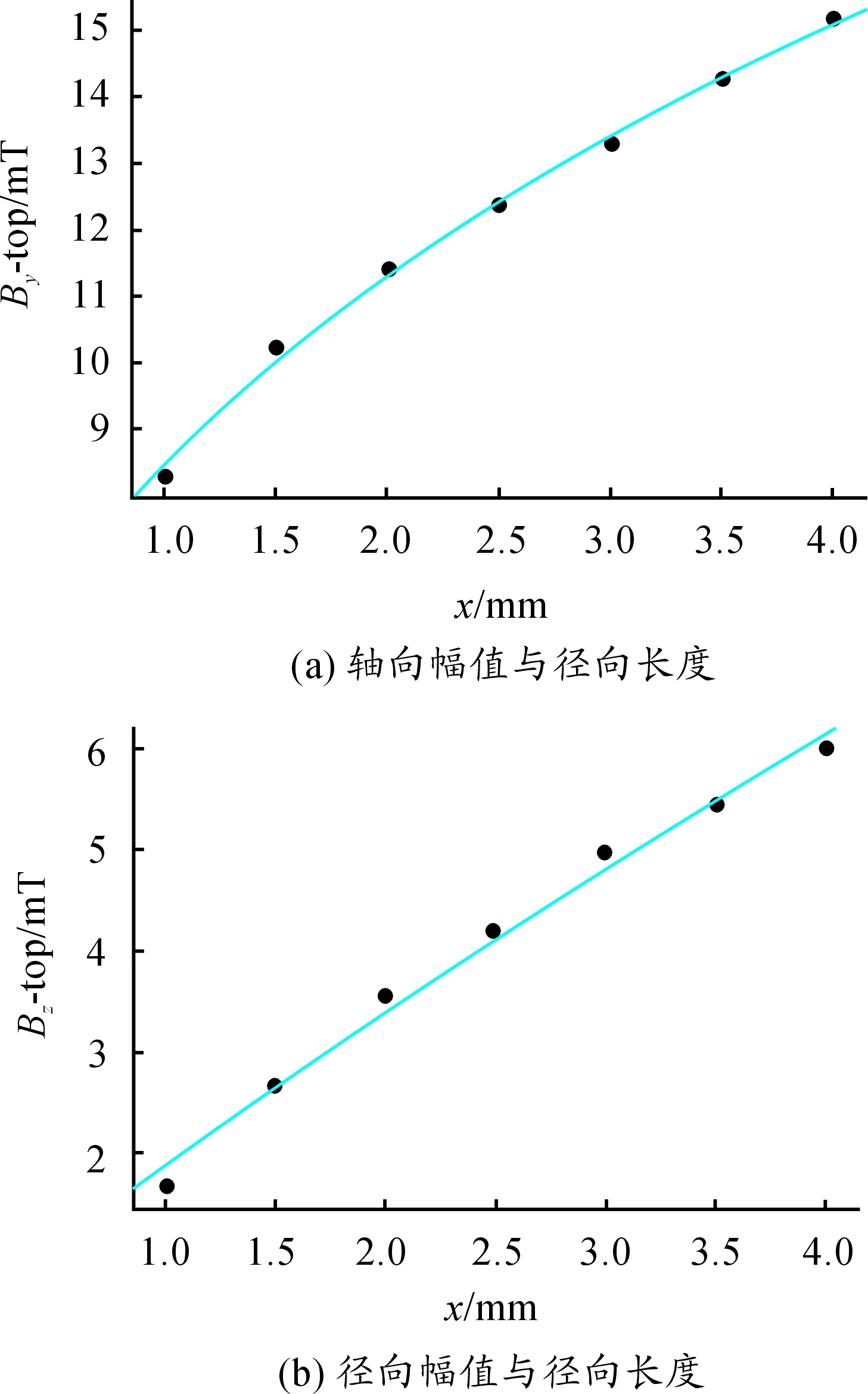
图7　深度拟合曲线

5　缺陷角度改变对漏磁信号的影响

改变矩形缺陷磁力线和缺陷的角度近似于管道上的复杂缺陷，在建立的模型中具体表现为缺陷的旋转，图8为磁力线在缺陷处的折射俯视图。改变缺陷旋转的角度，由0°～180°，从0°开始以15°的大小递增。

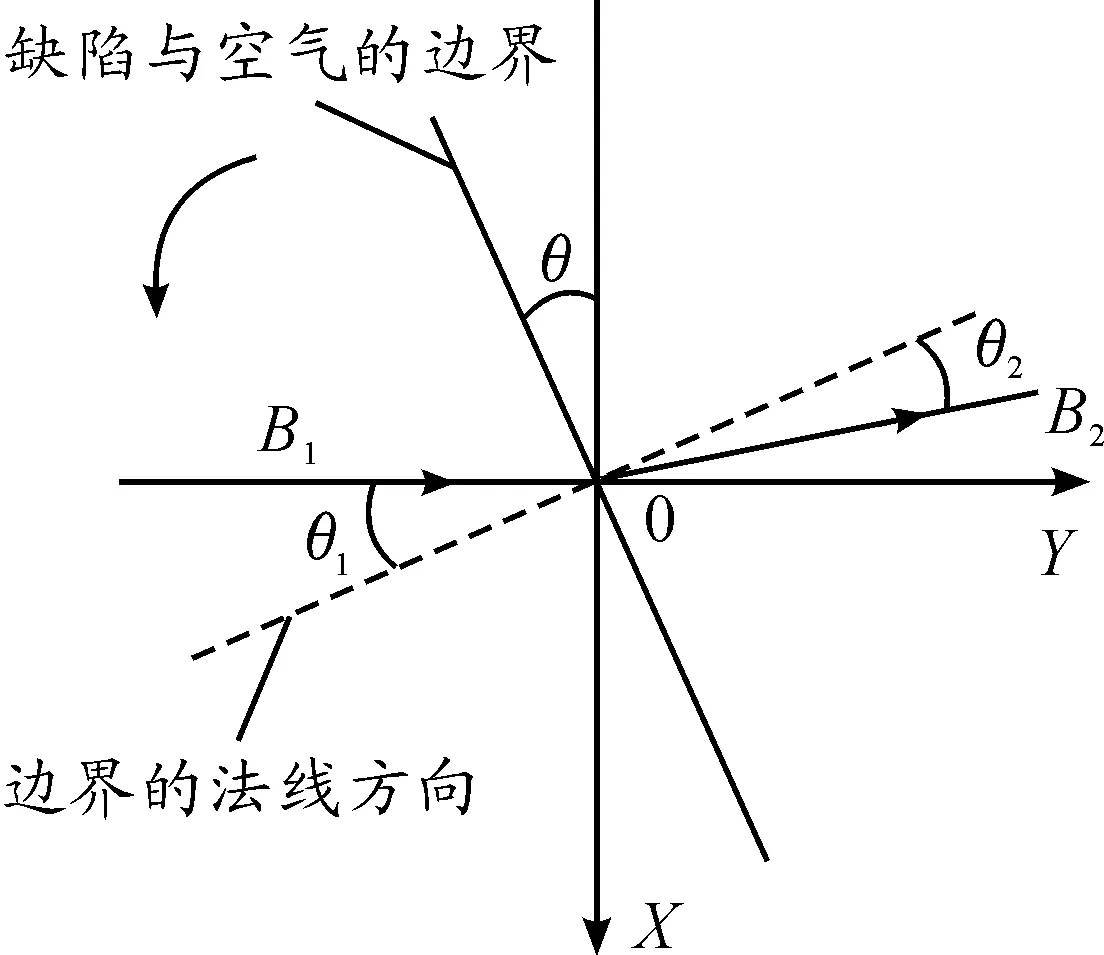
图8　磁力线在缺陷处的折射俯视图

当旋转角度为90°时，横向缺陷变为纵向缺陷，继续增加角度，纵向缺陷又变回横向缺陷，在这个变化过程中，根据不同介质分界面上的连续性边界条件[12]，当磁力线在缺陷处发生折射时，有如下公式：

(7)

(8)

从图8可以看出：若θ2>θ1=θ，那么折射后的磁力线与X正向成锐角，则环向磁通密度分量Bx为正值；若θ2<θ1=θ，折射后的磁力线与X正向成钝角，则Bx为负值。

图9中只取了环向和轴向的4个具有代表性的磁通密度分量与角度变化的曲线图，径向曲线图有着相同的规律，在这里不进行重复分析。通过磁通密度各分量的幅值与角度的关系可以得到其数据拟合曲线，见图10。由图10(a)可以看出：环向分量Bx幅值与角度近似于正弦函数关系，其拟合优度较高，R2=0.996 3，方程为

y=5.122sin(2.03x-1.015π)

(9)

式中：y为环向分量幅值(mT)；x为缺陷旋转角度值(°)。

图9　磁感应强度

轴向分量By的幅值与角度也近似于正弦函数关系，其拟合优度高达0.985 3。图10(b)为数据拟合曲线，方程为

y=9.635+4.404sin(1.934x+0.531π)

(10)

式中：y为轴向分量幅值(mT)；x为缺陷旋转角度值(°)。

考虑到x∈[0,π]，因此只需通过这2个方程就可以确定唯一的角度值。

同时可以发现：当缺陷由横向缺陷旋转为纵向缺陷时，传感器无法检测到漏磁场的变化，因此轴向励磁的方式无法检测出纵向缺陷的存在。通过仿真得到的结果与理论一致，证明了理论分析的正确性，也证明了磁通密度环向和轴向分量在界定复杂裂纹缺陷时有很重要的意义。

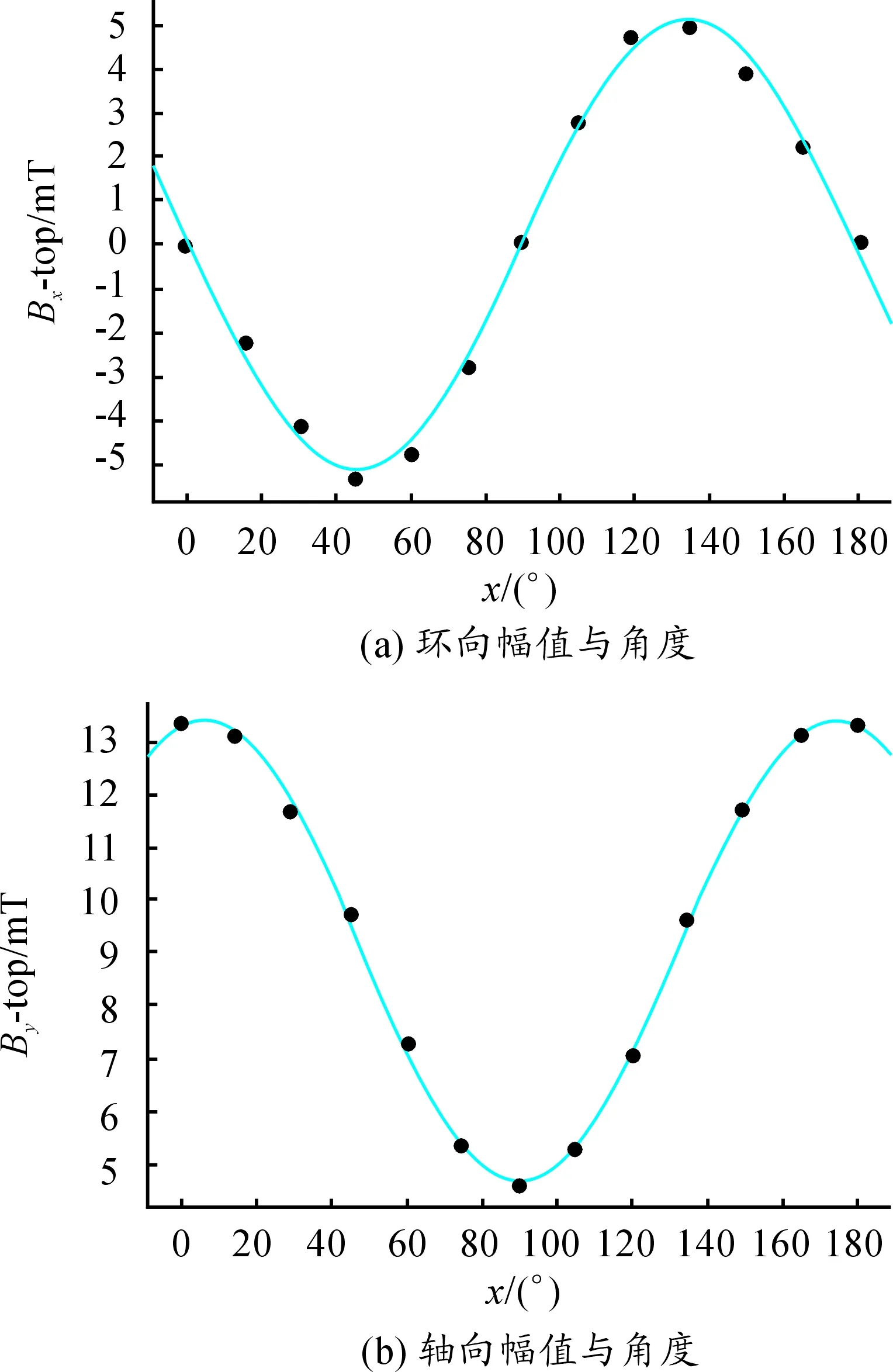
图10　角度拟合曲线

6　结论

三轴交流漏磁检测方法相对于传统的检测方法可以提高对缺陷的识别度，从而较多地记录缺陷的信息。针对矩形缺陷的漏磁场信号特征进行了三维有限元仿真，结果表明：

1) 只有缺陷宽度的改变可以引起径向分量波峰波谷位置的相对变化，因此由波峰波谷的相对位置可以界定缺陷的宽度。

2) 缺陷的深度与磁通密度的轴向分量幅值有着拟合优度极高的线性关系，配合径向分量幅值可以近似地界定缺陷的深度。

3) 缺陷长度与磁通密度的轴向和径向分量幅值的拟合优度很接近但都不是特别高，利用两者的搭配对于缺陷长度的界定有一定的帮助。

4) 环向磁通密度分量在横向缺陷检测中的作用不大，但随着缺陷旋转角度的增加，其磁通密度分量的幅值呈正弦函数的变化趋势，且拟合优度极高，因此环向磁通密度分量对复杂矩形缺陷的定量分析有很重要的意义。

本研究仅数值模拟了矩形缺陷的漏磁信号，下一步将扩充到更多的缺陷形式并建立各种缺陷的漏磁信号特征分类。

[1]康中尉,罗飞路,潘孟春,等.钢管表面缺陷检测用交变漏磁检测系统[J].无损检测,2006,28(4):189-191.

[2]张海燕,方晓艳,马小芳,等.管道三维漏磁检测的有限元仿真应用[J].仪表技术与传感器,2012 (11):163-165.

[3]宋志强,李著信,张镇,等.基于连续小波变换的输油管道裂纹缺陷漏磁检测研究[J].化工自动化及仪表,2010,37(7):35-39.

[4]丁劲锋,康宜华,刘德杰.钻具螺纹的交流漏磁法探伤[J].无损检测,2007,29(9):537-539.

[5]YUJIG，NORIOT.3-Dnonlinearanalysisofeffectofairgapbetweenyokeandsteelinalternatingfluxleakagetesting[J].IEEETransactionsonMagnetics,2001,38(2):1085-1088.

[6]YUJIG.NORIOT.Proposalofdetectingmethodofpluralcracksandtheirdepthbyalternatingfluxleakagetesting:3-Dnonlineareddycurrentanalysisandexperiment[J].IEEETransactionsonMagnetics,2004,40(2):655-658.

[7]康中尉.矩形缺陷的交变漏磁检测信号分析方法[J].无损检测,2006,28(11):565-568,586.

[8]吴德会,游德海,柳振凉,等.交流漏磁检测法趋肤深度的机理与实验研究[J].仪器仪表学报,2014,35(2):327-336.

[9]宋凯,陈超,康宜华,等.基于U形磁轭探头的交流漏磁检测法机理研究[J].仪器仪表学报,2012,33(9):1980-1985.

[10]杨理践,邢磊,高松巍.三轴漏磁缺陷检测技术[J].无损探伤,2013,37(1):9-12.

[11]奉华成,黄松岭,赵云利,等.三维漏磁检测实验平台的研制[J].电测与仪表,2011,48(544):27-29,57.

[12]姜福琨.管道漏磁三轴检测方法的理论研究[D].沈阳:沈阳工业大学,2014.

(责任编辑杨黎丽)

Signal Analysis of Tri-Axial AC-MFL Inspection for the Rectangular Defect

LIAO Xiao-xiao1，ZHOU Shao-qi1，BAI Jin-chun2

(1.Department of Petroleum Supply Engineering, Logistic Engineering University,Chongqing 401311, China; 2.The No. 61255thTroop of PLA, Linfen 043000, China)

For the problem of relationship between signal of tri-axial AC-MFL inspection and quantitative analysis of defects, a finite element of AC-MFL detection system was build by adopting Ansoft Maxwell program to simulate the 3-D static situation in the method of control variables. Results show that the change of defect length, width, depth and rotation angle will cause different magnetic field leakage signal. Three-axis magnetic flux leakage signal feature could be used for quantitative analysis of defects. In particular, it was shown that axial magnetic flux density had an important significance for quantitative analysis of complex defects. The results demonstrate the validity of the theoretical analysis.

tri-axial; AC-MFL; defect; signal characteristic; finite element analysis

2016-03-28

廖肖晓(1991—)，男，湖北谷城人，硕士研究生，主要从事无损检测技术研究，E-mail:312343912@qq.com。

format：LIAO Xiao-xiao，ZHOU Shao-qi，BAI Jin-chun.Signal Analysis of Tri-Axial AC-MFL Inspection for the Rectangular Defect[J].Journal of Chongqing University of Technology(Natural Science)，2016(9):106-112.

10.3969/j.issn.1674-8425(z).2016.09.017

TG115.28

A

1674-8425(2016)09-0106-07

引用格式：廖肖晓，周绍骑，白金春.三轴交流漏磁检测矩形缺陷信号特征分析[J].重庆理工大学学报(自然科学)，2016(9):106-112.