基于带谐重力场的测高卫星轨道设计

高　凡　彭碧波　钟　敏　许厚泽

1　中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077 2　中国科学院大学，北京市玉泉路甲19号，100049



基于带谐重力场的测高卫星轨道设计

高凡1,2彭碧波1钟敏1许厚泽1

1中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077 2中国科学院大学，北京市玉泉路甲19号，100049

推导了一组测高卫星轨道设计的理论公式，介绍了相关方法，并编写了一套软件。分别以激光测高卫星ICESat和雷达测高卫星HY-2A为例，基于31阶地球带谐重力场，给出了其平均轨道参数与密切轨道参数。轨道模拟显示，卫星经过各自的回归周期之后，其星下点均能精确回到初始位置，并且长半轴、轨道倾角、偏心率和近地点幅角均没有发生长期和长周期的变化，符合参考轨道要求。

测高卫星；重复地面轨迹；冻结轨道；HY-2A

卫星测高是一种先进的卫星大地测量手段，主要分为雷达测高和激光测高2种模式。在雷达模式下，其观测直径为1.2～6 km[1]，而对于激光模式，其地表光斑的直径仅为大约70 m[2]。它们的星下点需要按所设计的轨迹周期性运动，因此，严格重复地面轨迹轨道在测高卫星轨道设计中显得尤为重要。另外，为了维持该模式，卫星在轨运行中长半轴、偏心率、轨道倾角和近地点幅角这4个轨道根数不能发生长期与长周期的变化。

针对不同的卫星任务，国际上一些学者对此问题作了深入研究。1990年，美国宇航局(NASA)的Carl[3]针对GeoSat卫星的严格重复地面轨迹模式，基于地球重力场J2项，提出计算卫星轨道平均长半轴的方法。1995年，德克萨斯大学空间研究中心(CSR)的Samsung[4]基于31阶地球重力场，系统地对NASA地球科学部的激光测高卫星系统(GLAS)的轨道进行了设计、模拟与分析。1997年，西班牙萨拉戈萨大学的Antonio等[5]提出直接在地固系下求出周期运行轨道的方法。1999年，西班牙皇家天文台的Martin[6]在Antonio基础上，基于较高阶的带谐重力场给出了计算重复地面轨迹轨道模式下的方法。2008年，Martin[7]给出基于高阶重力场的一种快速设计重复地面轨迹轨道的方法，并对Topex/Poseidon卫星127圈/10 d模式下的轨道进行分析。 2008年，CSR的Nadege[8]对NASA的ICESat卫星在3种严密重复地面轨迹模式下的地面轨迹子周期、轨道机动以及交叉点进行了非常详细的描述与分析。以上工作主要是来自美国的NASA与法国的CNES[9]，其目的是在满足工程需求的同时，减少轨道机动次数，节省燃料，延长卫星寿命。我国第一颗测高卫星——HY-2A作为一颗试验卫星已经成功在轨运行[10,11]，鉴于我国未来还有更多的测高卫星任务[12-14]，积极开展此类卫星的轨道设计研究具有较大的工程价值。

本文首先依据重复地面轨迹轨道与冻结轨道的特征，利用拉格朗日行星方程分析平均带谐重力场对各轨道根数的摄动，优化平均轨道元素确定的公式，使之便于程序计算。然后，分别对短周期项中的一阶项与余项进行修正，并以ICESat与HY-2A为例给出31阶带谐重力场下符合条件的平均轨道元素和密切轨道元素。

1　重复地面轨迹轨道与冻结轨道的特征

所谓重复地面轨迹轨道是指：在惯性系下，卫星围绕地球运动了N圈，在地固系下，卫星的升交点轴(不连续的)旋转了D圈之后，两者正好重复通过地球上固定的同一子午面，其中N和D是两个互质的正整数。

为了使轨道维持上述重复地面轨迹轨道模式，要求卫星在轨运行中，其长半轴、偏心率、轨道倾角和近地点幅角均不产生长期和长周期的变化。

2　平均轨道根数的确定

卫星在轨运行时，重力场是最主要的摄动源，其对轨道根数的摄动分为长期项、长周期项和短周期项[12-13]。只考虑长期项和长周期项影响而得到的轨道根数，称为平均轨道根数。本节首先介绍分离长期项和长周期项的方法，并推导出经正则化的平均带谐重力场表达式，以便于程序计算。其次，利用拉格朗日行星方程，给出平均带谐重力场对各个轨道根数摄动的表达式。最后，提出一种较为简洁的确定平均长半轴的方法，并介绍确定平均偏心率的方法。

2.1平均带谐重力场对各轨道根数的摄动分析

平均带谐重力场的表达式如下：

(1)

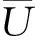
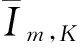
将式(1)代入拉格朗日行星方程[15]可得：

(2)

(3)

(4)

(5)

(6)

(7)

2.2平均轨道根数的确定

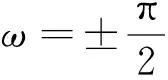
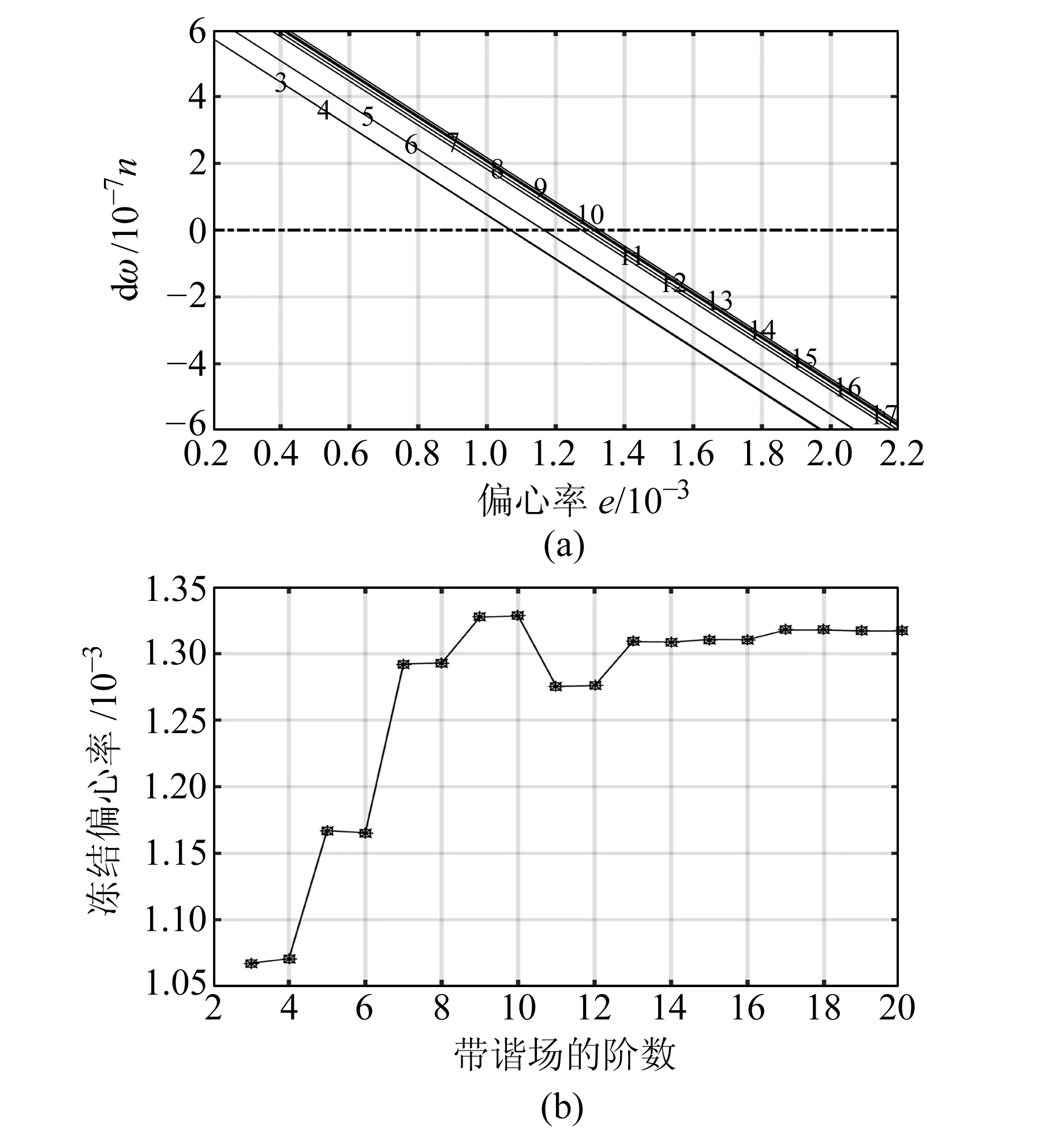
图1　冻结偏心率的确定(a=6 971 519.180,i=94)Fig.1　The determination of frozen eccentricity (a=6 971 519.180,i=94)

根据重复地面轨迹轨道的特性有：

(8)

(9)

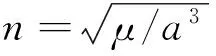
(10)

式(10)两边都包含有a，其初值取：

(11)

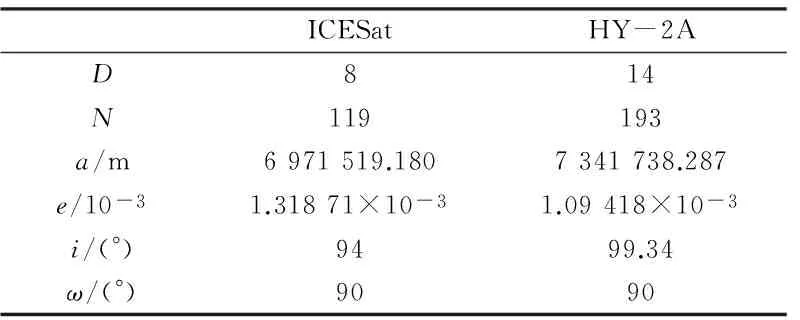
表1　ICESat和HY-2A的平均轨道根数

表中的D、N和i等相关信息来自文献[2]和文献[17]。

3　密切轨道根数的确定

§2.2中得到的平均轨道根数，需要经过短周期项修正转化成密切轨道元素，才能产生实际应用价值。本节将介绍修正短周期项的方法。

3.1修正短周期摄动项中一阶项的影响

密切轨道根数与平均轨道根数的关系如下：

(12)

(13)

利用拉格朗日行星方程，可以求出q*中的各个分量[4]。

表2给出了ICESat经一阶短周期项改正的初始轨道和由该初始轨道在31×0的GGM03带谐重力场下经8阶Guass-Jackson积分器积分[18]得到的最终轨道。

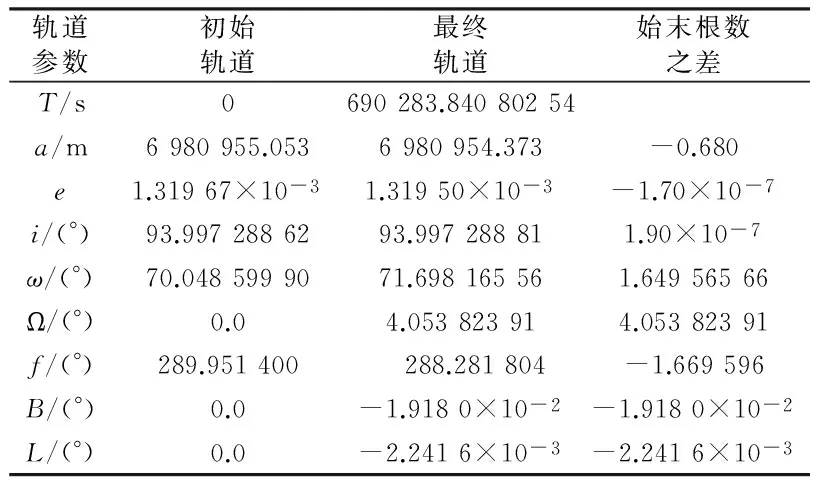
表2　ICESat的平均轨道根数+短周期项一阶项

表2中的B和L分别表示卫星的大地纬度与大地经度。从这两项可以看出，加上一阶短周期摄动项之后，地面轨迹并不能闭合，在地面上纬度方向和经度方向分别会产生大约-122 332 m 和-14 297 m的距离之差。

3.2修正其他短周期项的影响

从表2可以看出，始末轨道根数之间的差别主要是在近地点幅角ω与真近点角f 上。为了消除这一差别，需要继续调整初始轨道元素，使之满足下列方程：

(14)

(15)

式中,ω(q0,tf)、f(q0,tf)是在31×0 GGM03带谐重力场下由8阶Gauss-Jackson 积分器得出，ω0为初始的近地点幅角，f0为初始的真近点角。对于式(14)和式(15)，只有两个方程但是有7个未知数，在此只选择调整a和e，那么有：

f(a0,e0,tf)-f0=0

式中，a 的单位取地球赤道平均半径为1。

(16)

式中，δa0、δe0可分别取值为1 m与1×10-6，ff为f(a0,e0,tf)，ωf为ω(a0,e0,tf)，式(16)中偏导数的计算方法参见文献[4]。

表3显示，两颗卫星经过特定时间都能精确地回到初始位置，并且初始轨道根数与最终轨道根数之差很小。

图2～5分别给出了HY-2A在193圈/14 d模式下，采样率为60 s时密切轨道根数中的长半轴、轨道倾角、偏心率和近地点幅角随时间变化的情况，白线为其平均轨道元素值。图2、图3显示长半轴和轨道倾角都在其平均轨道根数附近小范围均匀变化，图4、图5显示偏心率和近地点幅角都集中在其平均轨道元素附近变化。以上结果表明，图中各个轨道根数均没有产生长期和长周期的变化，符合冻结轨道要求。

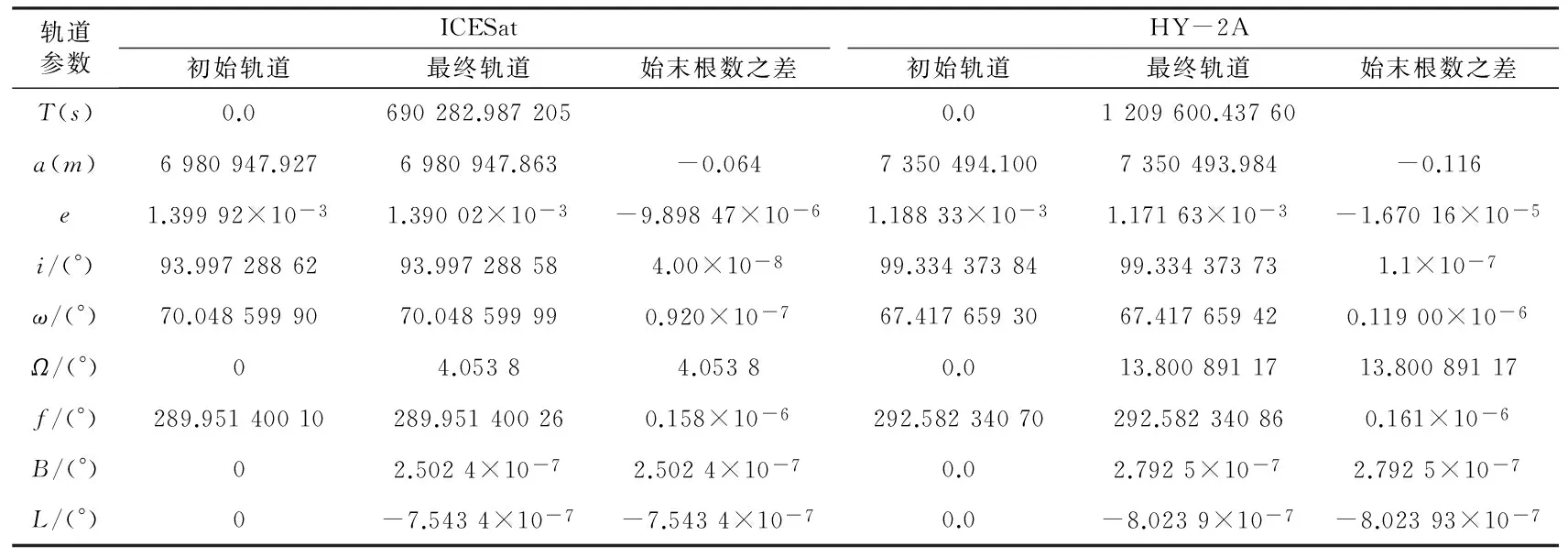
表3　ICESat与HY-2A的密切轨道元素

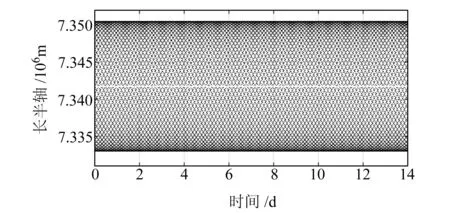
图2　长半轴随时间变化情况Fig.2　Semi-major history of HY-2A

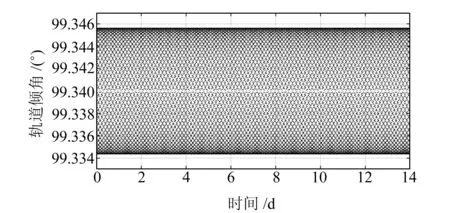
图3　轨道倾角随时间变化情况Fig.3　Inclination history of HY-2A

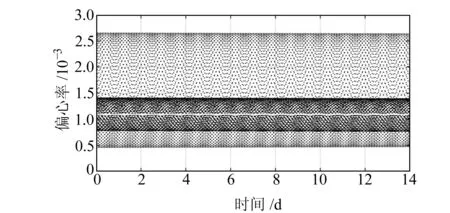
图4　偏心率随时间变化情况Fig.4　Eccentricity history of HY-2A

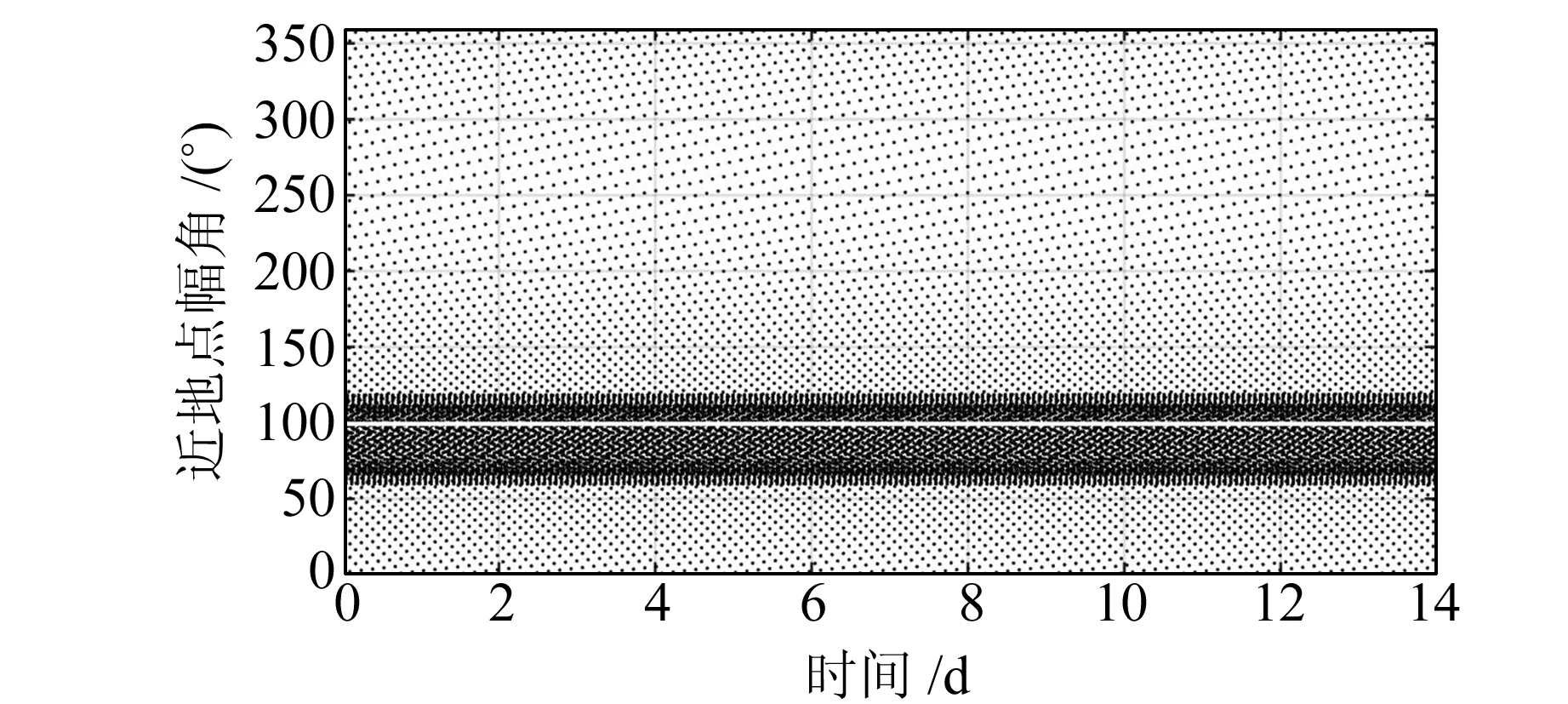
图5　近地点幅角随时间变化情况Fig.5　Argument of perigee history of HY-2A

4　结　语

测高卫星的轨道设计需要满足两个条件：严密重复地面轨迹轨道和冻结轨道。围绕这个问题，本文系统介绍了基于带谐重力场的测高卫星轨道设计的方法与步骤，并以激光测高卫星ICESat和雷达测高卫星HY-2A为例对各个步骤作详细说明。

本文主要完成了以下工作：1)推导出经正则化的平均带谐重力场表达式，并利用拉格朗日行星方程，给出平均带谐重力场对各个轨道根数摄动的表达式；2)介绍了确定平均偏心率的方法，并提出一种能满足重复地面轨迹轨道的条件和确定平均长半轴的简洁方法；3)介绍了修正短周期项摄动的方法，并确定了密切轨道参数；4)在GGM03中的带谐重力场下，利用Gauss-Jackson积分器，通过轨道模拟验证了所求得密切轨道符合严密重复地面轨迹轨道和冻结轨道的要求。结果表明，本文的算法以及自主编写的软件精确可靠，具有一定的理论价值和较大的工程应用价值。

下一步的工作是将更多的摄动因素纳入到轨道设计的范围，如田谐重力场、日月引力、大气阻力和太阳光压等，以及针对未来的卫星任务，积极开展更为细致的工作，如对更长回归周期的轨道进行设计，对其地面轨迹的子周期进行分析等。

[1]Seeber G.Satellite Geodesy: Foundations, Methods, and Applications [M].Berlin: Walter de Gruyter,2003

[2]Waleed A, Zwally H J,Rorbit B, et al.The ICESat-2 Laser Altimetry Mission[J]. Proceedings of the IEEE,2010,98(5):735-751

[3]Carl A W.A Prograde Geosat Exact Repeat Mission?[J].Journal of the Astronautical Sciences, 1991,39(1):313-326

[4]Samsung L.Orbit Analysis and Maneuver Design for the Geoscience Laser Altimeter System [D]. Austin: The University of Texas, 1995

[5]Antonio E, Martine L.Frozen Orbits in the Tesseral Artificial Satellite Theory[C]. The 12th International Symposium on Space Flight Dynamics,1997

[6]Martin L.Searching for Repeating Ground Track Orbits: A Systematic Approach [J].The Journal of the Astronautical Sciences,1999,47(3):177-188

[7]Martin L, Ryan P R.Fast Design of Repeat Ground Track Orbits in High-fidelity Geopotentials[J]. The Journal of the Astronautical Sciences, 2008, 56(3):311-324.

[8]Nadege P.Mission Design Concepts for Repeat Groundtrack Orbits and Application to the ICESat Mission[D]. Austin: The University of Texas,2008

[9]Martin L.SADSaM: A Software Assistant for Designing Satellite Missions[R].CNES Report No. DTS/MPI/MS/MN/99-053,1999

[10]张庆君, 张健, 张欢,等. 海洋二号卫星工程研制及在轨运行简介[J]. 中国工程科学, 2013(7):12-18(Zhang Qingjun,Zhang Jian,Zhang Huan, et al. The Study of HY-2A Satellite Engineering Development and In-orbit Movement [J]. Engineering Sciences, 2013(7): 12-18)

[11]Gao F,Peng B B,Zhang Y, et al. Analysis of HY-2A Precise Orbit Determination Using DORIS[J]. Journal of Advances in Space Research,2015,55(5):1 394-1 404

[12]Bao L F, Xu H Z, Li Z C. Towards A 1 mGal Accuracy and 1 min Resolution Altimetry Gravity Field [J]. Journal of Geodesy,2013, 87: 961-969

[13]鲍李峰, 许厚泽. 双星伴飞卫星测高模式及其轨道设计[J]. 测绘学报, 2014,43 (7): 661-667(Bao Lifeng, Xu Houze.Twin-Satellites Altimetry Mode and Its Orbit Design[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43 (7): 661-667)

[14]李洋,张润宁. 高度计测距精度对沿轨迹重力异常反演的影响[J]. 测绘学报，2015, 44(4): 363-369(Li Yang, Zhang Running．Inference of Altimeter Accuracy on Along-Track Gravity Anomaly Recovery[J]. Acta Geodaetica et Cartographica Sinica,2015, 44(4): 363-369)

[15]Escobal P R. Methods of Orbit Determination [M].Florida: Krieger Publishdhing Company, 1975.

[16]Tapley B, Ries J, Bettadpur S, et al. The GGM03 Mean Earth Gravity Model from GRACE[C]. AGU Fall Meet, 2007

[17]Zhang Y, Vincent T. Input Data for HY-2 Precise Orbit Determination[R]. NAOAS and CNES,2011

[18]Matthew M B, Liam M H. Implementation of Gauss-Jackson Integration for Orbit Propagation[J]. Journal of the Astronautical Sciences, 2004,52(3):331-357

About the first author:GAO Fan, PhD candidate,majors in orbit design and precise orbit determination, E-mail: gaofan02006@126.com.

Altimetry Satellite Orbit Design Based on Zonal Geopotential

GAOFan1,2PENGBibo1ZHONGMin1XUHouze1

1State Key Laboratory of Geodesy and Earth’s Dynamics, Institute of Geodesy and Geophysics, CAS,340 Xudong Street, Wuhan 430077,China 2University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049,China

The orbits of altimetry satellites should be repeat groundtrack and frozen. We derive an algorithm of the orbit design based on zonal geopotential field and develop the software by ourselves. This paper takes ICESat and HY-2A as examples, computing their mean orbit elements and osculation orbit elements. The orbit generation results show that the satellites can get a nice closure after a full cycle and there is no secular and long period change for the semi-major, eccentricity, inclination and the argument of perigee. The orbit can meet the requirement of altimetry satellites and can be taken as a reference orbit.

altimetry satellite; repeat groundtrack; frozen orbit; HY-2A

National Natural Science Foundation of China, No. 41131067.

2015-09-30

高凡，博士生，主要从事卫星轨道设计与精密定轨研究，E-mail: gaofan02006@126.com。

10.14075/j.jgg.2016.10.004

1671-5942(2016)010-0859-05

P228

A

项目来源：国家自然科学基金(41131067)。