坐标转换求解算法分析与研究*
2016-10-27杨德宏
李 勇,杨德宏
(1.大理州国土资源规划研究院,云南 大理 671000; 2.昆明理工大学 国土资源工程学院,云南 昆明 650093)
坐标转换求解算法分析与研究*
李勇1,杨德宏2
(1.大理州国土资源规划研究院,云南 大理671000; 2.昆明理工大学 国土资源工程学院,云南 昆明650093)
在大地测量或工程测量实践中,不可避免的需要解决测量坐标系统建立及坐标转换的问题。文章以布尔沙转换模型为基础,对坐标转换的5种求解算法进行分析,并以某工程为例,采用MATLAB软件编程进行计算比对分析,结果表明:坐标重心化算法求解转换参数和转换坐标,其结果出现异常,计算结果和理论分析发现,该算法不适合布尔沙转换模型,而其余4种算法求出的坐标转换参数和坐标转换结果相当,能保证精度,具有可靠性。
布尔沙模型;坐标转换算法;对比分析
0 引言
实施坐标转换,如果已知转换参数,那么应用转换公式直接进行坐标转换计算即可,但实际面临的情况往往是转换参数未知,为此需要使用公共点求解转换参数,且一般都有多余方程,为得到唯一解,在满足最小二乘原则的基本前提下有最小二乘算法、坐标重心化算法、基于尺度因子算法、最小二乘分解算法等扩展算法。本文以布尔沙模型为基础,以某工程为例,分析不同算法的适宜性和解算精度。
1 布尔沙模型
布尔沙模型计算公式如下:
2 衡量坐标转换精度指标
重合点残差:
V=重合点转换坐标值-重合点已知坐标值
(2)
空间点位中误差:
(3)
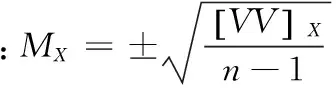
3 几种坐标转换求解算法分析
3.1传统最小二乘算法
以重合点的原坐标系坐标和目标坐标系坐标为观测值,建立误差方程,按VTPV=min的原则组成法方程,进而求逆解算法方程得到作为未知数的转换参数。
3.2最小二乘分解法
用传统最小二乘算法,需要对7阶矩阵求逆,坐标转换中坐标数据量较大,可能出现求逆的数值不稳定。为此,可采用最小二乘分解算法,其基本思想是把布尔沙7参数法模型作线性表达[2]:
AS=B
(4)
S=[ΔxΔyΔzkεxεyεz]T;
B=[XTYTZT]T。
把系数矩阵A分解为以下形式:
A=QR
(5)
式中:Q为N×7列的正交矩阵;R为7×7阶的上三角矩阵。式(4)表达为:
RS=QTB
(6)
运用以上方法求解坐标转换参数过程中不需要对矩阵求逆也可得到坐标转换参数S的最小二乘解。
3.3坐标重心化求解算法
工程实际应用中,重合坐标点在局部区域,可能仅分布在空间直角坐标系中的某一象限,并不是均匀的分布在空间直角坐标系中,其转换过程中会影响布尔沙7参数的精度,增加转换模型的误差。为此,提出原点坐标重心化算法。该方法是先将两个坐标系的原点平移至公共点的重心位置,重新建立空间直角坐标,使坐标点在新坐标系中均匀分布,进而得到7参数,得到过渡的布尔沙模型,解算出重心化坐标系中的坐标,然后再平移换算到相应坐标系中[3]。
3.4基于尺度因子求解算法
坐标转换模型本身是一个非线性函数,通常是将非线性转化为线性后求解,这种线性处理增加旋转矩阵中各项旋转参数的误差。针对尺度因子,从两个空间直角坐标系中同一线段的长度比出发,通过多个公共点组成的多条公共线段,首先通过条件平差,得出具有高精度的尺度因子m,然后将尺度因子m作为已知值代入7参数转换模型中,变成含有6参数的转换模型,通过公共点以及最小二乘配置法得出剩余6参数[4]。
3.5总体最小二乘算法
在高斯-马尔科夫模型中采用最小二乘配置法对其误差方程进行求解过程中,首先假设观测向量L中含有偶然误差,而其系数矩阵A中是不含有偶然误差的。如果系数矩阵A中存在偶然误差或者扰动时,基于统计学观点看来,基于最小二乘配置法求出的估值将不再是最优解,是存有偏差的。最小二乘也就是ATPA=min,其中由于A中存在偏差,则其偏差的协方差因噪声误差的影响而增加。所以,在考虑系数矩阵A中存在偏差时,应考虑采用其他的推广最小二乘配置方法[5]。由于总体最小二乘算法中,解算方法多样,本文采用传统的迭代算法[6]。
4 不同坐标转换求解算法的计算结果及对比分析
4.1应用实例
本文采用某测区11个工程实测重合点的WGS-84和1980西安坐标系,利用MATLAB软件编程,进行计算对比分析,坐标数据见表1,由于测绘数据的保密性,坐标数据的前5位省略。

表1 工程实例数据
4.2不同坐标转换求解算法计算结果对比与分析
在此针对最小二乘算法,坐标重心化算法,最小二乘分解算法,基于尺度因子求解算法,总体最小二乘算法这5种算法进行分析。因测区呈面状,1、2、3、4、5号点为四等点,保存较好,1、2、3号点相对分布均匀,6、7、8、9、10、11号点为一级点,为此设计两种方案:计算方案一,以1、2、3号点作为公共点,4、5号点作为检验比对点;计算方案二,以1、2、3、4、5号点作为公共点,10、11号点作为检验比对点。分别以5种方法计算转换参数并将WGS-84坐标系坐标转换为1980西安坐标系坐标,根据计算结果进行对比分析。结果显示:两种方案计算结果一致,因篇幅限制仅列出方案1的计算成果。
应用MATAB软件编程,得到几种不同转换算法求解的转换参数,见表2。

表2 坐标转换参数
表2(续)

转换参数传统最小二乘算法重心化求解算法最小二乘分解算法尺度因子求解算法总体最小二乘算法ΔZ4.35329687375.45866666674.3532968564.37606401774.3729663268m-0.0000011261-0.0000089755-0.0000011261-0.0000011343-0.0000011341εX0.00000291052-0.00000032390.000002910520.00000291050.0000029010εY-0.00000668760.0000105875-0.000006687639-0.0000066876-0.00000668751εZ0.000017087480.99999571460.00001708750.00001708750.00001708671
求得转换参数后,对4、5号点进行坐标转换,得到的坐标残差及点位偏差,见表3。

表3 坐标点位残差及偏差
通过表2及表3对比发现:坐标重心化算法求解转换参数偏差较大,其余4种算法坐标转换参数结果相当;坐标重心化求解方法得出的4、5号点位偏差分别为215.590 7 mm与389.243 4 mm,而其余4种算法得出的4、5号点位偏差平均值分别为6.550 9 mm与6.321 0 mm。
5 结论
通过前文的分析,笔者得出如下结论:
1)传统最小二乘算法和最小二乘分解算法结果一致,尺度因子求解算法和总体最小二乘算法结果一致,这4种算法求得的坐标转换参数和坐标转换结果相当,能保证精度,具有可靠性;
2)坐标重心化算法实施坐标转换计算误差较大,从理论上分析其根本原因是布尔沙模型旋转参数和平移参数相关性较强[7],坐标重心化算法中因原点重心化改变了平移性质进而影响旋转参数求解精度,导致转换误差较大,实际应用中坐标重心化算法不适宜于布尔沙模型。
[1]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2002.
[2]鲁铁定,宁津生,周世健,等.最小二乘配置的QR分解解法[J].辽宁工程技术大学学报:自然科学版,2009,28(4):550-553.
[3]田红平.一种利用坐标重心求解坐标转换关系式的方法[J].山西建筑,2011,37(15):197-198.
[4]李卓昌.坐标转换求解算法及模型误差分析与研究[D].昆明:昆明理工大学,2015.
[5]陆珏,陈义,郑波.总体最小二乘方法在三维坐标转换中的应用[J].大地测量与地球动力学,2008,28(5):77-81.
[6]孔建,姚宜斌,吴寒.整体最小二乘的迭代解法[J].武汉大学学报:信息科学版,2010(6):711-714.
[7]王解先.七参数转换中参数之间的相关性[J].大地测量与地球动力学,2007,27(2):43-46.
Analysis and Research on Algorithm of Coordinate Transformation
LI Yong1,YANG De-hong2
(1.Dali Institute of Land and Resources Planning and Research,Dali Yunnan 671000,China; 2.College of Land and Resources Engineering,Kunming University of Science and Technology,Kunming Yunnan 650093,China)
In the practice of geodetic surveying and engineering surveying,it is inevitable to solve the problem of establishment of measuring coordinate system and coordinate transformation.This paper analyses and studies 5 kinds of coordinate transformation algorithm based on the Bursa model.The related calculation and comparison analysis are carried out by using engineering instance data and MATLAB software programming.The results indicate that using coordinate centralization algorithm to solve conversion parameters and coordinate appear abnormal.Through the calculation results and theoretical analysis,the coordinate centralization algorithm is not suitable for Bursa model.The coordinate conversion parameters and results obtained by the other 4 algorithms are very close,and can ensure the accuracy.Therefore,the other 4 algorithms are reliable.
Bursa model;coordinate transformation algorithm;comparative analysis
2016-04-01
P 226+.3
B
1007-9394(2016)03-0029-03
李勇(1975~),男,云南大理人,学士,高级工程师,现主要从事工程测量与土地规划设计方面的工作。
