药物作用量-效关系的Thiele型连分式插值法分析

朱　涛，赵前进，李朝品

(1.安徽理工大学　医学院，安徽　淮南　232001;2.安徽理工大学　理学院,安徽　淮南　232001;3.皖南医学院　医学寄生虫学教研室，安徽　芜湖　241002)



·基础医学·

药物作用量-效关系的Thiele型连分式插值法分析

朱涛1，赵前进2，李朝品3

(1.安徽理工大学医学院，安徽淮南232001;2.安徽理工大学理学院,安徽淮南232001;3.皖南医学院医学寄生虫学教研室，安徽芜湖241002)

目的：提出Thiele型连分式插值法，研究并建立新的量-效关系分析方法。方法：以原卟啉钠(NAPP)抑制人肝癌细胞株SMMC-7721细胞增殖的实验数据为例，基于Thiele型连分式插值，求出量-效关系表达式并绘制量-效曲线图；预测最大抑制率，计算半抑制浓度(half inhibitory concentration，IC50)和半效浓度(half effective concentration，EC50)；求导并绘制导数图，研究抑制率随药物浓度变化的快慢程度。结果：通过Thiele型连分式插值法，得出NAPP作用于SMMC-7721细胞24、48、72 h的量-效关系表达式，预测不同时间下最大抑制率分别为43.75%，55.97%，64.93%；EC50分别为1.04 mg/L、0.36 mg/L、0.30 mg/L；作用48 h、72 h后IC50分别为 16.46 mg/L、8.26 mg/L。导数图表明NAPP浓度在10 mg/L内，抑制率随浓度变化速度快，药效不稳定；大于10 mg/L后，变化不明显，药效稳定，出现平台期。结论：Thiele型连分式插值法简单、实用，逼近效果好，可作为研究药物量-效关系的一种新方法。

原卟啉钠；SMM-7721细胞；量-效关系；导数；有理逼近；连分式插值

药物作用量-效关系是评价药物药效的重要参考指标[1]，而这种量-效关系多表现为非线性特征，研究者常用计算软件中的数学模型对实验数据进行非线性曲线拟合，这些模型利用诸如最小二乘法等原理[2]的逼近效果，得到拟合曲线方程，以此帮助研究量-效关系。在实际研究中，有些非线性回归模型过于复杂,利用它求解方程困难，如常用的logistics数学模型等[3]；还有些模型因参数难以估计，不能化为线性回归模型进行简便处理。因此，本研究基于Thiele型连分式插值[4-6]建立简单的有理函数分析方法，提出一种运算便捷、逼近效果[7]好的新方法来研究量-效关系的非线性特征。现将研究结果报道如下。

1　资料与方法

1.1资料依据文献[8]从猪血中提取原卟啉钠(protoporphyrin disodium,NAPP)，采用MTT比色法，依据不同浓度NAPP在24、48、72 h抑制人肝癌细胞株SMMC-7721细胞增殖的实验研究结果[8]，见表1。

表1不同浓度NAPP作用不同时间后对SMMC-7721细胞增殖抑制率的影响

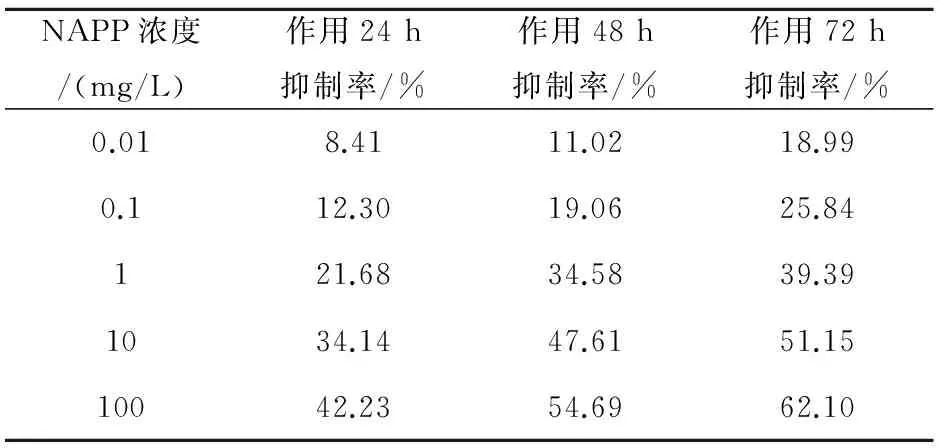
NAPP浓度/(mg/L)作用24h抑制率/%作用48h抑制率/%作用72h抑制率/%0.018.4111.0218.990.112.3019.0625.84121.6834.5839.391034.1447.6151.1510042.2354.6962.10

1.2方法

1.2.1Thiele型连分式插值法设点集X={x0,x1,……,xn}⊂[a,b]，函数f(x) 在[a,b]上有定义。X上的Thiele型连分式插值为：

φ[xp]=f(xp),p=0,1,……n,

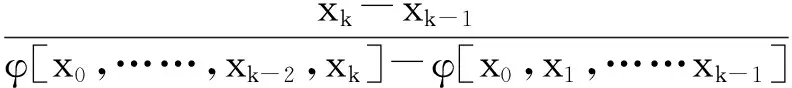
设定x轴为药物浓度，y轴为抑制率，利用Thiele型连分式插值，求得有理插值函数作为量-效关系表达式。当n变大时，会导致函数Rn(x)振荡加剧，同时使舍入误差的扩散加剧[9-10]。另外，当n选择为奇数时，有理插值函数的分子分母多项式次数相同，才可能有水平渐近线，符合药物作用量-效关系曲线应有的特征。因此，本研究中选择n=5。

1.2.2其他数据处理方法运用Maple17.0，运行Thiele型连分式插值命令语句，求量-效关系有理函数表达式；依据量-效关系有理函数表达式，运用Matlab8.0绘制量-效关系曲线图、导数图；使用Maple17.0计算表达式，求解量-效关系相关参数，如最大极限值、半抑制浓度(IC50)和半效浓度(EC50)。

2　结果

2.1NAPP抑制SMMC-7721细胞增殖的量-效关系表达式①作用24h后，依据不同的药物浓度及对应的抑制率，得到五个插值点，分别为(0.01，8.41%)、(0.1，12.30%)、(1，21.68%)、(10，34.14%)、(100，42.23%)，得到量-效关系表达式：

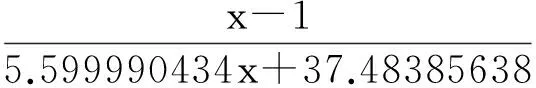
②作用48 h后，同法得到五个插值点，分别为(0.01，11.02%)、(0.1，19.06%)、(1，34.58%)、(10，47.61%)、(100，54.69%)，得到量-效关系表达式：

③作用72h后，同法得到五个插值点，分别为(0.01，18.99%)、(0.1，25.84%)、(1，39.39%)、(10，51.15%)、(100，62.10%)，得到量-效关系表达式：

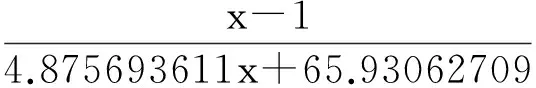
2.2量-效关系曲线图根据24、48、72h量-效关系表达式，绘制NAPP抑制SMMC-7721细胞增殖的量-效曲线，如图1所示。

图1不同时间NAPP抑制SMMC-7721细胞增殖量-效曲线

2.3相关参数计算①最大抑制率(ECmax):令x→+∞,对上述2.1中的各表达式取极限，计算出NAPP作用SMMC-7721细胞24、48、72h后，ECmax分别为43.75%，55.97%，64.93%，图1中可见。②IC50与EC50：令抑制率y=50%，计算NAPP作用SMMC-7721细胞48、72h后的表达式，得出IC50分别为16.46mg/L、8.26mg/L。分别与SPSS、曲线回归法的计算结果比较，见表2。令抑制率y=50%×ECmax，计算NAPP作用SMMC-7721细胞各时段的表达式，得出EC50分别为1.04mg/L、0.36mg/L、0.30mg/L。

表2三种方法对半数抑制浓度计算的结果

mg/L

2.5导数图根据各量-效关系表达式，求导得出SMMC-7721细胞增殖抑制率对NAPP浓度的导数，即变化率，绘制二者之间的导数图，如图2所示。

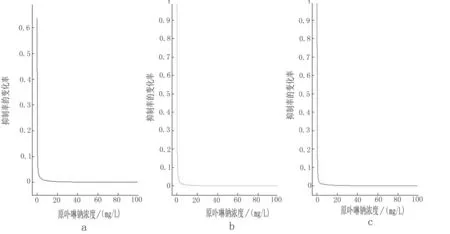
a.Effect of 24 h;b.Effect of 48 h;c.Effect of 72 h

图2NAPP浓度-抑制率变化率的导数图

3　讨论

3.1量-效曲线表达式简单，逼近程度高，预测结果可信度高本研究采用的Thiele型连分式插值法是一种简单的有理函数方法，利用其分析药物作用量-效关系为非线性关系，可进行理论分析和预测分析，如在对比研究IC50结果时，发现NAPP作用SMMC-7721细胞24 h后，预测抑制率最大值仅43.75%，未能达到IC50，与许金鹏等研究结果不同，见表2。而基于统计学方法的常用分析法在进行Probit分析时，使用概率或Logit数学模型，不能准确分析出各时段的最大效应值，使得在该模型分析下，最大效应都是100%，此时IC50、EC50结果相等，可见其分析偏差大。另外，Probit分析的结果是估计值，逼近效果一般。所以，在预测各时段NAPP最大抑制率的前提下，本方法可准确分析量-效关系，逼近实验结果程度高，计算IC50、EC50结果更真实。

3.2量-效关系曲线图与导数图从图1中的量-效曲线图可见，不同浓度NAPP作用不同时间，其抑制率与浓度呈正比关系，量-效曲线呈先陡后平形态，在顶部均呈水平状态，此时浓度增加，但抑制效果不再有显著变化，符合量-效曲线特征[11]。另外，图1中的量-效曲线准确通过各实验数据点，保证了实验数据的原始特征，如实反映每个点上的曲线特征，它模拟了药物浓度与抑制率量-效关系变化的全过程，反映NAPP抑制肝癌细胞增殖的量-效关系。

导数图可直观的反映药物浓度与抑制率之间的变化率，导数曲线越接近零，表示药物浓度与抑制率量-效关系变化越稳定。由图2可见，作用不同时间后，NAPP浓度在10 mg/L内，抑制率变化幅度大，药效变化显著，不稳定。10 mg/L之后，变化率趋近于0，几乎与横坐标重叠，表明药效稳定，药物浓度增加，抑制效果变化不显著。因此，导数图为药物浓度的选择量提供可靠的参考依据。

3.3存在的问题在使用连分式插值法作逼近时，可能会出现Rn(x)在插值区间内有极点[12]的情况，此时预测结果可能会出现较大误差，这种情况下本方法将不再适用。因此，极点问题的处理也是今后本研究需要继续深入讨论的问题。

4　结论

在药物研究领域中，目前常用概率单位法[13]、线性回归法[14]、曲线拟合等方法来研究非线性量-效关系，但这些方法使用较为复杂，且条件限制较多，实验数据在线性与非线性的转换过程中，不能保存原始数据的变化特征，丢失各数据点的曲线特征，同时，使用统计学方法处理数据量较少的实验数据，会导致估算误差较大。因此，采用Thiele型连分式插值法分析药物作用量-效关系，不仅逼近程度高，而且更是一种运算简单、效果显著且易于掌握的新方法。

[1]吕圭源,药理学[M].北京:中国中医药出版社,2009:7.

[2]肖爱玲,非线性最小二乘法的算法[J].数学理论与应用，2004,24(2):86-90.

[3]顾兵,张政,李玉萍,等.半数致死剂量及其计算方法概述[J].中国职业医学，2009，36(6):506-511.

[4]檀结庆.连分式理论及其应用[M].北京:科学出版社，2007:30-120.

[5]LU DAWEI,SONG ZEXI.Some new continued fraction estimates of the Somos′ quadratic recurrence constant[J].Journal of Number Theory,2015,155(10):36-45.

[6]LISA LORENTZEN.A convergence theorem for random continued fractions[J].Journal of Approximation Theory,2015,197(9):1-8.

[7]朱功勤,顾传青,檀结庆.多元有理逼近方法[M].北京:中国科学出版社,2007:10-91.

[8]许金鹏,张慧慧,李朝品,等.原卟啉钠体外对人肝癌细胞株SMMC-7721细胞的抑制作用[J].中国实验方剂学杂志,2011,17(18):173-178.

[9]李庆扬,王能超,易大义.数学分析[M].5版.北京:清华大学出版社,2008:79-81.

[10] 周志丹.回归函数的有理逼近模型分析与研究[J].数学的实践与认识,2004,34(7):113-117.

[11] 杨宝峰.药理学[M].8版.北京:人民卫生出版社,2013:22-24.

[12] 项赟飚.构造矩阵有理插值函数降阶的方法[J].合肥工业大学学报(自然科学版),2010,33(8):1277-1280.

[13] 赵劲松,于书霞.利用概率单位法估算EC50的研究[J].生态毒理学报,2010,5(3):421-425.

[14] 李翠萍,吴民耀,王宏元.3种半数致死浓度计算方法之比较[J].动物医学进展,2012,33 (9):89-92.

Estimation of the drug dose-effect relationship by thiele-type continued fraction interpolation

ZHU Tao,ZHAO Qianjin,LI Chaopin

School of Medicine,Anhui University of Science and Technology,Huainan 232001,China

Objective：To design a thiele-type continued fraction interpolation for estimation of the dose-effect relationship of drugs.Methods:The experimental data on the inhibitive effect of protoporphyrin disodium(NAPP) on human hepatoma carcinoma strain of SMM-7721 cells in vitro were collected and thiele-type continued fraction interpolation was used to prepare the equation of dose-effect and plot the curves,and to estimate the maximum value of inhibition rate.Half inhibitory concentration(IC50)and half effective concentration(EC50) were computed,and the derivative was driven and the derivative graph was developed for examining changes of inhibition rate with the level of NAPP.Results:Thiele-type continued-fraction interpolation obtained the equation of dose-effect relationship pertaining to the inhibitive effect of NAPP on SMM-7721 cells at 24,48 and 72 h,and prediction of the maximum value of inhibition rate at the corresponding time point by 43.75%,55.97% and 64.93%,respectively.The EC50was 1.04 mg/L,0.36 mg/L and 0.30 mg/L;and IC50at 24-hour and 48-hour,16.46 mg/L and 8.26 mg/L.The derivative graph indicated that the inhibition rate changed with NAPP concentration at 10 mg/mL,yet the drug effect appeared unstable.The variation was not significant,and the drug effect remained stable and in plateau derivative as the NAPP concentration excelling 10 mg/L.Conclusion： Thiele-type continued-fraction interpolation is simple,practical and effective,with a good approximation effect in comparison with other algorithms,and can be used as a new method for the study of dose-effect relationship of drugs.

protoporphyrin disodium;SMM-7721 cell;dose-effect relationship;derivative;rational approximation;continued fraction interpolation

1002-0217(2016)05-0414-04

国家自然科学基金项目(60973050);安徽省高校省级自然科学研究基金项目(KJ2008A099)

2016-05-04

朱涛(1979-)，男，讲师，硕士，(电话)13956455583，(电子信箱)kwk@aust.edu.cn；

【文献标识码】A

10.3969/j.issn.1002-0217.2016.05.002

李朝品，男，教授，(电子信箱)cpli001@126.com，通信作者.