不确定高阶MIMO系统的指对数型终端滑模控制
2016-10-27傅佳烨牛玉刚华东理工大学化工过程先进控制和优化技术教育部重点实验室上海200237
傅佳烨, 牛玉刚(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)
不确定高阶MIMO系统的指对数型终端滑模控制
傅佳烨, 牛玉刚
(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)
针对一类不确定高阶MIMO线性系统,提出了一种新型指对数型终端滑模控制方法。所设计的非线性指对数型终端滑模面,不仅能保证滑模动态的有限时间稳定,而且具有更快的收敛速度。同时,滑模控制器能够保证滑模面的有限时间可达性。最后,通过数值仿真验证了本文方法的有效性。
终端滑模控制;MIMO系统;指对数型
在实际工业生产过程中,控制系统常常受到各种不确定性的影响,包括系统参数摄动以及外界干扰等,这些不确定性不仅会影响系统性能,严重时甚至会导致系统失稳,因而对于不确定系统的研究一直都是控制领域的研究热点。滑模变结构控制由于其对系统参数摄动以及外界干扰具有良好的鲁棒性[1],成为处理不确定系统控制问题的一种有效的鲁棒控制方法。
传统的线性滑模面虽然能保证系统状态沿滑模面渐近稳定(即当时间趋于无穷大时,状态渐近收敛于状态原点),却不能实现有限时间收敛。然而在许多实际应用中(例如刚性机器人的控制、航天航空中的飞行器控制等),常常要求系统状态能够在有限时间内收敛到平衡点。终端滑模控制(Terminal Sliding Mode Control,TSMC)方法正是针对这个问题提出的[2-3],其主要思想是采用非线性滑模面,使得系统状态到达滑模面后能够在有限时间内收敛到平衡点。针对二阶系统,文献[4-7]分别提出了快速、指数型、对数型、指对数型等终端滑模面,提高了系统状态在滑模面上的收敛速度。文献[8-9]提出非奇异终端滑模面,解决了终端滑模控制的奇异性问题。文献[10]提出了非奇异快速终端滑模面。然而,针对高阶MIMO线性系统,终端滑模控制的研究成果相对比较少[11-14],主要是因为终端滑模最初是针对二阶系统提出的,不像传统的线性滑模控制方法,很难直接推广到高阶多输入系统。这也是目前终端滑模控制在高阶多输入系统研究中的一个难点。
本文针对一类不确定高阶MIMO线性系统,提出了一种新型指对数型终端滑模面,同时设计相应的滑模控制器,使得系统状态能够在有限时间内收敛到平衡点,且收敛速度快于已有的高阶终端滑模控制。
1 系统描述
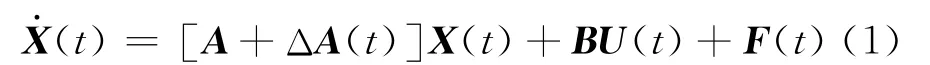
其中:X(t)∈Rn为系统状态变量;U(t)∈Rm为系统控制输入;A∈Rn×n和B∈Rm×n是已知的系统参数矩阵;ΔA(t)和F(t)分别代表未知的系统参数摄动矩阵和外界干扰。假定系统满足以下假设:
(1)标称系统(A,B)可控,且B列满秩;(2)ΔA(t)、F(t)满足以下匹配条件:

不同于文献[11],本文考虑的系统模型满足式(2)~式(3)所示的匹配条件,是为了在后面的设计过程中使得系统状态在有限时间内收敛到平衡点,而不是平衡点附加的一个邻域内。
考虑如下不确定高阶MIMO线性系统
2 指对数型终端滑模面的设计
2.1系统模型转换
由B列满秩可知,存在可逆矩阵T使得TB= [0 B2]T成立,其中B2∈Rm×m是满秩矩阵,且有
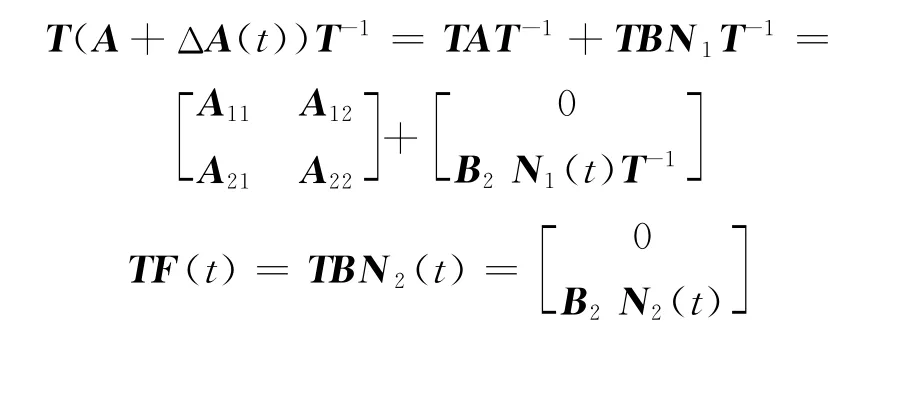

由于Z(t)与X(t)呈线性关系,当Z(t)→0时,X(t)→0。这样所研究的问题等价于对系统(4)进行终端滑模设计,使系统状态在有限时间内收敛到零。
2.2指对数型终端滑模面设计及稳定性分析
文献[7]提出了如下的指对数型终端滑模面:
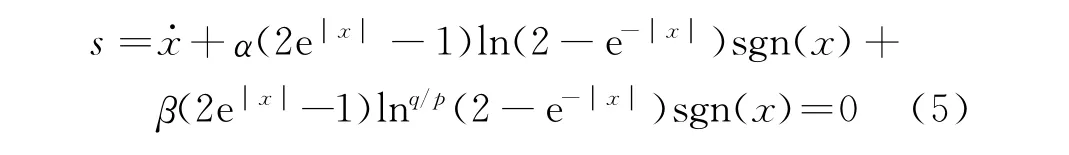
式中:x∈R;a>0;β>0;p,q满足q<p<2q且为正奇数。从式(5)可以看出,一般指对数型终端滑模面适用于SISO系统,而不能直接应用到MIMO系统。
本文将式(5)所示的指对数型终端滑模面拓展到式(4)所示的MIMO系统中,设计指对数型终端滑模面为
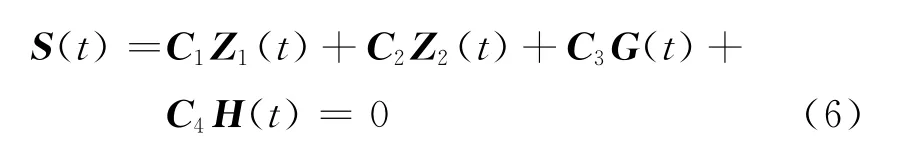
式中,G(t)和H(t)分别定义如下:
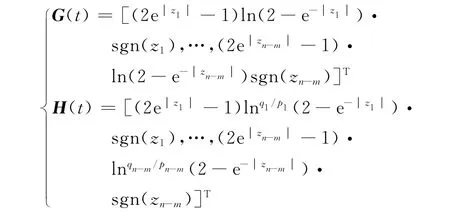
其中:pi,qi满足qi<pi<2qi,(i=1,…,n-m)且为正奇数。
另外,式(6)中C1∈Rm×(n-m),C2∈Rm×m,C3∈Rm×(n-m),C4∈Rm×(n-m)为终端滑模面的参数矩阵,其中C2是一个满秩矩阵,即rank(C2)=m。设计C1、C2、C3、C4满足以下条件:
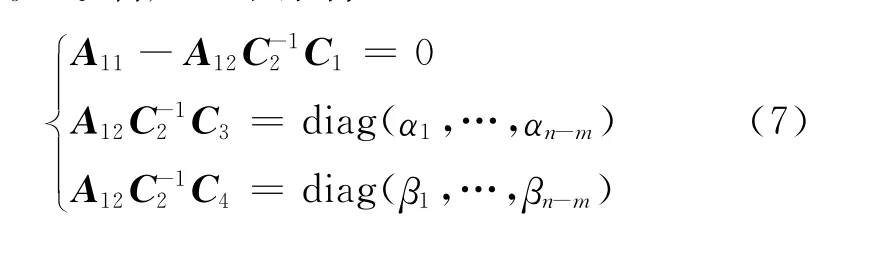
其中,ai>0,βi>0,(i=1,…,n-m)。
按照滑模控制理论,当系统(4)沿指对数型终端滑模面式(5)运动时,系统的状态方程降为n-m阶。由式(5)可以得到
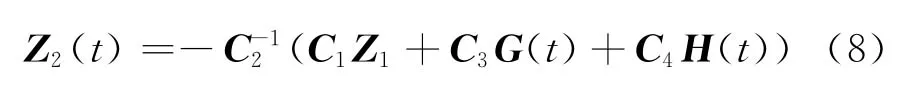
将式(8)代入式(4),可以得到n-m阶滑模动态方程为
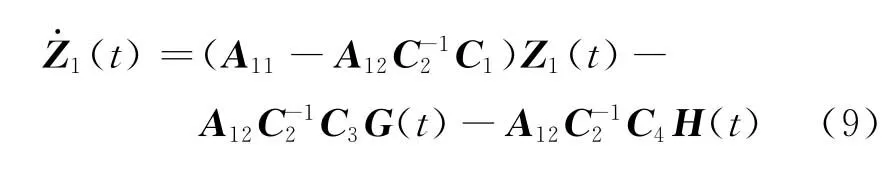
下面分析不确定高阶MIMO系统沿指对数型终端滑模面(式(6))运动时,系统动态在有限时间内收敛到平衡点,同时系统(8)也在有限时间内收敛到平衡点。
定理1 对于不确定高阶MIMO线性系统(4),设计指对数型终端滑模面(式(6)),且滑模面参数矩阵满足条件式(7),则系统状态Z1(t)在到达滑模面后将在有限时间内收敛到平衡点,同时Z2(t)也将在有限时间内收敛到平衡点。
证明
(1)稳定性。当系统状态变量进入滑模面后,可以得到式(9)所示的滑动模态方程,将滑模面参数矩阵条件式(7)代入式(9),有
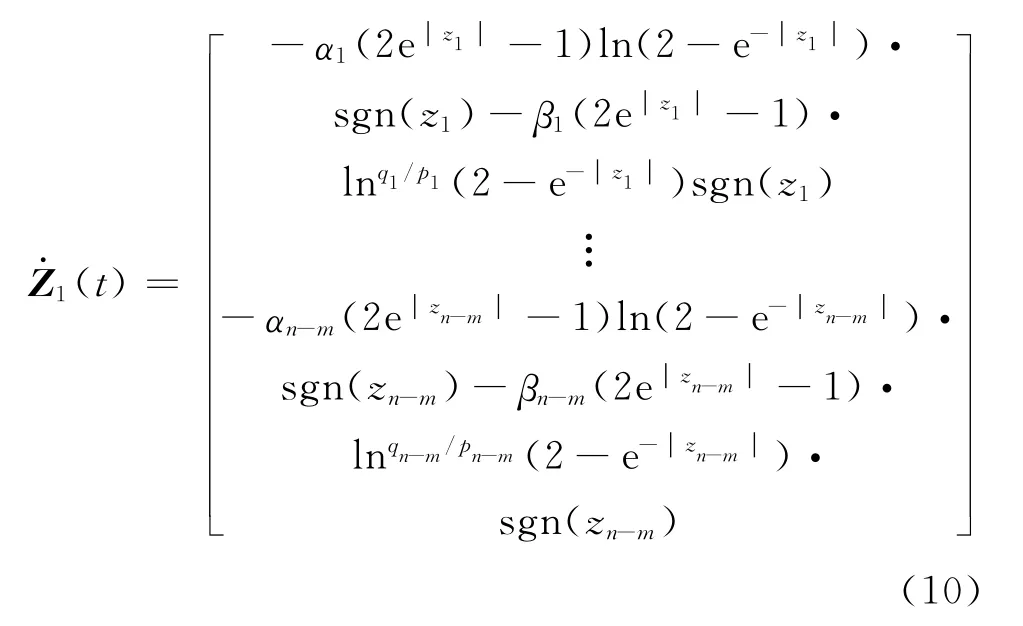
即Z1(t)每个标量zi均满足:
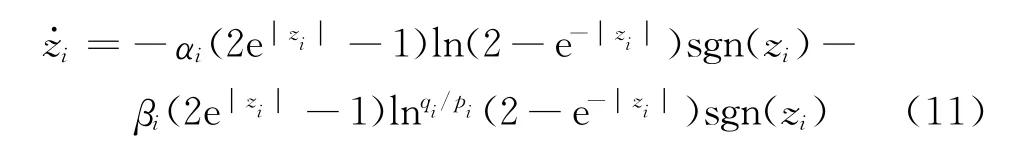
由式(11)可知,zi满足一般指对数型终端滑模面的形式。
选取Lyapunov函数V1:
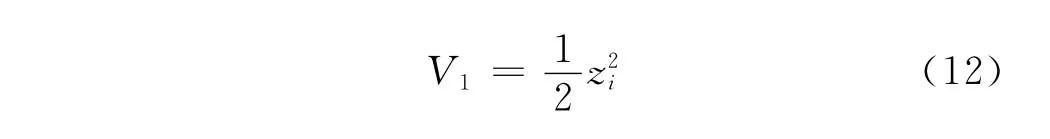
对式(12)求导,可得
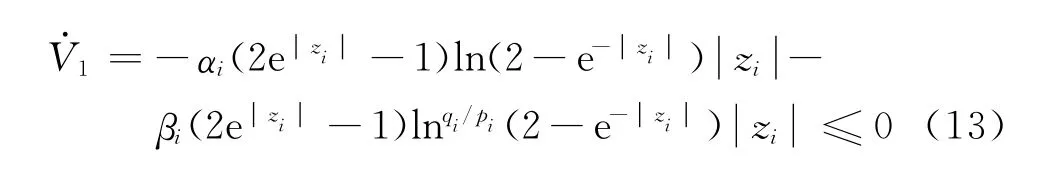
由Lyapunov稳定性定理可知,系统是稳定的。
(2)有限时间可达。当系统状态到达滑模面时,由以上分析过程可知,式(11)可以表示为
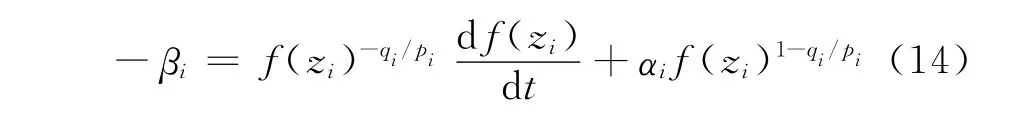

由式(14)、式(15)可得
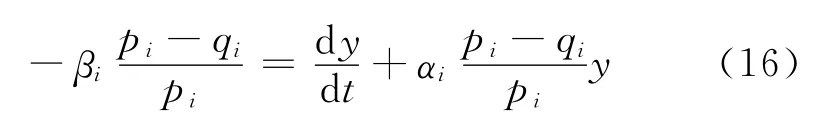
由一阶线性微分方程通解求解理论,式(16)的解为
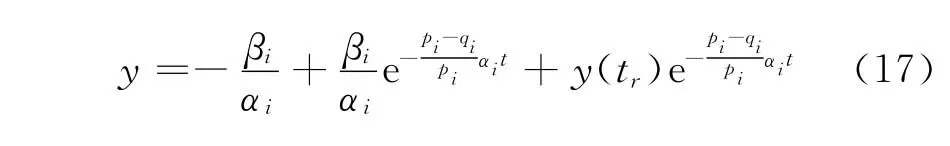
其中,tr为系统从任意初始状态到达滑模面的时刻。
我们知道,当系统状态到达平衡点时f(zi,tsi)= 0,即y(tsi)=0。根据式(17),可求得zi将在有限时间tsi内沿滑模面到达平衡点:
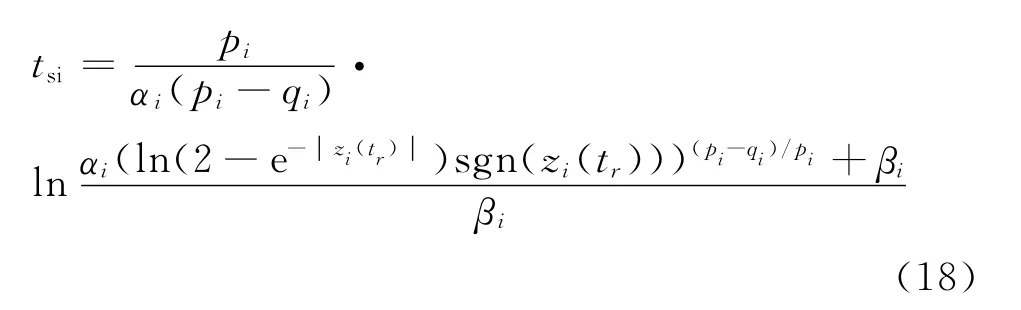
由此证明Z1(t)是有限时间稳定的,并且根据式(8)可知Z2(t)也是有限时间稳定的,即系统状态在到达滑模面后将在有限时间内收敛到平衡点,且有限时间满足证毕。
3 终端滑模控制器的设计
对式(19)求导,可得
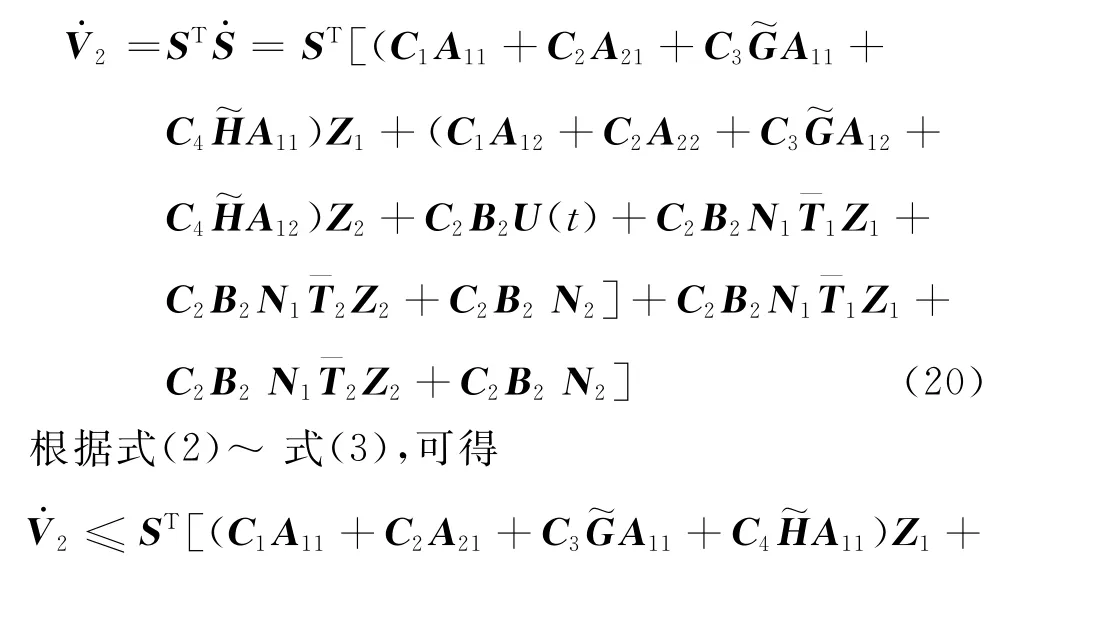
定理1给出了系统状态沿终端滑模面有限时间稳定的充分条件。进一步设计终端滑模控制器保证系统状态轨迹能在有限时间内到达滑模面S(t)=0。
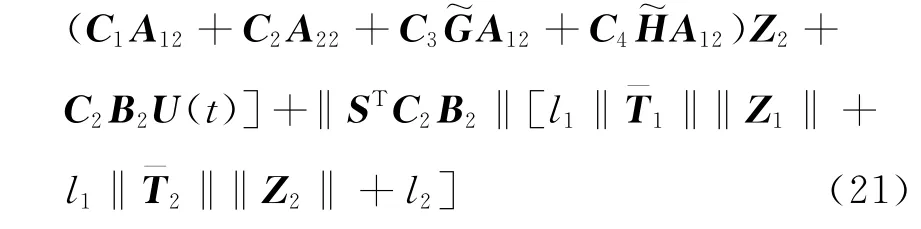
为使滑动模态的可达性条件成立,设计终端滑模控制器如下:
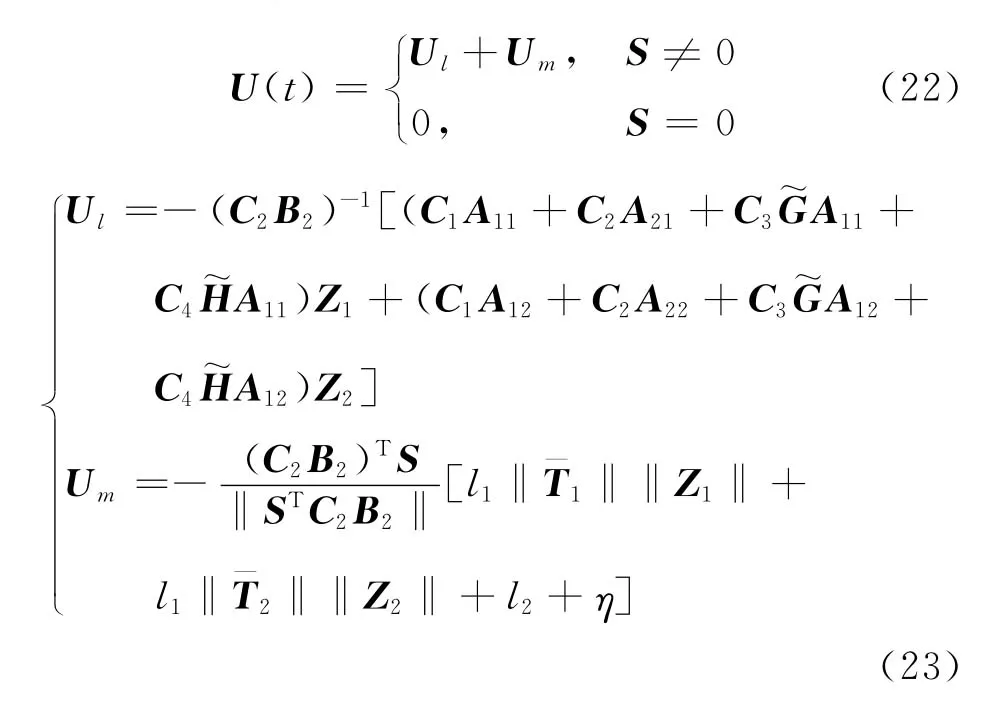
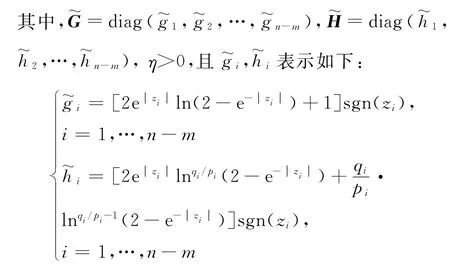
将所设计的终端滑模控制器式(22)、式(23)代入式(21),可以得到
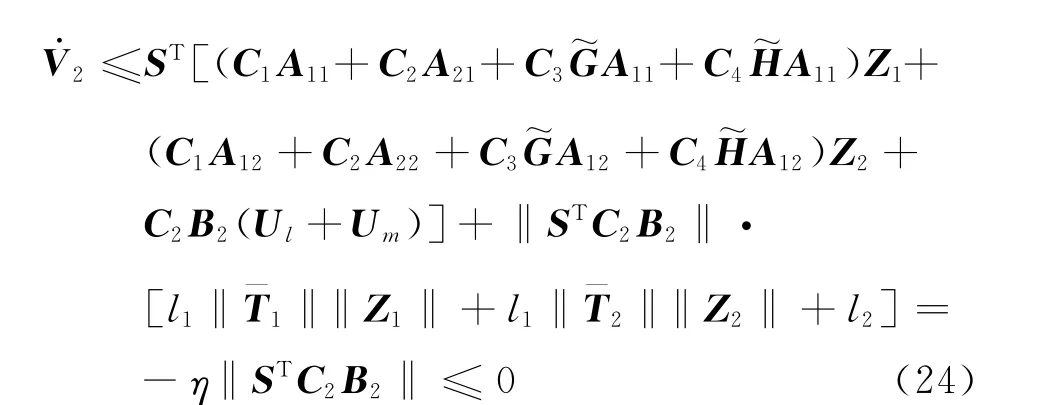
由Lyapunov稳定性定理可知,系统(4)在有限时间内到达滑模面,收剑时间满足
由以上分析过程可以得到定理2。
定理2 对于不确定高阶MIMO系统(4)和指对数型终端滑模面(式(5)~式(7)),终端滑模控制器为式(22)、式(23)可以保证系统(4)在有限时间内到达滑模面S=0。
由定理1和定理2可知,对于任意初始状态,系统状态Z(t)将在有限时间t=ts+tr内到达平衡点,因此,系统状态X(t)将在有限时间内到达平衡点。
4 仿真研究
考虑不确定高阶MIMO系统(1),其参数分别为
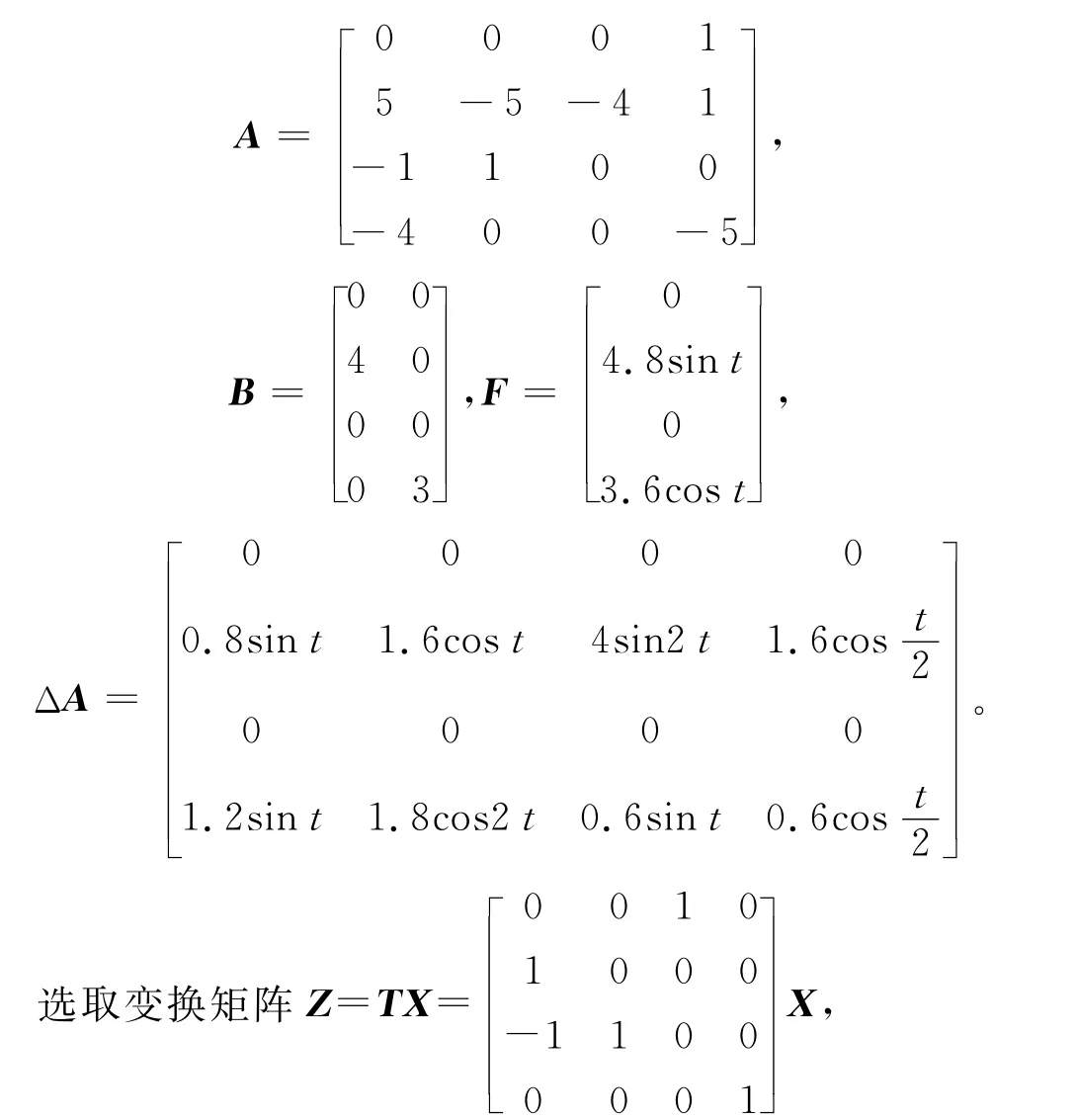
则变换后系统(4)的参数分别为
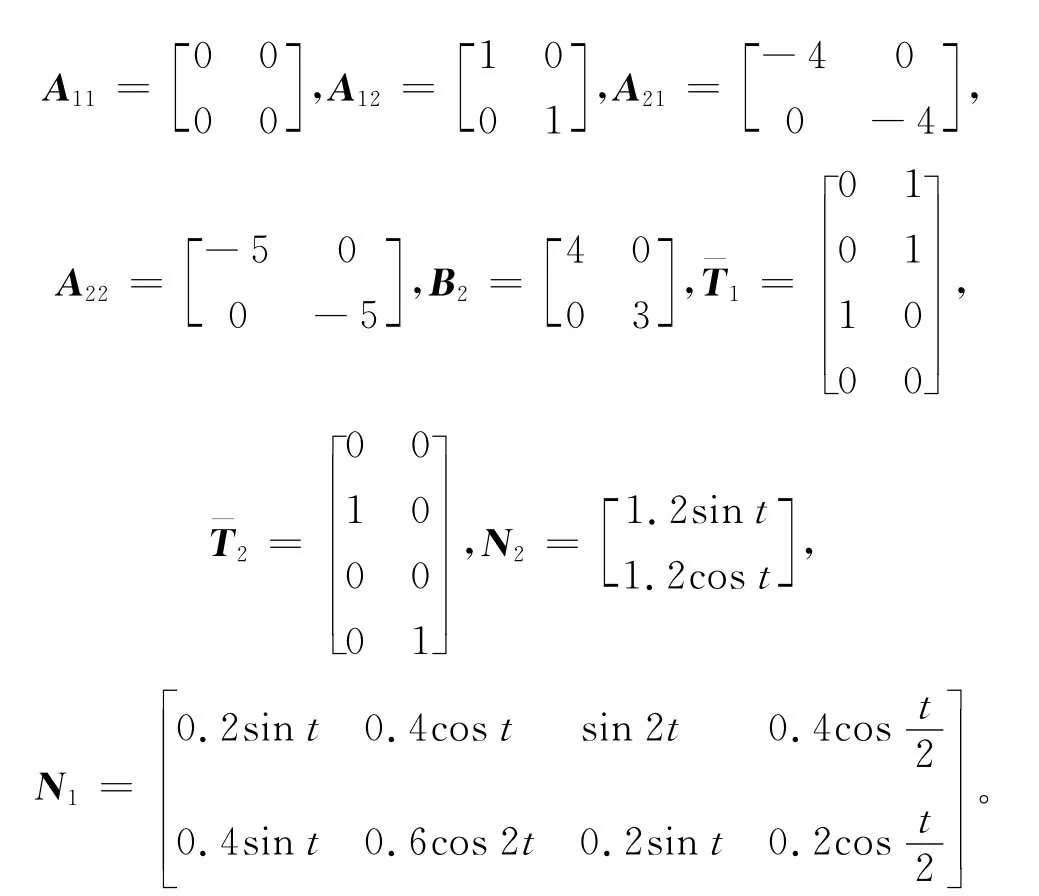
根据滑模面参数矩阵满足条件式(7),选取指对数型终端滑模面各参数如下:
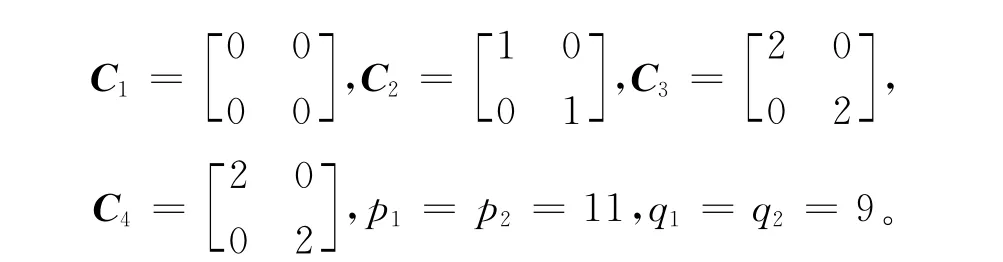
按照所设计的滑模控制器(式(19)~式(20)),选取控制器各参数:
为验证本文设计的指对数型终端滑模控制(ELTSMC)的有效性,分别与已有的快速终端滑模控制(FTSMC)和指数型终端滑模控制(ETSMC)进行仿真比较。其中,快速终端滑模控制为
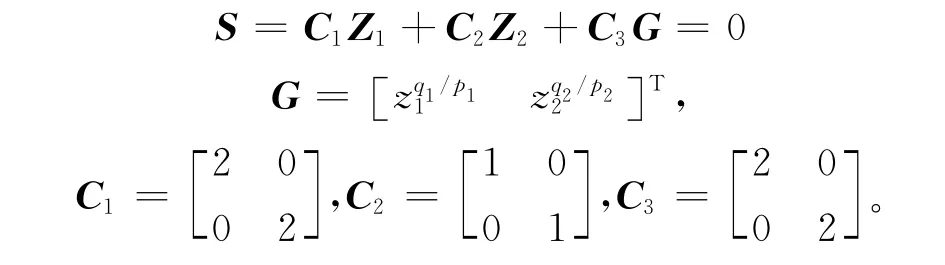
指数型终端滑模控制为
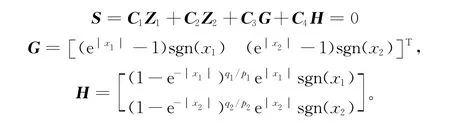
其余参数相同,仿真步长设为0.1 s,系统初始状态X(0)=[-0.4-0.6 0.5 0.1]T。
图1~图3和图4~图6分别示出了系统状态变量和滑模变量在3种控制方法下的响应曲线。在快速终端滑模控制方法下,系统状态经过大约1.7 s到达滑模面;在指数型终端滑模控制方法下,系统状态1.4 s左右后到达滑模面;而本文提出的指对数型终端滑模控制方法可以保证状态到达滑模面所需的时间最短,大约为1.2 s。由仿真结果可知,指对数型终端滑模控制的收敛速度快于快速终端滑模控制和指数型终端滑模控制。
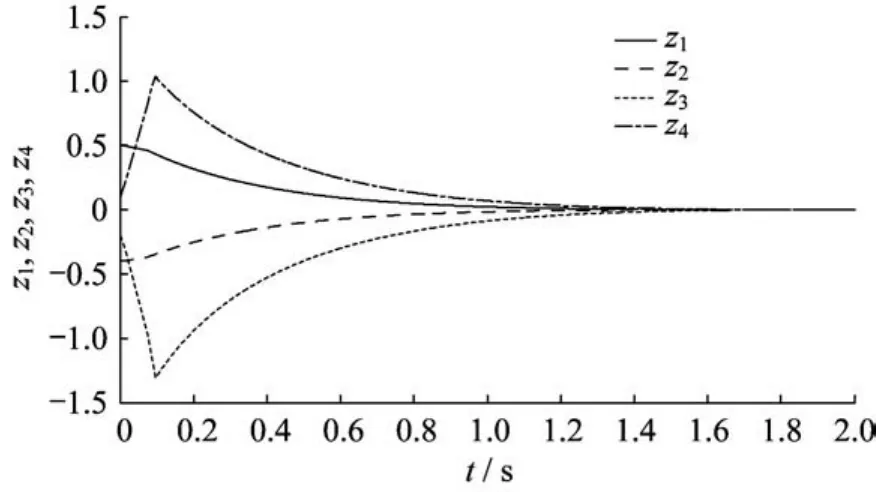
图1 快速终端滑模状态响应曲线Fig.1 System state trajectories of FTSMC
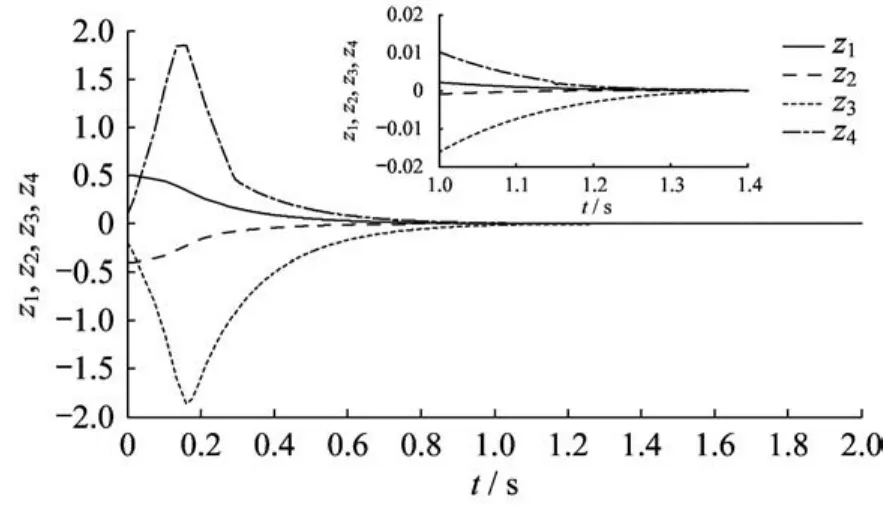
图2 指数型终端滑模状态响应曲线Fig.2 System state trajectories of ETSMC
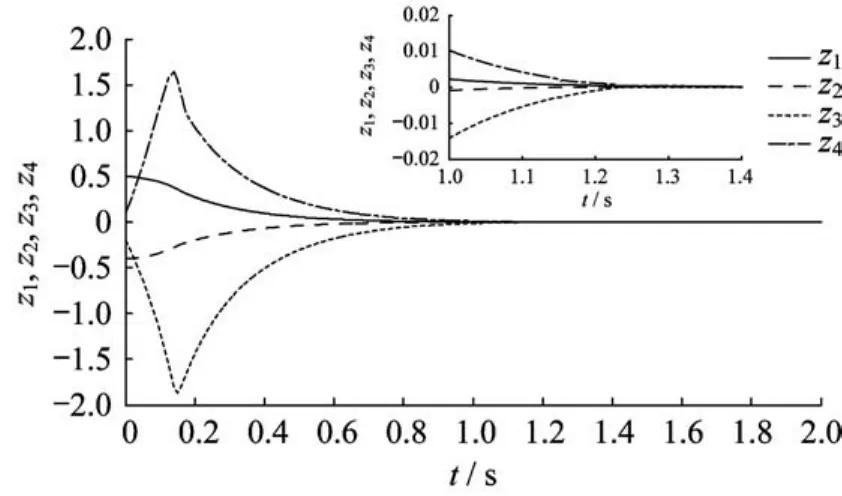
图3 指对数型终端滑模状态响应曲线Fig.3 System state trajectories of ELTSMC
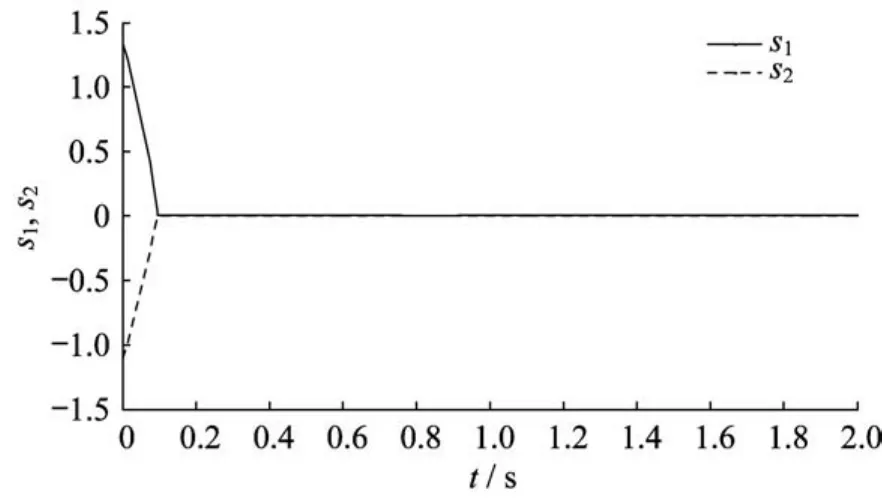
图4 快速终端滑模滑模面曲线Fig.4 Sliding variables trajectories of FTSMC
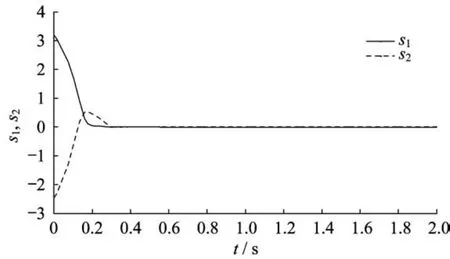
图5 指数型终端滑模滑模面曲线Fig.5 Sliding variables trajectories of ETSMC
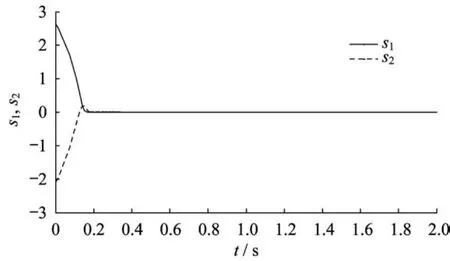
图6 指对数型终端滑模滑模面曲线Fig.6 Sliding variables trajectories of ELTSMC
图7~图9示出了3种控制方法下的控制信号。可以看出,指对数型终端滑模控制方法与快速终端滑模控制方法相比,它的控制输入曲线波动要更大一点;但是与指数型终端滑模控制方法相比,两者的输入曲线波动就相差不大了。
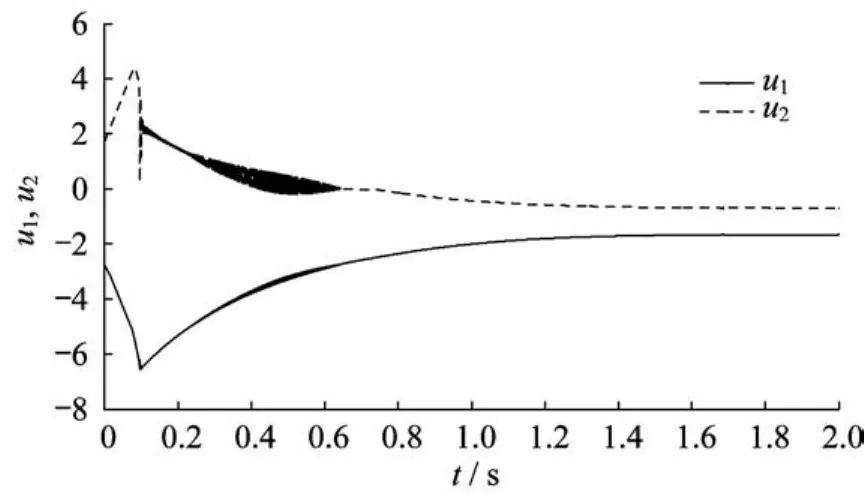
图7 快速终端滑模控制输入曲线Fig.7 Control inputs trajectories of FTSMC
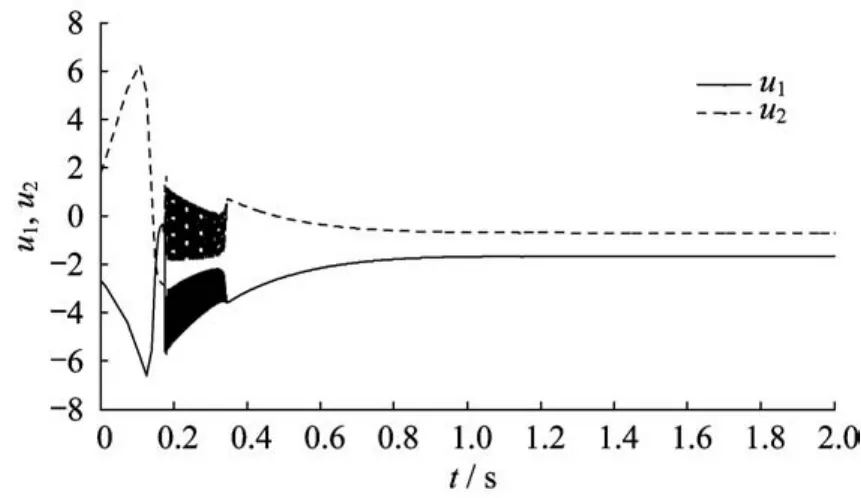
图8 指数型终端滑模控制输入曲线Fig.8 Control inputs trajectories of ETSMC
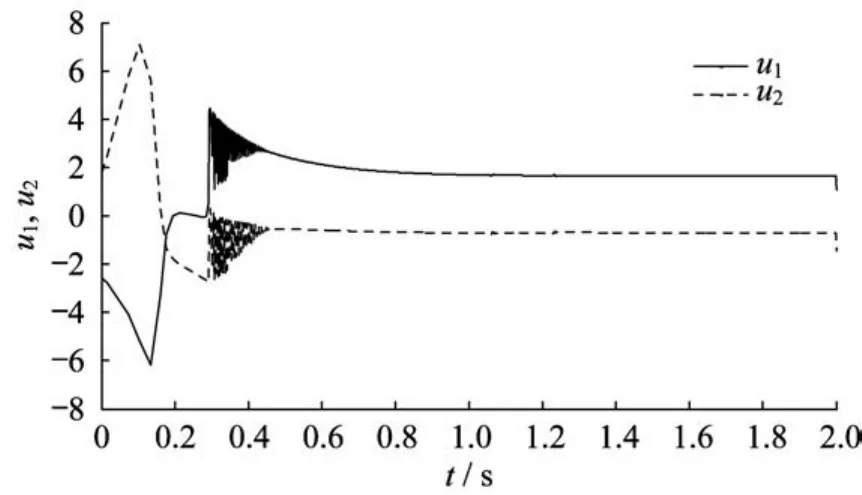
图9 指对数型终端滑模控制输入曲线Fig.9 Control inputs trajectories of ELTSMC
5 结 论
本文研究了不确定MIMO线性系统的终端滑模控制问题,提出了新型指对数型终端滑模控制方法。能够保证不确定MIMO线性系统的全局稳定性,并使系统状态在有限时间内以较快的速度收敛到平衡点,收敛速度快于快速终端滑模控制和对数型终端滑模控制方法,同时对系统的时变不确定部分也有较强的鲁棒性。但是,相较于快速终端滑模控制方法,指对数型终端滑模控制方法的快速收敛性是以控制信号的增大为代价的。因此,如何将控制信号输入波动限定在系统可承受的范围内是下一步工作的重点。
[1] 张晓字,苏宏业.滑模变结构控制理论进展综述[J].化工自动化及仪表,2006,33(2):1-8.
[2] YU Shuanghe,YU Xinghuo,MAN Zhihong.Robust global terminal sliding mode control of SISO nonlinear uncertain systems[C]//Conference on Decision and Control.Sydney,Australia:IEEE,2000:2198-2203.
[3] YU Xinghuo,MAN Zhihong.On finite time mechanism:terminal sliding modes[J].IEEE Workshop on Variable Structure Systems,1996,39(6):164-167.
[4] YU Xinghuo,MAN Zhihong.Fast terminal sliding-mode control design for nonlinear dynamical systems[J].IEEE Transactions on Circuits and Systems,2002,49(2):261-264.
[5] 刘云峰,陈斌文,缪栋.具有强鲁棒性的滑模变结构控制[J].信息与控制,2008,37(2):140-145.
[6] 张秀华,徐炳林,赵宇.有限时间收敛的Terminal滑模控制设计[J].控制工程,2008,15(6):637-639.
[7] 胡志坤,姜斌,陈沅,等.一种指对数型终端滑模控制方法[EB/OL].[2014-03-10].http://jour.blyun.com/views/ specific/3004/CP Detail.jsp?dx Number=330105536887& d=5E8CB01253E72AC13965ABC4EE115C.
[8] CHEN Syuan-Yi,FAA-Jeng.Robust nonsingular terminal sliding-mode control for nonlinear magnetic bearing system [J].IEEE Transactions on Control Systems Technology,2011,19(3):636-643.
[9] DAI Weili,DING Jun,TIAN Hao.Nonsingular terminal sliding mode control for voltage regulation system of doubly salient electro-magnetic generator[C]//SICE Annual Conference.Sapporo:IEEE,2014:715-720.
[10] 李升波,李克强,王建强,等.非奇异快速的终端滑模控制方法[J].信息与控制,2009,38(1):18-21.
[11] 鲍晟,冯勇,郑雪梅.非匹配不确定MIMO线性系统的终端滑模控制[J].控制与决策,2003,18(5):531-539.
[12] 徐世许,马建敏.不确定多变量线性系统的快速收敛滑模控制[J].系统工程与电子技术,2011,33(7):1585-1672.
[13] ZHOU Minghao,FENG Yong,CHEN Bin.High-order terminal sliding-mode control of uncertain systems with mismatched disturbance[C]//Proceedings of the 32nd Chinese Control Conference.Xi’an,China:2013:3190-3193.
[14] 刘根旺,李志强.非匹配时变不确定性时滞系统的Terminal滑模控制[J].系统工程与电子技术,2009,31(5):1180-1183.
An Exponent-Logarithmic Terminal Sliding Mode Control for Uncertain High-Order MIMO Systems
FU Jia-ye, NIU Yu-gang
(Key Laboratory of Advanced Control and Optimization for Chemical Process,Ministry of Education,East China University of Science and Technology,Shanghai 200237,China)
In this paper,an exponent-logarithmic terminal sliding mode control scheme is presented for a class of uncertain high-order MIMO systems.An exponent-logarithmic nonlinear sliding surface is proposed such that the states along the specified sliding surface attain the equilibrium point in finite time with a faster convergence rate.Moreover,a sliding mode controller is designed to guarantee the finite-time reachability of the specified sliding surface.Finally,the simulation results illustrate the effectiveness of the proposed exponent-logarithmic terminal sliding mode control strategy.
terminal sliding mode control;MIMO systems;exponent-logarithmic
TP273
A
1006-3080(2016)01-0085-06 DOI:10.14135/j.cnki.1006-3080.2016.01.014
2015-04-21
国家自然科学基金(61273073,61374107);上海市优秀科技带头人(14XD1420900)
傅佳烨(1990-),女,浙江宁波人,硕士生,研究方向为终端滑模控制。E-mail:940324037@qq.com
牛玉刚,E-mail:acniuyg@ecust.edu.cn
