大连地震台面波震级偏差分析与校正

李慧卿，王九洋，张新杭，原 超，成少云

（大连地震台，辽宁 大连 116012）

大连地震台面波震级偏差分析与校正

李慧卿，王九洋，张新杭，原 超，成少云

（大连地震台，辽宁 大连 116012）

中国地震台网中心提供了一个试算的大连地震台面波震级台基校正模型。基于该模型，我们对1985年至2003年大连地震台记录的共计1357次地震进行了面波震级台基校正试算，按照不同震中距、不同震级、不同方位角分别进行了讨论，得到大多数情况下大连地震台单台实测面波震级小于国家台网面波震级的结论。

震级偏差；面波震级；震中距；反方位角；校正模型

0 引言

在实测中，大连地震台单台面波震级与中国地震台网统一发布的面波震级有一定偏差。这与台站所处地理位置、震源机制、传播路径、甚至瑞利波与勒夫面波的差异等因素都有关［1］：台站所处的地理位置可能对面波的吸收、衰减情况不同［2］；震源机制中，断层错动方向与台站之间的相互位置，直接影响着台站实测最大面波的振幅大小；由于面波是在地球表面传播的，而地球表面传播路径可能存在很大的差异，诸如大陆地壳与海洋地壳这两种传播路径上，面波显示的形态就存在明显差异，而这也必然将影响到面波震级的测定［3］；瑞利面波与勒夫面波本质上是两种性质不同的面波，而实测中是将哪种面波作为最大面波测量，也直接影响着最终的结果。

模拟时期傅盛国（1991）［4］曾测算出大连地震台台基校正值，本文将依据中国地震台网中心提供的一个试算的大连地震台的面波震级台基校正模型详细讨论。

1 面波震级台基校正思路概述

实测中，大连地震台面波震级测定偏差主要表现为：近距离小地震面波震级偏小；不同震中距、不同方位角地震实测面波震级与中国地震台网中心发布的面波震级存在偏差；特定地区的地震面波形态存在明显差异；极远震理论最大面波到时与实测最大面波到时偏差较大等方面。这些都对大连地震台精确测定面波震级带来影响。在此背景下，进行大连地震台面波震级校正具有极大意义。

为全面准确描述大连地震台面波震级的台基校正问题，我们按照不同震中距、不同震级、不同方位角分别进行讨论。

2 资料的选取与可靠性分析

2.1 面波震级试算

中国地震台网中心提供的试算的大连台面波震级台基校正模型，见表1。

表1 大连台面波震级台基校正模型

表1中，该模型提供了两种校正模型：一种为按照不同震中距分别加上相应的台基校正值；一种为不分震中距的台基统一校正值，即表1中最后一列。相应的标准差与地震数也列在表1中。

基于该模型，我们对1985年至2003年大连地震台共计1357次地震进行了面波震级台基校正试算。这1357次震例中，大连地震台单台测定面波震级大于国家台网面波震级的震例为161次，约占11.86%；等于国家台网面波震级的震例为190次，约占14.00%；小于国家台网面波震级的震例为1006次，约占74.13%。这与实际情况吻合，即大部分情况下，大连地震台单台测定面波震级小于国家台网面波震级。该1357次震例分布及偏差情况见图1-4。其中大连地震台单台测定面波震级大于国家台网面波震级的震例标示为方块；等于国家台网面波震级的震例标示为十字；小于国家台网面波震级的震例标示为圆点。

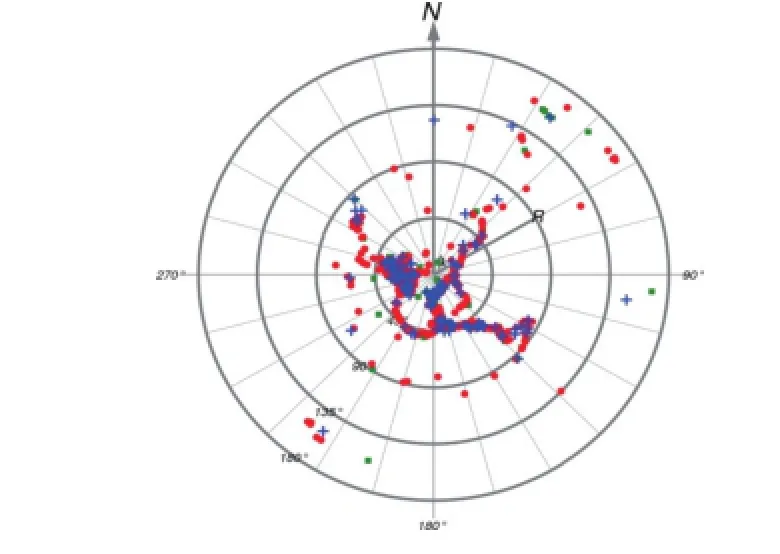
图1 全部试算震例分布Fig.1 All trial distribution of earthquake examples

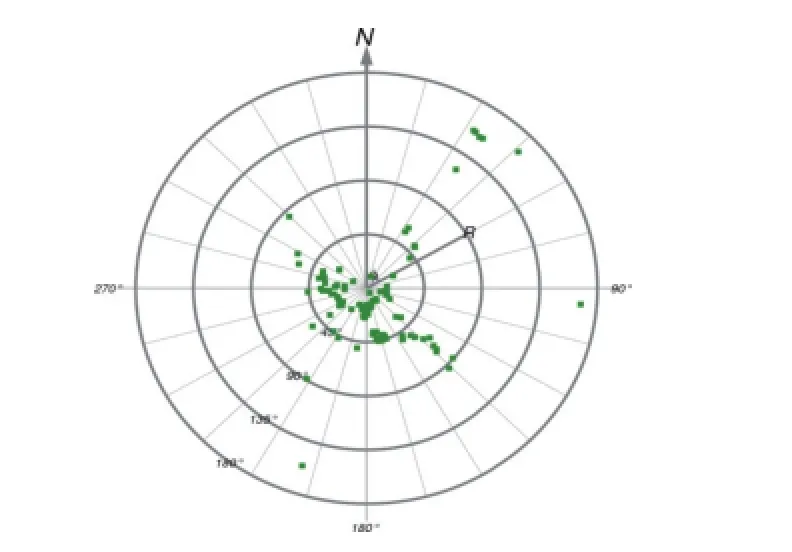
图2 大连地震台单台面波震级大于国家台网震级震例Fig.2 Earthquake examples of Dalian seismic station single surface wave magnitude greater than the national network magnitude

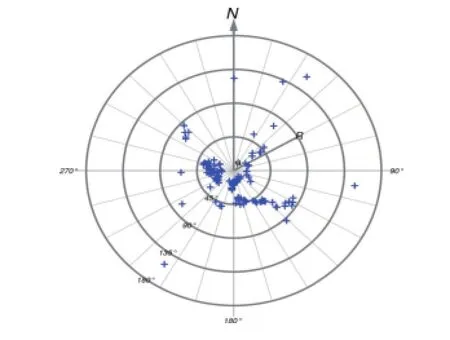
图3 大连地震台单台面波震级等于国家台网震级震例级震例Fig.3 Earthquake examples of Dalian seismic station single surface wave magnitude equivalent to the national network magnitude

图4 大连地震台单台面波震级小于国家台网震级震例Fig.4 Earthquake examples of Dalian seismic station single surface wave magnitude less than the national network magnitude

我们对每一次震例都分别按震中距、震级、方位角分别进行了讨论，按照不加台基校正值、加分震中距区间校正值、加总校正值分别计算了平均偏差和相应的标准差。

2.1.1 按震中距讨论

按震中距讨论和计算的结果，见表2。

由表2可知，对于30°以内的地震，大连地震台进行面波震级校正后的结果要优于未进行面波震级校正时的情况；而对于30°以上的地震，校正后结果则不如校正前的好；按照统一校正模型进行校正后的结果也优于未进行校正时的情况。亦即对于大连地震台，震中距较近的地震，按该模型进行校正的结果较为理想；震中距较远的地震，则不按照该模型进行校正为宜。按照统一校正模型进行校正的结果虽然优于未进行校正时的情况，但考虑到校正前后的样本中，30°以内地震在数量上居于绝对优势，因此该优化结果应认为仍是由震中距较近的地震贡献的比重较大。

对于标准差的分析则表明，优化后的各标准差呈现了较好的一致性，除130～180°区间的标准差为±0.38外，其它各结果均为±0.23和±0.24。这应当是统计样本过大时，标准差趋于常数造成的，换言之，该常数应在±0.23或±0.24左右。此外，新的标准差几乎全部为正数，属系统性偏差，是大连地震台面波震级绝大部分小于国家台网面波震级的必然结果。

2.1.2 按震级讨论

按照震级进行讨论时，我们分两种情况进行了讨论，分别为以国家台网震级为标准和以大连地震台单台实测震级为标准。

a.以国家台网震级为标准

以国家台网震级为标准，我们对每一个震级区间进行了分别讨论。由于小于MS3.9和大于MS8.0的地震数量较少，进行标准差分析时可能离散程度较大，因此在对这两个震级区间进行单独讨论后，我们还将其分别并入相邻的4级地震区间和7级地震区间进行了讨论，见表3a、3b、3c。

表2 按震中距讨论台基校正值

表3a 按国家台网震级讨论台基校正值

表3b 分震中距区间校正

表3c 统一校正值

由表3a、3b、3c可知，小于MS3.9的地震仅有一例，因此其标准差由泊松误差得出，且其离散程度较高，故不参与讨论。小于MS6.9的地震，加上台基校正值的结果明显优于不加台基校正值的结果；加统一校正值的结果略优于加分震中距区间校正值的结果。而MS7.0以上地震加台基校正值的结果并未得到显著优化；MS8.0以上地震加台基校正值的结果则劣于不加台基校正值的结果。

同时上三张图说明，MS7.9以下地震的平均偏差均为正数，即大连地震台单台震级小于国家台网震级，且有随着震级增大，这种差值逐步减小的统计规律，至MS8.0以上地震，大连地震台单台震级变得大于国家台网震级。这种统计规律和变化趋势在加上分震中距区间校正值和统一校正值时，也有类似的体现。

各结果的标准差相比于按震中距讨论时，MS6.9以下地震的标准差集中在±0.23至±0.25左右；MS7.0以上地震的标准差则集中在±0.26至±0.28左右，表现出较好的分区间一致性。考虑到MS7.0以上地震数量较少，因此该结果应仍为大样本讨论时，标准差趋于常数的必然结果。

b.以大连地震台单台震级为标准

我们以大连地震台实测震级为标准，采用和a中相同的分类方法，对问题进行了讨论，计算结果见表4。

表4a 按大连地震台单台震级讨论台基校正值

表4b 分震中距区间校正

表4c 统一校正值

与a中讨论情况相类似，以大连地震台单台震级为标准进行讨论时，MS5.9以下地震，即震级较小的地震，加上台基校正值的结果明显优于不加台基校正值的结果；加统一校正值的结果略优于加分震中距区间校正值的结果。而MS6.0以上地震加台基校正值的结果并未得到显著优化；MS7.0以上地震加台基校正值的结果则劣于不加台基校正值的结果。相比于a.讨论的情况，出现拐点变化的震级偏小了一级。

对于平均偏差符号的讨论，也同样出现了相似的变化。MS6.9以下地震的平均偏差均为正数，即大连地震台单台震级小于国家台网震级，且有随着震级增大，这种差值逐步减小的统计规律，至MS7.0以上地震，大连地震台单台震级变得大于国家台网震级。这种统计规律和变化趋势在加上分震中距区间校正值和统一校正值时，也同样有类似的体现。且这种情况的拐点震级同样比a讨论的情况偏小一级。

对于标准差的讨论，则呈现为：MS6.9以下地震的标准差集中在±0.21至±0.25左右；MS7.0以上地震的标准差则集中在±0.26至±0.29左右；MS3.9以下地震和MS8.0以上地震由于地震数量较少，离散度较大。标准差在整体上也表现出较好的分区间一致性。

2.1.3 按反方位角讨论

按照定义，方位角是台站相对于震中的方位角；反方位角是震中相对于台站的方位角。由于前者无讨论意义，因此仅讨论后者，即按反方位角进行讨论。

我们将反方位角按照每45°一个区间进行划分，计算结果见表5。

表5a 按反方位角讨论台基校正值

表5b 分震中距区间校正

表5c 统一校正值

由表5可知，除0～44°反方位角区间外，其余各区间也呈现了如前所述的形态，即加分震中距校正值的结果优于未加校正值的结果；加统一校正值的结果又优于加分震中距区间校正值的结果。除0～44°区间加统一校正值外，其余各平均偏差均为正数，仍体现出大连地震台单台震级小于国家台网震级的统计规律。各标准差则表现较为离散，但仍集中在±0.20至±0.31间，仍有趋于常数的态势。

3 结论与讨论

大连地震台面波震级加台基校正值试算统计规律如下：

（1）大连地震台单台实测面波震级通常小于国家台网面波震级；

（2）分震中距区间校正值结果优于不加校正值，而统一校正值结果优于分震中距区间校正值；

（3）30°震中距以内加校正值后优化效果明显，30°震中距以上加校正值后效果劣化；

（4）实测震级≤MS5.9时，加校正值后优化效果显著。实测震级＞MS6.0时，加校正值后未见显著优化，甚至出现劣化。如果以国家台网震级为标准，则该现象的拐点震级提高一级；

（5）大震级地震加校正值后平均偏差出现变号，亦即校正过度；

（6）除0～44°反方位角区间外，各反方位角区间加分震中距校正值后得到优化，加统一校正值则进一步优化；

无论何种统计方式，各标准差都趋于某一常数，应为大样本数量统计的必然结果。鉴于台基校正值与震级间的关系较为明显，今后的讨论工作应对大地震和中小地震区分讨论。

在大连地震台震级试算工作中，由于小地震、30°以内震中距地震所占比重较大，客观上加大了相应区间权重，直接影响了最终平均偏差和标准差。在进一步的工作中，应尽量平均分配震级、震中距、反方位角等讨论区间的地震个数。而对于特大地震面波震级，还应考虑震级饱和可能带来的影响。

［1］田文德，胡俊明.成都台数字地震仪测定震级偏差分析与矫正［J］. 四川地震，2012，（3）：20-23.

［2］包秀敏，马莉. 沈阳地震台大震速报震级差分析［J］. 防灾减灾学报，2013，（3）：63-67.

［3］苏梅艳，毛世榕. 桂林台大震速报震级偏差的分析［J］.华南地震，2013，（3）：92-98.

［4］傅盛国. 大连地震台面波震级偏差及其矫正［J］. 东北地震研究，1991，7（4）：73-79.

ANALYSIS AND CORRECTION ON SURFACE WAVE DISPERSION IN DALIAN SEISMIC STATION

LI Hui-qing，WANG Jiu-yang，ZHANG Xin-hang，YUAN Chao，CHENG Shao-yun

（Dalian Seismic Station，Liaoning Dalian 116012，China）

The China Earthquake Networks Center provides a trial of Dalian surface wave magnitude platform calibration model， based on the model， the 1985 to 2003 in Dalian seismic station total 1357 earthquakes of surface wave magnitude platform trial and error correction. For platform in Dalian seismic surface wave magnitude correction， according to the epicentral distance， different earthquake magnitude， range angle are discussed respectively.

magnitude deviation； magnitude correction； correction model

P315.3；P315.78

A DOI:10.13693/j.cnki.cn21-1573.2016.03.021

1674-8565（2016）03-0109-06

2016-06-29

2016-07-26

李慧卿（1986-）女，山西省大同市人，2010年毕业于沈阳师范大学，计算机科学与技术专业，本科，助理工程师，现主要从事地震监测工作。