基于反馈控制的高阶温度补偿带隙基准电路

2016-10-26王宇星

电子与封装 2016年9期

王宇星，吴　金

基于反馈控制的高阶温度补偿带隙基准电路

王宇星1，吴金2

（1.无锡科技职业学院，江苏无锡 214028；2.东南大学无锡分校，江苏无锡 214135）

提出了一种温度系数可配置的高阶非线性带隙基准补偿技术。利用偏置支路实现闭环负反馈，在提高PSRR的同时，控制电路内部管子的直流工作点对基准电路进行非线性高阶温度补偿。通过优化电路参数设计，进一步改善了温度系数并且提高了整个电路的工艺稳定性。基于CSMC 0.5 μm CMOS工艺的仿真结果表明，在-55～125℃温度范围内两种模式基准电压温度系数为1.24×10-6/℃和2.841×10-6/℃，并具有非常好的工艺稳定性。在低频范围内平均电源抑制比达到46.3dB和70.6dB以上。

带隙基准；温度系数；电源抑制比；工艺稳定性

1　引言

SOC系统集成对带隙电压基准IP电路提出了越来越高的要求。带隙基准就进行补偿和具有正负温度系数的电学量而言，可以分为电流模式带隙电压基准源［2］和电压模式带隙电压基准源［3］。现有的电压模带隙基准基于△VBE正温度系数（PTAT）电压与VBE负温度系数（IPTAT）线性补偿的原理［1～3］，一阶线性补偿后仍残留一定的温度系数，典型的温度系数为7×10-6/℃以上［4～6］，PSRR在33 dB左右，同时由于电路中电流镜失配造成PSRR指标难以提高。

本文设计一种负反馈偏置控制的带隙基准电路，通过基于W/L失配控制的参数设计，提出了一种基于电路工作状态点控制的温度系数补偿方法，实现了高阶温度补偿特性，在保持较高电源抑制比（PSRR）的基础上进一步提高了电路工艺实现的健壮性。以上结构对电压模和电流模带隙基准均能适用，满足了更广范围下对高性能基准的应用需要。

2　典型带隙电压基准电路

利用正负温度系数补偿原理实现的电压模带隙电压基准，其电路原型结构如图1所示。

图1　典型电压模带隙电压基准

图1中N为Q2与Q1管发射区面积之比，偏置支路中由电流镜的匹配控制得到A、B两点电位相等，在匹配电流严格相等的条件下，形成△VBE=VTlnN的经典PTAT偏置，由△VBE/R0定义的支路电流通过PMOS电流镜线性传递到输出支路，再经电阻RREF还原为PTAT电压，最后与负温度系数VBE电压串联叠加后得到基准输出，即：

通过调节N和RREF/R0电阻比值，控制正负温度系数近似相等，得到的基准温度系数为12×10-6/℃。由于非可控失配与非线性残余温度量的影响，一阶线性补偿基准的温度系数难以有效提高；同时PSRR仅为22 dB，若PMOS电流镜采用Cascode结构，PSRR提高到43 dB，但基准受电源噪声扰动的影响仍然较大。

电路中在A、B两点分别增加到GND的两个相同的并联电阻R1a=R1b，并在输出支路将Diode二极管去除只保留纯电阻输出，得到的电流模带隙基准突破了1.2 V固定输出的限制，可在较宽范围内变化，通过电阻分压实现多值基准输出的应用。

电流模与电压模基准在温度系数补偿的原理上本质相同，两者具有近似相当的温度系数，但由于具有低交流电阻的VBE电压箝位功能在输出级消失，电流模基准在相同的条件下其PSRR特性进一步退化。为保持对电源噪声扰动的抑制能力，改善PSRR性能，图2给出了采用电流镜结构实现电流匹配控制的电流模带隙基准电路，其输出为：

式中K为输出电流镜线性传输系数。△VBE/R0的PTAT电流VBE/R1a的CTAT（Complementary PTAT）电流耦合在一起通过PMOS电流镜传输到输出级，通过电阻R3转化为基准输出电压。电流模基准电路因输出支路仅含电阻负载，通过电阻分压可获得多值基准输出，弥补了电压模基准的不足。但是由于两种特性电流在电流镜中耦合使得电流镜的匹配难度较大，所以电流易失配，对基准输出电压产生较大影响。

图2　典型电流模带隙电压基准

3　反馈控制的带隙基准电路实现

3.1电路结构

为避免以上两种结构各自存在的缺陷，同时结合两种控制结构独特的优点，可采用如图3和图4所示的一种基于内部反馈环路控制的三路偏置结构，环路采用闭环反馈控制，避免了其随机失调难以控制的缺点，又显著提高了偏置电路的匹配和稳定性。应用于电压或电流模基准中，将有效改善电路的整体性能。

图3的电流模基准电路结构中，低压PMOS Cascode电流镜的高输出阻抗有利于改善PSRR特性；同时由PM7→NM3→NM1→PM4→PM7构成的闭环负反馈环路，可进一步抑制包括电源VDD噪声在内的各种扰动；利用PM7与PM4两同类型PMOS管VGS的箝位作用，得到VC0=VC1，两路电流镜支路的电流匹配特性得到保障。即使在电流模结构下，1.2 V基准所具有的PSRR其仿真结果达到87.6 dB，同时基准输出在不同工艺角下的最大偏差仅为26%，工艺健壮性得到有效保障。

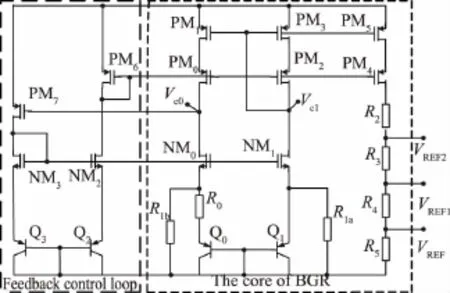
图3　电流模基准电路结构

实际上，电路内部还存在一条由PM7→NM3→NM0→PM7组成的正反馈环路，使得电路具有一定的自启动能力。电路结构中应使负反馈环路比正反馈环路具有更高的增益，以确保平衡条件下系统的稳定。由基准核心电路与自偏置回路共同构成一个环路控制结构。这种控制结构类似于运算放大器的作用，回路能有效提高整个基准电路PSRR。

图4　电压模基准电路结构

图4为同样原理应用在电压模基准电路结构中，同时采用分段高阶补偿来提高电路精度。Mn管并联在电阻Rn端，栅电位接基准或近似基准输出，选择其源端合适的电位使该管从低温段开始导通。由于低温起点的补偿在高温区同样起作用，因此必须协同配置补偿起始点，补偿量的大小以及一阶非对称补偿曲线的变化特性。由于VGSN的正温度特性与VTN的负温度特性，使得Mn管有效驱动电压呈正温度特性并占主导作用，Mn管电流导通后随温度上升而增加，流过Rn电阻电流的正温度系数减小而负温度系数增加，输出负温度特性加强，形成第一个极高峰值点。同时由于补偿管并联的分流作用，输出电压值降低，二阶补偿特性。由于Mn管栅压VGN及其温度特性在一定范围内可自由配置，当VGN下降到低于基准电压时，VGN负温度系数增加，Mn管电流的正温度系数下降，从而抑制了输出电压的降低。这意味着可通过配置VGSN电压选择合适的补偿起始点及其温度系数得到所需的二阶补偿特性，当补偿设定后，Mn管的温度负反馈控制更有利于温度特性的稳定。

在实际调制电路中，输出支路电流的大小会影响该支路三极管EB结的温度特性，因此，在优化电压模结构时，要综合输出支路电流大小、补偿电流大小，以及基于降低电流失配参数设计这三方面优化考虑。

3.2高阶温度补偿原理

根据VBE的非线性温度特性［2］：

式中VG0为0 K下硅材料的带隙电压，典型值为1.205 V，常温T0=300 K，γ、α分别为与三极管基区空穴迁移率和集电极电流指数温度系数相关的系数。带隙电压VG（T）的非线性温度系数可表示为［2］：

式中TC1（VG）=∂VG/∂T、TC2（VG）=∂2VG/∂T2分别为VG（T）的一阶与二阶温度系数，以上温度系数经计算均小于0的负温度系数。考虑到实际电路中Q0与Q1支路的电流失配，输出PTAT电压修正为：

式中m为电阻比与输出电流镜传输系数决定的比例常数，常温下热电压VT=KT/q=26 mV，K=IC1/IC0。当支路电流IC0（T）相对IC1（T）存在微小的失配△I（T）时，即IC0（T）/IC1（T）=1-△I（T）/IC1（T）。根据x→0时ln（1-x）≈x的近似关系，有：

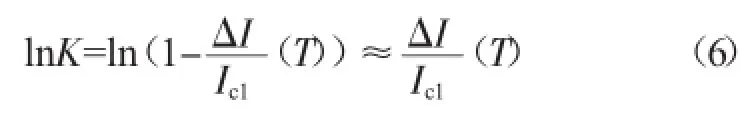
显然，lnK为PTAT电压中引入的非线性失调量。利用VPTAT中正的线性温度系数项补偿VBE中的负温度系数线性项，得到的一阶线性补偿基准中将仅存留VG的高阶负温度系数项、VBE中残留的非线性温度项VT（γ-α）ln（T/T0）、VPTAT中的lnK失调项，即：

如果控制上式中非线性失调项lnK的极性及大小以补偿基准中残余的高阶温度系数量，将可实现高阶温度系数的补偿效果。

3.3温度系数优化

VPTAT中的失调补偿量lnK应与高阶非线性剩余温度系数量相匹配，非线性失调在整个温区内的非均匀补偿作用，要求一阶补偿的非对称温度特性与之互补匹配，以使基于失配控制的高阶补偿后恢复温度曲线对称分布，最终得到最低的温度系数。

（1）（γ-α）VTln（T/T0）项中，γ=4-n，n为PN结发射区中载流子迁移率的温度指数系数，与衬底浓度及发射区浓度有关，变化范围为0.8～2，轻掺杂下n值较高。由于α=1-αR=1-TCRT0，其中TCR为电阻的一阶温度系数。对于正温度系数电阻，TCR＜0，电阻指数温度系数α＜0，γ-a＞0；只有TCR＜0的负温度电阻值才能有效提高α数值。对于负温度系数电阻，由于γmin≈2，只有在αR＜-1时，才有可能实现γ-a＜0，当γ提高或αR负温度系数不足时，只能出现γ-a＞0的状态。因此，采用负温度系数较高的多晶电阻以减小γ-a值，能在一定程度上降低一阶补偿电压基准中残余的非线性温度系数。由于无法通过γ-a=0的控制方式彻底消除以上非线性温度系数，只有利用失配的高阶补偿控制。

（2）对于带隙电压VG的非线性负温度系数来说，一阶和二阶负温度系数为：

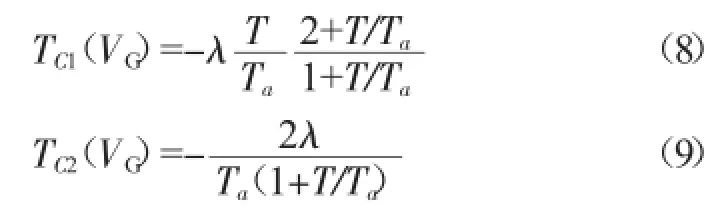
式中λ=0.473 mV/K，参考温度Ta=638 K。表1给出了-55～125℃全温区范围内VG（T）一阶与两阶负温度系数的计算结果。TC1（VG）近似具有常系数性质，可参与一阶线性补偿；而TC2（VG）的数值则随温度增加而下降，成为高阶非线性补偿的对象。

A中非线性温度项在高低温区下的温度系数极性不同，低温区为正温度系数，进入高温区域则转变为负温度系数。非对称一阶补偿适当增加负温度系数量，可进一步补偿A中非线性项在低温区内的正温度系数，使低温区温度系数降低；而在高温区内A中的非线性负温度系数与VG（T）的负温度系数均可利用非线性失配电流的正温度系数进行补偿，降低高温区温度系数，最终实现在全温区范围内基准温度系数的高阶补偿特性。

表1　Vg（T）的两阶非线性温度系数表

以上理论分析表明，通常条件下电流镜失配对高精度基准产生不良影响，但在电流镜失配数值与极性精确可控的条件下，工作点失配产生的非线性电流量可成为实现高阶补偿控制的有效方法。

根据Pelgrom简化模型［7］，在MOS管面积不变的条件下，通过增加MOS管的有效面积可有效控制失配大小；此外，将电流镜中的一个MOS管分裂为若干相同子单元的并联实现方式，同样有助于控制电流镜的自身失配水平［8］。在由电流方程推导出的电流镜偏差公式中［1,7,8］，电流相同时W和L的选取应优化其过驱动电压，以此提高电流镜的电流匹配精度。电路参数的优化选取可以控制匹配精度，同样也能控制失配的精度。

参数设计优化中，NM0与NM1、NM3与NM2的宽长比分别相同；PMOS电流镜中的PM0～PM2以及PM3～PM5的宽长比分别相同；为避免短沟道效应，可将电流镜MOS管的沟道长度取为工艺最小特征尺寸的4倍；三极管Q0、Q1、Q2、Q3的面积之比为8∶1∶1∶1。进一步调节电阻R1以及PM6管宽长比，即可有效降低输出电压的温度系数。当PM6管宽长比增大时，PM3～PM5管漏极电位升高，当进入线性区临界点后将使Cascode电流镜输出阻抗降低，导致PSRR性能退化。因此，输出基准的PSRR特性与温度系数之间存在一定的制约关系。表2、3给出了电路主要参数经迭代调整后最终的优化设计值，在此条件下，基准温度系数和直流低频PSRR均得到显著的改善和提高。

表2　电流模基准设计参数

表3　电压模基准设计参数

4　系统验证及分析

采用CSMC 0.5 μm CMOS工艺并基于Cadence Spectre仿真环境，对以上改进电路的输出基准特性进行了全面验证。设置输出电阻比例，可以得到任意低值的输出基准电压。仿真选择的3种基准输出电压分别为120 mV、1 V和1.25 V。

4.1基准的线性电源调节及PSRR特性

图5分别给出了两种模式电路在给定的电源电压VDD范围内电流模三路输出基准的线性电压调节特性以及动态PSRR特性。图6（a）电流模基准的最小工作电压为2.1 V，在电源电压线性变化范围内的基准变化量仅为0.2 mV，其PSRR绝对值为46.3 dB。图6（b）电压模基准电压源在低频100 Hz时的电源抑制达到了-70.6 dB，10 kHz时为-63.36 dB。

图5　输出基准的电源线性调节特性

基于反馈控制的高阶补偿电路存在温度系数与PSRR的相互制约关系。图7给出了电流模基准TT典型工艺条件下不同温度系数与PSRR性能的关系数据，以其中的120 mV基准输出为例，当温度系数调节到最低的1.24×10-6/℃时，VREF波动为0.846 mV，PSRR大于66 dB，当温度系数增大到6.8×10-6/℃时，VREF波动降为0.05 mV，PSRR提高到99.7 dB。这表明，当用于高阶补偿的失配量增大时，虽然温度特性得到改善，但引起PSRR特性的下降，两者之间需要适当折中平衡。

图6　电流模输出基准的PSRR特性

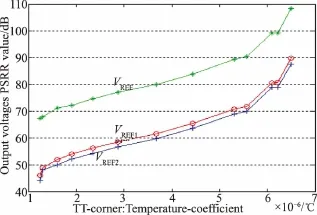
图7　输出电压温度系数与PSRR特性的关系曲线

4.2基准电压温度系数特性

各种高阶补偿基准在TT工艺条件均能获得近似完美的补偿效果，在-55～125℃温度范围内，图8给出了VREF=120 mV输出电压的温度特性曲线。

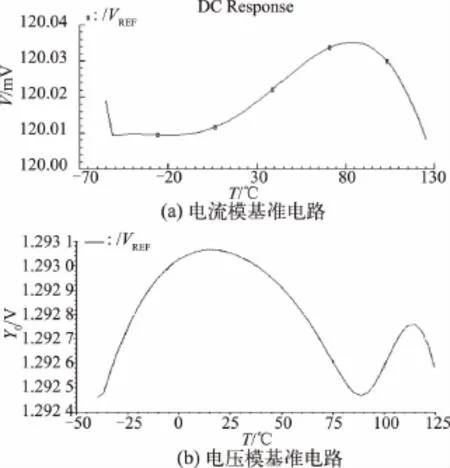
图8　VREF温度特性曲线

在已有的各类高阶补偿结构中，均无法克服工艺漂移对系统性能的严重影响，基准温度系数的最大漂移达到数十倍之巨，其性能和工艺稳定性甚至还不如相应的一阶线性补偿基准，严重限制了高阶补偿技术的应用。

由于采用内部负反馈及基于匹配状态的控制，论文提出的电路本质为以一阶补偿结构性质以获得高阶补偿的效果，因此工艺健壮性相对于其他类型的高阶补偿结构得到明显的提高。图8（a）在给定的-55～125℃全温区范围内，对TT、SS、SF、FS、FF 5种典型工艺角下的基准温度特性进行的仿真验证，其温度系数分别为1.24×10-6/℃、8.61×10-6/℃、8.48×10-6/℃、5.07× 10-6/℃和12.6×10-6/℃，最大工艺漂移下的温度系数变化可控制在10倍以内。图8（b）TT模型下补偿后输出电压的纹波幅度仅为0.6061 mV，输出精度值为2.841×10-6/℃，温度系数减小很多。

综上所述，控制电路结构的失配量可实现补偿性质在一级到两阶之间的变化，当电路性质向一阶补偿转化时，虽然温度系数略有损失，却换来PSRR和工艺健壮性的大幅度提升。由此，根据实际应用需求，合理选择失配控制，能够有效改善基准电路的总体综合性能，有效提升可调节高阶补偿基准的实用价值。

5　结论

基于 CSMC 0.5 μm CMOS工艺的 Cadence Spectre仿真结果，验证了电路性能符合理论预期。表4给出了文中设计电路与相关文献电压基准源的比较。同样的温度系数下，本文中的PSRR比文献［6］中提出的电路在相同的输出电压和温度系数下PSRR要高20 dB以上；在同样的温度范围内最优温度系数可降低5×10-6/℃以上，而与文献［4］提出的高阶补偿结构相比，本文提出的电路结构更为简单，并且温度系数同比降低了8.7×10-6/℃。

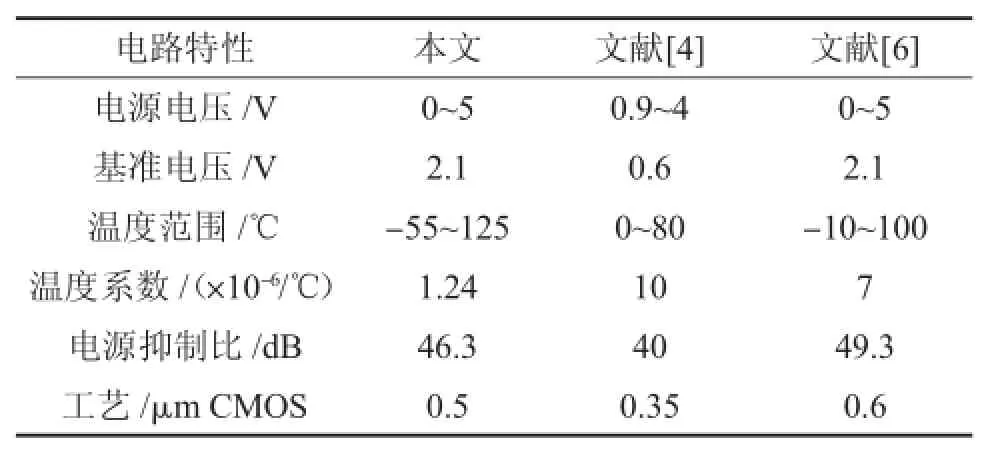
表4　本电路电流模基准与相关文献电压基准源性能比较

本文提出的基于电路工作状态控制的带隙基准高阶温度补偿方法，可实现极低的温度系数，达到高阶补偿的目的；同时状态控制电路可以不仅在稳态时提供闭环负反馈，极大地提高了输出基准电压的PSRR特性，而且使得电路具有自启动能力。该电路结构能够根据应用的不同在一定范围内灵活配置基准电压的大小，实现多路输出。通过失配参数的精确控制，基准的温度系数、PSRR和工艺健壮性等综合性能能够得到较好的平衡，电路综合性能明显改善。

［1］Paul R Gray,Paul J Hurst,Stephen H Lewis.ANALYSIS AND DESIGN OF ANANLOG INTEGRATED CIRCUITS［M］.Fourth Edition,BeiJing：High Education Press,2005：317-327.

［2］Yan Li,Jin Wu,Zhiqi Huang.A Sub-1ppm/℃high-order curvature-compensatedbandgapreference［J］.IEEEAPCCAS, Nov.30,2008 Page（s）：1204-1207.

［3］Leung K N,Mok K T.A sub-1-V 15ppm/℃ CMOS bandgap voltage reference without requiring low threshold voltage device［J］.IEEE J Solid-State Circuits,2002,37（4）：526-530.

［4］De Vita,G,and Iannaccone,G.A sub-1-V,10 ppm/8℃, nanopowervoltagereferencegenerator［J］.IEEEJ Solid-State Circuits,2007,42（7）：1536-1542.

［5］Huang shizhen,Lin Wei,Chen Wangsheng.A Design of HighPSRRCMOSVoltageReferenceBasedon Subthreshold MOSFETs［J］.IEEE Conference on Industrial Electronics and Applications,June 2008.

［6］Dongfang Cheng,Xiaohui Li,Jue Zhang.A Dual-Output Voltage Reference for High-Accuracy Pipelined ADC［J］. IEEE,ICEPT-HDP,2008.

［7］M J M Pelgrom,A C J Duinmaiger,A P G Welbers. Matching properties of MOS transistors for precision analog design［J］.IEEE J Solid-State Circuits,1989,24：1433-1439.

［8］Patrick G Drennan,Colin C McAndrew.Understanding MOSFETMismatchforAnalogDesign［J］.IEEEJ Solid-State Circuits,2003,38.

A High Order Temperature Compensation Bandgap Voltage Reference Based on the Feedback Controlling

WANG Yuxing1,WU Jin2
（1.Wuxi College of science and technology，Wuxi 214028，China；2.Southeast University WuXi Campus，Wuxi 214135，China）

A new nonlinear temperature-compensation method which can reduce the temperature coefficient effectively by controlling the DC operating points of the critical nodes in circuits has been proposed in this paper.Based on this method,the tempreture-coefficient of the BGR circuit can be configured.Using negative feedback loop improve the PSRR and optimization method of the parameters further to improve the temperature coefficient and reduce the process sensibility of the whole voltage reference circuits.Simulated in CSMC0.5μm HVCMOSprocess,ithasa temperature coefficientinthe-55℃to 125℃range of 1.24×10-6/℃and 2.841×10-6/℃ at TT corner,also the temperature coefficient has smaller changes variers from other different corners.At low frequncy range its average PSRR value is higer than 46.3 dB and 70.6 dB.

bandgap reference；temperature coefficient；PSRR；process stability