稀疏阈值的超分辨率图像重建
2016-10-26王新华郝建坤
何 阳,黄 玮,王新华,郝建坤
(1.中国科学院 长春光学精密机械与物理研究所 应用光学国家重点实验室,吉林 长春 130033;2.中国科学院大学,北京 100049)
稀疏阈值的超分辨率图像重建
何阳1,2,黄玮1*,王新华1,郝建坤1,2
(1.中国科学院 长春光学精密机械与物理研究所 应用光学国家重点实验室,吉林 长春 130033;2.中国科学院大学,北京 100049)
为了解决基于字典学习的超分辨重构算法耗时过长的问题,提出了基于稀疏阈值模型的图像超分辨率重建方法。首先,将联合字典理论与图像块稀疏阈值方法相结合,训练得到高、低分辨率过完备图像字典对。接着,通过稀疏阈值OMP算法对图像特征块进行稀疏表示。然后,通过高分辨率字典重构出初始的超分辨图像。最后,通过改进迭代反投影算法对初始的超分辨图像进行全局优化,从而进一步提高图像重构质量。实验结果表明,超分辨图像重构平均峰值信噪比(PSNR)为30.1 dB,平均结构自相似度(SSIM)为0.937 9,平均计算时间为10.2 s。有效提高了超分辨重构的速度,改善了重构高分辨图像的质量。
超分辨率;稀疏阈值;字典学习;迭代反投影算法
1 引 言
图像的超分辨率重构[1]一直是数字图像处理的热点之一。超分辨率图像重构可以突破传统光学上物理极限分辨率的限制,实现对图像高分辨率重建。在光学成像系统中,由于受到硬件和环境的制约,获取高分辨率图像比较困难而且成本较高,利用软件实现高分辨率图像重构是一种低成本的解决方法。
按图像输入方式对图像超分辨重建进行分类,一般可以分为多帧图像输入和单帧图像输入超分辨图像重构两种类型。其中,多帧图像序列超分辨重构是对低分辨率图像序列进行图像匹配和图像融合,从而恢复图像的细节信息。在图像匹配不准的情况下,重构得到的图像质量会急速下降。对于单帧图像输入的超分辨,主要是通过基于学习的方法,从训练样本中提取所需的高频信息,从而对输入的单帧图像进行超分辨重构[2-4]。目前,实现超分辨的主要方法有插值、基于多帧重构和基于学习3种。插值主要包括双线性插值、双三次插值和邻近插值等;基于重建的方法[5-6]有凸集投影法、贝叶斯后验概率法、迭代反投影法和正则化方法等;基于学习的方法主要包括基于例子学习、基于字典学习方法等。图像插值法理论模型简单,计算量小,程序处理速度快,但是所能恢复图像细节信息少,重建得到的图像质量不高;基于重建的方法是通过建立数学模型重建图像,能在一定程度恢复出图像细节,但是由于图像所包含的信息较多,很难采用一种数学模型对其进行良好的描述,在图像放大倍率较大的情况下,重建图像质量下降明显。目前大多数学者主要是对基于学习的重构算法进行研究,该方法能够克服上述缺点,通过学习高低分辨率图像之间的关系来重建图像。基于学习的方法相对于插值法和重构方法能够恢复出更多的细节信息。
基于学习方法的基本思想是捕捉高低分辨率图像块之间的共同特性,从而进行图像的高分辨率恢复重构。Freeman[3,7]提出的基于例子的重构算法,是最先利用图像间的约束进行图像的恢复重构的算法。Sun等人[8]在Freeman算法的基础上进行改进,通过使用原始图像轮廓的先验性条件的方法来消除图像边缘的模糊,提高图像的质量。Yang等人[4]提出了基于稀疏表示的图像超分辨率重构算法,对图像进行稀疏表示,不但能够保证重建图像所需的先验性条件,而且能够在重建过程中降低数据计算量。在此之后,国内外学者提出了诸多基于稀疏表示的超分辨率重建的改进算法[9-11]。
本文在Yang提出的联合字典训练理论的基础上,改进其稀疏表示算法和重构优化算法,实现高分辨率重构。对单帧低分辨率图像输入,能够快速对其进行超分辨率图像重构。
2 稀疏表示基本原理
2.1基本理论框架
单幅图像的超分辨重构问题:给定一幅低分辨率的图像Y,恢复同一场景的高分辨率像X。观测得到的低分辨率Y是高分辨率图像X经过了降采样和模糊之后得到的图像,图像获取模型可以表示为:
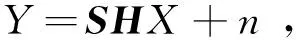
(1)
式中,S是降采样矩阵,H是模糊矩阵,n表示高斯白噪声。超分辨问题可以描述为:
(2)
给定一个低分辨率图像,基于不同的约束条件可以重构恢复很多高分辨率图像。Yang等人提出了基于图像稀疏先验性条件来进行图像超分辨率重建。
D∈Rn×K表示为一个具有K个元素(K>n)的过完备字典,对于信号X∈Rn可以利用过完备字典D的稀疏线性组合表示。
(3)
式中,X表示高分辨率图像,Y表示低分辨率图像(或者提取出来的低分辨率图像特征)。通过少数对X的线性观测能够得到Y:
(4)
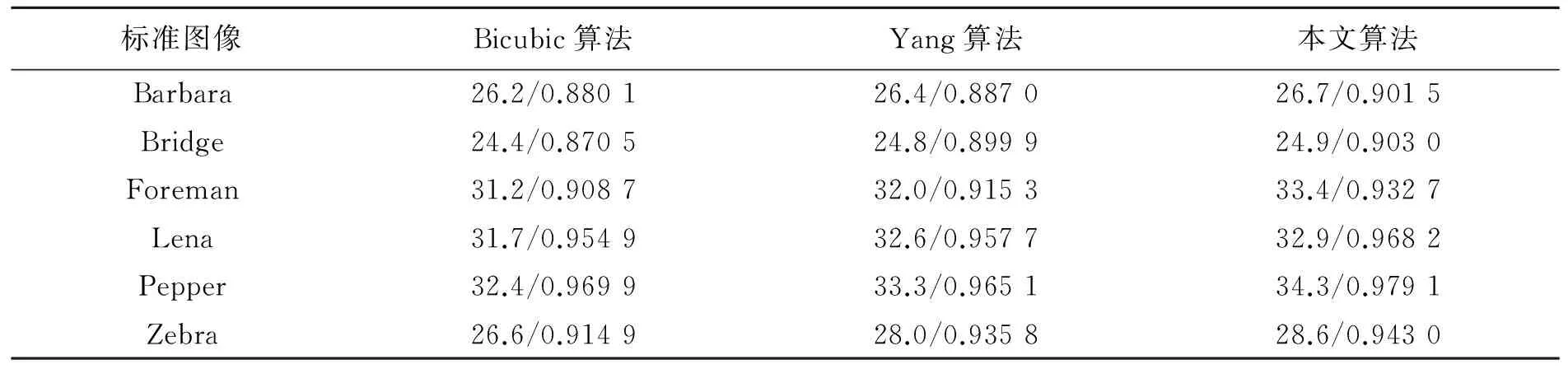
式中,L∈Rk×n(k 设图像X的第i个图像块用过完备字典Dh∈Rm×K进行表示: (5) 式中,图像块中的像素数用m来表示,K表示过完备字典Dh中的原子数,qi的l0范数表示向量中非零元素的个数。和为对应高低分辨率图像块对,由式(1)可以得到: (6) 图像对和有相同的稀疏系数,因此可以通过求解低分辨率图像块的稀疏表示,然后通过式(5)求解相应的高分辨率图像块。 2.2联合字典学习 图像的稀疏表示的一个关键问题是找到过完备字典,对于给定的一系列高低分辨率图像对{Xh,Xl}训练得到,从待训练的图像数据中提取出高低分辨率的图像块{和}训练得到过完备字典。其中Dh表示的用于高分辨率图像块稀疏的过完备字典,而与此对应的Dl是低分辨率图像块稀疏表示的过完备字典,训练得到的Dh和Dl用于图像的超分辨重构。从一系列训练样本X={x1,x2,…,xn}学习得到过完备字典。可以表示为如下公式: (7) 式中,Z的L1范数是为了保证稀疏性,D的行的L2范数的限制条件是去除图片尺寸的模糊性。式(7)在文献[15]中有着详细而广泛的研究。 对于高低分辨率的图像块对P={Xh,Yl},希望通过相应的字典,高低分辨率图像块有着相同的稀疏表示。其中高分辨率图像块和低分辨率图像块单独的稀疏表示问题可以进行如下表示: (8) (9) 考虑到希望最后有着相同的稀疏表示,将式(8)和式(9)的目标函数相结合,强制使得高低分辨率图像块有着相同的稀疏表示: (10) 式中,N和M是高分辨率和低分辨率图像块表示为向量形式的长度。 可以将式(10)进行简化得到: (11) 其中: (12) 在图像重建过程中,通过对提取的低分辨率图像的细节数据进行处理,能够得到更好的重建结果。有多种滤波器可以用于提取低分辨率图像块Yl中的特征,Freeman[5]使用高频滤波器提取低分辨率图像块的边缘信息;Sun等人[8]使用高斯微分滤波器提取图像的轮廓信息;Chang等人[16]使用的是一阶和二阶微分滤波器提取图像特征。本文算法对进行特征提取,使用的是4个一维滤波器: (13) 与图像进行卷积就能得到4个图像细节特征矩阵。 3.1稀疏阈值OMP算法 图像块的稀疏表示在图像超分辨重构的过程中有着重要的影响,稀疏表示会影响到程序的运行速度和重构图像的质量。本文通过加入稀疏阈值条件的OMP方法对图像块进行稀疏表示,即 (14) 式中,q为图像块的稀疏表示,λ表示约束项系数,λ∈(0,+∞)。在本文中,‖q‖1表示q的L1范数。 稀疏度阈值t的设定会影响到程序的运行速度和最后重构图像PSNR[17],在实验中综合考虑将每个图像块稀疏阈值t设定为6。 学习得到字典在后续的超分辨重构过程中起着很重要的作用,不同的字典最后可能获得不同的重构图像质量。在进行字典学习的过程中加入稀疏表示阈值,即在式(11)基础上加入额外限制条件‖Z‖0≤Threshold,表示为: (15) 为了保证高低分辨率图像对具有相近的稀疏系数,采用式(15)方法训练Dh和Dl字典对。采用交替迭代的方法对式(15)进行求解,即先对字典对Dc,进行固定,求解在此字典上训练样本的稀疏表示Z;然后再固定稀疏表示Z,求解字典对Dc。其具体步骤如下: 步骤1:采用随机高斯矩阵初始化字典对Dc; 步骤2:固定字典对Dc,计算稀疏表示Z;优化式(14)问题,即: (16) 解决式(16)问题,通过上述的稀疏阈值OMP算法进行求解; 步骤3:固定稀疏表示Z,对字典Dc更新;优化式(15)问题,即: (17) 采用类似K-SVD[4]的算法进行求解; 步骤4:判定循环终止条件,否则返回步骤2继续求解。 3.2改进迭代反投影 通过低分辨率训练字典得到了低分辨率图像块的稀疏表示qi,高分辨率高频图像块可以求得xi=Dhqi,由重建得到图像块高频信息集合{xi}与从Bicubic插值放大图像块提取的低频信息集合进行叠加得到高分辨率图像Xh可能会由于重建过程中引入的噪声导致不满足Y=SHX,对Xh进行投影迭代优化,将初始高分辨率图像设定X0。 (18) 对重构图像采用迭代反投影算法[18],求解式(18)的优化问题采用改进的迭代反投影算法,其中更新迭代为: (19) (20) 式中,α、β是系数,为了使得算法具有收敛性,其取值范围需要满足一定条件。Y=SHX=RX,将R分解R=C-T,其中C是正定且易于求逆的矩阵。α、β系数的取值范围需要满足0<α<2,0<β<2α/λmax条件,λmax表示C-1R的最大特征值[19]。Y表示低分辨率图像,R=SH为降质矩阵,↑s表示放大倍率因子,p是反投影算子,本文采用的是高斯滤波器。 本节介绍了基于稀疏阈值OMP超分辨算法和改进的迭代反投影算法。图像超分辨率重构的基本思路是,利用训练得到的高低分辨率过完备Dh和Dl字典对,通过稀疏阈值算法对图像特征块进行稀疏表示,然后通过高分辨率字典估计出初始超分辨图像。最后通过改进迭代反投影算法对初始超分辨图像进行全局优化,进一步提高图像成像质量。超分辨率图像重构算法基本步骤如下: 步骤2:对每个图像块利用得到的训练字典Dl,采用上述稀疏阈值OMP算法求解式(14)得到图像块的稀疏表示{qi}; 步骤3:利用训练得到的高分辨率字典Dh求得高分辨率图像块xi=Dhqi,由{xi}和从Bicubic插值图像Xl中提取得到的图像低频信息构成初始高分辨率图像Xh; 步骤4:使用改进的迭代反投影算法对Xh进行优化得到X*。 本程序采用Matlab2011b编写,硬件环境为:CPU为Interl(R) Core(TM)2 Duo;主频2.79 GHz;内存2.99 G。随机选取文献[4]图像库中的10万对高、低分辨率图像特征块将其作为字典的训练样本。其中,图像块大小是3×3,图像块间采取最大重叠方式。训练的字典大小为1 024,即Dh∈R9×1024,Dl∈R36×1024。字典训练时,迭代次数设定为40(终止条件)。其中实验具体参数:λ=0.18,α=1.67,β=3.31。客观上,重建图像质量采用峰值信噪比(PSNR)和图像结构自相似度(SSIM)[20]两种方式进行评价。实验选取图像处理中的标准图像库中的图像进行测试。 表1是标准图像库中通过3种方法恢复重构结果的PSNR和SSIM的比较结果。从表1可以看出,在PSNR和SSIM两方面,相对于Bicubic算法和Yang算法的结果,本文算法得到的PSNR和SSIM数值都是最高的。通过客观评价方式对PSNR和SSIM的数值进行比较,本文的平均PSNR为30.1 dB,平均SSIM为0.937 9,相对于Bicubic算法平均PSNR提高了1.4 dB,平均SSIM提高了0.021 4,相对于Yang算法平均PSNR提高了0.6 dB,平均SSIM提高了0.011 1。 表1 3种算法重构图像峰值信噪比(PSNR/dB)和结构自相似度(SSIM)对比 图1 3倍超分辨率Lena图像重建结果 Fig.1 Results of 3×super-resolultion reconstruction for image of Lena 图1和图2全局低分辨率图像像素值为170×170,恢复出的高分辨率图像像素为510×510,其中截取了Pepper图像中的局部图像进行表示,局部低分辨率图像大小45×45,高分辨率图像大小为135×135。观测图1,3种算法在图像平滑区域所恢复得到的效果区别不大,在细节恢复方面,Bicubic算法较差,而Yang和本文算法恢复的较好。从图1中的人物面部对比可以看到,Yang算法相对于本文算法将面部信息处理得更加平滑;视觉效果上,相比于Yang算法,本文算法在图像平滑区域上的处理与原始图像较为一致;在图像亮度方面,Bicubic算法与原始图像相比偏暗,Yang算法重建得到的图像偏亮,与原始高分辨率图像相差较大,本文算法得到的图像在亮度方面与原始图像保持较为一致。观测图2,Bicubic插值所得到的图像直观视觉上较模糊,而Yang算法和本文算法视觉上较清晰。在图像的平滑区域,图像的细节信息较少,3种算法恢复出的结果都较为一致。在图2中红框中,原始图像中下面有两个小白点,Yang算法中基本上观测不到第二次小白点这一细节信息,在Bicubic算法和本文算法中都能观测到相应的小白点,本文算法中的第二个小白点信息相对于Bicubic算法清晰。对比Yang算法和本文算法的图像,在Pepper图像的重构上,Yang算法重构得到的图像有着一条明显的竖直白线,而本文算法重构图像与原始图像较为一致。 通过图像库中的6幅图像进行超分辨重构,计算平均重构时间。将本文提出的算法和Yang算法进行比较,Yang算法在重构过程中需要427.5 s,本文算法重构时间为10.2 s,本文算法相对于Yang算法,在运行速度上有明显提高,提速近42倍。 本文在Yang联合字典学习理论的基础上,通过对图像块稀疏表示算法和迭代反投影算法的改进,实现了超分辨图像的快速重建。实验结果表明,本文方法与Bicubic插值方法相比,视觉效果方面有很大提高;与Yang 算法相比,PSNR方面平均提高了0.60 dB,在结构自相似度方面平均提高了0.011 1。在处理速度上,相对于Yang的算法,运行速度提高42倍。 [1]KANG M,CHAUDHURIS. Super-resolution image reconstruction[J].IEEE,2003,20(3):1920-1935.. [2]彭真明,景亮,何艳敏,等.基于多尺度稀疏字典的多聚焦图像超分辨融合[J].光学 精密工程,2014,22(1):169-176. PENG ZH M,JING L,HE Y M,etal.. Superresolution fusion of multi-focus image based on multiscale sparse dictionary[J].Opt.PrecisionEng.,2014,22(1):169-176.(in Chinese) [3]FREEMAN W T,PASZTOR E C,CARMICHAEL O T. Learning low-level vision," IJCV[J].J.ComputerVision,2000,40:25-47. [4]YANG J,WRIGHT J,HUANG T,etal.. Image super-resolution via sparse representation[J].IEEE,2010,19(11):2861-2873. [5]陈健,高慧斌,王伟国,等.超分辨率复原方法相关原理研究[J].中国光学,2014,7(6):897-910. CHEN J,GAO H B,WANG W G,etal.. Correlation theory of super-resolution restoration method[J].ChineseOptics,2014,7(6):897-910. [6]张振东,陈健,王伟国,等.基于SSIM_NCCDFT的超分辨率复原评价方法研究[J].液晶与显示,2015,30(4):713-721. ZHANG ZH D,CHEN J,WANG W G,etal.. Evaluation method of super-resolution restoration based on SSIM_NCCDFT[J].ChineseJ.LiquidCrystalsandDisplays,2015,30(4):713-721.(in Chinese) [7]FREEMAN W T,JONES T R,PASZTOR E C. Example-based super-resolution[J].ComputerGraphics&ApplicationsIEEE,2002,22(2):56-65. [8]SUN J,ZHENG N,TAO H,etal.. Image hallucination with primal sketch priors[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE,In Madison,USA,June 18-20,2003:729-736. [9]邓承志,田伟,汪胜前,等.近似稀疏正则化的红外图像超分辨率重建[J].光学 精密工程,2014,22(6):1648-1654. DENG CH ZH,TIAN W,WANG SH Q,etal.. Super-resolution reconstruction of approximate sparsity regularized infrared images[J].Opt.PrecisionEng.,2014,22(6):1648-1654.(in Chinese) [10]TANG Y,YUAN Y,YAN P K ,etal.. Greedy regression in sparse coding sparse for single-image super-resolution[J].J.Vis.Commum.ImageR,2013,24(2):148-159. [11]邓建青,刘晶红,刘铁军.基于DSP系统的超分辨率图像重建技术研究[J].液晶与显示,2012,27(1):114-120. DENG J Q,LIU J H,LIU T J. Super-resolution image reconstruction technology based on DSP system[J].ChineseJ.LiquidCrystalsandDisplays,2012,27(1):114-120.(in Chinese) [12]HE X,NIYOGI P. Locality preserving projections[J].AdvancesinNeuralInformationProcessingSystem,2004,45(1):186-197. [13]DONOHO D L. Compressed sensing[J].InformationTheoryIEEETransactionson,2006,52(4):1289-1306. [14]CANDES E,ROMBERG J. Sparsity and incoherence in compressive sampling[J].InverseProblems,2006,23(3):969-985. [15]LEE H,BATTLE A,RAINA R,etal.. Efficient sparse coding algorithms[J].Nips,2007:721-728. [16]CHANG H,YEUNG D Y,XIONG Y M. Super-resolution through neighbor embedding[J].IEEEConferenceonComputerVision&PatterRecognition,2004,1:275-282 [17]WANG J,ZHU S,GONG Y. Resolution enhancement based on learning the sparse association of image patches[J].PatternRecognitionLetters,2010,31(1):1-10. [18]WANG S,HUANG T Z,LIU J,etal.. An alternating iterative algorithm for image deblurring and denoisingproblems[J].CommunicationsinNonlinearScience&NumericalSimulation,2014,19(3):617-626. [19]BIOUCAS-DIAS J M,FIGUEIREDO M A T. A new twist:two-step iterative shrinkage/thresholding algorithms for image restoration[J].IEEETransactionsonImageProcessing,2007,16(12):2992-3004. [20]BRUNET D,VRSCAY E R,WANG Z. On the mathematical properties of the structural similarity index[J].IEEETransactiononImageProcessing,2012,21(4):1488-1499. Super-resolution image reconstruction based on sparse threshold HE Yang1,2, HUANG Wei1*, WANG Xin-hua1, HAO Jian-kun1,2 (1.State Key Laboratory of Applied Optics,Changchun Institute of Optics,Fine MechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China;2.UniversityofChineseAcademyofSciences,Beijing100049,China)*Correspondingauthor,E-mail:huangw@ciomp.ac.cn In order to solve the problem of the time consuming of the super-resolution reconstruction algorithm based on dictionary learning, a method of super-resolution image reconstruction based on sparse threshold model is proposed. First of all, the over-complete dictionary couple based on the theory of joint dictionary by method of sparse threshold is obtained. And then, the sparse representation of feature block image is represented by sparse threshold OMP algorithm. Then, the initial super-resolution image is reconstructed by the high resolution dictionary. Finally, the global optimization of the initial super-resolution image is improved by the modified iterative back projection algorithm, which can improve the quality of reconstructed image. The experimental results show that the average peak signal to noise ratio(PSNR) is 30.1 dB; the average structure self-similarity(SSIM) is 0.937 9; the average computation time is 10.2 s. This method can improve not only the speed of super-resolution reconstruction, but also the quality of reconstructed high resolution images. super resolution;sparse threshold;dictionary learning;iterative inverse projection algorithm 2016-05-11; 2016-06-13 应用光学国家重点实验室自主基金资助项目(No.Y4223FQ141) 2095-1531(2016)05-0532-08 TP394.1; TH691.9 Adoi:10.3788/CO.20160905.0532 何阳(1990—),男,湖南常德人,硕士研究生,2013年于华中科技大学获得学士学位,主要从事超分辨图像重建方面的研究。E-mail:merelyyang@163.com 黄玮(1965—),男,吉林长春人,研究员,博士生导师,主要从事光学系统设计方面的研究。E-mail:huangw@ciomp.ac.cn Supported by Foundation Project of State Key Laboratory of Applied Optics of China(No.Y4223FQ141)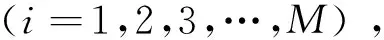
3 基于稀疏阈值的超分辨图像重构
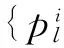
4 实验测试与结果

5 结 论


