旋转帽罩表面积冰甩脱位置的数值模拟

傅　亮，陈　勇，王安正

（上海交通大学机械与动力工程学院，上海200240）

旋转帽罩表面积冰甩脱位置的数值模拟

傅亮，陈勇，王安正

（上海交通大学机械与动力工程学院，上海200240）

为了更好地理解旋转帽罩表面积冰的甩脱机理和过程，采用水杯法在万能试验机上分别测得积冰/铝板界面黏附强度值和积冰内部拉伸强度值。参考试验测得的这2个数据，结合内聚力模型（CZM）和扩展有限元法（X-FEM），在有限元软件A N SY S中分别模拟得到积冰与旋转帽罩之间的界面分离区域和冰形内部裂纹路径及其扩展过程，对旋转帽罩表面积冰甩脱的位置和体积作出预测。预测结果与帽罩表面积冰甩脱试验结果作比较，证明了CZM和X-FEM耦合的数值模拟方法可行。为实际工程应用中的热气或者电防冰系统的布置提供参考。

积冰甩脱；黏附强度；拉伸强度；内聚力模型；扩展有限元法；旋转帽罩；航空发动机

0　引言

当飞机在结冰条件下飞行时，发动机的旋转帽罩会因为大气中过冷水滴的撞击、积聚而结冰。帽罩积冰会影响发动机进气流场，降低气动性能，并且甩脱的积冰可能会打坏风扇叶片甚至压气机部件，影响飞行安全。因此有必要对帽罩积冰在甩脱的具体位置及体积进行预测，为实际工程应用中的热气防冰或电防冰系统的布置提供参考。

积冰/界面黏附强度与很多因素有关，比如基底材料的表面特性、积冰的形成条件、空气温度、冻结速度等。国内外学者采用了多种试验方法测量积冰/金属界面黏附强度［1］，但不同学者提供的结果相差较大。Loughborough［2］发现冰/铜和冰/铝界面黏附强度分别为0.85MPa和1.52MPa；Druez［3］发现冰/铝界面黏附强度在0.075～0.12MPa间随表面粗糙度的增大而增大；Raraty和Tabor［4］试验发现，在-6℃和-15℃条件下，冰/抛光不锈钢界面黏附强度分别为0.03MPa和0.16MPa；丁金波等［5］也通过试验对不同粗糙度金属表面的积冰黏附性能做了研究，黏附强度数值在0.02～0.13MPa之间；李清英等［6］利用电脉冲除冰系统来减小积冰的黏附强度；W.Dong等［7］对旋转帽罩进行热分析，利用热气来减小积冰的黏附强度。

冰内部物理属性也受很多因素的影响，比如环境温度、形成方式、杂质比例等，不同试验测得的冰内拉伸强度差别也很大。Xian和Scavuzzo［8］发现当测试温度从-23.3℃升高到-3.9℃的过程中，积冰拉伸强度从1.172MPa减小到0.827MPa；Reich［9］试验测得霜冰和明冰的拉伸强度不一样，霜冰的拉伸强度是0.12MPa，明冰的拉伸强度为0.62～2.3MPa。

本文利用水杯法分别测量得到积冰/铝板界面黏附强度值和积冰内部拉伸强度值，然后在有限元软件ANSYS中，利用内聚力模型定义冰形与帽罩表面接触单元，模拟得到冰形与旋转帽罩之间的界面分离区域；利用扩展有限元法模拟得到积冰内部裂纹路径及其扩展过程，最终预测旋转帽罩表面积冰甩脱的位置和体积，并与之前学者的试验结果［10］进行比较。

1　试验方法

理论上只有当界面分离和冰内部裂纹同时出现时，旋转帽罩表面的积冰才会发生甩脱，如图1紫色方框部分所示。积冰与帽罩表面界面分离的难易是由积冰/界面黏附强度决定的，而冰内部裂纹形成的难易是由积冰内部拉伸强度决定的。

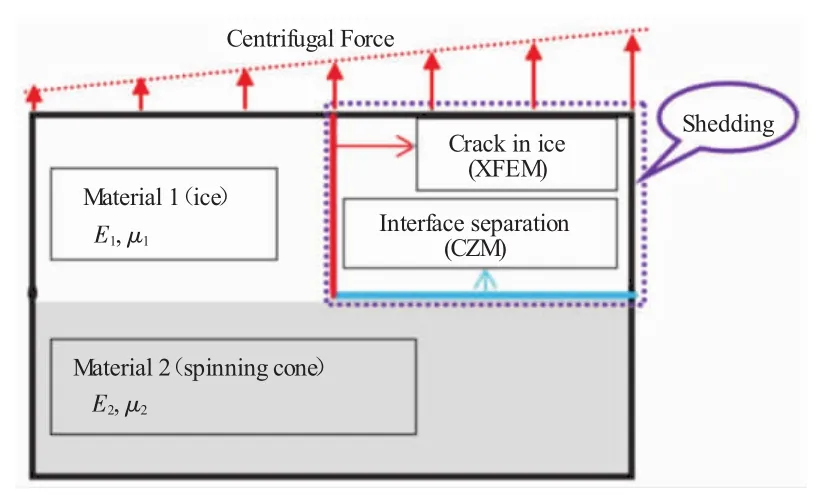
图1　旋转帽罩表面积冰甩脱

1.1积冰/铝板界面黏附强度测试

采用水杯法测量积冰/铝板界面黏附强度如图2所示。其中1为数据采集计算机，内置测试软件为Material Test4.1；2为UTM6104万能拉伸试验机；3为量程为500 N的拉力传感器；4为倒置的水杯，杯口直径为20mm；5为铝板；6为拉伸机固定底座。测量前，先通过水杯底面的小孔给杯中注入3 mL蒸馏水，约占水杯容积的2/3。然后将水杯和铝板整体放入冰柜里，冰柜温度设置为-15℃，冻结24 h后取出，用夹具将铝板固定在拉伸机底座上，水杯端通过1段柔性连接固定在上方夹具上。设置拉伸机向上位移速度参数为5mm/min，最大位移量为20mm，启动拉伸机，直到水杯中冰块与铝板界面完全分离后停止，输出拉力与时间的关系图像，得到过程中最大拉力值Fmax和水杯冰块本身的重力值Gclamp，则界面黏附强度σn为

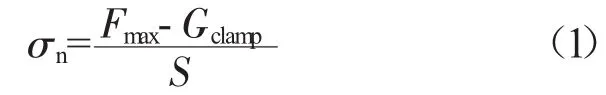
式中：S=3.14×10-4m2，为界面接触面积，即水杯底面积；σn为积冰/铝板界面黏附强度，为了减小试验误差，多次重复试验取平均值，最终算得0.07MPa。

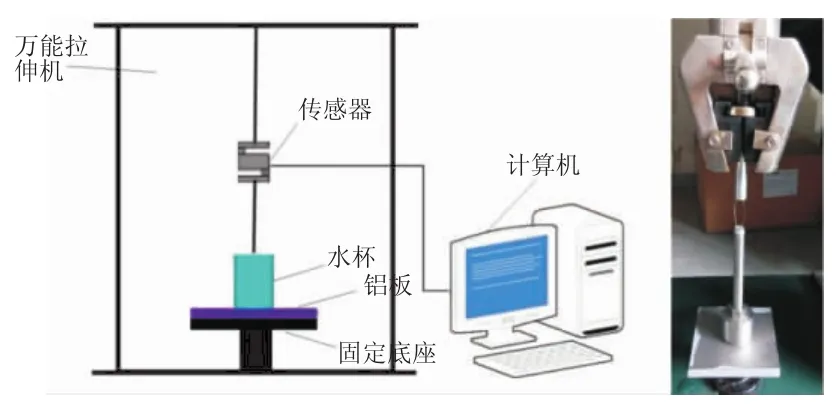
图2　积冰/铝板界面黏附强度测试装置

图3　冰拉伸强度试验装置及结果

1.2积冰内部拉伸强度测试

同样采用水杯法测量积冰内部拉伸强度如图3所示。将2个完全相同的水杯对接好，并注入适量水，放置冰柜中冻结24 h后，2个水杯通过其中的1块整冰牢固地黏在一起，将2个水杯上下固定在拉伸试验机上，拉伸机参数设置与第1.1节的相同，启动拉伸机，直到2个水杯完全分离后停止，输出拉力与时间的关系（图3），得到过程中最大拉伸应力F'max和夹具本身的重力G'clamp，则利用式（1）计算得到积冰内部拉伸强度σt=0.38MPa。

2　数值方法

2.1内聚力模型

内聚力模型是由Alfano和Crisfield［11］首先提出的，Chen Y等［12］利用内聚力模型研究发动机风扇叶片表面积冰的甩脱问题。内聚力模型通过ANSYS软件中的接触单元来实现，如图4所示。OB显示了线弹性加载阶段，BD为线性软化阶段。在B点法向/切向接触应力达到最大值，OB的斜率代表了材料的脆性或黏性。一旦达到材料的开裂强度（B点），其损伤会随循环载荷的增大而累积，而在起裂后的加载/卸载过程中，其斜率与界面损伤程度di有关，界面应力σt与开裂位移δi的关系式为

式中：i=n，t，m，分别对应纯法向型、纯剪切型和混合模式裂纹。界面损伤程度di定义为

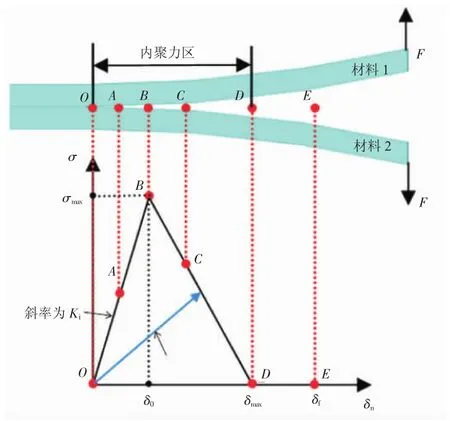
图4　内聚力模型

当△i≤1时di=0，而△i≥1时0＜di≤1，其余参数表示为

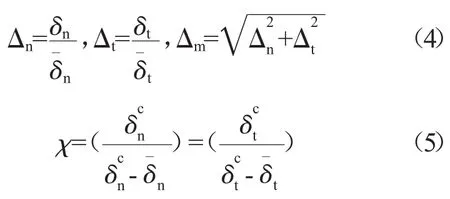
三角形OBD的面积为界面断裂过程中释放的能量即断裂能Gc，一般通过试验获得，其表达式为

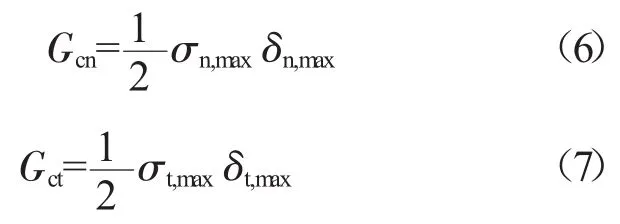
积冰/帽罩界面分离既不是单纯的法向分离，又不是单纯的切向滑移，在这种混合模式下，断裂能满足

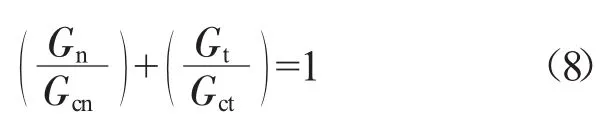
其中

利用ANSYS中的内聚力模型对积冰/帽罩界面破坏区域进行模拟，模拟过程中最重要的2个参数是界面黏附强度σmax和界面断裂能Gc，数值模拟中的断裂能Gc=0.2 N/mm。

2.2扩展有限元法

扩展有限元法由Belytschko和Black［13］首先提出，方修君等［14］利用扩展有限元法对3点弯梁的开裂过程进行了模拟。应用扩展有限元法时，不需要实时地对裂纹尖端区域重新进行网格划分，因为与传统有限元法相比，扩展有限元法修正了有限元的位移函数，改进了对不连续边界的描述方法，使其独立于网格划分，扩展有限元法的位移函数为

传统有限元部分

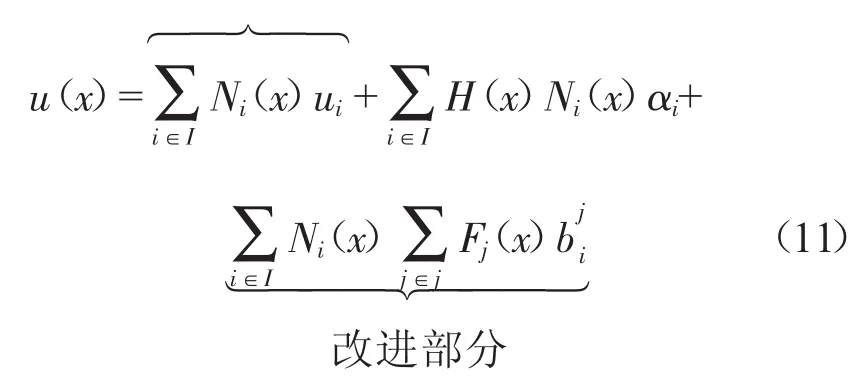
式中：N（ix）为节点i对应的传统有限元法形函数；ui为传统有限元法节点i位移矢量；αi为节点i的扩展自由度变量；F（x）为裂纹尖端弹性渐进函数；j为裂纹尖端节点自由度变量；H（x）为阶跃函数

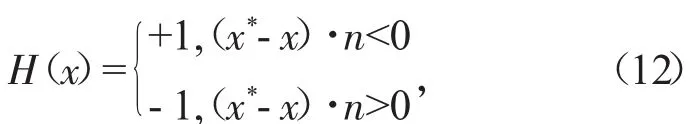
式中：x*为考察点x在裂纹面上的投影点；n为裂纹面的单位外法向。

利用X-FEM模拟冰形内部具体的裂纹路径，设置正确的裂纹初始单元十分重要，所以要先对冰形内部作应力分析，找到最大应力位置，参考试验值，设置极限拉伸强度为0.38MPa。

2.3数值模拟流程

分别利用ANSYS中自带的内聚力模型和扩展有限元方法对积冰/帽罩金属表面的界面分离及积冰内部的裂纹扩展进行模拟，分析流程如图5所示。由于缺少冰风洞等试验条件，帽罩、冰形几何模型的选择与文献［10］的相符。王健等通过试验手段分析旋转帽罩表面冰生长/脱落过程，得到如图6（a）的几何模型，本文利用GetData提取出帽罩及最厚的冰形曲线，在ANSYS里完成几何建模，几何模型中旋转帽罩的锥底直径为100mm，锥角为84°。胡娅萍等［15］发现帽罩锥角的不同对积冰影响很大。积冰的物性参数如下，密度为897kg/m3，弹性模量为9000MPa，泊松比为0.325，拉伸强度设为0.38MPa；帽罩部分的物性参数如下，密度为2700kg/m3，弹性模量70 GPa，泊松比为0.3，积冰在帽罩表面的黏附强度设为0.07MPa。

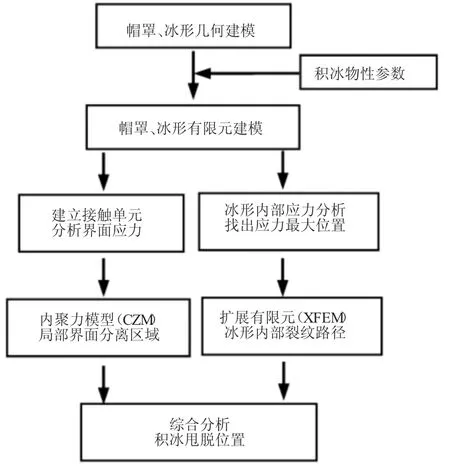
图5　数值模拟分析流程

有限元模型如图6所示。其中图6（b）为帽罩和冰形2维有限元网格，紫色为帽罩部分，有2556个四边形网格，积冰部分有568个四边形网格。模拟过程中进行过网格无关性检验，发现加密网格对结果影响不大。

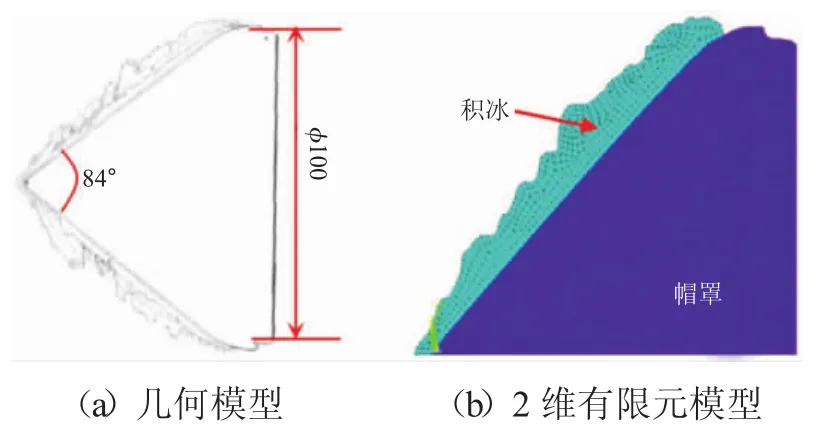
图6　积冰/帽罩几何和有限元模型

3　数值模拟结果分析

3.1界面分离区域

采用ANSYS内置的内聚力模型模拟界面分离区域，因为几何模型的对称性，在冰形和旋转帽罩表面之间建立接触对，采用2维3节点接触单元CONTA172，帽罩表面设为目标面，冰形界面设为接触面，法向和切向刚度均采用默认值，接触类型设为初始接触类型。约束和载荷条件与文献［10］的一致，在帽罩底面所有节点设置轴向约束，帽罩100%转速设为1591.74 rad/s，计算求解。积冰与旋转帽罩接触应力分布如图7所示，根据最大应力强度准则，当界面应力等于0.07MPa时，假设该部分界面发生分离，分离界面如图8红色区域所示。当帽罩转速递增时，损伤系数最大的位置始终不变，距积冰底面17.5mm，如图8所示。

图7　积冰/帽罩界面接触应力分布

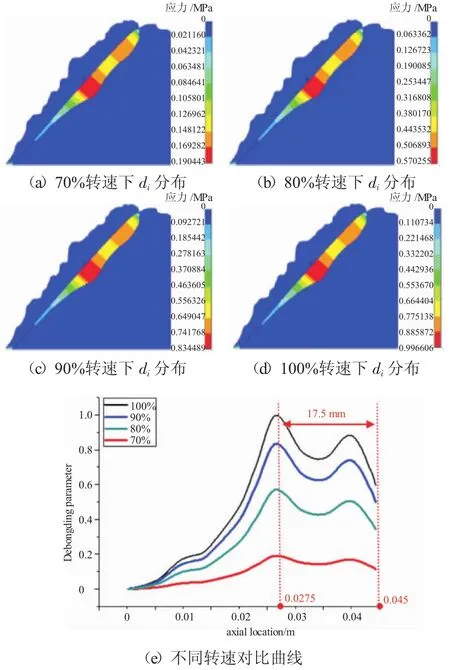
图8　不同转速下界面损伤系数di分布

3.2冰形内部应力

在模拟积冰内裂纹路径之前，要先对积冰作整体应力分析，找到冰形中拉伸应力最大的位置，以便准确设置裂纹初始单元。计算过程中的接触、约束条件、边界条件设置参照第3.1节，积冰在特定转速（70%、80%、90%、100%）下内部拉伸应力分布如图9所示。从图中可见，随着转速的增加，最大应力位置保持不变（恰好距离积冰最底部也是17.5mm，与图8界面损伤系数最大的位置相一致），该位置是冰内最容易发生断裂的位置，应该在该区域设置裂纹初始单元。

图9　不同转速冰形内部拉伸应力分布

3.3冰形内部裂纹扩展

扩展有限元法模拟冰形内部具体的裂纹位置，以最大拉应力理论作为积冰内部断裂准则，极限拉伸强度为0.38MPa。由于冰形周向对称，所以可以将整体冰形简化为2维进行处理，总时间设为1，最小时间步长设为0.0001。裂纹扩展路径如图10所示。从图中可见，裂纹近似平行于轴线方向，裂纹尖端的拉伸应力为0.38MPa，与极限拉伸强度相一致。裂纹扩展过程4个时刻裂纹附近的位移如图11所示，裂纹扩展顺序由a至d。

3.4模拟结果验证

王健等［10］利用高速摄影机拍摄的帽罩旋转过程中积冰甩脱瞬间如图12（a）所示。从图中可见，试验中距离积冰底部5～20mm的区域的积冰发生甩脱。本文积冰甩脱位置的模拟结果如图12（b）所示，其中紫色线框部分是积冰预测甩脱区域，与积冰底部的距离在3～17.5mm之间，积冰甩脱的位置都是在靠近积冰底部的后半段，说明本文采用的内聚力模型和扩展有限元法耦合的数值模拟方法可行。

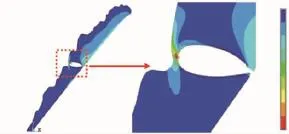
图10　裂纹完全扩展拉伸应力

图11　裂纹扩展过程

图12　试验结果与模拟结果的对比

应力/MPa .189515 42232.3 84464.4 126696 168929 211161 253393 295625 337857 380089

4　结论

本文利用水杯法分别测量积冰/铝板界面黏附强度值σn和积冰内部拉伸强度值σt；并采用数值模拟方法，利用内聚力模型对界面接触单元进行定义，对界面分离区域进行预测，再利用扩展有限元法对积冰内部应力位置进行裂纹初始单元设置，进而有效模拟出积冰内部裂纹扩展路径，最终确定积冰甩脱位置，主要结论如下：

（1）内聚力模型与扩展有限元法的耦合能有效地模拟预测得到帽罩表面积冰甩脱的位置，也为其他部件表面积冰甩脱的分析提供新的思路。

（2）当试验环境温度在-15℃时，由水杯法测得的积冰/铝板界面黏附强度为0.07MPa，积冰内部拉伸强度为0.38MPa。

［1］Javan-Mashmool M，Volat C，Farzaneh M.A new method for measuring ice adhesion strength at anice-substrate interface［J］.Hydrological Processes，2006，20（4）：645-655.

［2］Loughborough D L.Reduction of the adhesion of ice to de-icer surfaces［J］.Journal of the Aeronautical Sciences，2012，13（3）：126-134.

［3］Druez J，Phan C L，Laforte J L.Adhesion of glaze and rime on aluminium electrical conductors［J］.Transactions-Canadian Society for Mechanical Engineering，1978，5（4）：215-220.

［4］Raraty L E，Tabor D.The adhesion and strength properties of ice［J］. Proceedings of the Royal Society a Mathematical Physical&Engineering Sciences，1958（6）：184-201.

［5］丁金波，董威.表面粗糙度对冰冻黏强度影响试验研究［J］.航空发动机，2012，38（4）：42-46. DING Jingbo，DONG Wei.Experimental study of influence of surface roughness on ice adhesion［J］.Aeroengine，2012，38（4）：42-46.（in Chinese）

［6］李清英，朱春玲，白天.电脉冲除冰系统的除冰试验与数值模拟［J］.航空动力学报，2012，27（2）：350-356. LI Qingying，ZHU Chunlin，BAI Tian.De-icing experiment and numerical simulation of the electro-impulse de-icing system［J］.Journal of Aerospace Power，2012，27（2）：350-356.（in Chinese）

［7］Dong W，Zhu J，Zheng M.Thermal analysis and testing of a cone with leading edge hot air anti-icing system［R］.AIAA-2014-0739.

［8］Xian X，Chu M L，Scavuzzo R J，et al.An experimental evaluation of the tensile strength of impact ice［J］.Journal of Materials Science Letters，1978，8（10）：119-130.

［9］Reich A D.Ice property/structure variations across the glaze/rime transition［R］.AIAA-1992-0296.

［10］王健，胡娅萍，吉洪湖，等.旋转整流罩积冰生长与脱落过程的试验［J］.航空动力学报，2014，29（6）：1352-1357. WANG Jian，HU Yaping，JI Honghu，et al.Experiment of ice accrection and shedding on rotating spinner［J］.Journal of Aerospace Power，2014，29（6）：1352-1357.（in Chinese）

［11］Alfano G，Crisfield M A.Finite element interface models for the delamination analysis of laminated composites：mechanical and computational issues［J］.International Journal for Numerical Methods in Engineering，2001，50：1701-1736.

［12］Chen Y，Dong W，Wang Z.Numerical simulation of ice shedding from a fan blade［R］.ASME 2015-GT-42265.

［13］Belytschko T，Black T.Elastic crack growth in finite elements with minimal remeshing［J］.International Journal for Numerical Methods in Engineering，1999，45（5）：601-620.

［14］方修君，金峰，王进廷.基于扩展有限元法的粘聚裂纹模型［J］.清华大学学报，2007，47（3）：344-347. FANG Xiujun，JIN Feng，WANG Jinting.Cohesive crack model based on extended finite element method［J］.Journal of Tsinghua University，2007，47（3）：344-347.（in Chinese）

［15］胡娅萍，吉洪湖，王健，等.锥角对旋转整流罩积冰影响的模拟试验［J］.航空动力学报，2014，29（3）：495-503. HU Yaping，JI Honghu，WANG Jian，et al.Experiment on effect of cone angle on ice accretion of rotating spinner［J］.Journal of Aerospace Power，2014，29（3）：495-503.（in Chinese）

（编辑：栗枢）

Numerical Simulation of Ice Shedding from Spinning Cone

FU Liang，CHEN Yong，WANG An-zheng
（School of Mechanical Engineering，Shanghai Jiaotong University，Shanghai 200240，China）

In order to understand the mechanism and process of ice shedding for spinning cone，the cup method was introduced to measure the ice/Aluminum interfacial adhesive strength and the ice internal tensile strength.The Cohesive Zone Model（CZM）and the eXtended Finite Element Method（X-FEM）were introduced to simulate the ice shedding process from a spinning cone.The CZM was applied to simulate the initiation and propagation of ice/spinning cone interface crack.The X-FEM was introduced to model crack growth inside the ice.The research method provides a reference for ice shedding analysis of other parts of aeroengine.The comparation between simulation and experiment results show that the method is feasible and could also be used to further study optimization of the electrothermal and hot-air deicing system.

ice shedding；interfacial strength；tension strength；Cohesive Zone Model；eXtended Finite Element Method；spinning cone；aeroengine

V 228.8

Adoi：10.13477/j.cnki.aeroengine.2016.05.012

2016-04-30基金项目：国家自然科学基金（51376122）资助

傅亮（1990），男，在读硕士研究生，研究方向为航空发动机结冰力学分析；E-mail：984292889@qq.com。

引用格式：傅亮，陈勇，王安正.旋转帽罩表面积冰甩脱位置的数值模拟［J］.航空发动机，2016，42（5）：70-75FULiang，CHENYong，WANGAnzheng. Numericalsimulationoficesheddingfromspinningcone［J］.Aeroengine，2016，42（5）：70-75.