单自由度系统强迫振动下Kelvin模型和Maxwell模型的比较

王孝然, 　申永军, 　杨绍普

(石家庄铁道大学 机械工程学院，河北 石家庄　050043)



单自由度系统强迫振动下Kelvin模型和Maxwell模型的比较

王孝然, 申永军, 杨绍普

(石家庄铁道大学 机械工程学院，河北 石家庄050043)

以Kelvin模型和Maxwell模型为对象，研究了单自由度系统强迫振动下2种模型的系统响应。首先，将单自由度强迫振动分为简谐激励下的强迫振动、偏心质量引起的强迫振动和支承运动引起的强迫振动3种情况，分别在这3种情况下建立了2种模型的运动微分方程，并得到了系统的解析解。随后，通过解析解得到了振幅放大因子和相位差的解析式，研究了系统的幅频响应曲线和相频响应曲线。通过比较2种模型的幅频响应曲线，发现在偏心质量和支承运动引起的强迫振动情况下Maxwell模型在小阻尼时振动控制效果远优于Kelvin模型。

Kelvin模型；Maxwell模型；强迫振动；幅频响应曲线

0　引言

系统由外界持续激振所引起的振动，称为强迫振动。激励按来源可分为2类，一类是力激励，它可以是直接作用于机械运动部件上的力，也可以是旋转机械或往复运动机械中不平衡量引起的惯性力；另一类是由于支承运动而导致的位移激励、速度激励以及加速度激励[1]。

国内外振动工程教科书中讲述单自由度系统的强迫振动时，多采用Kelvin模型，对Maxwell模型却鲜有人去研究。而工程实践中大量采用粘弹性材料，粘弹性材料不仅具有阻尼性质也具有刚度性质，其力学模型用Maxwell模型表示更合适[2]。Asami等将Maxwell模型引入到动力吸振器中并对其进行了优化设计，发现在相同质量比情况下，该模型具有更好的减振效果[3-4]。文献[5-6]介绍了Maxwell模型在吸振隔振中的应用。文献[7-8]研究了抗蛇形减振器，用Maxwell模型能较准确的作为抗蛇形减振器的简化模型。文献[9]研究了广义的Maxwell模型，提出了一种模型转换的计算方法。文献[10]采用广义Maxwell模型来模拟玻璃模压过程中所表现的粘弹性力学特性。文献[11]研究了用Maxwell模型来近似表示粘弹性阻尼器。文献[12]用Maxwell模型来描述覆盖层材料的力学特性。文献[13]以黏弹性力学理论为基础，选用广义Maxwell模型作为聚碳酸酯黏弹性的力学模型。文献[14]研究了Maxwell模型在完整岩体中的应用。

本文主要讨论单自由度系统的强迫振动，把Kelvin模型和Maxwell模型进行比较，发现偏心质量和支承运动引起的强迫振动情况下，Maxwell模型在小阻尼时振动控制效果远优于Kelvin模型，从而可以为振动系统的设计或修改提供参考依据。

1　简谐激励下的强迫振动

反映系统粘弹性的模型主要有Maxwell模型和Kelvin模型，其本质是弹簧和阻尼器的串联或者并联，如图1所示。3种典型的单自由度振动系统如图2～图4所示，其中图2为简谐激励下系统强迫振动。设x是质量块的位移，x1(t)是串联弹簧和阻尼分割点的位移。kk和ck是Kelvin模型的刚度和阻尼，km和cm是Maxwell模型的刚度和阻尼。质量块上作用有简谐激振力P(t)=P0sinωt，其中，P0为激振力幅，ω为激振频率。根据牛顿第二定律可以得到图2(a)的动力学方程

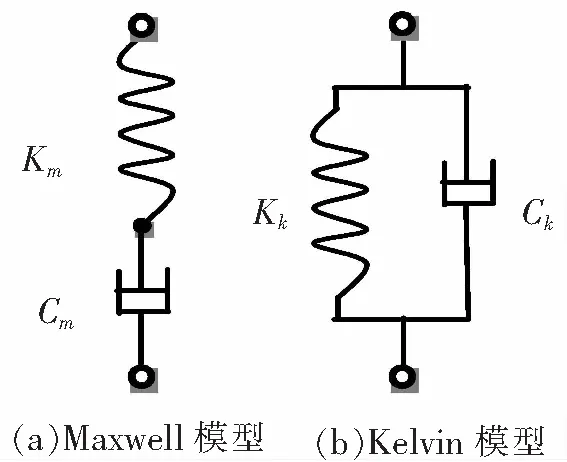
图1　Maxwell模型和Kelvin模型

图2　简谐激励下的强迫振动

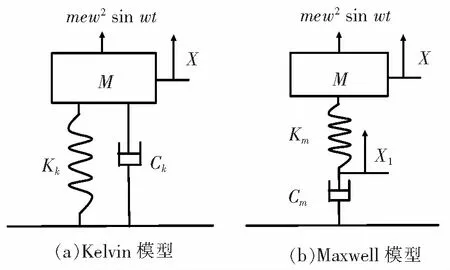
图3　偏心质量引起的强迫振动

图4　支承运动引起的强迫振动

(1)

(2)

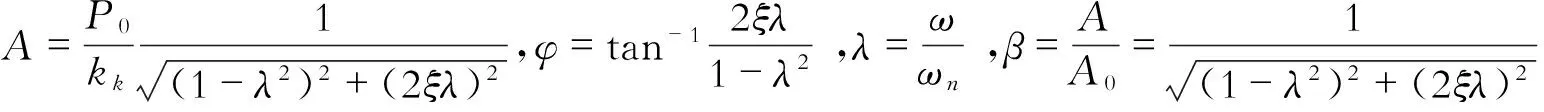
其中,β为无量纲放大因子；A0=P0/kk为质量块在激振力幅静作用下的最大位移。由此可以得到幅频响应曲线和相频响应曲线，如图5和图6所示。

根据牛顿第二定律可以得到图2(b)的动力学方程

(3)

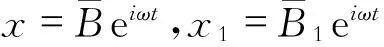
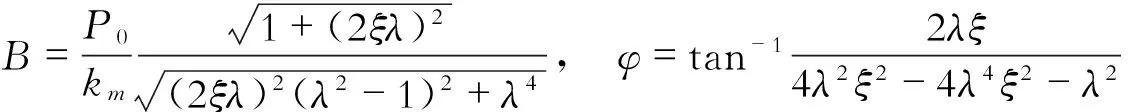
幅频响应曲线和相频响应曲线如图7和图8所示。

图5　幅频响应曲线(简谐激励，Kelvin模型)

图6　相频响应曲线(简谐激励，Kelvin模型)

图7　幅频响应曲线(简谐激励，Maxwell模型)

从Kelvin模型和Maxwell模型的幅频响应曲线可以看到：

(1)当λ≪1，即ω≪ωn时，Kelvin模型的β≈1，说明激振频率相对于系统固有频率ωn很低时，相应的振幅与静位移大小相当；此时Maxwell模型的β趋近于无穷大。当λ≫1，即ω≫ωn时，Kelvin模型和Maxwell模型的β都趋近于0，说明激振频率相对于固有频率很高时，相应的振幅很小，这是因为激振力的方向改变的太快，质量块的位移受惯性的影响来不及有相应的变化。在上述的两个区域内，取不同ξ值时曲线较为密集，说明阻尼的影响并不显著。因此，在这两种极端情况中，系统即使按无阻尼情况考虑也是可以的。

2　偏心质量引起的强迫振动

如图3假设旋转机械的总质量为M，转子的偏心质量为m，偏心距为e，转子的转动角速度是ω。根据牛顿第二定律可以得到图3(a)的动力学方程

(4)

系统的稳态响应为x=Csin(ωt-φ)，其中

写成下列无量纲形式

由此可得到幅频响应曲线和相频响应曲线如图9和图10所示。

图8　相频响应曲线(简谐激励，Maxwell模型)

图9　幅频响应曲线(偏心质量，Kelvin模型)

图10　相频响应曲线(偏心质量，Kelvin模型)

根据牛顿第二定律可以得到图3(b)的动力学方程

(5)

系统的稳态响应为x=Dsin(ωt-φ)，其中

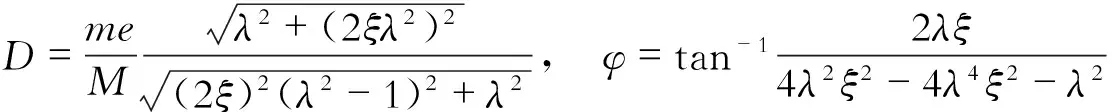
写成下列无量纲形式

可得到幅频响应曲线和相频响应曲线如图11和图12所示。

从Kelvin模型和Maxwell模型的幅频响应曲线可以看到：

(1)当λ≪1，即ω≪ωn时，Kelvin模型和Maxwell模型的振幅都接近于零。当λ≫1，即ω≫ωn时，Kelvin模型和Maxwell模型的振幅都接近于常数me/M，而与激励频率及系统阻尼基本无关。

(3)通过比较可以看出在受偏心质量引起的强迫振动的情况下，Maxwell模型在小阻尼的情况没有出现共振导致振幅过大的现象。

3　支承运动引起的强迫振动

如图4所示假设支承运动的规律是xs=asinωt。根据牛顿第二定律可以得到图4(a)的动力学方程

(6)

把xs=asinωt代入式(6)，得到

(7)

系统的稳态响应为x=Esin(ωt-φ)，从而得到

其中,β为振幅放大因子，可以得到幅频响应曲线和相频响应曲线如图13和图14所示。

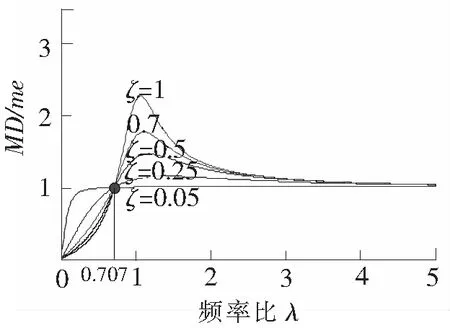
图11　幅频响应曲线(偏心质量，Maxwell模型)

图12　相频响应曲线(偏心质量，Maxwell模型)

图13　幅频响应曲线(支承运动，Kelvin模型)

根据牛顿第二定律可以得到图4(b)的动力学方程

(8)

系统的稳态响应为x=Fsin(ωt-φ)，从而得到

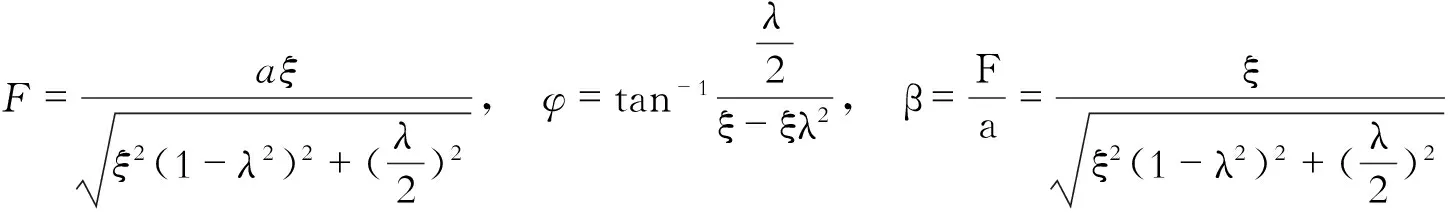
其中,β为振幅放大因，可以得到幅频响应曲线和相频响应曲线如图15和图16所示。

图14　相频响应曲线(支承运动，Kelvin模型)

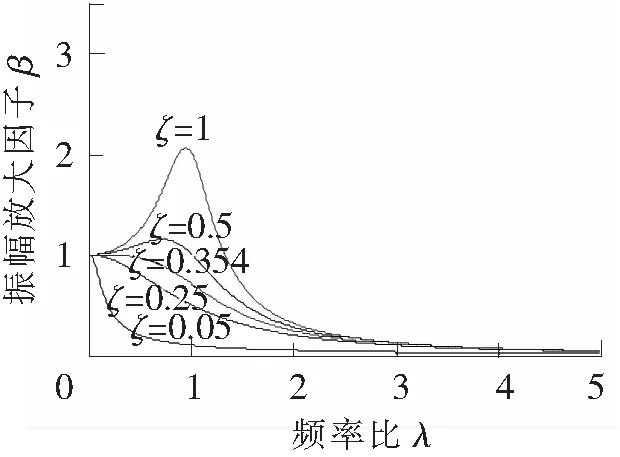
图15　幅频响应曲线(支承运动，Maxwell模型)

图16　相频响应曲线(支承运动，Maxwell模型)

从Kelvin模型和Maxwell模型的幅频响应曲线可以看到：

(1)当λ≪1,即ω≪ωn时，Kelvin模型和Maxwell模型的振幅放大因子β都接近于1。当λ≫1,即ω≫ωn时，Kelvin模型和Maxwell模型的振幅放大因子β都接近于0，而与激励频率及系统阻尼基本上无关。

(3)通过比较可以看出,在受支承运动引起的强迫振动的情况下，Maxwell模型在小阻尼的情况没有出现共振导致振幅过大的现象。

4　结论

本文研究了单自由度系统强迫振动下的Kelvin模型和Maxwell模型，分别求出了2种模型在简谐激励下的强迫振动、偏心质量引起的强迫振动和支承运动引起的强迫振动3种情况下的幅频响应曲线和相频响应曲线。通过比较2种模型的幅频响应曲线发现在偏心质量引起的强迫振动和支承运动引起的强迫振动的情况下，Maxwell模型在小阻尼的情况系统响应远小于Kelvin模型，从而具有较好的振动控制效果。

[1]倪振华. 振动力学[M].西安: 西安交通大学出版社, 1989.

[2]刘耀宗,郁殿龙,赵宏刚,等. 被动式动力吸振技术研究进展[J]. 机械工程学报,2007(3):14-21.

[3]Asami T, Nishihara O. Analytical and experimental evaluation of an air damped dynamic vibration absorber: design optimizations of the three-element type model[J]. Journal of Vibration and Acoustics, 1999, 121(3): 334-342.

[4]Asami T, Nishihara O. H2 optimization of the three-element type dynamic vibration absorbers[J]. Journal of Vibration and Acoustics, 2002, 124(4): 583-592.

[5]徐庆善.动力吸振器的应用动态与进展[J].力学与实践,1992(2):12-15，44.

[6]徐庆善.隔振技术的进展与动态[J]. 机械强度,1994(1):37-42.

[7]张振先,杨东晓,池茂儒. 抗蛇行减振器的模型研究[J]. 机械, 2015(7):1-4，31.

[8]何远,王勇. 抗蛇行减振器串联刚度对高速动车组运行稳定性的影响[J]. 机车电传动,2015(3):26-29.

[9]帅词俊,段吉安,王炯. 关于黏弹性材料的广义Maxwell模型[J]. 力学学报,2006(4):565-569.

[10]张小兵,尹韶辉,朱科军,等. 基于广义Maxwell模型的非球面光学镜片成型模拟[J]. 材料导报,2013(20):148-152.

[11]周圆兀,王囡囡. 设置粘滞阻尼器结构的耗能减震分析[J]. 广西科技大学学报,2015(2):14-19.

[12]卢岩,张荣鹏,林福严,等. 基于三元件Maxwell模型的带式输送机压陷阻力的研究[J]. 矿山机械,2014(3):42-46.

[13]傅志红,喻坚,魏灵娇. 聚碳酸酯的应力松弛实验及数据处理分析[J]. 塑料工业,2014(6):89-92.

[14]王观石,胡世丽,李志文,等. 完整岩体对测井频率应力波的滤波特性[J]. 振动与冲击,2014(23):127-132,154.

A Comparison Study on Kelvin and Maxwell Model for aForced Single Degree-of-freedom System

Wang Xiaoran,Shen Yongjun,Yang Shaopu

(Department of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

Considering the Kelvin and Maxwell model as the research objects, the system responses for the two models are studied based on forced vibration of single degree-of-freedom system. First, the forced vibration is divided into three conditions, such as forced vibration under harmonic excitation, eccentric quality and supporting motion. Under the three conditions, the analytical solutions of the two models are obtained based on the established motion differential equation. Then the analytical formula of amplitude magnification factor and phase difference are obtained, and the amplitude-frequency response curve and phase-frequency response curve are drawn out respectively. By comparing the amplitude-frequency response curves of the two models, it could be concluded that the control performance of Maxwell model is much better than that of the Kelvin model in the case of small damping, which is useful to the design and revision of vibration system.

Kelvin model;Maxwell model;forced vibration;amplitude-frequency response curve

2015-06-28责任编辑:刘宪福DOI:10.13319/j.cnki.sjztddxxbzrb.2016.03.13

国家自然科学基金(11372198)；河北省高等学校创新团队领军人才计划(LJRC018)；河北省高等学校高层次人才科学研究项目(GCC2014053)；河北省高层次人才资助项目(A201401001)

王孝然(1989-),男，硕士研究生，主要研究方向为振动控制。E-mail:wangxiaoranedu@126.com

申永军(1973-)，男，博士，教授，研究方向为机械系统的动力学分析与振动控制。E-mail:shenyongjun@126.com

O328

A

2095-0373(2016)03-0070-06

王孝然, 申永军, 杨绍普.单自由度系统强迫振动下Kelvin模型和Maxwell模型的比较[J].石家庄铁道大学学报:自然科学版,2016,29(3):70-75.